Die Schrödinger-Gleichung für das Wasserstoffatom

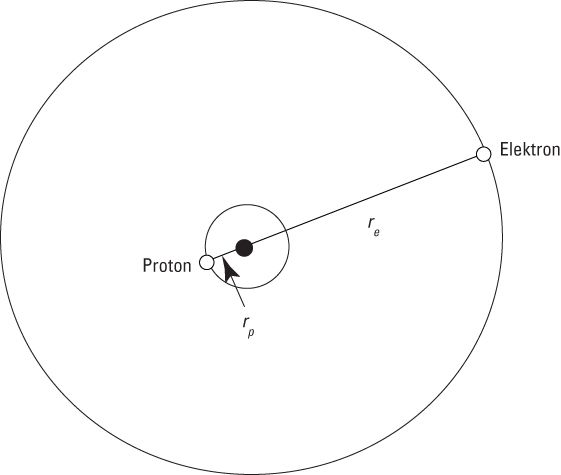
Wasserstoffatome bestehen aus einem einzelnen Proton, um das ein einzelnes Elektron kreist. Abbildung 10.1 zeigt, wie man sich das vorstellen kann.

Beachten Sie, dass sich das Proton nicht genau im Mittelpunkt des Atoms befindet – direkt im Mittelpunkt befindet sich der Schwerpunkt der Massen. Vielmehr ist das Proton auf einer Bahn mit dem Radius r_p zu finden, während sich das Elektron auf einer Bahn mit dem Radius r_e um den Mittelpunkt bewegt.

 

Abbildung 10.1: Das Wasserstoffatom

Wie lautet also die Schrödinger-Gleichung, die die benötigte Wellenfunktionen liefert? Klar, sie enthält Ausdrücke für die kinetische und die potentielle Energie von Proton und Elektron. Für die kinetische Energie des Protons gilt:

wobei gilt. Dabei ist x_p die Position des Protons in x-Richtung, y_p die in y-Richtung und z_p die in z-Richtung.

Die Schrödinger-Gleichung enthält auch einen Ausdruck für die kinetische Energie des Elektrons:

wobei gilt. Dabei ist x_e die Position des Elektrons in x-Richtung, y_e die in y-Richtung und z_e die in z-Richtung.

Neben der kinetischen muss man in der Schrödinger-Gleichung auch die potentielle Energie V(r) berücksichtigen. Somit lautet die zeitunabhängige Schrödinger-Gleichung:

Dabei ist ψ(r_e, r_p) die Wellenfunktion von Elektron und Proton.

Die elektrostatische potentielle Energie V(r) für ein Zentralpotential ist durch folgende Formel gegeben, wobei r der Radiusvektor ist, der die beiden Ladungen trennt:

In der Quantenmechanik ist es üblich, das CGS-System (Zentimeter-Gramm-Sekunde) der Einheiten zu benutzen; hier gilt .

Das von den Ladungen des Elektrons und des Protons verursachte Potential im Wasserstoffatom lautet somit:

Da r = r_e – r_p ist, folgt für die obige Gleichung:

Damit lautet die Schrödinger-Gleichung:

Bevor die Lösung der Schrödinger-Gleichung für das Wasserstoffatom erläutert wird, wird die Gleichung im folgenden Abschnitt zunächst durch die Einführung von Relativ- und Schwerpunkt-Koordinaten vereinfacht.