Ein Gauss'sches Beispiel

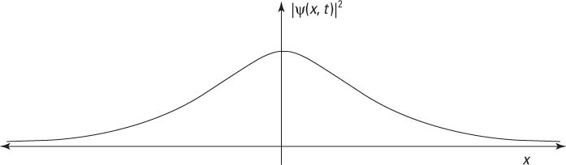
Hier folgt ein Beispiel für die Form eines Wellenpakets. Abbildung 4.12 zeigt ein sogenanntes Gauss'sches Wellenpaket, das an einem Ort lokalisiert und an den anderen null ist.

 

Abbildung 4.12: Ein Gauss'sches Wellenpaket

Man kann folgende Amplitude φ(k) für das Wellenpaket wählen:

Um A zu bestimmen, normalisiert man zunächst φ(k). Das geht wie folgt:

Einsetzen von φ(k) ergibt:

Lösen des Integrals (das meint, in einer mathematischen Formelsammlung nachschlagen) ergibt:

Deshalb ist .

Die Wellenfunktion lautet somit:

Dieses kleine Prachtstück von Integral kann entwickelt werden; man erhält dann:

Das ist also die Wellenfunktion für das Gauss'sche Wellenpaket – und sie ist bereits normalisiert! (Man beachte: Der Teil exp[–x²/a²] ist der Gauss'sche Anteil, der dem Wellenpaket die charakteristische Form gibt, wie sie in Abbildung 4.12 zu erkennen ist.)

Nun kann man dieses Wellenpaket benutzen, um die Wahrscheinlichkeit zu bestimmen, dass das Teilchen sich beispielsweise im Bereich 0 ≤ x ≤ a/2 befindet. Die Wahrscheinlichkeit ist:

In diesem Fall lautet das Integral:

Und das ergibt:

Somit ist die Wahrscheinlichkeit 1/3, dass das Teilchen sich in dem Bereich 0 ≤ x ∞ a/2 befindet. Klasse!