La caja misteriosa
Se han llevado algo. En la esquina del estante hay menos polvo que en el resto. Puede haber sido un libro que estaba tumbado. O una caja.
Holmes en «Peter el Negro».
En muchas de las deducciones que se han mencionado hasta ahora, se parte de la formulación en condiciones ideales de una ley lógica: en el mundo real las cosas no son tan sencillas y no es fácil afirmar que todos y cada uno de los canallas conocidos y por conocer recurrirán al patriotismo en caso de encontrarse en una situación desesperada. Ese es uno de los problemas de la deducción, un método poderosísimo cuando conoces todos los elementos sobre los que aplicar tus reglas, pero no tanto cuando no es así. A continuación ofrezco al lector un sencillo problema lógico, en el que sí conocemos todos los elementos, que nos propone Martin Gardner:
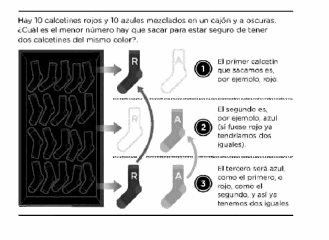
Hay diez calcetines rojos y diez calcetines azules mezclados en el cajón del armario. Los veinte calcetines son exactamente iguales, salvo por el color. El cuarto está absolutamente a oscuras y tú quieres dos calcetines del mismo color. ¿Cuál es el menor número de calcetines que debes sacar del cajón para estar seguro de que tienes un par del mismo color?
¿Podría el lector responder a esa sencilla pregunta antes de continuar leyendo? Piénselo un instante, con la certeza de que en este caso no puede haber duda alguna, puesto que sabemos cuántos elementos hay exactamente en el cajón y cómo es cada uno de esos elementos. ¿Ha dado ya con la solución?
Muchas personas responden que hay que sacar 11 calcetines, otras que es necesario extraer al menos 12. La respuesta correcta, sin embargo, es muy diferente: tan solo necesitamos sacar tres calcetines. El primero será rojo o azul; el segundo, o rojo o azul. Si es del mismo color que el primero, ya hemos resuelto el problema, puesto que tenemos dos calcetines iguales. Pero si el segundo calcetín no es del mismo color, entonces el tercer calcetín tendrá que ser o bien rojo o bien azul: puesto que los dos primeros eran de distinto color, el tercero tendrá que coincidir forzosamente con uno de ellos. Naturalmente, podemos tener la suerte de conseguir dos calcetines iguales sacando solo dos, pero eso dependerá del azar, mientras que con tres es absolutamente seguro, y hay que tener en cuenta que, al menos en el mundo criminal del que se ocupa Holmes, no siempre basta con un conocimiento probable.
El problema de los calcetines muestra que, incluso cuando conocemos todos los elementos en juego, podemos equivocarnos, porque la realidad no se nos presenta de manera tan sencilla como las premisas de un silogismo y existen muchos elementos innecesarios o accesorios (como el número concreto de calcetines rojos y azules en el cajón: diez y diez), que nos pueden confundir y activar no ya nuestro razonamiento deductivo o inductivo, sino el intuitivo. La intuición, como ya hemos tenido ocasión de comprobar, es un arma poderosa, pero a menudo está mal cargada. En este caso, la intuición nos ha sugerido que tenemos que asegurarnos de que se agoten los calcetines de un color, sacando lio incluso 12 calcetines. ¿Por qué? No se sabe, pero es que la intuición es así: nos da una respuesta inmediata y no basada en un razonamiento explícito del que seamos conscientes. Casi siempre acierta, pero en algunas ocasiones muy importantes falla, incluso cuando se trata de Sherlock Holmes: «Yo tengo instinto para estas cosas, pero a veces ese instinto me la juega[280]».
En cuanto a la deducción, hay ejemplos como el de la geometría euclidea que nos muestran que si aceptamos ciertos axiomas, como los cinco postulados de Euclides, a partir de ellos podemos construir todo un mundo de deducciones increíblemente efectivas y exactas. Una vez aceptados los axiomas, todo el conocimiento deducido de ellos es coherente, como decía Holmes, pero, además, los resultados funcionan cuando se aplican a la realidad. Sirven y han servido a lo largo de la historia para construir impresionantes catedrales, arcos increíbles y puentes asombrosos. Al contrario que las premisas de la teología, que nunca nos dejan salir de la abstracción pura, las premisas de las matemáticas nos permiten modificar el mundo en el que vivimos de manera efectiva. Sin embargo, también podemos no aceptar los axiomas de Euclides, por ejemplo el quinto postulado de las paralelas, como hicieron Riemann y Lobachevski en el siglo XIX, y descubrir que la geometría euclidea no es la única posible y que existen otras geometrías, algunas de ellas también aplicables al mundo real, como la elíptica y la hiperbólica.
Ahora bien, imaginemos que, después de sacar un calcetín rojo y uno azul, extraemos un tercer calcetín y resulta ser de color verde. Situaciones como la anterior se pueden explicar al menos de tres maneras: ha sido un descuido de quienes han participado en el experimento, que han introducido en el cajón un calcetín verde sin querer; ha sido un milagro… o ha sido un truco. El descuido nos lleva a considerar lo importante que es la elección de las premisas, el rigor científico y la necesidad de controles cada vez más sofisticados; el milagro nos conduce a la religión o a una nueva metafísica; el truco, a un salón de magia o a los parajes de la seudociencia, a las manos de un mago o a las de un farsante, a los dominios de Uri Geller y el Conan Doyle espiritista o a los de Houdini y Sherlock Holmes, quien dijo: «Debemos buscar la coherencia; allí donde falta la coherencia, hemos de sospechar que hay engaño[281]».