EL CISNE NEGRO DE TALEB Y LOS MUNDOS SUJETOS A LA AMENAZA DE UN PELIGROSO COLETAZO

EL CISNE NEGRO DE TALEB Y LOS MUNDOS SUJETOS A LA AMENAZA DE UN PELIGROSO COLETAZO

Una de las muletillas más habituales que se oyeron al empezar a notarse los efectos de la crisis fue la de que nadie habría podido preverla. Aquello había sido una especie de equivalente financiero del meteorito que había borrado de la faz de la Tierra a los dinosaurios. Todas las estrategias de diversificación y cobertura presuntamente dotadas de la capacidad de evitar que los bancos se volatilizaran quedaron inutilizadas al verse cogidas por sorpresa las entidades —por emplear las palabras de David Viniar, director financiero de Goldman Sachs— a causa de una cortina de humo formada por «una batería de movimientos equivalentes a veinticinco veces la desviación estándar y sostenidas por espacio de varios días seguidos».^[60] Esto guarda cierta semejanza con la afirmación relativa al «acontecimiento de diez sigmas» que según se dice vino a invocar John William Meriwether al asistir al estallido de su fondo de cobertura —denominado Long Term Capital Management— en 1998.^[61]

Lo que estos sigmas pretenden señalar es el número de desviaciones estándares que es preciso apartarse del valor medio de una distribución estadística para que se produzca, siempre en términos probabilísticos, un determinado resultado, dándose la circunstancia de que cada nuevo grado sigma (o incremento de su número) tiene cada vez menos probabilidades de verificarse que el anterior. De acuerdo con el señor Viniar, lo que sucedió en 2008 fue algo «comparable a ganar veintiuna o veintidós veces seguidas el gordo de la lotería».^[62] De manera similar, el acontecimiento de diez sigmas del que habría sido víctima en 1998 el Long Term Capital Management, un fondo de inversión libre de carácter especulativo, vendría a constituir un suceso cuya probabilidad de ocurrencia era más o menos de unas tres veces en todo el período de vida del universo. El hecho de que ambos acontecimientos se produjeran con una diferencia temporal que apenas llega a los nueve años muestra claramente que este tipo de afirmaciones son absurdas. Y también acierta a señalar por qué las ideas de la gestión del riesgo y de la ingeniería financiera resultan tan tremendamente problemáticas a los ojos de Nassim Nicholas Taleb.

Es muy habitual que las afirmaciones relacionadas con los sigmas aludan a una distribución probabilística de carácter «normal» o «gaussiano». La forma de la distribución reviste una notable importancia. Si su forma es «normal» quiere decir que se ajusta a lo que se llama una «distribución de Gauss», cuya silueta es la de la clásica curva acampanada y que se caracteriza por el hecho de que la mayor parte de los sucesos medidos por el análisis estadístico se concentran en el centro de la distribución, con un número de acontecimientos que decrece tanto más cuanto más nos alejemos del centro hacia los dos extremos o colas de la gráfica (véase la figura 2.1).

Para comprender dónde radica la importancia de todo esto es preciso imaginar que hemos estudiado una muestra cuyos datos consisten en una colección de valores formada por la estatura de diez mil adultos seleccionados al azar. Descubriremos que la talla de la mayoría de esas personas se sitúa entre un 1,52 y 1,82 metros, que es muy escaso el número de individuos que presenta una estatura superior a los 2,10 metros o inferior a los 91 centímetros, y que no hay un solo caso en nuestra muestra que se salga del rango de valores considerado. Sabiendo esto, podremos estimar las probabilidades de que una persona elegida aleatoriamente y de cualquier estatura se encuentre próxima a la media de dicha distribución. En una distribución de carácter normal, la existencia de una desviación de un sigma implica que la probabilidad de que la estatura de esa persona en cuestión se halle cerca de la media es del 68 por 100.

Figura 2.1: Distribución «normal» de un conjunto de acontecimientos probables

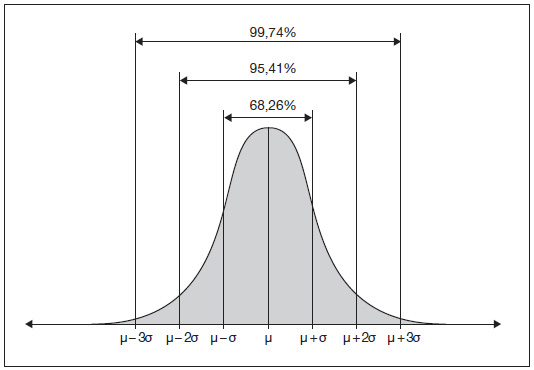
La presencia de una desviación de dos sigmas implica que existe un 95 por 100 de probabilidades de que el individuo en cuestión se sitúe en las proximidades de la media, etcétera; hasta llegar a las colas de la gráfica, que son extremadamente finas debido a que suponen que nadie alcanza jamás una estatura superior a los 2,40 metros. A medida que los números sigma crecen, la probabilidad de encontrar a alguien de la desmesurada estatura que estos vienen a implicar decrece de forma exponencial. Las probabilidades de que alguien venga a caer totalmente fuera del rango muestral considerado terminan siendo tan escasas que básicamente pueden descartarse.

Bastará con cambiar ahora la variable, sustituyendo el valor «estatura» por el de «probabilidades de impago», para comprender por qué esta forma de concebir la probabilidad de uno o más acontecimientos futuros puede resultar de enorme utilidad para los bancos en su intento de ajustar los riesgos de sus carteras de valores y de su exposición en bolsa. El tipo de medición técnica que permitió a los bancos obtener esta información se conoce con el nombre de «análisis de Valor en Riesgo» (o VaR, según sus siglas inglesas «Value at Risk»), cuya fórmula es parte integrante de un más amplio conjunto de modelos matemáticos diseñados para ayudar a los bancos a gestionar el riesgo. Lo que acostumbra a hacer un análisis de Valor en Riesgo es generar una cifra (es decir, un número de Valor en Riesgo) que indica el montante de lo que una determinada empresa puede ganar o perder de embarcarse en una operación específica. Procediendo a la suma de los números de Valor en Riesgo se puede obtener una estimación de la exposición global al riesgo que está asumiendo una compañía dada. Pensemos ahora en el siguiente ejemplo.

¿Qué es lo peor que podría haberle sucedido al mercado inmobiliario estadounidense en 2008? Como ya hemos visto en el ejemplo de las estaturas, la respuesta depende de la muestra de datos elegida para calibrar el modelo. Antes de 2007, el peor revés del que tenían datos las empresas era el de los efectos de la morosidad hipotecaria registrada en Texas en la década de 1980, un suceso que había provocado que las viviendas perdieran el 40 por 100 de su valor. Si tomamos esos datos como límite paramétrico, esto es, como medida de lo mucho o lo poco que debe alejarse del centro la cola de la campana de la distribución antes de que los valores de sigma empiecen a ser demasiado elevados como para poder siquiera imaginar que ocurran, llegaremos a la conclusión, suponiendo que la distribución de los acontecimientos se ajuste al modelo normal de Gauss, de que la probabilidad de que todas las hipotecas de nuestra cartera experimenten simultáneamente una pérdida superior al 40 por 100 de su valor es ridículamente pequeña. Tan pequeña de hecho que puede uno desentenderse de ella. Y en realidad así es: la probabilidad de que todas las obligaciones hipotecarias tengan un bajón o de que un gran banco vaya a la quiebra es absurdamente pequeña, del orden de diez sigmas o más —vuelve a salir aquí ese guarismo mágico—, siempre que uno piense que la distribución probabilística que tiene uno delante obedece a la distribución normal de Gauss. De este modo, una vez calculado, el número de Valor en Riesgo vendrá a reflejar esta circunstancia.

Nassim Nicholas Taleb nunca creyó que esta línea de razonamiento fuese acertada. Ya en 1997 había criticado los modelos de Valor en Riesgo, argumentando que venían a subestimar de forma sistemática la probabilidad de los acontecimientos de gran impacto y baja probabilidad. También había explicado que la parte fina de las colas de la curva gaussiana funcionaban en el caso de las estaturas de la gente, pero no en el de las variables financieras, cuyas colas eran «gruesas». Las probabilidades que se asocian con la presencia de colas gruesas no decrecen de manera exponencial, con lo que la ocurrencia de acontecimientos excepcionales, esto es, situados más allá de los límites significativos de la gráfica, es mucho más frecuente que los modelos que manejaban los bancos les permitían imaginar. Esta es la razón de que se produjeran efectivamente dos acontecimientos de diez sigmas con tan sólo nueve años de diferencia.

El libro que Taleb publicó en 2006, antes de que estallara la crisis, titulado El cisne negro. El impacto de lo altamente improbable,^[*] transformaría estas críticas del Valor en Riesgo en un ataque en toda regla contra la forma en que tanto bancos como gobiernos habían enfocado la crisis. Lo que venía a hacer Taleb en ese libro era básicamente plantear una pregunta: ¿qué sucedería si se topara uno con una persona de 2,60 metros de estatura tras haber evaluado una muestra formada por diez mil personas de talla inferior? Es muy posible que dijéramos con gran aplomo, dado que nunca hemos encontrado a nadie de semejantes características, que no existen seres humanos de esa estatura. Dar con alguien, hombre o mujer, de esa talla, sería un acontecimiento de diez sigmas. Sin embargo, Taleb apostaría contra nuestra convicción, y perderíamos, puesto que en el mundo de las finanzas no hay manera de saber si va uno a acabar dándose o no de bruces con el equivalente de una persona de 2,60 metros de estatura.

El elemento clave en este caso es la cuestión de la experiencia observacional. Si uno no ha tenido la posibilidad de vivir durante un lapso de tiempo igual a la tercera parte de la edad del universo (para poder asistir a un acontecimiento de diez sigmas), ¿cómo puede pretender uno entonces saber qué es lo que puede darse o no darse en un período de semejante magnitud? Lo que nos dice qué es posible o no es la distribución supuesta, no nuestra experiencia. Por volver al ejemplo de las estaturas, hay que señalar que el simple hecho de que nuestro modelo estime que no existen personas de dos metros y sesenta centímetros de estatura no implica que no haya de hecho alguien de esa talla y que no sea factible topar un día con una mujer de tales dimensiones. El ejemplo que pone Taleb es el de los cisnes, que eran todos de color blanco hasta que los europeos llegaron a Australia y descubrieron la existencia de cisnes negros. El exhaustivo muestreo realizado por los europeos a lo largo de muchos años y en múltiples lugares y por el que se había pasado revista a la totalidad de los cisnes conocidos había convencido a los europeos de que todas las aves de esa clase eran blancas —hasta que toparon con unas que no lo eran—. No había nada en la muestra que habían evaluado hasta ese momento, por muy completa que pudiera ser, que alcanzara a indicarles que un día iba a volar hasta ellos un cisne negro. ¿Cómo es posible entonces protegerse frente a la ocasional ocurrencia de riesgos que no aparezcan contemplados en la muestra que manejamos? ¿Cómo va uno a conocer lo incognoscible antes de que se revele? La respuesta es, fundamentalmente, que resulta imposible hacerlo, y en caso de que dé uno en pensar que no lo es estará sentando las bases de su propia perdición.