7.3. Elementhäufigkeitsanalysen von Sternen

Ziel der Stellaren Archäologie ist es, die detaillierten Elementhäufigkeitsmuster der metallärmsten Sterne zu bestimmen. Hinter dem etwas sperrigen Begriff Elementhäufigkeitsanalyse verbirgt sich das Verfahren, das uns verrät, wie die äußeren Gasschichten eines Sterns quantitativ zusammengesetzt sind. So gelingt es, metallarme Sterne als solche zu identifizieren und mehr über das junge Universum und die damaligen Nukleosyntheseprozesse in ihm zu erfahren.

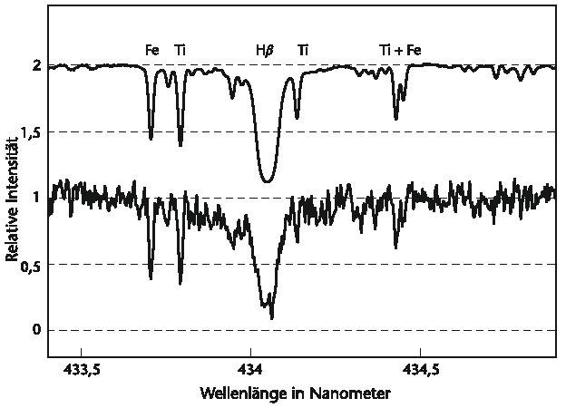
Für eine vollständige Häufigkeitsanalyse benötigt man zunächst ein hochaufgelöstes Spektrum des betreffenden Sterns. Das ist einfacher gesagt als getan: Meist ist der Stern lichtschwach, und man braucht große Teleskope und lange Belichtungszeiten, bis sich das gewünschte Spektrum (Signal) ausreichend deutlich gegenüber allen Störungen, etwa dem Rauschen der aufnehmenden Kamera, abzeichnet. Abbildung 7.5 zeigt Spektren eines Sterns mit verschiedenen Signal-Rausch-Verhältnissen und den entsprechenden Beobachtungszeiten. Daran lässt sich sofort erkennen, dass längere Belichtungen zu besserer Datenqualität mit einem höheren Signal-Rausch-Verhältnis führen. Leider steigt das Signal-Rausch-Verhältnis nur mit der Wurzel der Beobachtungszeit an: Für ein doppelt so gutes Signal-Rausch-Verhältnis muss die Beobachtungszeit viermal so lang sein. Besonders bei schwächeren Sternen führt diese Tatsache oft dazu, dass die Spektren eher »verrauscht« sind.

Abb. 7.5: Normalisierte Spektren eines Sterns mit verschiedenen Signal-Rausch-Verhältnissen (S/N) im Bereich der Hβ-Linie. Oben: Spektrum mit hohem S/N von ~ 300. Unten: Spektrum mit S/N von ~ 13. Um das hohe S/N zu erhalten, müsste der schwächere Stern etwa 530 Mal länger beobachtet werden oder sieben Magnituden heller sein. Das obere Spektrum ist versetzt.

Wie kann nun die chemische Zusammensetzung eines Sterns mit Hilfe seines Spektrums bestimmt werden? Die Hauptarbeit einer Analyse basiert auf der Vermessung der Absorptionslinien im beobachteten Spektrum. Dabei wird die Stärke der Linien bestimmt, was mathematisch gesehen der Fläche der Linienkurve entspricht. Die Stärke einer Linie ist ein Maß dafür, in welchen Mengen das jeweilige Element in der Sternatmosphäre vorkommt. Bevor man nun die Linien im Spektrum mit verschiedenen Computerprogrammen vermessen kann, muss man allerdings erst einmal wissen, welche Linien zu welchen Elementen gehören. Dank der umfangreich katalogisierten atomphysikalischen Eigenschaften jedes Elements kann man genaue Angaben zu den Wellenlängen und weiteren Details der einzelnen Spektrallinien eines jeden Elements nachschlagen. Dadurch ist es relativ einfach, die Linien im Sternspektrum zu identifizieren. Wenn man dann Linien eines bestimmten chemischen Elements im Spektrum eines Sterns gefunden hat, ist das der Beweis dafür, dass dieses Element tatsächlich in der Sternatmosphäre vorkommt. Mit Hilfe eines Sternatmosphärenmodells können diese Linienmessungen dann später in Häufigkeitsangaben umgewandelt werden.

In der Praxis wird allerdings oft der umgekehrte Weg eingeschlagen. Wir wissen, bei welchen Wellenlängen sich wichtige Spektrallinien befinden, und so suchen wir gezielt nach diesen bestimmten Linien, um sie dann zu vermessen. So wird jedes neue Spektrum noch am Teleskop z.B. auf die Neutroneneinfangelemente Strontium, Barium und Europium hin untersucht. Strontium hat seine stärkste Linie bei 4077 Ångström, Barium bei 4554 Ångström und Europium bei 4129 Ångström. Die meisten metallarmen Sterne zeigen nur Rauschen an der Stelle, wo die Europiumlinie sein soll. Die Präsenz einer starken Europiumlinie bedeutet deswegen, dass der Stern sehr wahrscheinlich ein r-Prozess-Stern oder anderweitig interessant ist. Aber auch besonders starke oder nicht existente Strontium- und Bariumlinien deuten auf eine unter Umständen sehr interessante nukleosynthetische Herkunft des Sterns hin.

Ångström? Lichtwellenlängen sollten in der Physik der Konvention nach in Nanometern (nm) angegeben werden. In guter historischer Tradition verwenden Astronomen für die Wellenlängen der Spektrallinien aber immer noch die Einheit »Ångström« (abgekürzt Å). Zehn Ångström entsprechen einem Nanometer. Astronomen scheinen Kommastellen nicht besonders zu mögen. Die Verwendung der Einheit Ångström vermeidet sehr kleine Zahlen oder zu viele Kommastellen, die beim Gebrauch von Nanometern unvermeidbar wären. So hat z.B. die wichtige Uranlinie (siehe Kapitel 5.3 und auch Abbildung 5.8) auf der Ångström-Skala eine Wellenlänge von 3859,57 Å, was 385,957 nm entspricht.

Der Unterschied in der Schreibweise mag eher trivial erscheinen – aber dennoch ist die Ångström-Schreibweise hier hilfreich, denn die schwache Uranlinie befindet sich zwischen drei weiteren Linien. Bei den »Nachbar«-Linien handelt es sich um eine Eisenlinie bei 3859,21 Å und eine Neodyniumlinie bei 3859,43 Å auf der linken, kurzwelligeren Seite der Uranlinie sowie eine starke Eisenlinie bei 3859,91 Å auf der anderen Seite. Die Wellenlängen unterscheiden sich lediglich in den Kommastellen, da sie so nah beieinanderliegen und sich teilweise überlappen. In der Nanometer-Schreibweise würden sich die Wellenlängen erst in der zweiten Kommastelle unterscheiden, und auch die dritte Kommastelle wäre noch sehr wichtig, um die genaue Position einer Linie zu beschreiben.

Ein weiterer Vorteil der Verwendung von Ångström wird bei der Vermessung der Absorptionslinien deutlich. Die schwächsten von ihnen sind oft nur wenige Milli-Ångström breit, während die stärkeren bis hin zu 200 Milli-Ångström zeigen. Beispiele für verschiedene Absorptionslinien können in Abbildung 7.5 gesehen werden. Einige Linien wie die Balmerlinien sind noch viel stärker, aber aus sternatmosphärentechnischen Gründen für eine detaillierte Häufigkeitsbestimmung unbrauchbar. In Nanometern würden die Linienstärken von 0,001 nm bis 0,02 nm reichen. Die unkonventionelle Längeneinheit Ångström ist in der Spektroskopie also einfach praktischer als die SI-Einheit nm.

Eisen hat im Gegensatz zu anderen Elementen den Vorteil, dass es ein sehr reichhaltiges Absorptionslinienspektrum besitzt. Das bedeutet, dass im gesamten visuellen Spektralbereich zahlreiche Eisenlinien zu finden sind. Bei metallreicheren Sternen sind es Tausende von Linien, während bei metallärmeren Sternen nur noch mehrere hundert übrig bleiben. Bei besonders metallarmen wärmeren Sternen sind nur noch eine Handvoll Eisenlinien im Spektrum sichtbar. Aus verschiedenen Gründen können nicht alle Linien vermessen werden, schon gar nicht in metallreichen Sternen, da sich die vielen Linien dann alle überlappen. Aber dennoch ist Eisen das Element, für welches bei weitem die meisten Linienmessungen vorgenommen werden können. Die große Anzahl der Linien erleichtert die Bestimmung der Stern-Metallizität ungemein, da man für die Messung nicht auf einen bestimmten Spektralbereich angewiesen ist. Weiterhin haben diese vielen Einzelmessungen zur Folge, dass der Gesamtfehler der Eisenhäufigkeit meist sehr niedrig ist.

Dies ist enorm wichtig, denn mit wenigen Ausnahmen beschreibt die Eisenhäufigkeit eines Sterns seine gesamte Metallhäufigkeit – also die Häufigkeit aller Elemente außer Wasserstoff, Helium und Lithium. Eisen dient aus diesem Grund auch als Referenzelement für alle weiteren Häufigkeitsverhältnisse. Astronomen lieben es, Häufigkeitsverhältnisse zu berechnen, statt absolute Einzelhäufigkeiten zu verwenden, denn Häufigkeitsverhältnisse haben u.a. den großen Vorteil, dass sich verschiedene systematische Messunsicherheiten größtenteils gegenseitig aufheben.

Aber wie häufig kommt Eisen, etwa im Verhältnis zu Wasserstoff oder anderen Elementen, vor? In den Spektren metallarmer Sterne können in der Regel Absorptionslinien von etwa 15 bis 20 Elementen identifiziert und vermessen werden. Dies beinhaltet Linien von den CNO-Elementen, α-Elementen und Eisengruppenelementen (siehe auch Tab. 3.2). Weiterhin sind die Neutroneneinfang-Elemente Strontium und Barium in den meisten metallarmen Sternen vertreten, solange die Oberflächentemperatur nicht zu warm ist, so dass die Linienstärken deswegen zu schwach für eine Detektion werden. Schließlich werden dann die Häufigkeitsverhältnisse wie C:Fe, O:Fe, Mg:Fe und so weiter gebildet. In einigen Fällen sind auch Verhältnisse wie C:O oder Sr:Ba hilfreich, um bestimmte Nukleosynthesevorhersagen zu testen.

Wie erhält man denn nun die Werte für die Elementhäufigkeiten aus den Messungen der Linienstärken? Dafür benötigt man aufwendige Computerprogramme, die die Sternatmosphäre simulieren. Bei diesen Modellrechnungen werden die äußeren Schichten eines Sterns nachempfunden und die darin ablaufenden physikalischen Prozesse berechnet, die zur Absorption im Spektrum des simulierten Sterns führen. Wenn ein neuer Stern analysiert wird, braucht man also eine Modellatmosphäre, die genau zu diesem Stern passt und seine Eigenschaften gut beschreibt.

Sternatmosphären unterscheiden sich hauptsächlich in den Parametern Temperatur, Schwerebeschleunigung und chemische Zusammensetzung. In der Atmosphäre eines Riesensterns herrscht z.B. eine geringere Schwerebeschleunigung, also ein geringerer Druck als in einem Hauptreihenstern – diese Unterschiede müssen berücksichtigt werden. Also müssen die stellaren Parameter, die Oberflächentemperatur, die Schwerebeschleunigung an der Oberfläche und die Metallizität des Sterns für die Modellatmosphäre bestimmt werden. Dass die Temperatur grundlegend für die Elementhäufigkeitsbestimmung ist, wurde schon angedeutet: Denn die Linienstärken im Spektrum hängen nicht nur von der chemischen Zusammensetzung ab, sondern auch von der Oberflächentemperatur des Sterns. Benutzt man bei dem Modell eine falsche Temperatur, verfälschen sich dadurch die Häufigkeiten. Das Gleiche gilt für die Schwerebeschleunigung, die an der Oberfläche herrscht.

Mit etwas Erfahrung kann man einem Spektrum schon ansehen, ob es sich bei dem Stern um einen Riesen- oder einen Hauptreihenstern handelt. Die genaue Oberflächentemperatur kann so aber nicht bestimmt werden. Stattdessen kann man die Oberflächentemperatur entweder mit Hilfe der gemessenen Sternhelligkeit durch verschiedene Temperaturkalibrationen bestimmen oder von der Tatsache Gebrauch machen, dass die Häufigkeiten aller Eisenlinien, als Funktion ihrer Anregungspotentiale alle gleich sein müssen. Sonst würden verschiedene Linien sehr verschiedene Eisenhäufigkeiten liefern, obwohl der Stern ja nur eine einzige Eisenhäufigkeit besitzt. Ein ähnliches Argument wird bei der Bestimmung der Schwerebeschleunigung verwendet. Die Stärke der Absorptionslinien von einfach ionisiertem Eisen ist von der Schwerebeschleunigung abhängig, die der neutralen Eisenlinien aber nicht. Sowohl die Linien von neutralen wie auch ionisierten Eisenatomen müssen aber die gleiche Eisenhäufigkeit, die des Sterns, liefern. So kann die richtige Schwerebeschleunigung gefunden werden.

Diese Prozedur ist ein gewisses Puzzlespiel. Aber nach einigen Durchgängen und Versuchen kommt man ans Ziel und hat dann bestimmt, welche Temperatur, Schwerebeschleunigung und letztendlich auch Metallizität ein Stern hat. Mit den richtigen Parametern passt die Modellatmosphäre schließlich zum beobachteten Stern. Dann können endlich die individuellen Häufigkeiten aller Elemente berechnet werden, deren Linien im Spektrum vermessen wurden.

In der Praxis wird dieses Verfahren der Elementhäufigkeitsbestimmung auch in umgekehrter Reihenfolge ausgeführt. Viele Linien im Spektrum überlappen sich und formen komplizierte Absorptionsgebilde. Möchte man die Häufigkeit eines Elements aus einer solchen überlappenden Linie ermitteln, muss dies auf andere Weise als mit der direkten Linienvermessungstechnik erfolgen. Aus der vorhergehenden Analyse der Linienstärken ist schon bekannt, welche Modellatmosphäre den Stern am besten beschreibt. Diese Tatsache kann man sich hier zunutze machen: Wir können das Modell verwenden, um ein synthetisches Spektrum zu erzeugen. Die verschiedenen Elementhäufigkeiten können dabei in der Modellatmosphäre variiert werden. Damit »bastelt« man eine komplizierte Absorptionsregion im Spektrum nach. Einzig und allein die verschiedenen Häufigkeiten der beteiligten Elemente bestimmen nun die Stärke der Linien, die sich überlappen. Abbildung 7.5 und auch Abbildung 5.8 zeigen eine solche spektrale Region zusammen mit einem synthetisierten Spektrum, welches das beobachtete Spektrum gut wiedergibt. So können die individuellen Häufigkeiten der beteiligten Elemente trotz Überlappungen der Linien bestimmt werden.

Letztendlich beschreiben alle gemessenen Häufigkeiten die Anzahl der Atome eines Elements in der Sternatmosphäre im Verhältnis zur Anzahl der Wasserstoffatome. Als praktisches Kürzel hat sich für das Häufigkeitsverhältnis zweier Elemente A und B eine Klammernotation eingebürgert: [A/B]. Die Klammernotation drückt zudem aus, dass die Häufigkeit relativ zur Sonne bestimmt wurde. Mathematisch gesehen kann ein solches Verhältnis mit

[A/B] = log₁₀ (N_A/N_B)_Stern – log₁₀(N_A/N_B)_Sonne

ausgedrückt werden. Das sieht auf den ersten Blick kompliziert aus, drückt aber nichts anderes aus als das logarithmische Verhältnis der Anzahl N der Atome eines Elements A geteilt durch die des Elements B in der Atmosphäre des Sterns im Vergleich zur Sonne.

Betrachten wir dazu ein paar Beispiele, die veranschaulichen, dass diese Schreibweise sehr praktisch und einfach zu verstehen ist. Die Eisenhäufigkeit wird ja als Indikator für die Metallizität des Sterns herangezogen. In diesen Fällen wird also das Verhältnis von Eisen zu Wasserstoff ermittelt und dann mit dem solaren Wert verglichen. Die zugehörige Klammernotation sieht so aus: [Fe/H]. Einem Stern, der das gleiche Verhältnis von Eisen zu Wasserstoff wie die Sonne aufweist, wird eine Metallizität von [Fe/H] = 0 zugeordnet. Sonnenähnliche metallreiche Sterne haben dementsprechend [Fe/H] ~ 0.

Enthält ein Stern doppelt so viele Eisenatome pro Wasserstoffatom wie die Sonne, beträgt seine Metallizität [Fe/H] = 0,3 (nicht 2, weil die Notation logarithmisch ist). Wenn umgekehrt die Metallizität unter 0 liegt, enthält der Stern weniger Metallatome als die Sonne und gilt somit grundsätzlich als metallarm. Ein Stern mit [Fe/H] = –1 hat dann nur noch zehnmal weniger Eisenatome als die Sonne. Extrem metallarme Sterne haben [Fe/H] = –3 oder weniger. Tabelle 3.1 enthält diese Informationen schon indirekt, denn –3 als logarithmischer Wert bedeutet 1/1000stel des solaren Eisenwertes. Sterne mit [Fe/H] = –5 haben somit nur ein 1/100 000stel des solaren Eisenwertes. Insgesamt haben Astronomen mittlerweile [Fe/H]-Werte im Bereich zwischen –5,4 und +0,5 für Sterne der Milchstraße und diversen Zwerggalaxien ermittelt.

Während der [Fe/H]-Wert die Metallizität eines Sterns beschreibt, geben andere Verhältnisse wie z.B. [Mg/Fe] an, wie sich die anderen Elemente im Vergleich zu Eisen und zur Sonne verhalten. Ist [Mg/Fe]= 0, ist das Verhältnis von Magnesium zu Eisen genau dasselbe wie in der Sonne. Wäre [Mg/Fe] = +1, würde dies bedeuten, dass der Stern im Vergleich zur Sonne zehnmal mehr Magnesium als Eisen besäße.

Aus der Definition der Klammernotation folgt, dass sich eine Metallizitätsangabe nicht auf die absoluten Verhältnisse der jeweiligen Atome in der Sternatmosphäre bezieht, sondern immer auf den entsprechenden Wert für die Sonne. Astronomen benutzen die Sonne also ständig als Referenzstern. Damit ist auch klar, dass die stellaren Häufigkeiten direkt von den solaren Häufigkeiten abhängen. Ändern sich diese, ändern sich auch die Werte der Sterne. Von Zeit zu Zeit werden die solaren Häufigkeiten in der Tat neu bestimmt. Die sich dabei ergebenden Änderungen spiegeln natürlich keine realen Änderungen in der Sonne wider, sondern zeigen, wie schwierig es auch heute noch ist, die solaren Häufigkeiten, und Sternhäufigkeiten generell, mit sehr hoher Präzision zu messen.

Was passiert nun, nachdem die Elementhäufigkeiten eines Sterns bestimmt wurden? Sie erlauben eine detaillierte Rekonstruktion der Nukleosyntheseprozesse, die in den vorangegangenen Sterngenerationen abgelaufen sind und somit die chemische Entwicklung vorantrieben. Ergebnisse zur Natur der allerersten Sterne im Universum, die mit Hilfe der eisenärmsten Sterne gewonnen werden konnten, werden in Kapitel 9.1 ausgeführt. Kapitel 9.4 beschreibt dann weiter, wie die Häufigkeiten vieler verschiedener metallarmer Sterne mit unterschiedlichen Metallizitäten benutzt werden, um die chemische Entwicklung der leichteren Elemente in der Milchstraße Stück für Stück nachzuvollziehen. Schließlich werden die Entstehung und Entwicklung der Neutroneneinfangelemente, also der schwersten Elemente, in Kapitel 5 im Detail betrachtet.