25 La ecuación de ondas de Schrödinger
Según Einstein y Louis-Victor de Broglie, las partículas y las ondas están íntimamente relacionadas. Las ondas electromagnéticas, incluida la luz, adoptan ambas características e incluso las moléculas y las partículas subatómicas de materia pueden difractar e interferir como ondas.
Pero las ondas son continuas, mientras que las partículas no. Entonces, ¿cómo podemos saber dónde se encuentra una partícula si se propaga en forma de onda? La ecuación de Schrödinger, diseñada por el físico austríaco. Erwin Schrödinger en 1926, describe la probabilidad de que una partícula que se comporta como una onda se encuentre en un punto determinado, utilizando la física de ondas y la probabilidad. Es uno de los fundamentos de la mecánica cuántica, la física del mundo atómico.
La ecuación de Schrödinger se utilizó por primera vez para describir la posición de los electrones en un átomo. Schrödinger trató de describir el comportamiento de los electrones como ondas y también incorporó el concepto de cuantos de energía introducido por Max Planck, la idea de que la energía de ondas se transmite en bloques de construcción básicos cuya energía es proporcional a la frecuencia de las ondas. Los cuantos son los bloques más pequeños, proporcionando una granulación fundamental a cualquier onda.
El átomo de Bohr Fue el físico danés Niels Bohr quien aplicó la idea de la energía cuantizada a los electrones del átomo. Como los electrones son liberados fácilmente del átomo y están cargados negativamente, Bohr pensó que, igual que los planetas giran alrededor del Sol, los electrones orbitan alrededor de núcleos cargados positivamente. Sin embargo, los electrones sólo podían existir con ciertas energías, que correspondían a múltiplos de cuantos básicos de energía. Para los electrones que se encontraban en el interior de un átomo, estos estados de energía deberían restringir a los electrones a distintas capas (u «orbitales») de acuerdo con su energía. Es como si los planetas sólo pudieran encontrarse en ciertos orbitales, definidos por reglas energéticas.
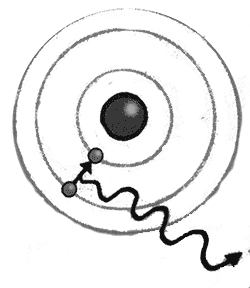
El modelo de Bohr tuvo un gran éxito, especialmente a la hora de explicar el átomo simple de hidrógeno. El hidrógeno contiene un solo electrón que gira alrededor de un único protón, una partícula con carga positiva que actúa como núcleo. La jerarquía de Bohr de energías cuantizadas explicaba conceptualmente las longitudes de onda características de la luz que eran emitidas y absorbidas por el hidrógeno.
Igual que al subir una escalera de mano, si el electrón de un átomo de hidrógeno recibe un impulso energético, puede saltar a un peldaño superior u orbital. Para saltar al peldaño superior el electrón tiene que absorber energía de un fotón que tenga exactamente la energía necesaria para hacerlo. Por lo tanto, hace falta una frecuencia de luz concreta para elevar el nivel energético del electrón. Cualquier otra frecuencia no servirá. Alternativamente, una vez impulsado, el electrón podría volver a saltar al peldaño inferior, emitiendo un fotón de luz de esa frecuencia al hacerlo.
Huellas espectrales Al hacer que los electrones asciendan por la escalera energética, el gas hidrógeno absorbe una serie de fotones de frecuencias características que corresponden a los vacíos energéticos entre los peldaños. Si se proyecta luz blanca a través del gas, estas frecuencias aparecen oscurecidas porque toda la luz se absorbe en cada vacío de frecuencia. En cambio, si el hidrógeno está caliente y sus electrones partieron de los peldaños superiores de la escalera, el resultado son líneas brillantes. Estas energías características del hidrógeno se pueden medir, y están de acuerdo con las predicciones de Bohr. Todos los átomos producen líneas similares, a diferentes energías características. De modo que son huellas diferentes que identifican especies químicas individuales.
Funciones de onda Los niveles energéticos de Bohr funcionaron muy bien para el hidrógeno, pero no así para otros átomos con más de un electrón y con núcleos más pesados. Además, estaba el enigma de De Broglie de que los electrones deberían ser considerados también como ondas. Así que cada orbital electrónico podría considerarse también como un frente de onda. Pero imaginarlo como una onda también implicaba que era imposible determinar dónde se encontraba el electrón en un momento determinado.
En una caja
Una partícula solitaria flotando en el espacio libre tiene una función de onda que recuerda a una onda senoidal. Si está encerrada en una caja, su función de onda debe descender hasta cero en las paredes de la caja y en el exterior porque no puede estar allí. La función de onda en el interior de la caja se puede determinar considerando los niveles permitidos de energía, o cuantos de energía, de la partícula, los cuales tienen que ser siempre mayores que cero. Como la teoría cuántica sólo permite niveles energéticos específicos, es más probable que la partícula se encuentre en unos lugares que en otros, y hay sitios dentro de la caja donde la partícula nunca se encontrará, donde la función de onda es cero. Otros sistemas más complejos tienen funciones de onda que son una combinación de muchas ondas sensoriales y otras funciones matemáticas, como un sonido musical compuesto de numerosos armónicos. En la física convencional, utilizamos las leyes de Newton para describir el movimiento de una partícula en una caja (como un cojinete de bolas en miniatura). En cualquier momento, sabríamos exactamente dónde está y la dirección en que se mueve. Sin embargo, en mecánica cuántica sólo podemos referirnos a la probabilidad de que una partícula se encuentre en un lugar determinado en un momento dado, y como la cuantización de la energía se filtra a escala atómica, hay lugares preferidos en los que se encontrará la partícula. Pero no podemos precisar dónde se encuentra exactamente porque también es una onda.
Schrödinger, inspirado por De Broglie, desarrolló una ecuación que describía la posición de una partícula cuando se comportaba como una onda. Sólo consiguió hacerlo estadísticamente incorporando la probabilidad. La importante ecuación de Schrödinger constituye una parte fundamental de la mecánica cuántica.
«Dios pone a funcionar el electromagnetismo de acuerdo con la teoría de ondas los lunes, miércoles y viernes, y el diablo de acuerdo con la teoría cuántica los martes, jueves y sábados.»
Sir William Bragg, 1862-1942
Schrödinger introdujo la idea de la función de onda para expresar la probabilidad de que la partícula estuviera en un momento determinado y para incluir toda la información posible acerca de esa partícula. Las funciones de onda son notablemente difíciles de comprender, ya que no podemos observarlas a través de nuestra experiencia y nos parecen muy difíciles de visualizar e incluso de interpretar filosóficamente.
El gran avance que auguraba la ecuación de Schrödinger también condujo a modelos de orbitales electrónicos en los átomos. Éstos son perfiles de probabilidad que señalan regiones en las que existe entre un 80 y un 90% de probabilidades de que los electrones se encuentren (planteando la cuestión de que existía una pequeña probabilidad de que se encontraran en otro lugar completamente diferente). Resultó que estos perfiles no eran orbitales esféricos, como Bohr imaginó, sino formas más alargadas, como mancuernas o donuts. Actualmente los químicos utilizan estos conocimientos para diseñar moléculas.
La ecuación de Schrödinger revolucionó la física introduciendo la idea de la dualidad onda-partícula no sólo en los átomos, sino en toda la materia. Junto con Werner Heisenberg y otros, Schrödinger es verdaderamente uno de los padres fundadores de la mecánica cuántica.
Cronología:
1897 d. C.: J. J. Thomson descubre el electrón.
1913 d. C.: Bohr propone los orbitales electrónicos alrededor del núcleo atómico.
1926 d. C.: Schrödinger desarrolla su ecuación de ondas.
La idea en síntesis: aquí, allá, pero no en todas partes