3.6. Implicaciones observacionales.

La cuestión que ahora deseo abordar es si podemos encontrar alguna prueba concreta, ya sea a favor o en contra, de la validez real de la CCC. De entrada, se podría pensar que cualquier prueba respecto a un supuesto «eón» existente antes de nuestro Big Bang debe estar fuera del acceso observacional, debido a las temperaturas absolutamente enormes que aparecen en el Big Bang y que parecerían borrar cualquier información, lo que nos separaría de toda esa supuesta actividad previa. No obstante, deberíamos tener en cuenta que tiene que haber una extrema organización presente en el Big Bang, como consecuencia directa de la Segunda Ley, y los argumentos de este libro apuntan a que esta organización tenga un carácter que permite que nuestro Big Bang se extienda de manera conforme a un eón previo al nuestro, y que esta extensión esté gobernada por una evolución determinista muy específica. Por consiguiente, podemos confiar en que haya alguna manera de que ¡realmente fuéramos capaces de «ver» ese eón anterior!

Debemos preguntar qué propiedades concretas del futuro remoto de un eón anterior al nuestro podrían ser observables para nosotros. Una cosa de la que podemos estar seguros, si la CCC es correcta, es que la geometría espacial general de nuestro propio eón debe empalmar con la del eón previo. Si el eón previo fuera espacialmente finito, por ejemplo, así debería serlo el nuestro. Si ese eón anterior coincidiera, en una gran escala, con una 3-geometría espacial euclidiana (K = 0), entonces eso también sería válido para el nuestro, y si tuviera una geometría espacial hiperbólica (K < 0), entonces el nuestro también sería hiperbólico. Todo esto se sigue porque la geometría espacial, en general, está determinada por la de la 3-superficie de tránsito, siendo la geometría de esta 3-superficie común a los dos eones que limita. Por supuesto, esto no nos ofrece nada nuevo de valor observacional, porque no tenemos información independiente sobre la geometría espacial general del eón previo.

En una escala algo menor, sin embargo, las distribuciones de materia podrían reordenarse a lo largo del progreso de cada eón, de acuerdo con algunos quizá complicados, pero en principio comprensibles, procesos dinámicos. El comportamiento final de estas distribuciones de materia, que toman la forma de radiación sin masa (de acuerdo con los requisitos de la CCC en §3.2), puede dejar su firma en la 3-superficie de tránsito, y entonces quizá pueda leerse en las sutiles irregularidades en el CMB. Nuestra tarea consistiría en tratar de adivinar cuáles serían, a este respecto, los procesos más importantes que tienen lugar en el curso del eón previo, y tratar de descifrar las señales ocultas en esas minúsculas irregularidades en el CMB.

Para ser capaces de interpretar señales de este tipo necesitaríamos tener una buena comprensión de los fenómenos que serían su causa probable. Para ello, necesitaríamos examinar cuidadosamente los procesos dinámicos que podrían estar implicados en el eón previo, y también cómo podrían propagarse las cosas de un eón al siguiente. Sin embargo, para llegar a conclusiones razonablemente claras acerca de la naturaleza detallada del eón previo nos sería de ayuda el que podamos suponer que, en general, era esencialmente similar al nuestro. Entonces podemos considerar que el eón previo al nuestro se habría comportado en estrecho acuerdo con el tipo de comportamiento que vemos en el universo que nos rodea, y con la forma general con la que esperamos que evolucione en el futuro.

Y lo que es más evidente, esperaríamos que hubiera habido una expansión exponencial en el futuro remoto del eón previo, donde estamos suponiendo que una constante cosmológica positiva dominaba el comportamiento de dicho eón en su muy remoto futuro, como parece ser el caso de nuestro propio eón (si consideramos que Λ es constante). La resultante expansión exponencial de dicho eón anterior guardaría una tentadora similitud con la supuesta fase inflacionaria de la imagen actualmente preferida de la historia muy temprana del universo, aunque esta imagen actualmente convencional afirma que la expansión exponencial tiene lugar entre unos 10⁻³² s y 10⁻³⁶ s en nuestro propio eón (véanse §2.1 y §2.6), muy poco después del propio Big Bang. Por el contrario, la CCC situaría esta «fase inflacionaria» antes del Big Bang, identificándola con la expansión exponencial del futuro remoto del eón previo. De hecho, como se ha mencionado en §3.3, una idea de esta naturaleza fue propuesta por Gabriele Veneziano en 1998,^[3.81] aunque su esquema dependía fuertemente de ideas de la teoría de cuerdas.

Fig. 3.23. Las cosmologías (preinflacionarias) estándar podrían implicar que puntos en el CMB celestes, más alejados que los dados por ω = 2° en la figura, no deberían estar correlacionados (puesto que los conos de luz pasados de q y r no se cortan), mientras que tales correlaciones se observan hasta ~60°, como sucede con puntos como p y r.

Un aspecto importante de esta idea general es que dos pruebas observacionales clave que parecían proporcionar un apoyo crucial para la imagen ahora estándar de la cosmología inflacionaria, como se deducen de las ligeras variaciones de temperatura vistas en el CMB, parecen ser también abordadas por teorías pre-Big-Bang de esta naturaleza. Una de éstas es que existen correlaciones observadas en las variaciones de temperatura en el CMB sobre ángulos en el cielo (hasta unos 60°, de hecho) que serían incompatibles con las cosmologías estándar de tipo Friedmann o Tolman (§2.1 y §3.3), si se considera que el propio Big Bang está intrínsecamente libre de correlaciones. Esta incompatibilidad se muestra en los diagramas conformes esquemáticos de la Fig. 3.23, donde vemos que la superficie de última dispersión (desacoplamiento; véase §2.2) ocurre demasiado próxima a la 3-superficie Big Bang ⁻ para que efectos que vistos desde nuestra posición parecen estar separados más de unos 2° en el cielo hayan estado nunca en contacto causal. Esto supone que todas esas correlaciones surgen de procesos que ocurren después del Big Bang, y los diferentes puntos de ⁻ están de hecho completamente descorrelacionados. La inflación puede conseguir tales correlaciones porque la «fase inflacionaria» aumenta la separación entre ⁻ y ⁻ en un diagrama conforme,^[3.82] de modo que ángulos mucho mayores vistos desde nuestra posición se ponen en contacto causal; véase la Fig. 3.24.

Fig. 3.24. Un efecto de la inflación es aumentar la separación entre y , de modo que pueden darse las correlaciones de la Fig. 3.23.

El otro elemento de prueba clave, que parece dar un fuerte apoyo a la inflación, es que las fluctuaciones de densidad iniciales —que dan lugar a fluctuaciones de temperatura en el CMB— parecen ser invariantes frente a escala, en un rango muy amplio. La explicación que da la cosmología inflacionaria es que muy poco después del Big Bang había irregularidades iniciales completamente aleatorias —de naturaleza de fluctuaciones cuánticas inicialmente minúsculas en el «campo inflatón» (§2.6)— y que luego dominó la expansión exponencial inflacionaria, que expandió enormemente dichas irregularidades de modo que se transformaron finalmente^[3.83] en las irregularidades de densidad actuales en la distribución de materia (principalmente oscura). Ahora bien, una expansión exponencial es un proceso autosimilar, de modo que uno puede imaginar que si hay aleatoriedad en la forma en la que las fluctuaciones iniciales están distribuidas en el espacio-tiempo, entonces el resultado de la actuación exponencial sobre dichas fluctuaciones será una distribución con cierta invariancia de escala. De hecho, mucho antes de que se hubiera propuesto el esquema inflacionario, E. R. Harrison y Y. B. Zel’dovich habían propuesto, en 1970, que las desviaciones de la uniformidad observadas en la primitiva distribución de materia en el universo podían explicarse si se supusiera que las fluctuaciones iniciales son invariantes frente a escala. No solo la inflación había dado un argumento lógico para esta suposición, sino que análisis de observaciones posteriores del CMB confirmaron una práctica invariancia de escala sobre un rango aún mucho más amplio que antes, lo que daba apoyo considerable a la idea inflacionaria, especialmente dado que había sido difícil ver qué otro tipo de explicación podía dar una base teórica a esta invariancia de escala observada.

De hecho, si se va a rechazar la imagen inflacionaria hay que encontrar alguna explicación alternativa tanto para la invariancia de escala como para las correlaciones más allá del tamaño del horizonte en las irregularidades de densidad iniciales. En la CCC (como en el esquema anterior de Veneziano) estos dos puntos se tratan desplazando la fase inflacionaria del universo de manera que de ocurrir en un momento que sigue inmediatamente al Big Bang pasa a ocurrir en una fase de expansión que precede al Big Bang, tal como se ha descrito antes. Puesto que seguimos teniendo una fase de universo en expansión efectivamente autosimilar, igual que lo que sucede con inflación, cabe esperar que esto podría llevar a fluctuaciones de densidad con una naturaleza invariante frente a escala. Además, de nuevo cabe esperar correlaciones fuera de la escala del horizonte de los modelos de Friedmann o Tolman, pero ahora estas correlaciones se establecen a través de sucesos que tuvieron lugar en el eón previo al nuestro. Véase la Fig. 3.25.

Para ser más explícito acerca de cuáles serían probablemente estos sucesos, según la CCC, debemos tratar de entender cuáles van a ser probablemente los procesos más relevantes que tienen lugar en el eón previo al nuestro. Antes de que podamos entrar en gran detalle, debemos abordar una pregunta especialmente importante. Pues existe la posibilidad, señalada en §3.3, de que tengamos que tomar en serio la sugerencia de John A. Wheeler de que las constantes fundamentales de la naturaleza pudieran no haber tenido exactamente los mismos valores en el eón previo que los que tienen en el nuestro. La más obvia (y más simple) de tales posibilidades sería que el gran número N, mencionado al final de §3.2, que en nuestro eón toma el valor N ~ 10²⁰, podría tomar otro valor en el eón previo. Hay, por supuesto, dos caras en esta cuestión. Ciertamente haría la vida más fácil si solo podemos suponer que constantes numéricas fundamentales tales como N tenían el mismo valor en el eón previo que en el nuestro, o que las observaciones serían insensibles a alteraciones (razonables) en los valores de tales números. Pero, por otra parte, si cambiar un número tal como N pudiera tener efectos claramente distinguibles, entonces existe la posibilidad potencialmente excitante de determinar realmente si un número semejante podría ser o no una constante fundamental (quizá calculable matemáticamente en principio) o si realmente cambia de un eón a otro, posiblemente de una manera matemática específica que podría estar ella misma sujeta a un test observacional.

Fig. 3.25. En la CCC, las correlaciones requeridas de la Fig. 3.23 pueden ser resultado de actividades en el eón previo.

Un conjunto complementario de preguntas están relacionadas con nuestras expectativas sobre la evolución de nuestro propio eón en el futuro muy remoto. Aquí, los requisitos y expectativas de la CCC son algo más claros. En concreto, Λ debe ser realmente una constante cosmológica, y nuestro eón continúa su expansión exponencial por toda la eternidad. La evaporación de Hawking de los agujeros negros debe ser una realidad y debe continuar hasta que todos los agujeros hayan desaparecido, depositando virtualmente toda su energía en reposo en fotones de baja energía y radiación gravitatoria; y esto ocurrirá incluso para los agujeros más grandes que cabe esperar que aparezcan, hasta que finalmente desaparecen. ¿Podría esta radiación de Hawking ser realmente detectable si ocurre en el eón previo al nuestro? Debemos tener en cuenta que toda la masa-energía de un agujero negro, por muy grande que pudiera ser inicialmente, tendría que depositarse en última instancia en esta radiación electromagnética de baja frecuencia. Esta energía encontraría finalmente su camino a la superficie de tránsito y dejaría su huella sutil en el CMB de nuestro propio eón. No es en absoluto descartable, si la CCC es correcta, que esta información pudiera finalmente reconstruirse a partir de las minúsculas irregularidades en el CMB. Esto sería muy notable, si sucede, puesto que normalmente se consideraría que la radiación de Hawking en nuestro propio eón ¡tiene un efecto tan absurdamente minúsculo que sería por completo inobservable!

Una consecuencia menos convencional de la CCC es que las masas en reposo de todas las partículas deberían desaparecer finalmente en los vastos abismos de eternidad (§3.2), de modo que en el límite asintótico todas las partículas supervivientes, incluidas las cargadas, serían partículas sin masa. Según este esquema, la desintegración de la masa en reposo sería una característica universal de las partículas masivas, de modo que cabría imaginar que fuera un efecto observable. Sin embargo, en nuestro estado de conocimiento presente, el esquema no ha proporcionado ninguna receta del ritmo al que debería desintegrase la masa. El ritmo de desintegración podría muy bien ser extraordinariamente lento, y entonces sería difícil defender que el hecho de que todavía no se haya observado tal desintegración es una prueba en contra de este aspecto de la CCC. Un punto digno de mención aquí es que si todos los diferentes tipos de partículas tienen ritmos de desintegración de masa aproximadamente proporcionales a las masas respectivas, entonces el efecto se parecería a un debilitamiento muy lento de la constante gravitatoria. Hasta 1998,^[3.84] la mejor cota experimental para un ritmo de decaimiento de la constante gravitatoria fija un valor menor que aproximadamente 1,6 × 10⁻¹² por año. Sin embargo, debemos tener presente que una escala de tiempo de 10¹² años es una minucia comparada con los períodos de tiempo de al menos 10¹⁰⁰ años que es necesario considerar para permitir que desaparezcan todos los agujeros negros. Cuando escribo esto no conozco ninguna propuesta observacional precisa que pusiera a prueba seriamente el aspecto de la CCC que demanda la desintegración final de la masa en reposo.

Hay, sin embargo, una clara consecuencia de la CCC que debería poder dirimirse mediante un análisis apropiado del CMB. El efecto en cuestión es la radiación gravitatoria producida por encuentros de agujeros negros extremadamente masivos (principalmente los que se localizan en los centros galácticos). ¿Cuál sería el resultado de tales encuentros? Si los agujeros pasaran muy cerca uno del otro, cabría esperar que cada uno de ellos desviaría el movimiento del otro de forma suficientemente violenta para que hubiera una ráfaga de radiación gravitatoria que podría llevarse una cantidad importante de energía del par, y sus movimientos relativos quedarían reducidos de forma apreciable. Si se acercaran todavía más, entonces podrían quedar mutuamente atrapados en órbitas uno alrededor del otro, que se harían cada vez más cerradas por pérdida de energía en ondas gravitatorias, de lo que resultaría una enorme pérdida de energía total hasta que se engulleran mutuamente para formar un único agujero negro. En casos extremos, este único agujero podría ser el resultado de un impacto directo, y el agujero resultante estaría inicialmente fuertemente distorsionado antes de que el agujero se asentara mediante la radiación gravitatoria. En cualquier caso, habría una enorme emisión de ondas gravitatorias que probablemente se llevaría una nada despreciable proporción de la enorme masa combinada de los dos agujeros.

Fig. 3.26. Encuentros entre enormes agujeros negros en el eón previo darían como resultado ráfagas notables de radiación gravitatoria. Esto se manifestaría como un círculo de temperatura aumentada o disminuida (dependiendo de la geometría general) en el CMB del cielo.

En una escala de tiempo como la que aquí nos interesa, toda esta ráfaga de ondas gravitatorias sería prácticamente instantánea. En ausencia de otros grandes efectos distorsionadores a lo largo del universo, esta radiación estaría esencialmente contenida dentro de una fina capa casi esférica que se dispersa para siempre, desde el punto de encuentro e, a la velocidad de la luz. En términos de una imagen conforme (esquemática) esta ráfaga de energía estaría representada como un cono de luz hacia fuera ⁺(e) que se extiende desde e a ^{^} (donde ^{^} es el «⁺» del eón previo al nuestro). Aunque podría pensarse que esta radiación se atenuaría indefinidamente con el paso del tiempo, hasta ser por completo insignificante cuando finalmente se alcanza ^{^}, si examinamos la situación de la forma correcta encontramos que en realidad no es así. Recordemos de §3.2 que el campo gravitatorio puede describirse por un -tensor K, que satisface una ecuación de ondas conformemente invariante ∇K = 0. Puesto que esta ecuación de ondas es conformemente invariante, podemos considerar que K se propaga en el espacio-tiempo mostrado en la Fig. 3.26, donde podemos tomar la frontera futura ^{^} como una 3-esfera de tipo espacio ordinaria. La onda llega a ^{^} en un período finito, y K tiene allí un valor finito que puede estimarse a partir de la geometría de la Fig. 3.26.

Ahora bien, debido a la relación entre K y el tensor conforme C en el escalado de la métrica conforme que utilizaríamos para la Fig. 3.26 (el «Ĉ = Ω» de §3.2), encontramos que el tensor conforme C alcanza el valor cero en ^{^}, pero tiene una derivada normal distinta de cero a través de ^{^} (véase la Fig. 3.27; compárese con la Fig. 3.6).A partir de los argumentos del apéndice B12 encontramos que la presencia de esta derivada normal tiene dos efectos directos. Uno de éstos es influir en la geometría conforme de la superficie de tránsito (^{^}/⁻), mediante una magnitud de curvatura conforme conocida como el tensor de «Cotton-York», de modo que no podemos esperar que la geometría espacial del eón sucesivo (el nuestro) sea exactamente del tipo FLRW en el momento del Big Bang, sino que debe haber ligeras irregularidades. El segundo efecto, y más inmediatamente observable, sería dar al material del ϖ-campo —que, en §3.2, se ha argumentado que es la fase inicial de nueva materia oscura— un importante «empujón» en la dirección de la radiación; véase la Fig. 3.27.

Fig. 3.27. Cuando la ráfaga de ondas gravitatorias encuentra a la 3-superficie de tránsito, da al material inicial del eón sucesivo un «empujón» en la dirección de la onda.

Si el punto u representa nuestra localización actual en el espaciotiempo, entonces el cono de luz pasado ⁻(u) de u representa esa parte del universo que podemos «ver» directamente. La intersección de ⁻(u) con la superficie de desacoplamiento representa así lo que se puede observar directamente en el CMB, pero puesto que en una representación conforme estricta está muy próxima (a aproximadamente un 1 por ciento de la altura total del eón entero, en la figura) a la superficie de cruce ⁻; no nos equivocaremos demasiado^[3.85] si consideramos esto como la intersección de ⁻(u) con ⁻. Ignorando posibles efectos de no uniformidad de la densidad de materia dentro de nuestro propio eón, esto será una esfera geométrica. El cono de luz futuro ⁺(e) de e también cortará a ^{^} (= ⁻) en una esfera geométrica, suponiendo que podamos ignorar la no uniformidad de densidad en este eón previo. Así pues, la parte de la radiación procedente del encuentro del agujero negro en e que es directamente visible para nosotros a través de su efecto en el CMB será la intersección de estas dos esferas en ⁻, siendo esta intersección un círculo geométrico preciso C, donde estoy ignorando la pequeña diferencia entre las 3-superficies ⁻ y ⁻

El «empujón» que la ráfaga de ondas gravitatorias impartirá a la (presunta) materia oscura primordial tendrá una componente en nuestra dirección que podría ser hacia nosotros o podría alejarse de nosotros, dependiendo de la relación geométrica entre u, e y la superficie de tránsito. Este efecto de ser hacia nosotros o alejarse de nosotros sería el mismo a lo largo de todo el círculo C. Así pues, esperamos que para cada uno de estos encuentros de agujeros negros en el eón previo, para el que se cortan estas dos esferas, habría un círculo en el CMB del cielo que contribuye o positiva o negativamente a la temperatura del CMB promediada sobre el cielo

Como analogía útil, imaginemos un estanque sobre el que cae una lluvia ligera, en un día tranquilo y sin viento. Cada gota de lluvia provocará una onda circular que se mueve hacia fuera desde el punto de impacto; pero si hay muchos de estos impactos pronto será difícil distinguir las ondas individuales que continuamente se mueven hacia fuera y se solapan de formas complicadas. Cada impacto debe considerarse análogo a uno de los encuentros de agujeros negros antes imaginados. Al cabo de un tiempo, la lluvia cesa (el equivalente a la desaparición final de los agujeros negros mediante evaporación de Hawking) y nos quedamos con una pauta de ondas de aspecto aleatorio, de modo que a partir de una fotografía de dicha pauta sería difícil averiguar que había sido producida de esa manera. No obstante, si se realiza un análisis estadístico adecuado de esa pauta, debería ser posible (si la lluvia no se ha prolongado durante mucho tiempo) reconstruir la configuración espaciotemporal de los impactos de las gotas de lluvia originales y confiar en que la pauta ha aparecido realmente a partir de impactos discretos de este tipo.

A mí me parecía que un análisis estadístico del CMB debería proporcionar un buen test de la propuesta CCC. Por ello, al tener la ocasión de visitar la Universidad de Princeton a principios de mayo de 2008, aproveché la oportunidad para consultar a David Spergel, que es un experto mundial en el análisis de datos del CMB. Le pregunté si alguien había visto un efecto semejante en los datos del CMB, a lo que él respondió «No»; después de lo cual añadió, «pero nadie ha mirado hasta ahora». Más tarde, él planteó el problema a uno de sus ayudantes posdoctorales, Amir Hajian, quien posteriormente llevó a cabo un análisis preliminar de los datos observacionales proporcionados por el satélite WMAP para tratar de ver si hay alguna evidencia de un efecto de este tipo.

Lo que hizo Hajian fue escoger una serie de radios alternativos, empezando en un radio angular de aproximadamente 1° y luego aumentando este radio en pasos de aproximadamente 0,4° hasta llegar a un radio angular de aproximadamente 60° (para 171 radios diferentes en total). Para cada radio dado, se calculaba la temperatura CMB promedio a lo largo de círculos de este radio centrados en 196.608 puntos diferentes uniformemente dispersos sobre el cielo. Luego se construía un histograma para ver si había alguna desviación significativa respecto de lo que cabía esperar del «comportamiento gaussiano» de datos completamente aleatorios. Al principio se veían ciertos «picos» que parecían presentar una clara evidencia de varios círculos individuales de la naturaleza predicha por la CCC. Sin embargo, pronto quedó claro que eran completamente espurios, pues los círculos en cuestión cruzaban ciertas regiones del cielo, algunas de ellas relacionadas con el posicionamiento de nuestra Vía Láctea, que se sabía que eran más calientes o más frías que el cielo CMB normal. Para eliminar tales efectos había que suprimir la información de regiones próximas al plano galáctico, y así se eliminaron efectivamente los «picos» espurios.

Un punto digno de mención en esa etapa es que, en cualquier caso, muchos de los círculos que daban las picos tenían radios de más de 30° en el cielo, y no deberían haber aparecido en ningún caso, según la CCC, si realmente el eón previo al nuestro tuvo una historia general más o menos similar a la que se prevé para nuestro propio eón. La razón para ello es que los encuentros de agujeros negros galácticos que se consideran aquí no deberían haber aparecido antes de lo que hubiera sido «el tiempo presente» en el eón previo, que en nuestro eón ocurre a aproximadamente 2/3 del camino en el diagrama conforme (Fig. 3.28). simple geometría (véase la Fig. 3.29) muestra que los encuentros de agujeros negros, con e ocurriendo más tarde que 2/3 del camino en el diagrama conforme del eón previo, darían lugar necesariamente a círculos de radios menores que 30° desde nuestra posición en u (en desacuerdo con muchos de los picos). Por consiguiente, las correlaciones de temperaturas que podrían producir estos efectos no se extenderían en la esfera celeste tanto como 60°. Es un hecho curioso que correlaciones en la temperatura del CMB observada sí parecen decaer a unos 60°, lo que no se explica en la imagen inflacionaria estándar, hasta donde yo sé, y quizá puede considerarse que esto representa un apoyo para la propuesta CCC.

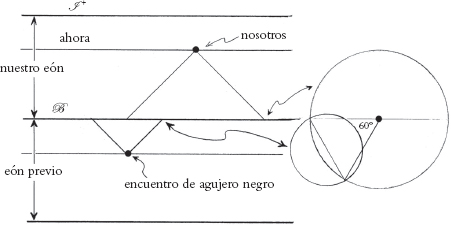
Fig. 3.28. Parece que estamos a aproximadamente 2/3 del camino en nuestro eón, en un diagrama conforme. Si esto es válido también para los primeros encuentros de agujeros negros en el eón previo, entonces cabe esperar un corte en las correlaciones angulares a 60°.

Con la eliminación de estos picos, parece que siguen quedando varias desviaciones sistemáticas aparentemente significativas respecto a la aleatoriedad gaussiana en el análisis de Hajian. Tales desviaciones, que implican un aparente exceso de círculos fríos en un rango de radios angulares entre aproximadamente 7° y 15°, parecían en particular notables y, en mi opinión, requerían explicación. Pudiera ser que estos efectos fueran el resultado de algunos ingredientes espurios que no tienen nada que ver con la CCC, pero me parecía que una cuestión crucial era si las desviaciones de la aleatoriedad tenían que ver específicamente con el hecho de que las regiones del cielo sobre las que se estaba promediando eran realmente círculos y no alguna otra forma, pues la naturaleza circular real de las presuntas perturbaciones en el CMB parecerían ser una característica de esta predicción de la CCC. Por consiguiente, sugerí que se repitiera al análisis, pero con un «giro» que conserva el área aplicado a la esfera celeste (véase la Fig. 3.29), de modo que círculos reales en la esfera celeste parecerían tener una forma más elíptica según el análisis. Yo había propuesto que se hicieran tres versiones diferentes del análisis, una sin giro celeste, otra con un pequeño giro, y otra con un giro mayor. Había previsto que la CCC debería predecir que el efecto no gaussiano debería ser máximo cuando no hay giro, algo reducido cuando hay un giro pequeño, y quizá totalmente ausente con el giro grande.

Fig. 3.29. Girando el CMB en coordenadas polares esféricas (utilizando la fórmula Θ′ = Θ, φ′ = φ + 3aπΘ² – 2aΘ³). Esto convierte los círculos en formas más elípticas.

Sin embargo, el resultado de este análisis (realizado por Hajian en el otoño de 2008) me sorprendió. De forma sistemática sobre el rango de radios de 8,4° a 12,4° (que englobaban 12 histogramas distintos sucesivos), la pequeña cantidad de giro celeste aumentaba en realidad este efecto particular de forma muy clara, mientras que el giro celeste más grande hacía que desapareciera. En otras partes de los histogramas había indicios similares de una sensibilidad a la circularidad de la forma que se estaba examinando. Al principio quedé algo perplejo por este hallazgo, al ser incapaz de imaginar cómo podía explicarse la ampliación debida a la pequeña cantidad de giro, pero luego se me ocurrió la posibilidad de que hubiera grandes inhomogeneidades en la distribución de masa (preferiblemente) en nuestro propio eón que sirven para distorsionar ligeramente imágenes circulares y transformarlas en elípticas.^[3.86] Recordemos de §2.6 las importantes distorsiones de imágenes que puede producir la presencia de curvatura de Weyl (véase la Fig. 2.49). La ampliación del efecto que había producido el pequeño giro podía aparecer (según la imagen que yo sugería) de un fortuito acuerdo, en algunas regiones del cielo, entre la cantidad de giro celeste artificial que se había introducido y la distorsión real debida a curvatura de Weyl. En otras regiones el giro llevaría a mayor desacuerdo, pero el efecto bien podría ser una ampliación general, en circunstancias apropiadas, pues los debidos al desacuerdo podrían perderse fácilmente en el «ruido».

Por desgracia, la probable presencia de distorsiones significativas, debidas a la curvatura de Weyl interpuesta, complica considerablemente el análisis. Podría ser útil descomponer el cielo en regiones más pequeñas para tratar de identificar dónde podría haber curvatura de Weyl importante a lo largo de la visual entre u y la 3-superficie de desacoplamiento . Quizá esto podría relacionarse con inhomogeneidades conocidas en la distribución de masa en el universo (por ejemplo, los grandes «vacíos»^[3.87]). En cualquier caso, hay algo tentador en la situación en la que parecen habernos dejado las observaciones por el momento. Ciertamente hay que esperar que estas cuestiones se aclaren en un futuro no demasiado lejano, y que no pase mucho tiempo antes de que se pueda establecer claramente el estatus físico de la cosmología cíclica conforme.