1.3. El espacio de fases y la definición de Boltzmann para la entropía

No obstante, todavía no hemos acabado con la definición de entropía; lo que se ha dicho hasta ahora sólo aborda a medias la cuestión. Podemos ver que la descripción que he dado no es del todo adecuada si consideramos un ejemplo ligeramente diferente. En lugar de tener una lata de pintura roja y azul, podríamos considerar una botella llena con una mitad de agua y otra mitad de aceite de oliva. Podemos removerla tanto como queramos y también agitarla violentamente, pero cuando dejamos de hacerlo el agua y el aceite vuelven a separarse, y pronto tenemos sólo aceite de oliva en la mitad superior y agua en la mitad inferior. Sin embargo, la entropía ha estado aumentando continuamente durante el proceso de separación. El nuevo ingrediente que interviene aquí es una fuerte atracción mutua entre las moléculas de aceite que hace que se agreguen y expulsen el agua al hacerlo. La mera noción de espacio de configuración no es adecuada para dar cuenta del aumento de entropía en una situación de este tipo, pues necesitamos tener en cuenta los movimientos de las partículas/moléculas individuales, y no sólo sus localizaciones. En cualquier caso, sus movimientos serán necesarios para nosotros, de modo que la evolución futura del estado está determinada de acuerdo con las leyes newtonianas que suponemos son las que actúan aquí. En el caso de las moléculas del aceite de oliva, su fuerte atracción mutua hace que sus velocidades aumenten (en vigorosos movimientos orbitales una alrededor de otra) a medida que se aproximan, y es la parte de «movimiento» del espacio relevante la que proporciona el necesario volumen extra (y por consiguiente entropía extra) para las situaciones en que el aceite de oliva está completamente agregado.

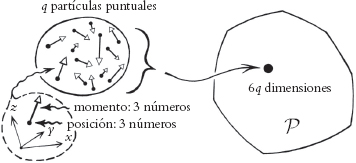
Fig. 1.6. El espacio de fases tiene el doble de dimensiones que .

El espacio que necesitamos, en lugar del espacio de configuración antes descrito, es lo que se denomina espacio de fases. El espacio de fases tiene el doble de dimensiones (!) que , y por cada coordenada de posición para cada partícula (o molécula) constituyente debe haber una correspondiente coordenada de «movimiento» además de dicha coordenada de posición (véase la Fig. 1.6). Cabría imaginar que una coordenada apropiada sería una medida de la velocidad (o de la velocidad angular, en el caso de coordenadas angulares que describen la orientación en el espacio). Sin embargo, resulta que debido a profundas conexiones con el formalismo de la teoría hamiltoniana,^[1.1] es el momento (o el momento angular en caso de coordenadas angulares) lo que necesitaremos para describir el movimiento. En la mayoría de las situaciones familiares, todo lo que necesitamos saber sobre esta noción de «momento» es que es el producto de la masa por la velocidad (como ya se ha mencionado en §1.1). Ahora los movimientos (instantáneos), así como las posiciones, de todas las partículas que componen nuestro sistema están codificados en la localización de un único punto p en . Decimos que el estado de nuestro sistema está descrito por la localización de p dentro de .

Podemos considerar que las leyes dinámicas que gobiernan el comportamiento de nuestro sistema son las leyes newtonianas del movimiento, pero también podemos tratar situaciones más generales tales como los campos continuos de la electrodinámica de Maxwell (véanse §2.6, §3.1, §3.2 y el apéndice A1), que también entran bajo el amplio marco hamiltoniano que se ha mencionado antes. Estas leyes son deterministas en el sentido de que el estado de nuestro sistema en cualquier instante determina por completo el estado en cualquier otro instante, ya sea anterior o posterior. Para decirlo de otra manera, podemos describir la evolución dinámica de nuestro sistema, de acuerdo con estas leyes, como un punto p que se mueve a lo largo de una curva —llamada curva de evolución— en el espacio de fases . Esta curva de evolución representa la única evolución del sistema entero, de acuerdo con las leyes dinámicas, que parte de un estado inicial dado, que podemos representar por un punto concreto p₀ en el espacio de fases . (Véase la Fig. 1.7.) De hecho, todo el espacio de fases estará lleno (técnicamente, foliado) de tales curvas de evolución (parecido a una bala de paja) y cada punto de estará en alguna curva de evolución particular. Debemos considerar que esta curva está orientada, lo que significa que debemos asignar una dirección a la curva, y podemos hacerlo poniéndole una flecha. La evolución de nuestro sistema, de acuerdo con las leyes dinámicas, se describe por un punto p en movimiento, que viaja a lo largo de la curva de evolución —en este caso partiendo del punto particular p₀— y se mueve en la dirección en que apunta la flecha. Esto nos proporciona la evolución futura del estado particular del sistema representado por p. Seguir la curva de evolución en la dirección que se aleja de p₀ en sentido contrario a la flecha nos da la inversa temporal de la evolución, que nos dice cómo se habría llegado al estado representado por p₀ a partir de estados en el pasado. De nuevo, esta evolución sería única, según las leyes dinámicas.

Fig. 1.7. El punto p se mueve a lo largo de una curva de evolución en el espacio de fases .

Una propiedad importante del espacio de fases, que conocemos desde la llegada de la mecánica cuántica, es que tiene una medida natural, de modo que podemos tomar volúmenes en el espacio de fases como si fueran, esencialmente, simples números adimensionales. Esto es importante, porque la definición de Boltzmann para la entropía, a la que pronto llegaremos, viene dada en términos de volúmenes del espacio de fases, de modo que tenemos que ser capaces de comparar medidas de volúmenes de altas dimensiones, y las dimensiones pueden diferir mucho de un volumen a otro. Esto puede parecer extraño desde el punto de vista de la física clásica ordinaria (es decir, no cuántica), puesto que en términos ordinarios consideraríamos que la longitud de una curva (un «volumen» 1-dimensional) tiene siempre una medida menor que el área de una superficie (un «volumen» 2-dimensional), y que el área de una superficie tiene una medida menor que un 3-volumen, etc. Pero las medidas de volúmenes del espacio de fases que la mecánica cuántica nos dice que utilicemos son simplemente números, medidos en unidades de masa y distancia que nos dan ℏ = 1, siendo

la versión de Dirac de la constante de Planck (a veces llamada constante de Planck «reducida»), donde h es la constante de Planck original. En unidades estándar h tiene el valor extraordinariamente minúsculo

ℏ = 1,05457… × 10⁻³⁴ julios · segundo,

de modo que las medidas del espacio de fases que encontramos en circunstancias ordinarias suelen tener valores numéricos extraordinariamente altos.

Pensar que estos números son simplemente enteros da cierta «granularidad» al espacio de fases, y esto proporciona el carácter discreto de los «quanta» de la mecánica cuántica. Pero en la mayoría de las circunstancias ordinarias estos números serían enormes, de modo que la granularidad y la discretización pasan inadvertidas. Una excepción surge con el espectro de cuerpo negro de Planck al que llegaremos en §2.2 (véanse la Fig. 2.6 y la nota ^[1.2]); éste es el fenómeno observado cuya explicación por Max Planck, en 1900, puso en marcha la revolución cuántica. Aquí hay que considerar una situación de equilibrio que implica simultáneamente diferentes números de fotones, y por consiguiente espacios de fases de diferentes dimensiones. La discusión adecuada de tales materias está fuera del alcance de este libro, pero volveré a las ideas básicas de la teoría cuántica en §3.4.^[1.3]

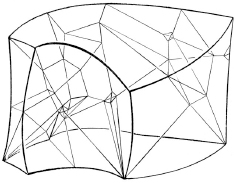
Fig. 1.8. Una impresión de granulado grueso en dimensiones más altas.

Ahora que tenemos la noción de espacio de fases de un sistema, tendremos que entender cómo opera la Segunda Ley en relación con él. Como sucedía con mi argumentación anterior del espacio de configuración, esto requerirá que dispongamos de un granulado grueso de , en donde dos puntos que pertenezcan a la misma región de grano grueso se considerarán «indistinguibles» con respecto a parámetros macroscópicos (tales como temperatura, presión, densidad, dirección y magnitud del flujo de un fluido, color, composición química, etc.). La definición de la entropía S de un estado representado por un punto p en la proporciona ahora la notable fórmula de Boltzmann

S = k' log₁₀ V,

donde V es el volumen de la región de grano grueso que contiene a p. La cantidad k′ es una constante pequeña dada por k′ = klog10 (log10 = 2,302 585…), donde k es realmente la constante de Boltzmann, que tiene el valor minúsculo

k = 1,3805… × 10⁻²³ julios/grado Kelvin,

y así k′ = 3,179… × 10⁻²³ JK⁻¹ (véase la Fig. 1.8). De hecho, para ser consistentes con las definiciones utilizadas normalmente por los físicos, en lo sucesivo escribiré las fórmulas en términos de logaritmos naturales, de modo que la fórmula de la entropía de Boltzmann queda

S = k log V,

donde logV = 2,302 585… × log₁₀V.

Antes de que pasemos a examinar, en §1.4, las razones y las implicaciones de esta elegante definición, y qué relación tiene con la Segunda Ley, debería mencionar una cuestión concreta que la definición aborda de forma muy adecuada. A veces se señala (muy correctamente) que el bajo valor de la entropía de un estado no es realmente una buena medida de la «especialidad» del estado. Si consideramos de nuevo la situación del huevo que cae que se ha introducido en §1.1, advertimos que el estado de entropía relativamente alta al que se llega cuando el huevo se ha convertido en un amasijo en el suelo sigue siendo un estado extraordinariamente especial. Es especial porque hay unas correlaciones muy particulares entre los movimientos de las partículas que constituyen ese aparente «amasijo», de una naturaleza tal que si las invertimos a todas, entonces ese amasijo tendrá la notable propiedad de que rápidamente se resolverá en un huevo perfectamente completo que se proyecta hacia arriba para posarse con delicadeza en la mesa. Éste es en verdad un estado muy especial, no menos especial que lo era la configuración de entropía relativamente baja del huevo sobre la mesa con que empezamos. Pero por «especial» que fuera sin duda ese estado que consiste en un amasijo en el suelo, no era especial en el sentido particular al que nos referimos al decir que tiene «baja entropía». El bajo valor de la entropía se refiere a una especialidad manifiesta, que se muestra en valores especiales de los parámetros macroscópicos. Las sutiles correlaciones entre los movimientos de las partículas no tienen importancia cuando se trata de la entropía que hay que asignar al estado de un sistema.

Vemos que aunque algunos estados de entropía relativamente alta (tales como el huevo aplastado invertido en el tiempo que acabamos de considerar) pueden evolucionar hacia estados de entropía más baja, en contradicción con la Segunda Ley, tales estados representarían una ínfima minoría de las posibilidades. Puede decirse que éste es el «punto clave» de la noción de entropía y de la Segunda Ley. La definición de entropía de Boltzmann en términos de la noción de granulado grueso trata de una manera muy natural y adecuada esta cuestión del tipo de «especialidad» que es exigido por la baja entropía.

Otro punto es digno de mención aquí. Existe un teorema matemático clave, conocido como teorema de Liouville, que afirma que para el tipo normal de sistema dinámico clásico considerado por los físicos (los sistemas hamiltonianos estándar antes mencionados), la evolución temporal conserva los volúmenes en el espacio de fases. Esto se ilustra en la parte derecha de la Fig. 1.7, donde vemos que si una región de ₀, de volumen V en el espacio de fases , es transportada, al cabo de un tiempo t, por las curvas de evolución a una región _t, entonces encontramos que _t tiene el mismo volumen V que ₀. Sin embargo, esto no contradice la Segunda Ley, porque las regiones de grano grueso no son conservadas por la evolución. Si la región inicial ₀ resultaba ser una región de grano grueso, entonces sería probable que el volumen de _t fuera irregular y estuviera repartido en una región de grano grueso mucho mayor, o quizá en varias regiones semejantes, en un instante t posterior.

Para terminar esta sección, será apropiado volver a la importante cuestión del uso del logaritmo en la fórmula de Boltzmann, siguiendo algo que se ha abordado brevemente en §1.2. La cuestión tendrá una importancia particular para nosotros más adelante, muy especialmente en §3.4. Supongamos que estamos contemplando la física que tiene lugar en nuestro laboratorio local, y queremos considerar la definición de la entropía de algunas estructuras implicadas en un experimento que estamos realizando. ¿Cuál consideraríamos que es la definición de entropía de Boltzmann relevante para nuestro experimento? Tendríamos en cuenta todos los grados de libertad de interés, en el laboratorio, y los utilizaríamos para definir un espacio de fases . Dentro de estaría la región relevante de grano grueso de volumen V, que nos da nuestra entropía de Boltzmann klogV.

Sin embargo, podríamos considerar nuestro laboratorio como parte de un sistema mucho más grande, digamos que el resto de la galaxia Vía Láctea en la que residimos, donde hay muchísimos más grados de libertad. Al incluir todos estos grados de libertad, encontramos que nuestro espacio de fases será muchísimo mayor que antes. Además, la región de grano grueso pertinente para nuestro cálculo de entropías dentro de nuestro laboratorio también será muchísimo mayor que antes, porque puede incluir todos los grados de libertad presentes en toda la galaxia, y no sólo los relevantes para los contenidos del laboratorio. No obstante, esto es natural porque el valor de la entropía es ahora el que se aplica a la galaxia en conjunto, del que la entropía implicada en nuestro laboratorio es sólo una pequeña parte.

Los parámetros que definen los grados de libertad externos (los que determinan el estado de la galaxia excepto los que definen el estado dentro del laboratorio) nos ofrecen un inmenso espacio de fases «externo» , y habrá una región de grano grueso dentro de que caracteriza al estado de la galaxia externa al laboratorio. Véase la Fig. 1.9.

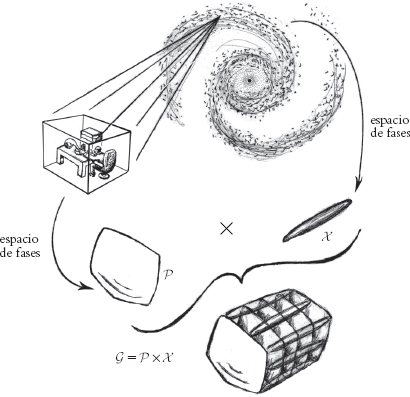
Fig. 1.9. El espacio de fases considerado por el experimentador no es sino un pequeño factor del que incluye todos los grados de libertad externos en la galaxia.

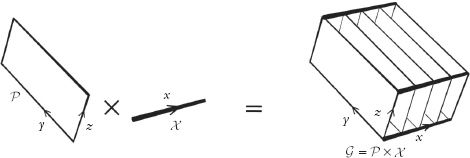
Fig. 1.10. Espacio producto donde es un plano y es una línea.

El espacio de fases para la galaxia entera estará definido por el conjunto completo de parámetros, tanto externos (que proporcionan el espacio ) como internos (que proporcionan el espacio ). El espacio es llamado por los matemáticos espacio producto^[1.4] de por , escrito

y su dimensión será la suma de las dimensiones de y de (porque sus coordenadas son las de seguidas de las de ). La Figura 1.10 ilustra la idea de un espacio producto, donde es un plano y es una línea.

Si consideramos que los grados de libertad externos son totalmente independientes de los internos, entonces la región de grano grueso relevante en será el producto

de las regiones de grano grueso en y en , respectivamente (véase la Fig. 1.11). Además, el elemento de volumen en un espacio producto es el producto de los elementos de volumen en cada uno de los espacios constituyentes; por consiguiente, el volumen de la región de grano grueso × en será el producto VW del volumen V de la región de grano grueso en por el volumen W de la región de grano grueso en . Entonces, por la propiedad «producto a suma» del logaritmo, la entropía de Boltzmann que obtenemos es

k log (VW) = k log V + k log W,

Fig. 1.11. Región de grano grueso en el espacio producto como un producto de regiones de grano grueso en los factores.

que es la suma de la entropía dentro del laboratorio y la entropía externa al laboratorio. Esto simplemente nos dice que las entropías de sistemas independientes se suman, lo que muestra que puede asignarse un valor de entropía a cualquier parte de un sistema físico que es independiente del resto del sistema.

En la situación aquí considerada en la que se refiere a los grados de libertad relevantes para el laboratorio y a los relevantes para la galaxia externa (que se suponen independientes unos de otros), encontramos que el valor de la entropía klogV que el experimentador asignaría al experimento que se está realizando, si se ignoran los grados de libertad externos, diferiría del valor de la entropía klog(VW) que resultaría si estos grados de libertad externos se toman también en consideración, simplemente en el valor de la entropía klogW que se asignaría a todos los grados de libertad galácticos externos. Esta parte externa no desempeña ningún papel para el experimentador y por consiguiente puede ser ignorada sin problemas para estudiar el papel de la Segunda Ley dentro del propio laboratorio. Sin embargo, cuando en §3.4 lleguemos a considerar el balance de entropía del universo en conjunto, y muy en particular la contribución debida a agujeros negros, encontraremos que estas materias no pueden ser ignoradas, ¡y adquirirán una importancia fundamental para nosotros!