1.1. La marcha implacable de la aleatoriedad

La Segunda Ley de la termodinámica… ¿cuál es esta ley? ¿Cuál es su papel fundamental en el comportamiento físico? ¿Y en qué sentido nos presenta un misterio auténticamente profundo? En las últimas secciones de este libro trataremos de entender la enigmática naturaleza de este misterio y por qué nos vemos impulsados a hacer todo lo posible por resolverlo. Esto nos llevará a áreas inexploradas de la cosmología, y a cuestiones que en mi opinión sólo pueden resolverse adoptando una perspectiva nueva y muy radical sobre la historia de nuestro universo. Pero éstas son cuestiones en las que nos interesaremos más tarde. Por el momento vamos a limitar nuestra atención a la tarea de entender lo que hay implicado en esta ubicua ley.

Normalmente, cuando pensamos en una «ley de la física» pensamos en un enunciado que afirma una igualdad entre dos cosas diferentes. La segunda ley de movimiento de Newton, por ejemplo, iguala la tasa de cambio del momento lineal (el producto de la masa por la velocidad) de una partícula a la fuerza total que actúa sobre la misma. Otro ejemplo es la ley de la conservación de la energía, que afirma que la energía total de un sistema aislado en un instante es igual a su energía total en cualquier otro instante. Análogamente, las leyes de conservación de la carga eléctrica, del momento lineal y del momento angular afirman una correspondiente igualdad para la carga eléctrica total, el momento lineal total y el momento angular total. La famosa ley de Einstein E = mc² afirma que la energía de un sistema es siempre igual a su masa multiplicada por el cuadrado de la velocidad de la luz. Y otro ejemplo más: la tercera ley de Newton afirma que la fuerza ejercida por un cuerpo A sobre un cuerpo B, en cualquier instante, es siempre igual y opuesta a la fuerza que actúa sobre A debida a B. Y lo mismo sucede con otras muchas leyes de la física.

Todas éstas son igualdades; y esto se aplica también a la llamada Primera Ley de la termodinámica, que en realidad es otra vez la ley de conservación de la energía, aunque ahora en un contexto termodinámico. Decimos «termodinámico» porque ahora se tiene en cuenta la energía de los movimientos térmicos, es decir, la energía de los movimientos aleatorios de las partículas constituyentes individuales. Esta energía es la energía térmica del sistema; la temperatura del sistema se define como dicha energía por grado de libertad (como consideraré de nuevo más adelante). Por ejemplo, cuando la fricción con el aire frena un proyectil, esto no viola la ley de conservación de la energía (esto es, la Primera Ley de la termodinámica); aunque el proyectil pierde energía cinética al frenarse, los movimientos aleatorios de las moléculas del aire, y las del proyectil, se hacen ligeramente más energéticos debido al calentamiento que produce la fricción.

Sin embargo, la Segunda Ley de la termodinámica no es una igualdad, sino una desigualdad que afirma simplemente que cierta magnitud conocida como la entropía de un sistema aislado —que es una medida del desorden, o «aleatoriedad», del sistema— es mayor (o al menos no menor) en instantes posteriores que lo era en instantes anteriores. Junto a esta aparente debilidad del enunciado, encontraremos que también hay cierta vaguedad o subjetividad en la propia definición de entropía de un sistema general. Más aún, en muchas formulaciones nos vemos llevados a concluir que hay momentos excepcionales u ocasionales en los que hay que considerar que la entropía realmente se reduce (aunque momentáneamente) con el tiempo (en una fluctuación) pese a que la tendencia general es hacia un aumento de la entropía.

Pero, frente a esta aparente imprecisión inherente en la Segunda Ley (como la llamaré de ahora en adelante para abreviar), esta ley tiene una universalidad que va mucho más allá de cualquier sistema particular de reglas dinámicas con las que se podría estar concernido. Es válida igualmente, por ejemplo, tanto para la teoría de la relatividad como para la teoría newtoniana, y asimismo para los campos continuos de la teoría del electromagnetismo de Maxwell (que trataré brevemente en §2.6, §3.1 y §3.2, y algo más explícitamente en el apéndice A1), así como también lo es para teorías que sólo incluyen partículas discretas. Es válida incluso para hipotéticas teorías dinámicas de las que no tenemos ninguna buena razón para creer que tengan relevancia para el universo real en el que habitamos. No obstante, su pertinencia queda más manifiesta cuando se trata con esquemas dinámicos realistas, tales como la mecánica newtoniana, que tienen una evolución determinista y son reversibles en el tiempo, de modo que para cualquier evolución admisible hacia el futuro la inversión de la dirección del tiempo nos da otra evolución igualmente admisible de acuerdo con el esquema dinámico.

Para decirlo en términos familiares: si tenemos una película que muestra una acción que está de acuerdo con leyes dinámicas —tales como las de Newton— que son reversibles en el tiempo, entonces la situación mostrada cuando la película se pasa al revés también estará de acuerdo con dichas leyes dinámicas. El lector podría sentirse intrigado por esto, pues mientras que una película que muestra un huevo que rueda por una mesa, cae al suelo y se aplasta representaría un proceso dinámico admisible, la película pasada al revés (que muestra el huevo aplastado, originalmente un amasijo en el suelo, que se recompone milagrosamente a partir de los fragmentos de cáscara, con la yema y la albúmina uniéndose por separado hasta rodearse de la cáscara recompuesta, y luego salta a la mesa) no es algo que esperemos ver alguna vez en un proceso físico real (Fig. 1.1). Pero la dinámica newtoniana de cada partícula individual, con su respuesta acelerada (de acuerdo con la segunda ley de Newton) a todas las fuerzas que actúan sobre ella, y las reacciones elásticas implicadas en cualquier colisión entre las partículas constituyentes, es completamente reversible en el tiempo. Éste sería también el caso para el comportamiento refinado de partículas relativistas y mecanocuánticas, de acuerdo con los procedimientos estándar de la física moderna, aunque hay ciertas sutilezas que surgen de la física de agujeros negros de la relatividad general, y también de la mecánica cuántica, en las que no quiero entrar todavía. Algunas de estas sutilezas tendrán una importancia crucial para nosotros más adelante, y se considerarán especialmente en §3.4. Pero por el momento bastará una imagen totalmente newtoniana de las cosas.

Tenemos que acostumbrarnos al hecho de que las situaciones que se muestran pasando la película en ambas direcciones son compatibles con la dinámica newtoniana, pero la que muestra la autorrecomposición del huevo es incompatible con la Segunda Ley, y sería una secuencia de sucesos tan sumamente improbable que sencillamente podemos descartarla como posibilidad realista. Lo que la Segunda Ley establece realmente, hablando en términos generales, es que las cosas se hacen cada vez más «aleatorias». De modo que si fijamos una situación particular y luego dejamos que evolucione hacia el futuro de acuerdo con la dinámica, el sistema evolucionará hacia un estado de apariencia más aleatoria a medida que pasa el tiempo. Hablando en sentido estricto, no deberíamos decir que evolucionará hacia un estado de apariencia más aleatoria sino que, de acuerdo con lo que se ha dicho antes, es abrumadoramente probable que evolucione hacia tal estado más aleatorio. En la práctica cabe esperar que, de acuerdo con la Segunda Ley, las cosas se hagan cada vez más y más aleatorias con el paso del tiempo, aunque esto representa simplemente una aplastante probabilidad, y no una absoluta certeza.

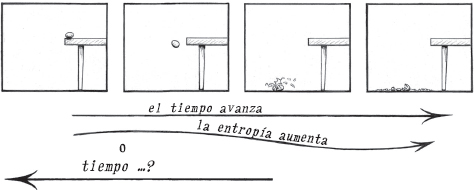
Fig. 1.1. Un huevo que rueda por una mesa, cae al suelo y se aplasta, de acuerdo con leyes dinámicas reversibles en el tiempo.

De todas formas podemos afirmar, con un extraordinario grado de confianza, que lo que experimentaremos será un aumento de entropía; en otras palabras, un aumento de aleatoriedad. Dicho así, la Segunda Ley suena quizá como una advertencia desesperada, pues nos dice que las cosas se están desorganizando cada vez más con el paso del tiempo. Esto no suena a misterio, sin embargo, como el título de la Parte 1 parece sugerir. Es sólo un aspecto obvio de cómo se comportarían las cosas si las dejamos a sí mismas. La Segunda Ley parece expresar una inevitable, y quizá deprimente, característica de la existencia cotidiana. De hecho, desde este punto de vista, la Segunda Ley de la termodinámica es una de las cosas más naturales imaginables y, por supuesto, algo que refleja una experiencia completamente común.

A algunos les podría preocupar que la emergencia de vida en esta Tierra, con su casi increíble sofisticación, represente una contradicción con este aumento del desorden que exige la Segunda Ley. Más tarde explicaré (véase §2.2) por qué no hay realmente contradicción. La biología es, hasta donde sabemos, totalmente compatible con el aumento de entropía global que exige la Segunda Ley. El misterio al que se refiere el título de esta Parte 1 es un misterio de la física en una escala de un orden totalmente diferente. Aunque guarda una relación precisa con esa misteriosa y enigmática organización que continuamente se nos manifiesta a través de la biología, tenemos buenas razones para esperar que esta última no presente ninguna paradoja con respecto a la Segunda Ley.

No obstante, una cosa debería quedar clara con respecto al estatus físico de la Segunda Ley: esta representa un principio independiente que debe ser añadido a las leyes dinámicas (por ejemplo, a las leyes de Newton), y no debe considerarse como algo que se deduce de ellas. La definición real de la entropía de un sistema en cualquier instante es, sin embargo, simétrica con respecto a la dirección del tiempo, de modo que obtenemos la misma definición de entropía, para nuestra película del huevo que cae, en cualquier instante, con independencia de la dirección en que se pase la película. Y si las leyes dinámicas son también simétricas en el tiempo (como sucede realmente con la dinámica newtoniana), y la entropía de un sistema no es siempre constante en el tiempo (como es tan evidente en el caso del huevo aplastado), entonces la Segunda Ley no puede ser una deducción de dichas leyes dinámicas. Pues si la entropía está aumentando en una situación particular (por ejemplo, el huevo que se aplasta), estando de acuerdo con la Segunda Ley, entonces la entropía debe estar disminuyendo en la situación invertida (el huevo que se recompone milagrosamente), lo que es una flagrante violación de la Segunda Ley. Puesto que aun así ambos procesos son compatibles con la dinámica (newtoniana), concluimos que la Segunda Ley no puede ser una consecuencia de las leyes dinámicas.