1.5. El inexorable aumento de la entropía en el futuro

Tratemos de entender por qué cabría esperar que la entropía aumente cuando el sistema evoluciona hacia el futuro, como exige la Segunda Ley. Imaginemos que nuestro sistema parte de un estado de entropía relativamente baja, de modo que el punto p que se va a mover en el espacio de fases describiendo con ello la evolución temporal del sistema, parte de un punto p₀ en una región de grano grueso bastante pequeña ₀ (véase la Fig. 1.15). Debemos tener en cuenta que, como ya se ha señalado, los tamaños de las diferentes regiones de grano grueso suelen diferir en factores absolutamente enormes. Además, la enorme dimensionalidad del espacio de fases tenderá a implicar que probablemente haya números enormes de volúmenes de grano grueso vecinos a cualquier región concreta. (Nuestras imágenes 2- o 3-dimensionales son más bien engañosas a este respecto, pero veremos que el número de vecinos aumenta con el aumento de la dimensión —típicamente seis en el caso 2-dimensional y catorce en 3 dimensiones; véase la Fig. 1.16)—. Así, será extraordinariamente probable que la curva de evolución descrita por p, cuando deja la región de grano grueso ₀ del punto de partida p₀ y entra en la siguiente región de grano grueso ₁, encuentre que ₁ tiene un volumen enormemente mayor que ₀; pues encontrar, en su lugar, un volumen enormemente menor parecería una acción muy improbable para el punto p, algo parecido a que p lograra, simplemente por azar, encontrar la proverbial aguja en un pajar, ¡pero aquí en una tarea aún más formidable!

Por consiguiente, el logaritmo del volumen de ₁ también será algo mayor que el logaritmo del volumen de ₀, aunque sólo modestamente mayor en comparación con lo que es el aumento en volumen real (véase §1.2 anterior), de modo que la entropía sólo habrá aumentado un poco. Luego, cuando p entra en la siguiente región de grano grueso, digamos ₂, es una vez más altamente probable encontrar que el volumen de ₂ es enormemente mayor que el de ₁, de modo que el valor de la entropía de nuevo crecerá algo. Esperamos entonces que p entre luego en otra región, digamos ₃, aun enormemente mayor que las regiones en las que ya había estado antes, y la entropía vuelve a aumentar algo, y así sucesivamente. Además, debido a los grandes aumentos en los volúmenes de estas regiones de grano grueso, una vez que p ha entrado en una región mayor podemos considerar una imposibilidad práctica —es decir, «abrumadoramente improbable»— que encuentre de nuevo una región menor, del tipo de regiones de tamaños mucho más minúsculos que proporcionarían valores de la entropía algo menores que los que se encontraron antes. Así, cuando el tiempo avanza hacia el futuro cabe esperar que el valor de la entropía aumente incesantemente, aunque mucho más modestamente que lo hacen los volúmenes reales.

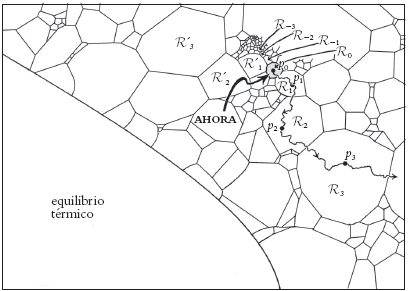
Fig. 1.15. El sistema parte de un punto p₀ en una pequeña región de grano grueso ₀.

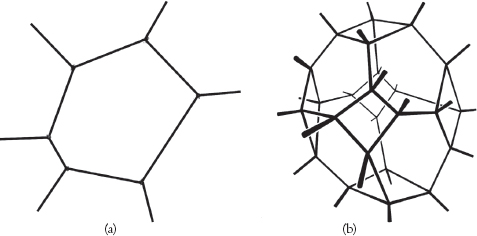
Fig. 1.16. Conforme aumenta la dimensión n, el número típico de regiones de grano grueso vecinas aumenta rápidamente. (a) n = 2 con típicamente 6 vecinos. (b) n = 3 con típicamente 14 vecinos.

Por supuesto, no es estrictamente imposible que de esta manera pueda obtenerse un valor menor de la entropía; lo que ocurre sencillamente es que tales casos de reducción de entropía deben considerarse abrumadoramente improbables. El aumento de la entropía que hemos obtenido es simplemente el tipo de tendencia que debemos considerar como estado de cosas normal, en el que la evolución procede de un modo que no tiene ningún sesgo particular con respecto al granulado grueso del espacio de fases; y también podría tratarse como si el camino de p a través del espacio de fases fuera esencialmente aleatorio, pese al hecho de que la evolución está realmente gobernada por los procedimientos bien definidos y totalmente deterministas de (digamos) la mecánica newtoniana.

Cabría preguntarse legítimamente por qué p no entra directamente en _max, la (inmensamente) mayor de las regiones de grano grueso, en lugar de ir entrando secuencialmente en una sucesión de regiones de grano grueso cada vez mayores, como se ha descrito antes. Aquí, _max se refiere a lo que habitualmente se conoce como equilibrio térmico, donde sería probable que el volumen de _max superara el volumen de todas las demás regiones de grano grueso juntas. De hecho, cabe esperar que p llegue finalmente a _max, y cuando lo haga permanecerá, en general, en dicha región, con la muy ocasional excursión a una región menor (una fluctuación térmica). Pero hay que considerar que la curva de evolución describe una evolución continua, donde no es probable que el estado en un instante difiera mucho del estado en un instante inmediatamente anterior. Por consiguiente, sería probable que los volúmenes de grano grueso no difieran de sus vecinos en una cantidad tan enorme como la que supondría un salto directo a _max, pese a los enormes cambios en los volúmenes de grano grueso que encontraría la curva de evolución. No parecería probable que la entropía salte de golpe; más bien esperaríamos que alcance gradualmente valores cada vez mayores.

Todo esto parece ser bastante satisfactorio, y muy bien podría llevarnos a creer que un aumento gradual de la entropía en el futuro es una expectativa completamente natural que apenas necesita una reflexión más profunda, excepto quizá por detalles de rigor que podrían ser necesarios para satisfacer al matemático purista. El huevo, mencionado en la sección anterior, que parte en el instante AHORA, colocado en el borde de la mesa, tiene probablemente una evolución futura con aumento de entropía que sería compatible con su caída desde la mesa y aplastamiento en el suelo. Esto está en perfecto acuerdo con las simples consideraciones del gran aumento de los volúmenes del espacio de fases, como ya se ha señalado.

Sin embargo, planteemos una pregunta algo distinta de la del comportamiento futuro esperado del huevo. Preguntemos por el comportamiento pasado probable del huevo. Lo que ahora queremos saber es: ¿cuál es la manera más probable de que el huevo haya llegado a encontrarse en el borde de la mesa?

Intentemos abordar esta pregunta de la misma manera que antes, cuando preguntábamos por la evolución futura más probable de nuestro sistema partiendo de AHORA, pero esta vez estamos preguntando por la evolución pasada más probable de nuestro sistema llegando a AHORA. Nuestras leyes newtonianas operan igualmente bien en la dirección del tiempo pasado, y de nuevo nos dan una evolución pasada determinista. Entonces hay una curva de evolución que lleva al punto p₀ del espacio de fases , que describe esta evolución pasada, y representa la manera en que el huevo llegó a estar colocado en el borde de la mesa. Para encontrar esta historia pasada «más probable» del huevo, examinamos de nuevo las regiones de grano hueso vecinas de ₀, y observamos de nuevo que hay grandes diferencias en sus tamaños. Por consiguiente, habrá muchísimas más curvas de evolución con final en p₀ que entran en ₀ desde una enorme región como ₁, cuyo volumen supera con mucho al de ₀, que curvas que entran en ₀ desde regiones mucho más pequeñas. Digamos que la curva de evolución entra en ₀ desde la región ₁′, mucho mayor que ₀. Antes de esto, habría de nuevo regiones vecinas de tamaños enormemente diferentes, y notamos de nuevo que la inmensa mayoría de evoluciones que entran en ₁′ procederían de regiones de grano grueso mucho mayores que ₁′. Por ello, parece que podemos suponer de nuevo que la curva de evolución pasada que entra en ₁′ procede de una región ₁′, de volumen enormemente mayor que ₁′, y que de la misma forma entró en ₂′ procedente de una región ₃′ de un volumen aún mayor que ₂′, y así sucesivamente.

Ésta es la conclusión a la que parece llevarnos nuestro razonamiento, pero ¿tiene sentido? Tales curvas de evolución serían enormemente más numerosas que las curvas de evolución que llegan a p₀ desde la sucesión de volúmenes mucho menores, digamos… ₋₃, ₋₂, ₋₁, ₀, lo que es probable que haya ocurrido realmente, cuyos volúmenes aumentarían enormemente a partir de volúmenes más pequeños, en la dirección del tiempo creciente, como sería compatible con la Segunda Ley. Más que ofrecernos un apoyo para la Segunda Ley, nuestra línea de razonamiento parece habernos llevado ahora a una respuesta completamente equivocada: ¡a esperar continuas violaciones flagrantes de la Segunda Ley en el pasado!

Nuestro razonamiento parece habernos llevado a esperar, por ejemplo, que una manera extraordinariamente probable de que nuestro huevo se encontrara originalmente colocado en el borde de la mesa es que empezó como un amasijo de cáscaras de huevo roto bajo la mesa, mezclado con yema y albúmina salpicados y parcialmente absorbidos en la alfombra. Luego este amasijo se recombinó de manera espontánea, saliendo limpiamente de la alfombra, con la yema y la albúmina claramente separadas y rodeadas por completo por la cáscara del huevo milagrosamente recompuesta para dar un huevo perfectamente construido, que se autoimpulsa desde el suelo a la velocidad correcta para que pueda posarse con delicadeza en el borde de la mesa. Tal comportamiento sería del tipo al que nos llevaba nuestro razonamiento anterior, con una curva de evolución «probable» que pasa sucesivamente por regiones de tamaños cada vez más reducidos, como …, ₃′, ₂′, ₁′, ₀. Pero esto estaría en fuerte conflicto con lo que presumiblemente sucedió en realidad, a saber: que alguna persona descuidada colocó el huevo en la mesa, sin darse cuenta de que corría el riesgo de rodar demasiado cerca del borde. Dicha evolución habría sido compatible con la Segunda Ley, estando representada en el espacio de fases por una curva de evolución que atraviesa la sucesión de volúmenes que aumentan enormemente …, ₋₃, ₋₂, ₋₁, ₀. Cuando se aplica en la dirección del tiempo pasado, nuestro argumento nos ha dado una respuesta que es lo más equivocada que podríamos imaginar.