1.4. El carácter robusto del concepto de entropía

Las cuestiones concernientes a la entropía del cosmos entero pueden dejarse al margen por ahora. Por el momento podemos limitarnos a apreciar el valor de la fórmula de Boltzmann, pues nos proporciona una excelente noción de cómo debería definirse realmente la entropía de un sistema físico. Boltzmann propuso esta definición en 1875, lo que representó un enorme avance respecto a lo que se había hecho hasta entonces;^[1.5] ahora se hace posible aplicar el concepto de entropía en situaciones completamente generales donde no es necesaria ninguna hipótesis especial, tal como que el sistema en cuestión tenga que estar en algún tipo de estado estacionario. Sin embargo, sigue habiendo cierta vaguedad en esta definición, asociada principalmente con lo que se entiende por un «parámetro macroscópico». Por ejemplo, podríamos imaginar que en el futuro será posible medir muchos aspectos detallados del estado de un fluido que hoy se consideran «inmedibles». Más que ser simplemente capaces de determinar, digamos, cuáles podrían ser la presión, densidad, temperatura y velocidad del flujo en varias localizaciones del fluido, quizá sea posible en el futuro determinar los movimientos de las moléculas del fluido con mucho más detalle, incluso medir los movimientos de moléculas específicas. Para ello habría que hacer un granulado grueso del espacio de fases bastante más fino que el que se había hecho antes. Por consiguiente, a la luz de esta tecnología más nueva la entropía de un estado particular del fluido se consideraría algo menor de lo que se hubiera considerado antes.

Algunos científicos han argumentado^[1.6] que el uso de esta tecnología para determinar detalles más finos de un sistema entrañaría siempre un aumento de entropía en el aparato de medida que compensaría con creces la reducción de entropía efectiva que, mediante medidas detalladas, podría determinarse que estaba teniendo lugar en el sistema bajo examen. Por consiguiente, dicha medida detallada de un sistema seguiría dando como resultado un aumento de la entropía total. Éste es un argumento muy razonable, pero incluso si lo tenemos en cuenta sigue habiendo algo turbio en la definición de entropía de Boltzmann, pues la falta de objetividad en lo que constituye un «parámetro macroscópico» para el sistema en conjunto apenas queda aclarada por tales consideraciones.

Un ejemplo extremo de este tipo de cosas fue ideado por el gran físico matemático del siglo XIX James Clerk Maxwell (cuyas ecuaciones para el electromagnetismo ya se han mencionado; §1.1 y §1.3). Maxwell imaginó un «demonio» minúsculo que, abriendo o cerrando una portezuela, era capaz de dirigir a cada molécula del gas en un sentido u otro, haciendo con ello que se violara la Segunda Ley aplicada al propio gas. Pero para considerar el sistema entero, incluido el cuerpo del propio demonio de Maxwell, como una única entidad física, habría que introducir en la imagen la composición submicroscópica real del demonio, y la Segunda Ley debería quedar restaurada una vez que se hace esto.

En términos más realistas podríamos imaginar que el demonio se reemplaza por un minúsculo artefacto mecánico, y podemos argumentar que la Segunda Ley sigue siendo válida para la estructura entera. Sin embargo, no me parece que la cuestión de lo que constituye un parámetro macroscópico quede adecuadamente resuelta por estas consideraciones, y la definición misma de entropía, para un sistema tan complicado, sigue siendo algo enigmática. Parece extraño que una magnitud física aparentemente bien definida como la entropía de un fluido ¡fuera dependiente del estado específico de la tecnología en cada momento!

Pese a todo, es notable lo poco que se verían afectados, en general, los valores de la entropía asignados a un sistema por tales desarrollos en la tecnología. Los valores de la entropía que se asignarían a un sistema, en conjunto, cambiarían muy poco como resultado de redibujar de esta manera las fronteras de las regiones de grano grueso, como podría resultar de una tecnología mejorada. Debemos tener en cuenta que probablemente habrá siempre algún grado de subjetividad en el valor preciso de la entropía que se podría asignar a un sistema a cuenta de la precisión de los aparatos de medida disponibles en cada momento, pero no por ello deberíamos adoptar el punto de vista de que la entropía no es un concepto físicamente útil. En la práctica, esta subjetividad se traducirá, en circunstancias normales, en un factor muy pequeño. La razón para ello es que las regiones de grano grueso suelen tener volúmenes que son desmesuradamente diferentes unos de otros, y el retrazado detallado de sus fronteras no supondrá normalmente ninguna diferencia discernible en los valores asignados de la entropía.

Para hacernos una idea de esto, volvamos a nuestra descripción simplificada de la mezcla de pintura roja y azul, que modelábamos considerando 10²⁴ compartimentos ocupados por iguales números totales de bolas rojas y azules. Allí considerábamos que el color en las diversas localizaciones era púrpura si la razón de bolas rojas a bolas azules en una gran caja cúbica 10⁵ × 10⁵ × 10⁵ yace en el rango 0,999 a 1,001. Supongamos que, en su lugar, gracias al uso de instrumentos más precisos, somos capaces de estimar la razón rojo/azul de las bolas en una escala mucho más fina que antes, y de forma mucho más precisa. Supongamos que ahora la mezcla se estima uniforme sólo si la razón de bolas rojas a bolas azules está entre 0,9999 y 1,0001 (de modo que los números de bolas rojas y azules van a ser ahora iguales con una precisión de una centésima de 1 por ciento), que es diez veces más precisa que la que exigíamos antes; y que la región examinada sólo necesita ahora ser la mitad de la dimensión lineal —y por consiguiente un octavo del volumen— que hubiéramos tenido que examinar antes para determinar el matiz. Pese a este considerable aumento de la precisión, encontramos que la «entropía» que debemos asignar a nuestro estado «púrpura uniforme» («entropía» en el sentido del logaritmo del número de estados que satisfacen ahora esta condición) apenas cambia respecto al valor que teníamos antes. Por consiguiente, nuestra «tecnología mejorada» no supone de hecho ninguna diferencia para el tipo de valores de la entropía que obtenemos en una situación de este tipo.

Éste es sólo un «modelo de juguete» (y un modelo de juguete del espacio de configuración antes que del espacio de fases), pero sirve para resaltar el hecho de que tales cambios en la precisión de nuestros «parámetros macroscópicos» en la definición de nuestras regiones de grano grueso no suelen suponer mucha diferencia en los valores asignados de la entropía. La razón básica para este carácter robusto de la entropía es simplemente el enorme tamaño de las regiones de grano grueso que encontramos y, más en particular, el enorme valor de las razones de los tamaños de tales regiones diferentes. Para tomar una situación más realista podríamos considerar el aumento de entropía implicado ¡en el acto común de tomar un baño! Por simplicidad no intentaré hacer una estimación del nada despreciable aumento de la entropía que se da en el proceso de limpieza real (!), sino que me concentraré sólo en lo que está implicado en la mezcla del agua que sale de los grifos frío y caliente (ya sea en la propia bañera o en el interior de un grifo mezclador que podría estar unido a la bañera). Sería razonable suponer que el agua caliente sale a una temperatura de unos 50 °C, y la fría a alrededor de 10 °C, y que el volumen total del agua que se acumula en la bañera es de unos 150 litros (la mitad de ellos de agua caliente y la otra mitad de agua fría). El aumento de la entropía resulta ser de unos 21407 J/K, lo que equivale a que nuestro punto del espacio de fases se mueva desde una región de grano grueso a otra que es ¡unas 10²⁷ veces más grande! Ningún cambio razonable en el trazado de las fronteras de las regiones de grano grueso debería suponer un cambio significativo en números de esta magnitud.

Habría que mencionar aquí otra cuestión relacionada. He expresado las cosas como si las regiones de grano grueso estuvieran bien definidas, con fronteras precisas, cuando en sentido estricto no sería así, independientemente de qué familia plausible de «parámetros macroscópicos» pudiera adoptarse. De hecho, trazáramos donde trazáramos la frontera de una región de grano grueso, dos puntos muy próximos en el espacio de fases, aunque estuvieran uno a cada lado de la frontera, representarían estados que son casi idénticos, y por consiguiente macroscópicamente idénticos; ¡y, pese a todo, se han juzgado «macroscópicamente distinguibles» en virtud de su pertenencia a diferentes regiones de grano grueso!^[1.7] Podemos solucionar este problema pidiendo que haya una región de «borrosidad» en las fronteras que separan cada región de grano grueso de las regiones adyacentes y, como sucedía con la cuestión de la subjetividad acerca de qué es exactamente lo que debe considerarse como «parámetro macroscópico», podemos simplemente decidir no preocuparnos de lo que hacemos con los puntos en el espacio de fases que yacen dentro de esta «frontera borrosa» (véase la Fig. 1.12). Es razonable considerar que tales puntos ocupan un volumen del espacio de fases muy pequeño en comparación con los enormes interiores de estas regiones de grano grueso. Por esta razón, considerar que un punto próximo a la frontera pertenece a una región o a otra será algo intranscendente, pues de hecho no supone ninguna diferencia para el valor de la entropía que normalmente se asignaría a un estado. De nuevo, encontramos que la noción de la entropía de un sistema es muy robusta —pese a cierta vaguedad en su definición— debido a la misma inmensidad de las regiones de grano grueso y el enorme desequilibrio entre sus tamaños.

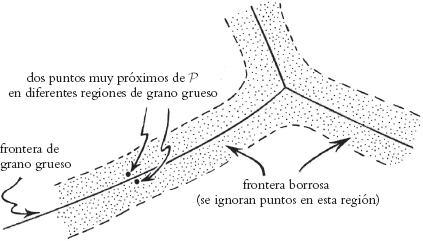
Fig. 1.12. «Borrosidad» en las fronteras que separan una región de grano grueso de las adyacentes.

Una vez dicho todo esto, hay que señalar, no obstante, que existen varias situaciones particularmente sutiles para las que estas crudas nociones de «indistinguibilidad macroscópica» parecerían inadecuadas, ¡hasta el punto de que parecen darnos respuestas muy equivocadas para la entropía! Una situación semejante se da en el fenómeno de ecos de espín (advertido por primera vez por Erwin Hahn en 1950) del que se hace uso en relación con la resonancia magnética nuclear (RMN). Según este fenómeno, un material con un estado específico inicial de magnetización, con espines nucleares^[1.8] perfectamente alineados, puede perder esta magnetización bajo la influencia de un campo electromagnético externo variable, y los espines nucleares adoptan entonces una configuración de una apariencia mucho más desordenada debido a una complicada serie de precesiones de espín que ocurren a ritmos diferentes. Pero si luego se invierte con cuidado el campo externo, todos los espines nucleares vuelven a sus estados originales, de modo que, sorprendentemente, ¡se recupera el estado original de magnetización! Si se consideran medidas macroscópicas parecería que la entropía había aumentado en la transición a esta etapa intermedia (con los espines nucleares desordenados) —de acuerdo con la Segunda Ley—, pero cuando, como resultado de la aplicación del campo electromagnético externo invertido, los espines nucleares recuperan el orden que habían perdido en la etapa intermedia, ¡parecería que ha habido una flagrante violación de la Segunda Ley, debida a una disminución de la entropía durante este proceso final!^[1.9]

El hecho es que incluso si los estados de espín parecían estar muy desordenados en la situación intermedia, hay realmente un «orden oculto» muy preciso en la disposición de espines aparentemente desordenados, orden que sólo se revela cuando se invierte la pauta de variaciones del campo magnético externo. Algo análogo ocurre con un disco CD o DVD, donde probablemente una cruda «medida macroscópica» ordinaria no revelaría la muy considerable información almacenada en dicho disco, mientras que un aparato de reproducción adecuado, específicamente diseñado para leer el disco, no tendría problemas en revelar esta información almacenada. Para detectar este orden oculto se necesitan medidas de un tipo mucho más sofisticado que las medidas macroscópicas «ordinarias» que serían adecuadas en la mayoría de las situaciones.

En realidad no tenemos necesidad de considerar algo tan técnicamente sofisticado como el examen de minúsculos campos magnéticos para encontrar «orden oculto» de este tipo general. Algo esencialmente similar ocurre con un aparato de apariencia mucho más simple (véase la Fig. 1.13, y la nota ^[1.10] para más información). Este consiste en dos tubos de vidrio cilíndricos, uno de los cuales encaja perfectamente dentro del otro, dejando un espacio muy estrecho entre ambos. Una manivela añadida al tubo interno permite rotarlo con respecto al externo, que permanece fijo. En este fino espacio entre los dos cilindros se introduce uniformemente un fluido viscoso (por ejemplo, glicerina). Ahora se monta el experimento de modo que inicialmente hay una fina línea recta de colorante rojo brillante insertada en el fluido, paralela al eje del cilindro (véase la Fig. 1.14). Entonces se le da varias vueltas a la manivela, a consecuencia de lo cual la línea de colorante se dispersa, hasta que se observa que está uniformemente distribuida alrededor del cilindro de modo que ya no se ve ninguna traza de su concentración original a lo largo del fluido, sino que el fluido adquiere un tono rosáceo muy tenue. Para cualquier elección razonable de «parámetros macroscópicos» para determinar el estado del fluido viscoso tintado, la entropía parecería haber aumentado, pues ahora la tinta está uniformemente dispersa sobre el fluido. (Podría parecer que la situación es muy similar a lo que sucedía con la mezcla agitada de pintura roja y azul que se ha considerado en §1.2). Sin embargo, si ahora se rota la manivela en la dirección contraria, con el mismo número de vueltas que se habían dado antes, encontramos, de forma casi milagrosa, que reaparece la línea de tinta roja y llega a hacerse casi tan claramente definida como lo estaba inicialmente. Si la entropía hubiera aumentado realmente en el giro de manivela inicial, en la cantidad que había parecido hacerlo, y si se considera que la entropía ha vuelto a casi su valor original después del giro inverso de la manivela, entonces ¡tenemos una clara violación de la Segunda Ley como resultado de este proceso de giro invertido!

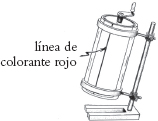
Fig. 1.13. Dos tubos de vidrio bien encajados con un fluido viscoso entre ambos, con una línea de colorante rojo.

En ambas situaciones, un punto de vista habitual es decir que la Segunda Ley no se ha violado en realidad, sino que en tales situaciones la definición de entropía no ha sido suficientemente refinada. En mi opinión, hay aquí una fuente de problemas si se exige que haya una definición precisa y objetiva de entropía física, aplicable en todas circunstancias, con respecto a la cual la Segunda Ley sea universalmente válida.

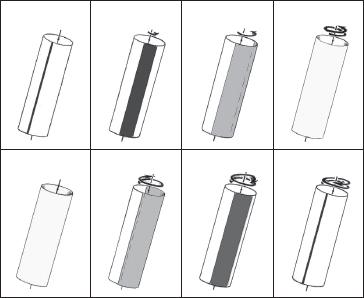
Fig. 1.14. Se dan varias vueltas a la manivela, lo que difunde la línea de colorante. Luego se da el mismo número de vueltas a la manivela en sentido contrario y la línea reaparece en aparente violación de la Segunda Ley.

No veo por qué habría que exigir que haya siempre una noción de entropía bien definida y físicamente precisa, que sea por completo objetiva y en consecuencia esté «ahí fuera» en la naturaleza en un sentido absoluto ^[1.11], y que esta entropía objetiva casi nunca disminuya con el paso del tiempo. ¿Debe haber siempre un concepto de entropía real que se aplica al fluido viscoso ligeramente coloreado entre los cilindros, o a las configuraciones de espines nucleares que habían parecido hacerse totalmente desordenadas, aunque reteniendo una memoria precisa del «orden» que habían tenido antes? No creo que haya esta necesidad. Sin duda la entropía es un concepto físico extraordinariamente útil, pero no veo por qué haya que asignarle un papel fundamental y verdaderamente objetivo en física. De hecho, me parece razonable que la utilidad de la noción física de entropía tiene su origen básicamente en el hecho de que, para sistemas que solemos encontrar en el universo real, las medidas normales de magnitudes «macroscópicas» dan lugar a volúmenes de grano grueso que difieren entre sí en factores inmensamente grandes. Sin embargo, hay una cuestión profunda y es por qué, en el universo que conocemos, deberían diferir en valores tan enormes. Estos factores enormes revelan un hecho notable sobre nuestro universo, que sí parece ser claramente objetivo y estar «ahí fuera» —y pronto llegaré a esto— pese a las cuestiones decididamente confusas de subjetividad que están implicadas en nuestro concepto de «entropía», que sólo sirven para nublar el misterio central que subyace en la profunda utilidad de esta notable noción física.