2.1. Nuestro universo en expansión.

El Big Bang: ¿qué creemos que sucedió realmente? ¿Hay clara evidencia observacional de que realmente tuvo lugar una explosión primordial, de la que parece haberse originado todo el universo que conocemos? Y una pregunta fundamental para las cuestiones planteadas en la Parte 1: ¿cómo un suceso tan increíblemente violento y tórrido puede representar un estado de entropía extraordinariamente minúscula?

Inicialmente, la razón principal para creer en un origen explosivo del universo provino de las persuasivas observaciones del astrónomo estadounidense Edwin Hubble, que mostraban que el universo se está expandiendo. Esto fue en 1929, aunque indicios de esta expansión ya habían sido advertidos por Vesto Slipher en 1917. Las observaciones de Hubble demostraban de forma bastante convincente que las galaxias lejanas se están alejando de nosotros a velocidades que son básicamente proporcionales a sus distancias a nosotros, de modo que si extrapolamos hacia atrás, llegamos a la conclusión de que todas las cosas habrían estado juntas más o menos al mismo tiempo. Este suceso habría constituido una tremenda explosión —que ahora llamamos «Big Bang»— en la que toda la materia parece haber tenido su origen último. Observaciones posteriores, de las que hay muchas, y experimentos específicos detallados (a algunos de los cuales llegaré en breve), han confirmado y reforzado enormemente las conclusiones iniciales de Hubble.

Las consideraciones de Hubble se basaban en la observación de un desplazamiento hacia el rojo de las líneas espectrales en la luz emitida por galaxias lejanas. El término «desplazamiento hacia el rojo» se refiere al hecho de que el espectro de las frecuencias emitidas por diferentes tipos de átomos en una galaxia lejana se ve, desde la Tierra, ligeramente desplazado en la dirección del rojo (Fig. 2.1), lo que supone una reducción uniforme en la frecuencia que puede interpretarse como un desplazamiento Doppler,^[2.1] es decir, un enrojecimiento debido a que el objeto observado se aleja de nosotros a una velocidad considerable. El desplazamiento hacia el rojo es mayor para las galaxias que parecen estar más lejanas, y la correlación con la distancia aparente resulta ser compatible con la imagen de Hubble de una expansión espacialmente uniforme del universo.

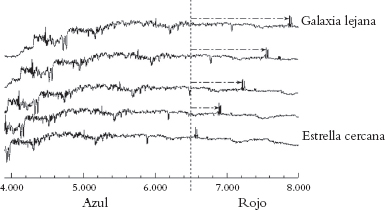
Fig. 2.1. El «desplazamiento hacia el rojo» del espectro emitido por los átomos en una galaxia lejana es compatible con una interpretación como un desplazamiento Doppler.

En años posteriores se han producido muchos refinamientos en las observaciones y en su interpretación, y es justo decir que no sólo la sugerencia original de Hubble ha sido confirmada, en términos generales, sino que trabajos recientes han dado una visión bastante detallada de cómo ha evolucionado en el tiempo el ritmo de expansión del universo, lo que nos ofrece una imagen que es hoy día generalmente aceptada (aunque todavía hay algunas destacadas voces disidentes,^[2.2] cuando se llega a algunos detalles). En particular, hay un acuerdo general en fijar una fecha de hace 1,37 × 10¹⁰ años para el momento en que toda la materia del universo habría tenido que estar concentrada en su punto de partida, a lo que nos referimos como «Big Bang».^[2.3]

No hay que pensar en el Big Bang como algo localizado en una región particular del espacio. La visión que adoptan los cosmólogos, de acuerdo con la perspectiva de la relatividad general de Einstein, es que en el instante que ocurrió, el Big Bang englobaba toda la extensión espacial del universo, de modo que incluía la totalidad del espacio físico, y no meramente el contenido material del universo. Por ello, se considera que el propio espacio era, en un sentido adecuado, muy minúsculo en dicho instante. Para entender estas cuestiones desconcertantes es necesario tener alguna idea de cómo funciona el espacio curvo en la teoría de la relatividad de Einstein. En §2.2 abordaré la teoría de Einstein de un modo bastante serio, pero por el momento nos contentaremos con una analogía que se utiliza con frecuencia, a saber, la de un globo que se hincha. El universo, como la superficie del globo, se expande con el tiempo, pero la totalidad del espacio se expande con él, sin que haya ningún punto central en el universo a partir del cual todo se expande. Por supuesto, el espacio 3-dimensional en el globo se expande si contiene un punto en su interior que es un centro para la superficie del globo, pero este punto no es parte de la superficie del globo, y es esta superficie la que se considera que representa la totalidad de la geometría espacial del universo.

La dependencia temporal de la expansión del universo real, tal como revelan las observaciones, está en sorprendente acuerdo con las ecuaciones de la teoría de la relatividad general de Einstein, pero al parecer sólo si se incorporan en la teoría dos ingredientes algo inesperados, ahora comúnmente conocidos bajo los nombres (algo desafortunados)^[2.4] de «materia oscura» y «energía oscura». Estos dos ingredientes tendrán una importancia considerable para el esquema de cosas que presentaré al lector a su debido tiempo (véanse §3.1 y §3.2). Ahora son parte de la imagen estándar de la cosmología moderna, pero hay que decir que ninguno de ellos es completamente aceptado por todos los expertos en el campo.^[2.5] Por mi parte, no tengo problemas en aceptar la presencia de algún material invisible —la «materia oscura»— de una naturaleza esencialmente desconocida para nosotros, pese a que constituye alrededor del 70 por ciento de la sustancia material de nuestro universo, y también que las ecuaciones de Einstein de la relatividad general deben tomarse en una forma modificada que él mismo presentó en 1917 (aunque más tarde se retractó), en la que hay que incorporar una minúscula constante cosmológica positiva Λ (la forma más plausible de «energía oscura»).

Habría que señalar que la teoría de la relatividad general de Einstein (con o sin la minúscula Λ) está ahora extraordinariamente bien comprobada en la escala del sistema solar. Incluso los muy prácticos sistemas de posicionamiento global, que ahora son de uso común, dependen de la relatividad general para su extraordinaria precisión. Mucho más impresionante es la extraordinaria precisión de la teoría de Einstein en su modelización del comportamiento de los sistemas de púlsares binarios, ^[2.6] que llega a ser de una parte en 10¹⁴ (en el sentido de que la secuencia temporal de las señales del púlsar procedentes del sistema binario PSR-1913 + 16, durante un período de unos cuarenta años, se modeliza exactamente con una precisión del orden de 10⁻⁶ segundos por año).

Los modelos cosmológicos originales, basados en la teoría de Einstein, eran los propuestos por el matemático ruso Alexander Friedmann en 1922 y 1924. En la Fig. 2.2 he esbozado las historias espaciotemporales de estos modelos, que muestran las evoluciones temporales de los tres casos (tomando Λ = 0) en los que la curvatura espacial del universo es, respectivamente, positiva, cero y negativa.^[2.7] El convenio que utilizaré en prácticamente todos mis diagramas espaciotemporales es que la dirección vertical representa la evolución temporal y las direcciones horizontales representan el espacio. En los tres casos se supone que la parte espacial de la geometría es completamente uniforme (lo que se denomina homogénea e isótropa). Los modelos cosmológicos con este tipo de simetrías se denominan modelos de Friedmann-Lemaître-Robertson-Walker (FLRW). Los modelos de Friedmann originales son un caso particular, en el que el tipo de materia que se está describiendo es un fluido sin presión, o «polvo» (véase también §2.4).

Fig. 2.2. Historias espaciotemporales para los modelos cosmológicos de Friedmann en los que la curvatura espacial del universo es positiva, cero y negativa (de izquierda a derecha).

En esencia,^[2.8] hay sólo tres casos a considerar para la geometría espacial, a saber, el caso K > 0 de curvatura espacial positiva, donde la geometría espacial es el equivalente 3-dimensional a una superficie esférica (como nuestro globo, antes mencionado), el caso plano K = 0, donde la geometría espacial es la familiar geometría 3-dimensional de Euclides, y el caso curvado negativamente K < 0 de 3-geometría espacial hiperbólica. Es una suerte para nosotros que el artista holandés Maurits C. Escher haya ilustrado estos tres tipos diferentes de geometría de forma muy bella en términos de teselaciones de ángeles y diablos; véase la Fig. 2.3. Debemos tener presente que estas teselaciones muestran simplemente una geometría espacial 2-dimensional, aunque también existen geometrías análogas a estos tres tipos de geometría en las 3 dimensiones espaciales.

Todos estos modelos empiezan con un estado «Big Bang» singular —donde «singular» se refiere al hecho de que la densidad de materia y la curvatura de la geometría espaciotemporal se hacen infinitas en este estado inicial—, de modo que las ecuaciones de Einstein (y la física, en general, tal como la conocemos) simplemente «se retiran» en la singularidad (aunque véase §3.2 y el apéndice B10). Se advertirá que el comportamiento temporal de estos modelos refleja bastante bien su comportamiento espacial. El caso espacialmente finito (K > 0; Fig. 2.3(a)) es también el caso temporalmente finito, donde no sólo hay una singularidad Big Bang inicial sino que también hay una final, comúnmente conocida como un «Big Crunch». Los otros dos casos (K < 0; Fig. 2.3 (b),(c)) no sólo son espacialmente infinitos,^[2.9] sino también temporalmente infinitos, pues su expansión continúa indefinidamente.

A partir de 1998, sin embargo, cuando dos grupos observacionales, uno encabezado por Saul Perlmutter y el otro por Brian P. Schmidt, analizaron sus datos concernientes a explosiones de supernovas muy lejanas,^[2.10] se han acumulado pruebas que indican con fuerza que la expansión del universo en sus últimas etapas no encaja realmente con los ritmos de evolución predichos por las cosmologías estándar de Friedmann que se ilustran en Fig. 2.2. En su lugar, parece que nuestro universo ha empezado a acelerar su expansión a un ritmo que se explicaría si incluimos en las ecuaciones de Einstein una constante cosmológica Λ, con un pequeño valor positivo. Estas observaciones, y otras posteriores de diversos tipos,^[2.11] han proporcionado pruebas bastante convincentes de los comienzos de la expansión exponencial característica de un modelo de Friedmann con Λ > 0. Esta expansión exponencial no sólo ocurre con los casos K ≤ 0, que en cualquier caso se expanden indefinidamente en sus futuros remotos incluso cuando Λ = 0, sino también en el caso espacialmente cerrado K > 0, con tal de que Λ sea lo bastante grande para superar la tendencia a recolapsar que tiene el modelo de Friedmann cerrado. De hecho, las observaciones indican la presencia de una Λ suficientemente grande, de modo que el valor (signo) de K se ha hecho más o menos irrelevante para el ritmo de expansión; el valor (positivo) de Λ que realmente parece estar presente en las ecuaciones de Einstein dominaría entonces el comportamiento tardío, lo que proporciona una expansión exponencial con independencia del valor de K dentro del rango observacionalmente aceptable. Por consiguiente, parece que tenemos un universo con un ritmo de expansión que básicamente está de acuerdo con la curva que se muestra en la Fig. 2.4, y la imagen espaciotemporal parece estar de acuerdo con la Fig. 2.5.

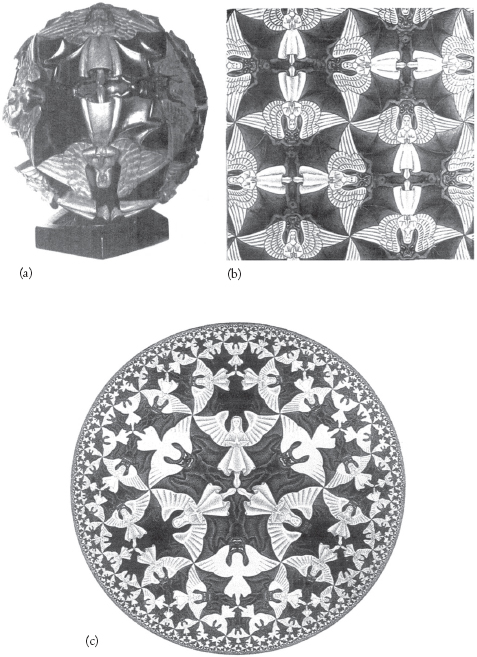
Fig. 2.3. Los tres tipos básicos de geometría plana uniforme ilustrados por Maurits C. Escher: (a) elíptica (positiva, K > 0); (b) euclidiana (plana, K = 0); hiperbólica (negativa, K < 0). Copyright M. C. Escher Company (2004).

En vista de ello, no me interesaré particularmente aquí en la diferencia entre estas tres posibilidades para la geometría espacial del universo. De hecho, las observaciones actuales indican una geometría espacial global para el universo que está muy próxima al caso plano K = 0. En cierto sentido esto es algo desafortunado, porque nos dice que no sabemos realmente la respuesta a la pregunta de cuál es probablemente la geometría espacial global del universo —por ejemplo, si el universo es espacialmente cerrado por necesidad, o si podría ser espacialmente infinito— porque en ausencia de poderosas razones teóricas para creer lo contrario, siempre quedará una posibilidad de una pequeña curvatura global positiva o negativa.

Fig. 2.4. Ritmo de expansión del universo para Λ positiva, con crecimiento exponencial final.

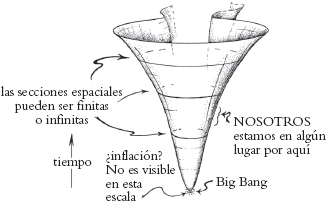
Fig. 2.5. Expansión espaciotemporal del universo. Imagen con Λ positiva (dibujada de forma que no esté sesgada con respecto al valor de K).

Por otra parte, muchos cosmólogos son de la opinión de que el punto de vista que proporciona la inflación cósmica ofrece una razón poderosa para creer que la geometría espacial del universo debe ser (salvo desviaciones locales relativamente pequeñas) realmente plana (K = 0), y por ello se muestran satisfechos con esta proximidad observacional a la planitud. La inflación cósmica es una propuesta que afirma que, dentro de un minúsculo período temporal en algún momento entre 10⁻³⁶ y 10⁻³² segundos después del Big Bang, el universo experimentó una expansión exponencial que incrementó su dimensión lineal en un factor enorme, de alrededor de 10³⁰ o 10⁶⁰ (o incluso 10¹⁰⁰) o así. Más adelante tendré más que decir sobre la inflación cósmica (véase §2.6), pero por el momento sólo debería advertir al lector que no siento entusiasmo por esta propuesta, pese a que goza de una aceptación casi universal entre los cosmólogos actuales. En cualquier caso, la presencia de una temprana etapa inflacionaria en la historia del universo no afectaría la apariencia de las Figs. 2.2 y 2.5, puesto que los efectos de la inflación se manifestarían sólo en las etapas muy tempranas, inmediatamente después del Big Bang, y no serían visibles en la escala en la que están dibujadas las Figs. 2.2 y 2.5. Por el contrario, las ideas que presentaré más adelante en este libro parecen ofrecer alternativas creíbles a la inflación para explicar esos fenómenos observados que parecen depender de ella en los esquemas cosmológicos actualmente más populares (véase §3.5).

Aparte de estas consideraciones, tengo una motivación muy diferente para presentar aquí la imagen de la Fig. 2.3(c), puesto que ilustra un punto que tendrá una importancia fundamental para nosotros más adelante. Este bello grabado de Escher se basa en una representación particular del plano hiperbólico, que es una de las varias representaciones propuestas por el muy ingenioso geómetra italiano Eugenio Beltrami ^[2.12] en 1868. La misma representación fue redescubierta más tarde, unos catorce años después, por el destacado matemático francés Henri Poincaré, cuyo nombre va asociado más habitualmente a ella. Para no añadir más confusión a la terminología, simplemente la llamaré representación conforme del plano hiperbólico, donde el término «conforme» se refiere al hecho de que en esta geometría los ángulos son correctamente representados en el plano euclidiano en el que se ha mostrado. Las ideas de la geometría conforme se abordarán con más detalle en §2.3.

Tenemos que considerar que todos los diablos en la geometría son mutuamente congruentes de acuerdo con la geometría hiperbólica que se está representando, y análogamente deben considerarse congruentes todos los ángeles. Evidentemente sus tamaños, según la medida euclidiana de fondo, se representan más pequeños cuanto más próximos a la frontera circular los examinamos, pero la representación de ángulos o formas infinitesimales sigue siendo válida, por muy cerca de la frontera que los examinemos. La propia frontera circular representa el infinito para esta geometría, y es esta representación conforme del infinito como una frontera finita suave la que estoy señalando al lector, pues desempeñará un papel central en las ideas a las que llegaré más adelante (particularmente en §2.5 y §3.2).