2.2. El ubicuo fondo de microondas

En la década de 1950 había una teoría del universo conocida como el modelo del estado estacionario, un modelo propuesto inicialmente por Thomas Gold y Hermann Bondi en 1948, y pronto asumido y elaborado con más detalle por Fred Hoyle;^[2.13] los tres estaban entonces en la Universidad de Cambridge. La teoría requería una continua creación de materia en todo el espacio, a un ritmo extraordinariamente lento. Esta materia tendría que estar en forma de átomos de hidrógeno —cada uno de los cuales consiste en un protón y un electrón, creados a partir del vacío— y el ritmo de creación tendría el valor extremadamente minúsculo de aproximadamente un átomo por metro cúbico cada mil millones de años. Éste sería el ritmo correcto para compensar la reducción de la densidad de materia debida a la expansión del universo.

En muchos aspectos, éste es un modelo estéticamente agradable y filosóficamente atractivo, pues el universo no requiere un origen en el tiempo ni en el espacio, y muchas de sus propiedades pueden deducirse del requisito de que debería ser autopropagante. Fue poco después de que fuera propuesta esta teoría cuando ingresé en la Universidad de Cambridge, en 1952, como joven estudiante de grado (que investigaba en matemáticas puras, pero con un fuerte interés en física y cosmología);^[2.14] más tarde, en 1956, regresé como investigador. Mientras estaba en Cambridge llegué a conocer a los tres proponentes originales de la teoría del estado estacionario, y este modelo me resultaba atractivo y sus argumentos muy convincentes. Sin embargo, hacia el final de mi estancia en Cambridge, recuentos detallados de galaxias lejanas llevados a cabo en el Radio Observatorio Mullard por (sir) Martin Ryle (también en Cambridge) estaban empezando a proporcionar evidencia observacional en contra del modelo del estado estacionario.^[2.15]

Pero el auténtico golpe mortal fue la observación accidental por parte de los estadounidenses Arno Penzias y Robert W. Wilson, en 1964, de una radiación electromagnética de microondas procedente de todas las direcciones del espacio. De hecho, tal radiación había sido predicha a finales de la década de 1940 por George Gamow, y por Robert Dicke, sobre la base de la que entonces era la más convencional «teoría del Big Bang». La radiación que se observa actualmente suele describirse como el «destello del Big Bang», que se ha enfriado desde los 4.000 K hasta unos pocos grados por encima del cero absoluto^[2.16] por un efecto de desplazamiento hacia el rojo debido a la enorme expansión del universo que ha tenido lugar desde el momento en que fue emitida la radiación. Una vez que Penzias y Wilson se convencieron de que la radiación que estaban observando (de aproximadamente 2,725 K) era auténtica, y realmente debía proceder del espacio profundo, se pusieron en contacto con Dicke, quien rápidamente les sugirió que sus enigmáticas observaciones podían ser explicadas por lo que él y Gamow habían predicho. Esta radiación ha recibido varios nombres diferentes («radiación reliquia», «fondo de 3 grados», etc.); hoy día se conoce normalmente como «CMB», iniciales de «Cosmic Microwave Background» (fondo cósmico de microondas).^[2.17] En 1978, Penzias y Wilson fueron galardonados con el Premio Nobel de Física por su descubrimiento.

Sin embargo, la fuente de los fotones que realmente constituyen el CMB que «vemos» ahora no es el «Big Bang real», pues estos fotones nos llegan directamente desde lo que se denomina la «superficie de última dispersión» que se dio unos 379.000 años después del momento del Big Bang (es decir, cuando el universo tenía aproximadamente 1/36.000 de su edad actual). Antes de eso el universo era opaco a la radiación electromagnética porque habría estado habitado por grandes números de partículas cargadas —principalmente protones y electrones— que pululaban separadas unas de otras, formando lo que se conoce como un «plasma». Los fotones habrían sido dispersados muchas veces por esta materia, siendo absorbidos y creados copiosamente, y el universo estaría muy lejos de ser transparente. Esta situación «neblinosa» habría continuado hasta el momento conocido como «desacoplamiento» (cuando ocurre la «última dispersión») en que el universo se hizo transparente porque se había enfriado lo suficiente para que los electrones y protones separados pudieran aparearse, básicamente en forma de hidrógeno. (También se produjeron algunos otros átomos, principalmente un 23 por ciento de helio, cuyos núcleos, llamados «partículas α», habrían estado entre los productos de los primeros pocos minutos de existencia del universo). Los fotones pudieron entonces desacoplarse de estos átomos neutros, y luego viajar esencialmente libres de perturbaciones para convertirse en la radiación que ahora percibimos como CMB.

Desde su observación inicial en la década de1960 se han realizado muchos experimentos para obtener datos cada vez mejores concernientes a la naturaleza y distribución del CMB. La información es ahora tan detallada que la disciplina de la cosmología se ha transformado por completo: de ser algo en lo que había mucha especulación y muy pocos datos para mantenerla, ha pasado a ser una ciencia de precisión, en la que, aunque sigue habiendo mucha especulación, ¡hay ahora gran cantidad de datos detallados para modular esta especulación! Un experimento particularmente digno de atención fue el del satélite COBE (Cosmic Background Explorer), lanzado por la NASA en noviembre de 1989. Sus notables observaciones les valieron a George Smoot y John Mather el Premio Nobel de Física de 2006.

Hay dos características muy importantes y sorprendentes del CMB que quedaron particularmente de manifiesto gracias a COBE, y voy a centrarme en ellas. La primera es la extraordinaria precisión con que el espectro de frecuencias observado encaja con el espectro explicado por Max Planck en 1900 para dar cuenta de la naturaleza de lo que se denomina «radiación de cuerpo negro» (que marcó el punto de partida de la mecánica cuántica). La segunda es la naturaleza extremadamente uniforme del CMB en todo el cielo. Cada uno de estos dos hechos nos estará diciendo algo muy fundamental sobre la naturaleza del Big Bang y su curiosa relación con la Segunda Ley. De esto ha salido buena parte de la cosmología moderna, que ahora está más interesada en las ligeras y sutiles desviaciones respecto de la uniformidad que también se ven en el CMB. Más tarde (véase §3.6) hablaré de éstas, pero por el momento tendré que abordar de uno en uno estos dos hechos más destacables, pues encontraremos que ambos tienen una gran importancia para nosotros.

La Fig. 2.6 muestra el espectro de frecuencias del CMB, esencialmente tal como fue medido por COBE, aunque con una mayor precisión que se ha obtenido ahora gracias a observaciones posteriores. El eje vertical mide la intensidad de la radiación, en función de las diferentes frecuencias, marcadas a lo largo del eje horizontal con la frecuencia aumentando hacia la derecha. La línea continua es la «curva de cuerpo negro» de Planck, que viene dada por una fórmula específica,^[2.18] y es la que la mecánica cuántica nos dice que corresponde al espectro de radiación de equilibrio térmico para una temperatura particular T. Las pequeñas barras verticales son barras de error, que nos dicen el rango aproximado dentro del que yacen las intensidades observadas. Habría que señalar, no obstante, que estas barras de error están exageradas en un factor 500, de modo que los puntos de las observaciones reales yacen mucho más cerca de la curva de Planck de lo que podría parecer; tan cerca, de hecho, que incluso las observaciones en el extremo derecho, donde el error es más grande, ¡se superponen a simple vista con la curva de Planck, dentro del grosor de la línea de tinta! De hecho, el CMB nos ofrece el acuerdo más preciso entre un espectro observado y la curva teórica de cuerpo negro de Planck que se conoce en la ciencia observacional.

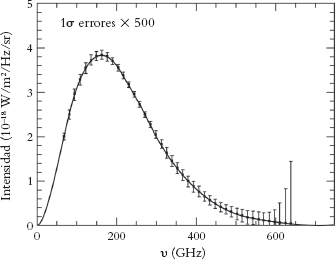
Fig. 2.6. Espectro de frecuencias del CMB, tal como fue observado inicialmente por COBE, pero complementado por observaciones posteriores más precisas. Nótese que las «barras de error» están exageradas en un factor de 500. Esto muestra un acuerdo muy preciso con el espectro de Planck.

¿Qué nos dice esto? Parece decirnos que lo que estamos mirando procede de un estado que debe estar efectivamente en equilibrio térmico. Pero ¿qué significa realmente «equilibrio térmico»? Remito al lector a la Fig. 1.15, donde encontramos las palabras «equilibrio térmico» etiquetando la región de grano grueso del espacio de fases que es (con mucho) la mayor de todas. En otras palabras, ésta es la región que representa la máxima entropía. Pero debemos recordar la fuerza de los argumentos que se han dado en §1.6. Esos argumentos nos decían que la base general de la Segunda Ley debe explicarse por el hecho de que el estado inicial del universo —que evidentemente debemos considerar que es el Big Bang— debe ser un estado (macroscópico) de entropía extraordinariamente minúscula. Lo que parece que hemos encontrado es, en esencia, todo lo contrario: ¡un estado (macroscópico) de máxima entropía!

Hay que abordar aquí un punto, a saber, el hecho de que el universo se está expandiendo, de modo que lo que estamos examinando difícilmente puede ser un estado de «equilibrio» real. Sin embargo, lo que claramente está sucediendo es una expansión adiabática, donde «adiabática» se refiere a un cambio «reversible» en el que la entropía permanece constante. El hecho de que este tipo de «estado térmico» se conserva realmente en la expansión del universo primitivo fue señalado por R. C. Tolman en 1934.^[2.19] Veremos algo más de las contribuciones de Tolman a la cosmología en §3.3. En términos del espacio de fases, la imagen de la Fig. 1.15 debe sustituirse por la de la Fig. 2.7, donde se describe la expansión como una sucesión de regiones de grano grueso maximales de volumen esencialmente igual. En este sentido, la expansión aún puede verse como un tipo de equilibrio térmico.

Así pues, parece que seguimos viendo máxima entropía. Al parecer, hay algo seriamente equivocado en este argumento. No se trata simplemente de que las observaciones del universo nos hayan dado una sorpresa. En absoluto: en cierto sentido, las observaciones están en estrecho acuerdo con lo que cabía esperar. Dado que realmente hubo un Big Bang, y que dicho estado inicial tiene que describirse de acuerdo con la imagen estándar que presenta la cosmología de la relatividad general, un estado térmico inicial muy caliente y uniforme es lo que cabría esperar. Entonces, ¿dónde está la solución a este enigma? Quizá, de forma bastante sorprendente, la cuestión tenga que ver con la hipótesis de que el universo está realmente en acuerdo con la imagen estándar de la cosmología relativista. Tendremos que examinar esta hipótesis con mucho cuidado, para ver qué se nos ha pasado por alto.

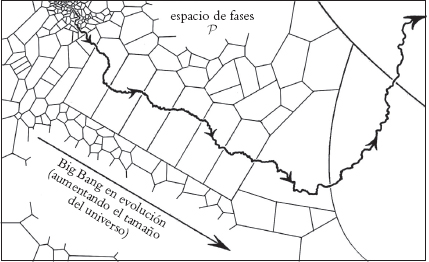
Fig. 2.7. Expansión adiabática del universo mostrada como una sucesión de regiones de grano grueso maximales de igual volumen.

En primer lugar, tenemos que recordarnos de qué trata la teoría de la relatividad general de Einstein. Es, después de todo, una teoría de la gravedad extraordinariamente precisa, en donde el campo gravitatorio se describe en términos de una curvatura del espacio-tiempo. Tendré mucho que decir sobre esta teoría a su debido tiempo, pero por el momento pensemos en términos de la más vieja —y todavía extraordinariamente precisa— teoría gravitatoria newtoniana, y tratemos de entender, en términos muy generales, cómo encaja con la Segunda Ley. (Me refiero, por supuesto, a la Segunda Ley de la termodinámica, y no a la segunda ley de Newton).

A menudo, las consideraciones de la Segunda Ley podrían discutirse en términos de un gas obligado a estar dentro de una caja cerrada. De acuerdo con estas discusiones, imaginemos que hay un pequeño compartimento en una esquina de la caja, y que el gas está inicialmente confinado dentro de dicho compartimento. Cuando se abre la puerta del compartimento y se permite que el gas se mueva libremente por la caja, esperamos que se difunda con rapidez de manera uniforme dentro de la caja, proceso en que la entropía aumentará de acuerdo con la Segunda Ley. La entropía es entonces mucho más alta para el estado macroscópico en que el gas está distribuido uniformemente que lo era cuando todo el gas estaba en el compartimento. Véase la Fig. 2.8(a). Pero consideremos ahora una situación en apariencia similar aunque con una caja imaginaria de tamaño galáctico, y en donde las moléculas de gas individuales se reemplazan por estrellas individuales que se mueven dentro de esta caja. La diferencia entre esta situación y la del gas no es sólo una cuestión de escala, y consideraré que el tamaño es irrelevante para nuestros objetivos presentes. Lo que es relevante es el hecho de que las estrellas se atraen mutuamente por la implacable fuerza de la gravedad. Podríamos imaginar que la distribución de estrellas es inicialmente bastante uniforme sobre nuestra caja de tamaño galáctico. Pero ahora, conforme avanza el tiempo, encontramos una tendencia de las estrellas a juntarse en grumos (y, en general, a moverse más rápidamente cuando lo hacen). Ahora la distribución uniforme no es la de entropía más alta, y el incremento de entropía se acompaña de un aumento en el carácter grumoso de la distribución. Véase la Fig. 2.8(b).

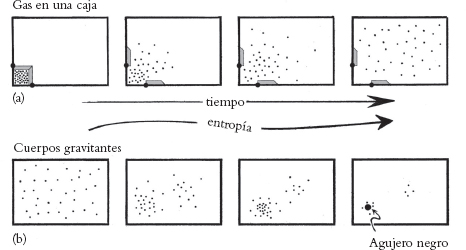
Fig. 2.8. (a) El gas está inicialmente confinado dentro de un pequeño compartimento en la esquina de una caja antes de ser liberado y difundirse uniformemente por toda la caja. (b) En una caja de tamaño galáctico, las estrellas están inicialmente distribuidas de manera uniforme pero con el tiempo de juntan en grumos: en este caso, una distribución uniforme no es la que tiene entropía más alta.

Podemos preguntar: ¿cuál es ahora el estado análogo al equilibrio térmico, donde la entropía ha alcanzado su máximo? Resulta que esta pregunta no puede ser adecuadamente abordada dentro de los confines de la teoría newtoniana. Si consideramos un sistema que consiste en partículas puntuales masivas que se atraen mutuamente según la ley de Newton de la inversa del cuadrado, entonces podemos concebir estados en los que algunas de las partículas se acercan cada vez más unas a otras, moviéndose cada vez más rápidas, de modo que no hay límite al grado de aglomeración y rapidez de movimiento, y el estado de «equilibrio térmico» propuesto simplemente no existe. La situación resulta ser mucho más satisfactoria en la teoría de Einstein, porque la «grumosidad» puede saturarse cuando la materia se conglomera en un agujero negro.

Llegaré a los agujeros negros con más detalle en §2.4, donde aprenderemos que la formación del agujero negro representa un enorme aumento en la entropía. De hecho, en la época actual de la evolución del universo, la mayor contribución a la entropía, con mucho, la aportan grandes agujeros negros, como el que hay en el centro de nuestra propia Vía Láctea, con una masa de unos 4.000.000 de veces la masa del Sol. Frente a la entropía total en tales objetos, la entropía del CMB, que previamente se había pensado que representaba la contribución dominante a la entropía del universo, resulta casi despreciable. Así, la entropía ha aumentado enormemente por condensación gravitatoria respecto a la que era cuando se creó el CMB.

Esto guarda relación con la segunda característica del CMB que se ha mencionado antes, a saber, su temperatura prácticamente uniforme sobre todo el cielo. ¿Hasta que punto es uniforme? Hay una ligera variación de temperatura que se entiende como un efecto Doppler, debida al hecho de que la Tierra no está exactamente en reposo con respecto a la distribución de masa del universo en conjunto. El movimiento de la Tierra se compone de varias contribuciones, tales como su movimiento en torno al Sol, el movimiento del Sol en la Vía Láctea, y el movimiento de la galaxia debido a influencias gravitatorias locales de otras distribuciones de masas relativamente próximas. Todo se combina para dar lo que se conoce como «movimiento propio» de la Tierra. Eso lleva a un aumento muy ligero en la temperatura aparente del CMB en la dirección del cielo hacia el que nos acercamos,^[2.20] y una muy ligera disminución en la dirección del cielo del que nos alejamos, con una pauta fácilmente calculable. Una vez hechas las oportunas correcciones, encontramos un CMB con una temperatura extraordinariamente uniforme sobre el cielo, con desviaciones de tan solo unas pocas partes en 10⁵.

Esto nos dice que, al menos sobre la superficie de la última dispersión, el universo era extraordinariamente uniforme, como la imagen de la derecha en la Fig. 2.8(a) y también como la imagen de la izquierda en la Fig. 2.8(b). Por consiguiente, es razonable suponer que mientras podamos ignorar la influencia de la gravedad, el contenido material del universo (en la última dispersión) tenía una entropía tan alta como podía alcanzar por sí solo. Después de todo, las influencias gravitatorias serían pequeñas debido a la uniformidad, pero era esta misma uniformidad en la distribución de materia la que ofrecía el potencial para los enormes aumentos de entropía posteriores cuando las influencias gravitatorias entraran en juego. Nuestra imagen de la entropía del Big Bang cambia así por completo una vez que consideramos la introducción de los grados de libertad gravitatorios. Es la hipótesis de que nuestro universo, en conjunto, está en muy estrecho acuerdo con la homogeneidad y la isotropía espacial —lo que se suele llamar «principio cosmológico»,^[2.21] básico para la cosmología FLRW y, en particular, para los modelos de Friedmann discutidos en §2.1— la que implica la enorme supresión de grados de libertad gravitatorios en el estado inicial. Esta primitiva uniformidad espacial representa la entropía inicial extraordinariamente baja del universo.

Una pregunta natural que hay que plantear es: ¿qué demonios tiene que ver esta uniformidad cosmológica con nuestra familiar Segunda Ley, que parece impregnar gran parte del comportamiento físico detallado en el mundo que conocemos? Hay multitud de ejemplos comunes de la Segunda Ley que no parecen guardar ninguna relación con el hecho de que los grados gravitatorios estuvieran suprimidos en el universo primitivo. Pero la conexión existe, y realmente no es difícil remitir estos ejemplos comunes de la Segunda Ley a la uniformidad del universo primitivo.

Consideremos, a modo de ejemplo, el huevo de §1.1 colocado al borde de una mesa, a punto de caer y aplastarse contra el suelo (véase la Fig. 1.1). El proceso de aumento de entropía del huevo que rueda por la mesa y se aplasta está enormemente favorecido, desde el punto de vista probabilista, siempre que estemos dispuestos a suponer que el huevo empezó en el estado de muy baja entropía en que estaba colocado, intacto, en el borde de la mesa. El enigma de la Segunda Ley no es el aumento de la entropía que sigue a este suceso; el enigma está en el propio suceso, es decir, la pregunta de cómo el huevo llegó a encontrarse antes de nada en ese estado de entropía extremadamente baja. La Segunda Ley nos dice que debe haber llegado a ese estado muy improbable a través de una secuencia de otros estados previos que habían sido aún más improbables, y se hacían todavía más improbables cuanto más atrás nos remontamos en el tiempo para examinar el sistema.

Básicamente hay dos cosas que explicar. Una es la cuestión de cómo llegó a estar el huevo sobre la mesa, y la otra es cómo se produjo la estructura de baja entropía de ese mismo huevo. De hecho, el material de un huevo (que suponemos un huevo de gallina) está soberbiamente organizado como un perfecto paquete alimenticio adecuado para un pretendido polluelo. Pero empecemos con lo que puede parecer que es la parte más fácil del problema, a saber, cómo llegó a encontrarse el huevo encima de la mesa. La respuesta probable sería que alguien lo puso allí, quizá de forma descuidada, pero la intervención humana fue la causa probable. Evidentemente hay mucha estructura altamente organizada en un ser humano, lo que sugiere una baja entropía, y la colocación del huevo sobre la mesa sólo habría tomado un poco del gran reservorio de baja entropía en el sistema relevante, consistente en una persona razonablemente bien alimentada y una atmósfera ambiente cargada de oxígeno. La situación con el propio huevo es similar, en cuanto que la estructura altamente organizada del huevo, soberbiamente engranada para apoyar la vida emergente de un embrión dentro de ella, es buena parte del gran esquema de cosas que mantiene la vida en este planeta. Todo el tejido de la vida en la Tierra requiere el mantenimiento de una organización profunda y sutil, lo que indudablemente implica que la entropía se mantenga en un bajo nivel. En detalle, hay una estructura enormemente intrincada e interconectada que ha evolucionado de la mano del principio biológico fundamental de la selección natural y de muchas cuestiones detalladas de química.

¿Qué tienen que ver, podría el lector preguntar, estas cuestiones de biología y de química con la uniformidad del universo primitivo? La complejidad biológica no permite que el sistema en conjunto viole leyes generales de la física, tal como la ley de conservación de la energía; además, no puede proporcionar un escape de las ligaduras impuestas por la Segunda Ley. La estructura de la vida en este planeta se degradaría rápidamente si no hubiera una poderosa fuente de baja entropía de la que depende casi toda la vida en la Tierra, a saber: el Sol.^[2.22] Se tiende a pensar que el Sol suministra a la Tierra una fuente externa de energía, pero esto no es del todo correcto, pues ¡la energía que recibe la Tierra cada día del Sol es esencialmente igual a la que devuelve la Tierra a la oscuridad del espacio!^[2.23] Si no fuera así, entonces la Tierra sencillamente se calentaría hasta alcanzar un equilibrio. De lo que depende la vida es del hecho de que el Sol está mucho más caliente que la oscuridad del espacio, y en consecuencia los fotones procedentes del Sol tienen una frecuencia considerablemente más alta (a saber, la de la luz amarilla) que la de los fotones infrarrojos que la Tierra devuelve al espacio. La fórmula de Planck E = hv (véase §2.3) nos dice entonces que, en promedio, la energía que lleva cada fotón individual procedente del Sol es considerablemente mayor que la energía que lleva cada fotón devuelto al espacio. Por consiguiente, el número de fotones que se llevan energía de la Tierra es mucho mayor que el número de fotones que traen esa misma energía procedentes del Sol. Véase la Fig. 2.9. Más fotones implican más grados de libertad, y en consecuencia un volumen mayor en el espacio de fases. Así pues, la fórmula S = klogV de Boltzmann (véase §1.3) nos dice que la energía que entra procedente del Sol transporta una entropía considerablemente más baja que la que vuelve al espacio.

Fig. 2.9. Los fotones que llegan a la superficie de la Tierra procedentes del Sol tienen una energía más alta (longitud de onda más corta) que los que la Tierra devuelve al espacio. Dado un balance de energía global (la Tierra no se calienta más con el paso del tiempo), debe haber más fotones que llegan que fotones que dejan la Tierra, es decir, la energía que llega tiene una entropía menor que la energía que sale.

Ahora bien, en la Tierra las plantas verdes han encontrado, en el proceso de fotosíntesis, una manera de convertir los fotones de frecuencia relativamente alta procedentes del Sol en fotones de frecuencia menor, utilizando esta ganancia en baja entropía para construir su sustancia extrayendo carbono del CO₂ en el aire y devolviendo O₂. Cuando los animales comen las plantas (o comen a otros animales que comen plantas), utilizan esta fuente de baja entropía, y el O₂, para reducir su propia entropía.^[2.24] Esto se aplica a los seres humanos, por supuesto, y también a los pollos, ¡y suministra la fuente de baja entropía necesaria para la construcción de nuestro huevo intacto y para colocarlo en la mesa!

Así que lo que el Sol hace por nosotros no es simplemente suministrarnos energía, sino proporcionarnos esta energía en una forma de baja entropía; de modo que si podemos reducir nuestra entropía (mediante las plantas verdes) es debido a que el Sol es un punto caliente en un cielo por lo demás oscuro. Si el cielo entero hubiera tenido la misma temperatura que el Sol, entonces su energía no habría sido utilizable para la vida en la Tierra. Esto se aplica también a la capacidad del Sol para elevar el agua de los océanos hasta las nubes, que una vez más depende crucialmente de esa diferencia de temperatura.

¿Por qué el Sol es un punto caliente en el cielo oscuro? Bueno, hay todo tipo de procesos complicados que ocurren en el interior del Sol, y las reacciones termonucleares que dan como resultado que el hidrógeno se convierta en helio desempeñan un papel importante en ello. Sin embargo, la cuestión clave es que el Sol está allí, y esto ha sido el resultado de la influencia gravitatoria que mantiene al Sol. Sin reacciones termonucleares el Sol seguiría brillando, pero se contraería y haría más caliente, y tendría una vida mucho más corta. En la Tierra sacamos partido evidentemente de dichas reacciones termonucleares, pero éstas ni siquiera podrían tener lugar si no fuera por la aglomeración gravitatoria que dio lugar al Sol en primer lugar. Por consiguiente, hay un potencial para formar estrellas (aunque por vía de procesos algo complicados en regiones adecuadas en el espacio), mediante incesantes procesos aglomeración gravitatoria con aumento de entropía, a partir de un material inicial que partió de un estado gravitatoriamente muy uniforme de baja entropía.

Todo esto es el resultado, en última instancia, del hecho de que se nos ha presentado un Big Bang de una naturaleza muy especial, donde la (relativamente) extrema pequeñez de la entropía se manifiesta en el hecho de que sus grados de libertad gravitatorios no estaban inicialmente activados. Ésta es una situación curiosamente sesgada, y para entenderla mejor trataré de profundizar un poco más, en las tres próximas secciones, en la bella descripción de la gravedad como espacio-tiempo curvo. Luego, en §2.6 y §3.1, volveré a la cuestión de la naturaleza de esta extraordinaria especialidad que realmente se muestra en nuestro Big Bang.