2.6. Para comprender en qué modo era especial el Big Bang

Volvamos a la cuestión básica que he estado tratando de abordar en esta parte, a saber, la cuestión de cómo nuestro universo fue resultado de un Big Bang tan extraordinariamente especial; y especial en cuanto que parece que surgió de un modo muy peculiar en que, con respecto a la gravedad, su entropía era enormemente baja en comparación con lo que podría haber sido, pero en cualquier otro aspecto la entropía estaba próxima a un máximo. Sin embargo, en muchas consideraciones cosmológicas modernas esta cuestión suele estar enturbiada por la idea muy divulgada de que en las etapas muy tempranas de la existencia del universo, éste sufrió una expansión exponencial, conocida como inflación cósmica, durante una fase que duró un período de tiempo minúsculo en algún momento comprendido entre 10⁻³⁶ y 10⁻³² segundos después del Big Bang, lo que aumentó las dimensiones lineales del universo en un factor enorme de un valor entre 10²⁰ y 10⁶⁰, o quizá incluso 10¹⁰⁰. Esta enorme expansión explicaría (entre otras cosas) la uniformidad del universo primitivo, pues se considera que prácticamente todas las irregularidades iniciales quedaron alisadas simplemente por la expansión. Sin embargo, estas consideraciones apenas parecen abordar la cuestión fundamental en la que me he interesado en la Parte 1, a saber, el origen de la extraordinariamente manifiesta especialidad del Big Bang, que debe haber estado presente inicialmente para que haya una segunda ley de la termodinámica. En mi opinión, esta idea que subyace en la inflación —que la uniformidad en el universo que ahora observamos debería ser el resultado de procesos físicos (inflacionarios) que actuaban durante su evolución temprana— está básicamente equivocada.

¿Por qué digo que está equivocada? Examinemos esta cuestión mediante algunas consideraciones generales. La dinámica que subyace en la inflación se considera gobernada de la misma forma general que lo están otros procesos físicos, para los que existen leyes dinámicas simétricas respecto al tiempo. Se considera que un campo físico particular conocido como «campo inflatón» es responsable de la inflación, aunque la naturaleza precisa de las ecuaciones que gobiernan el campo inflatón diferirá en general de una versión de la inflación a otra. Como parte del proceso inflacionario habría tenido lugar una especie de «transición de fase», que presenta ciertas analogías con la transición entre los estados sólido y líquido que ocurre en la congelación o la fusión, etc. Tales transiciones procederían de acuerdo con la Segunda Ley, y normalmente irían acompañadas de un aumento de la entropía. Por consiguiente, la inclusión de un campo inflatón en la dinámica del universo no afecta a los argumentos esenciales que se han presentado en la Parte 1. Seguimos necesitando entender la extraordinariamente baja entropía de salida del universo y, según los argumentos de §2.2, este bajo valor de la entropía se debe en esencia al hecho de que no estaban excitados los grados de libertad gravitatorios, al menos no hasta el extremo en que estaban implicados todos los demás grados de libertad.

Será ciertamente útil tratar de entender cómo sería un estado inicial de alta entropía cuando se toman en consideración los grados de libertad gravitatorios. Podemos hacernos una idea si imaginamos el contexto invertido en el tiempo de un universo en colapso, puesto que este colapso, si se toma de acuerdo con la Segunda Ley, debería llevarnos a un estado singular de entropía verdaderamente alta. Debería quedar claro que nuestra mera consideración de un universo en colapso no tiene nada que ver con que nuestro universo real vaya a recolapsar o no, como el modelo cerrado de Friedmann Λ = 0 de la Fig. 2.2. Ahora el colapso se está tomando simplemente como una situación hipotética, y está de acuerdo con las ecuaciones de Einstein. En una situación de colapso general, como los colapsos generales a un agujero negro que se han considerado en §2.4, cabe esperar que surjan irregularidades de todo tipo, pero cuando regiones locales de material se hacen suficientemente concentradas, es probable que resulten superficies atrapadas y cabe esperar que aparezcan singularidades espaciotemporales^[2.50] Cualesquiera irregularidades en la densidad que hubiera inicialmente se intensificarían enormemente, y cabría esperar que la singularidad final fuera la que resulta de un extraordinario amasijo de agujeros negros coalescentes. Aquí es donde muy bien podrían entrar en juego las consideraciones de Belinski, Jalatnikov y Lifshitz. Y si la conjetura BKL es correcta (véase §2.4), es de esperar una estructura de singularidad extremadamente complicada.

Volveré enseguida a esta cuestión de la estructura de la singularidad, pero por el momento consideremos la relevancia de la física inflacionaria. Centremos la atención en el estado del universo en, por ejemplo, el instante de desacoplamiento, cuando se produjo la radiación que vemos ahora como CMB (véase §2.2). En nuestro universo en expansión real hubo una uniformidad muy grande en la distribución de materia en ese instante. Evidentemente esto se considera un enigma, ¡pues de lo contrario no tendría sentido introducir la inflación para explicarlo! Puesto que se acepta que hay algo que explicar, debemos considerar que, en su lugar, podría haber habido enormes irregularidades en ese instante. Los inflacionistas tendrían que afirmar que la presencia de un campo inflación hace tales irregularidades altamente improbables. Pero ¿realmente es así?

En absoluto, pues podemos imaginar esta situación de una distribución de materia altamente aglomerada en el instante de desacoplamiento, pero con el tiempo invertido, de modo que esta imagen representa un universo en colapso muy irregular.^[2.51] Cuando nuestro universo imaginado colapsa hacia dentro, las irregularidades se amplificarán, y las desviaciones respecto a la simetría FLRW (véase §2.1) se harán cada vez más exageradas. Entonces, la situación estará tan lejos de la homogeneidad e isotropía FLRW que las capacidades inflacionarias del campo inflatón no encontrarán ningún papel, y la inflación (con el tiempo invertido) simplemente no tendrá lugar, puesto que depende crucialmente de tener un fondo FLRW (al menos en lo que concierne a cálculos que se han llevado a cabo realmente).

Por consiguiente, nos vemos llevados a la implicación clara de que nuestro modelo de colapso irregular colapsará en verdad a un estado que incluye un tremendo amasijo de agujeros negros coalescentes, lo que lleva a una singularidad muy complicada y de entropía enormemente alta, muy posiblemente de tipo BKL, que es muy diferente de la singularidad altamente uniforme y de baja entropía de forma FLRW muy aproximada que parece haber habido en nuestro Big Bang real. Esto habría sucedido independientemente de si está o no presente un campo inflatón en los procesos físicos admitidos. Así pues, si invertimos de nuevo en el tiempo nuestro imaginado universo aglomerado en colapso para obtener una imagen posible de un universo en expansión, encontramos que empieza con una singularidad de alta entropía que, así parece, podría haber sido un estado inicial para nuestro universo real que, en verdad, sería un estado inicial mucho más probable (es decir, de mucha mayor entropía) que el Big Bang que ocurrió realmente. Los agujeros negros que se fusionan en las etapas finales de nuestro colapso ideado nos proporcionarían, cuando se invierte el tiempo en un universo en expansión, la imagen de una singularidad inicial que consiste en agujeros blancos que se bifurcan múltiplemente.^[2.52] Un agujero blanco es el inverso en el tiempo de un agujero negro, y en la Fig. 2.45 he indicado el tipo de situación que esto nos presenta. Es la total ausencia de tales singularidades de agujero blanco lo que discrimina nuestro Big Bang como algo extraordinariamente especial.

Fig. 2.45. Un hipotético «agujero blanco», que es el inverso en el tiempo de un agujero negro, tal como se muestra en la Fig. 2.24. Desobedece violentamente la Segunda Ley. La luz no puede cruzar el horizonte, de modo que la luz de la antorcha en la parte inferior izquierda entra solamente cuando el agujero explota.

En términos de volumen del espacio de fases, las singularidades iniciales de esta naturaleza (con agujeros blancos múltiplemente bifurcantes) ocuparían una región inmensamente mayor que las similares a la singularidad que dio lugar a nuestro Big Bang real. Ciertamente, la mera presencia potencial de un campo inflatón no puede proporcionar la capacidad de alisar las irregularidades de tal conglomerado de singularidades de agujero blanco. Puede decirse esto con fiabilidad al margen de cualesquiera consideraciones detalladas de la naturaleza del campo inflatón. Se trata simplemente de tener ecuaciones que puedan evolucionar por igual en cualquier dirección en el tiempo, hasta que se alcanza un estado singular.

Pero ciertamente podemos decir más sobre la enormidad real del volumen del espacio de fases si tenemos en cuenta los valores de la entropía, y por consiguiente los volúmenes de espacio de fases, que se asignan realmente a los agujeros negros, según la bien aceptada fórmula de Bekenstein-Hawking para el valor de la entropía de un agujero negro. Para un agujero negro no rotatorio de masa M, esta entropía es

mientras que si el agujero negro está rotando, su entropía está entre este valor y la mitad del mismo, dependiendo de la cantidad de rotación. La fracción que precede a «M²» es simplemente una constante, donde k, G y h son las constantes de Boltzmann, Newton y Planck, respectivamente, y c es la velocidad de la luz. De hecho, podemos reescribir esta fórmula para la entropía en una forma más general

donde A es el área de la superficie del horizonte, y esta fórmula es aplicable ya esté el agujero rotando o no. En las unidades de Planck introducidas al final de §3.2, tenemos

S_BH = A/4

Aunque, en mi opinión, no hay todavía una explicación completamente satisfactoria de esta entropía en términos del recuento de estados de agujero negro internos,^[2.53] este valor de la entropía es de todas formas un ingrediente esencial para el mantenimiento de una Segunda Ley consistente en un mundo físico-cuántico externo al agujero negro. Como ya se ha mencionado en §2.2, la mayor contribución a la entropía del universo actual procede de grandes agujeros negros en los centros galácticos. Si una masa total similar a la que se encuentra dentro de nuestro universo observable actual (que se encuentra dentro de nuestro horizonte de partículas actual; véase §2.5) fuera a formar un agujero negro, éste alcanzaría una entropía del orden de 10¹²⁴, y podemos considerar que esto proporciona una cota inferior aproximada para la entropía que podría alcanzar nuestro modelo de universo en colapso que incluye la misma cantidad de materia. El volumen del espacio de fases correspondiente a esto sería entonces algo como^[2.54]

10¹⁰¹²⁴

(debido al logaritmo en la fórmula de la entropía de Boltzmann, dada en §1.3), mientras que la región del espacio de fases correspondiente al estado del universo observado real en el instante de desacoplamiento, para la misma cantidad de materia, a saber, la del CMB observado, tenía un volumen no mayor que

10¹⁰⁸⁹

La probabilidad de que nos encontremos en un universo de un carácter tan especial, si se hubiera producido por azar,^[2.55] tiene el valor absurdamente minúsculo de 1/10¹⁰¹²⁴ con independencia de la inflación. ¡Éste es el tipo de cifra que necesita una explicación teórica de un tipo completamente diferente!

Hay, sin embargo, otra cuestión que puede tener importancia aquí. Es la cuestión de si una singularidad inicial de una estructura tan complicada de tipo agujero blanco podría razonablemente calificarse como un «suceso instantáneo». Se trata básicamente de si tal singularidad, cuando se ve como un tipo de «frontera conforme» pasada para el espacio-tiempo, puede considerarse apropiadamente como «de tipo espacio». Tal singularidad inicial de tipo espacio podría representar el cero de una coordenada temporal cósmica y considerarse como el «momento» de dicho big bang altamente irregular.

Fig. 2.46. Diagrama conforme estricto del agujero blanco en la Fig. 2.45.

De hecho, el inverso en el tiempo de un colapso de Oppenheimer-Snyder tiene una singularidad inicial de tipo espacio, como es evidente de su diagrama conforme estricto en la Fig. 2.46, que es el inverso en el tiempo de la Fig. 2.38(a). Además, una propiedad de las singularidades BKL generales es que parecen tener este carácter de tipo espacio. Con más generalidad aún, una naturaleza de tipo espacio es de esperar para singularidades genéricas (admitiendo que sean posiblemente nulas en algunos lugares) sobre la base de la censura cósmica fuerte,^[2.56] una conjetura aún no probada para soluciones de las ecuaciones de Einstein (ya mencionada en §2.4) que nos dice que no se producen «singularidades desnudas» en un colapso gravitatorio genérico, y las singularidades que resultan están siempre ocultas a la observación directa, como por un horizonte de sucesos de agujero negro. La censura cósmica fuerte nos dice que dichas singularidades deberían ser de tipo espacio, al menos en general. De acuerdo con esta expectativa, me parece perfectamente razonable calificar tal singularidad inicial de agujero blanco como un suceso instantáneo.

Surge ahora una pregunta importante: ¿qué criterio geométrico distingue el tipo de singularidad «suave», que parece ser lo que caracteriza a la singularidad de muy baja entropía de nuestro Big Bang, del tipo más general de singularidad de alta entropía que aparece en los recién considerados colapsos de agujeros blancos invertidos en el tiempo? Necesitamos un modo preciso de decir que «los grados de libertad gravitatorios no estaban activados». Pero para esto necesitamos identificar la magnitud matemática que realmente mide los «grados de libertad gravitatorios».

Una buena analogía para el campo gravitatorio es el campo electromagnético, que se le parece en muchos aspectos, aunque hay, no obstante, algunas diferencias importantes. En la física relativista el campo electromagnético se describe mediante una magnitud tensorial F conocida como campo tensorial de Maxwell, por el gran científico escocés James Clerk Maxwell, quien fue el primero en encontrar, en 1861, las ecuaciones que satisfacen el campo electromagnético y demostró que éstas explicaban la propagación de la luz. Recordemos que en §2.3 encontramos otra magnitud tensorial, a saber, el tensor métrico g. Los tensores son esenciales para la teoría de la relatividad general, pues proporcionan descripciones matemáticas de entidades geométricas o físicas en formas que no se ven afectadas (o «arrastradas») por las deformaciones de «lámina elástica» (difeomorfismos) que se han considerado en §2.3. El tensor F está determinado por 6 números independientes por cada punto (3 para las componentes del campo eléctrico en dicho punto y otros 3 para el campo magnético). El tensor métrico g tiene 10 componentes independientes por punto. En notación tensorial estándar es habitual denotar el conjunto de componentes de la métrica por g_ab, o algo similar, con dos subíndices (y tiene una simetría g_ab = g_ba). En el caso del tensor de Maxwell F, el conjunto de componentes se denotará por F_ab (con la antisimetría F_ab = −F_ba). Cada uno de estos tensores tiene una valencia , que se refiere al hecho de que sólo hay dos subíndices. Pero también pueden darse tensores con superíndices, y un -tensor se describe por un conjunto de componentes denotado por una entidad con p superíndices y q subíndices. Hay un procedimiento algebraico conocido como contracción (o transvección) que nos permite conectar un subíndice con un superíndice (un poco al modo de un enlace químico), lo que elimina estos dos índices de la expresión final —pero no es mi objetivo aquí entrar en las operaciones algebraicas del cálculo tensorial—.

Los grados de libertad en el campo electromagnético son medidos por el tensor de Maxwell F, pero en la teoría de Maxwell hay también una fuente para el campo electromagnético, conocida como vector carga-corriente J. Este puede considerarse como un -tensor, cuyas 4 componentes por punto describen la 1 componente de la densidad de carga eléctrica junto con las 3 componentes de la corriente eléctrica. En una situación estacionaria, la densidad de carga actúa como la fuente de campo eléctrico y la densidad de corriente como la fuente de campo magnético, pero las cosas se complican cuando la situación no es estacionaria.

Ahora preguntamos por las magnitudes que desempeñan papeles análogos a los de F y J en el caso del campo gravitatorio, tal como es descrito por la teoría de la relatividad general de Einstein. En esta teoría hay una curvatura para el espacio-tiempo (que puede calcularse una vez que se sabe cómo varía la métrica g a lo largo del espacio-tiempo), descrita por un -tensor R, llamado tensor de Riemann(-Christoffel), con simetrías algo complicadas que dan como resultado que R tiene 20 componentes independientes por punto. Estas componentes pueden separarse en dos partes, que constituyen un -tensor C, con 10 componentes independientes, llamado tensor conforme de Weyl, y un -tensor simétrico E, también con 10 componentes independientes, llamado tensor de Einstein (que es equivalente a un -tensor ligeramente diferente conocido como tensor de Ricci^[2.57]). Según las ecuaciones de campo de Einstein, es E el que proporciona la fuente para el campo gravitatorio. Esto se expresa normalmente^[2.58] en la forma

o, en unidades de Planck de §3.2, simplemente

E = 8πT + Λg,

donde Λ es la constante cosmológica, y donde el -tensor de energía T representa la densidad de masa-energía y otras cantidades relacionadas con ella por vía de requisitos de relatividad; en otras palabras, E (o equivalentemente, el tensor energía T) es el análogo gravitatorio a J. El tensor de Weyl C es entonces el análogo gravitatorio al tensor F de Maxwell.

Podemos preguntar qué efectos directamente observables podrían tener C y E, algo similar a cómo los campos magnéticos se manifiestan por las figuras de limaduras de hierro o por la orientación de una brújula, y cómo los campos eléctricos se revelan por su efecto sobre bolas de médula, etc. De hecho, en un sentido casi literal, podemos ver realmente los efectos de E y más particularmente C, puesto que estos tensores tienen un efecto directo y característico sobre los rayos de luz; y a este respecto E y T son completamente equivalentes, puesto que Ag no tiene ningún efecto sobre los rayos de luz. Puede decirse que la primera prueba clara en apoyo de la relatividad general fue precisamente dicha observación directa, que fue el resultado de la expedición de (sir) Arthur Eddington a la isla del Príncipe para ver, durante el eclipse solar de 1919, el aparente desplazamiento de las localizaciones de las estrellas debido al campo gravitatorio del Sol.

Básicamente, E actúa como una lente de aumento, mientras que C actúa como una lente puramente astigmática. Estos efectos se describen bien si imaginamos cómo son afectados los rayos de luz cuando pasan cerca o a través de un cuerpo masivo, tal como el Sol. Por supuesto, la luz ordinaria no se propagará realmente a través del Sol (o de la Luna interpuesta durante el eclipse), de modo que no observamos directamente estos rayos concretos. Pero podemos imaginar que si realmente pudiéramos ver el campo estelar a través del Sol, entonces dicho campo estaría ligeramente ampliado, debido a la presencia de E, allí donde reside el material gravitatorio del cuerpo real del Sol. El puro efecto de E sería simplemente ampliarla «vista» de lo que hay detrás, sin distorsionarlo.^[2.59] Sin embargo, cuando se trata de la imagen del campo estelar lejano fuera del disco aparente del Sol (y esto es lo que se observa realmente) encontramos una reducción gradual del desplazamiento hacia fuera cuanto más lejos miramos, y esto lleva a una distorsión astigmática del campo estelar lejano. Esos efectos se ilustran en la Fig. 2.47. La distorsión del campo fuera del borde del Sol hace que una pequeña figura circular en el campo estelar lejano aparezca elíptica, y esta elipticidad es una medida de la cantidad de curvatura de Weyl C interceptada por la línea visual.

De hecho, este efecto de lente gravitatoria, originalmente predicho por Einstein, se ha convertido en una herramienta en extremo importante en la astronomía y la cosmología modernas, puesto que proporciona un medio de medir distribuciones de masa que de otro modo podría ser incluso completamente invisible. En la mayoría de estos casos el campo de fondo lejano consiste en un gran número de galaxias muy lejanas. El objetivo es determinar si se ha introducido elipticidad significativa en la apariencia de este campo de fondo, y utilizar esto para estimar la distribución de la masa real interpuesta cuyo campo gravitatorio ha provocado la pauta de elipticidades. Sin embargo, una pega es que las propias galaxias suelen ser elípticas, de modo que habitualmente no se puede decir si la imagen de una galaxia individual ha sido o no distorsionada. No obstante, con grandes números de galaxias en el campo de fondo se puede recurrir a la estadística, y con frecuencia pueden obtenerse de este modo muy buenas estimaciones de las distribuciones de masa. En ocasiones es posible incluso juzgar estas cosas a simple vista, y algunos ejemplos impresionantes se dan en la Fig. 2.48, donde las pautas de elipticidad dejan particularmente clara la presencia de fuentes de lentes gravitatorias. Una aplicación importante de esta técnica está en la cartografía de distribuciones de materia oscura (véase §2.1), puesto que éstas son de otro modo invisibles.^[2.60]

Fig. 2.47. La presencia de la curvatura de Weyl alrededor de un cuerpo gravitante (aquí el Sol) puede verse en el efecto distorsionador (no conforme) que tiene en el campo de fondo.

El hecho de que C introduce elipticidad en las imágenes a lo largo de los rayos de luz es indicativo de su papel como la magnitud que describe la curvatura conforme. Al final de §2.3 se ha comentado que la estructura conforme del espacio-tiempo es de hecho su estructura de conos nulos. La curvatura conforme del espacio tiempo, a saber C, mide por ello la desviación de esta estructura de conos nulos respecto de la del espacio de Minkowski . Vemos que la naturaleza de esta desviación consiste en que introduce elipticidad en haces de rayos luminosos.

Fig. 2.48. Efecto de lente gravitatoria: (a) cúmulo galáctico Abell, 1689; (b) cúmulo galáctico SDSS J1004 + 4112.

Llegamos ahora a la condición que requerimos para caracterizar la estructura muy especial del Big Bang. Básicamente requerimos una afirmación de que los grados de libertad gravitatorios no estaban excitados en el Big Bang, lo que significa decir algo como «la curvatura de Weyl C se anulaba allí». Durante muchos años he estado proponiendo que alguna condición de este tipo «C = 0» es válida en singularidades iniciales, frente a lo que evidentemente sucede en las singularidades «finales» que se dan en agujeros negros para las que C probablemente se hace infinita, como lo hace la singularidad en el colapso Oppenheimer-Snyder, y que quizá divergen de forma incontrolada, como en las singularidades BKL.^[2.61] En términos generales, esta condición de la anulación de C en singularidades iniciales —a la que he llamado hipótesis de curvatura de Weyl (o HCW)— parece apropiada, pero resulta algo incómodo que haya en efecto muchas versiones diferentes de dicho enunciado. El problema es, básicamente, que C es una magnitud tensorial y es difícil hacer afirmaciones matemáticas inequívocas acerca de cómo se comportan estas magnitudes en las singularidades espaciotemporales, donde la propia noción de un tensor, en el sentido ordinario, pierde su significado.

Por ello, es una suerte que mi colega de Oxford Paul Tod haya hecho un estudio detallado de una manera muy diferente, y matemáticamente mucho más satisfactoria, de formular una «HCW». Consiste en decir, más o menos, que hay una 3-superficie Big Bang ⁻ que actúa como una frontera pasada suave para el espacio-tiempo , cuando se considera como una variedad conforme, como sucede en los modelos FLRW exactamente simétricos tal como se muestra en los diagramas conformes estrictos de la Fig. 2.34 y la Fig. 2.35, pero donde ahora no se supone la simetría FLRW de estos modelos particulares. Véase la Fig. 2.49. Al menos la propuesta de Tod obliga a C a ser finita en el Big Bang (puesto que se supone que la estructura conforme en ⁻ es suave), en lugar de divergir desbocadamente, y este enunciado muy bien podría ser suficiente para lo que se requiere.

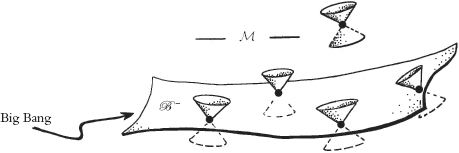
Fig. 2.49. Diagrama conforme esquemático de la propuesta de Paul Tod para una forma de «hipótesis de curvatura de Weyl»; afirma que el Big Bang proporciona una frontera suave para el espacio-tiempo .

Para hacer esta condición matemáticamente más clara es conveniente enunciarla en esta otra forma: el espacio-tiempo puede ser continuado suavemente, como una variedad conforme, hasta un poco antes de la hipersuperficie ⁻. ¿Hasta antes del Big Bang? Por supuesto que no: se supone que el Big Bang representa el comienzo de todas las cosas, de modo que no puede haber «antes». No hay que tener miedo, esto es sólo un truco matemático. ¡Se supone que la extensión no tiene significado físico!

¿O podría tenerlo…?