3.4. Cuadrando la Segunda Ley

Volvamos por ello a la cuestión que puso en marcha toda esta empresa, a saber, el origen de la Segunda Ley. El primer punto que se ha de señalar es que hay que afrontar un enigma. Es un enigma que parece asaltarnos independientemente de la CCC. La cuestión tiene que ver con el hecho evidente de que la entropía de nuestro universo —o del eón actual, si estamos considerando la CCC— parece estar aumentando enormemente, pese al hecho de que el universo muy primitivo y el futuro muy remoto parecen ser incómodamente similares uno a otro. Por supuesto, no son realmente similares en el sentido de ser casi idénticos, pero son alarmantemente «similares» de acuerdo con el uso que se hace normalmente de esta palabra en geometría euclidiana, a saber, que la diferencia entre los dos parece ser básicamente tan solo un enorme cambio de escala. Además, cualquier cambio de escala global es esencialmente irrelevante para las medidas de entropía —donde esta magnitud está definida por la maravillosa fórmula de Boltzmann (que se ha dado en §1.3)— debido al hecho importante, señalado al final de §3.1, de que los volúmenes del espacio de fases no son alterados por cambios de escala conformes.^[3.40] Pese a todo, la entropía sí parece aumentar, enormemente, en nuestro universo, debido a los efectos de aglomeración gravitatoria. Nuestro enigma consiste en entender cómo pueden cuadrarse estos hechos aparentes. Algunos físicos han argumentado que la definitiva máxima entropía alcanzada por nuestro universo no aparecerá de la aglomeración en agujeros negros, sino de la entropía de Bekenstein-Hawking del horizonte de sucesos cosmológico. Esta posibilidad será abordada en §3.5, donde argumentaré que ello no invalida la discusión de esta sección.

Examinemos con más cuidado el estado probable del universo primitivo, donde se ha impuesto alguna condición apropiada para eliminar los grados de libertad gravitatorios en el Big Bang, de modo que esta entropía gravitatoria es baja en lo que encontramos en el universo primitivo. ¿Necesitamos tener en cuenta la inflación cósmica? El lector se habrá dado cuenta de que soy escéptico sobre la realidad de este presunto proceso (§2.6), pero no importa; en esta discusión apenas supone alguna diferencia. Podemos o bien ignorar la posibilidad de inflación, o quizá adoptar el punto de vista (véase §3.6) de que la CCC proporciona meramente una interpretación diferente de la inflación, en donde la fase inflacionaria es la fase en expansión exponencial del eón previo, o podemos considerar la situación inmediatamente después del «momento» cósmico —alrededor de 10⁻³² s—, cuando se considera que la inflación ha cesado.

Como he argumentado al comienzo de §3.1, es razonable suponer que este estado de universo primitivo (digamos alrededor de 10⁻³² s) estaría dominado por física conformemente invariante y habitado por ingredientes sin masa efectiva. Ya sea o no correcta en todos sus detalles la propuesta de Tod, de §2.6, parece que no nos equivocamos demasiado si tomamos el estado del universo primitivo, en el que los grados de libertad gravitatorios están fuertemente suprimidos, como uno en el que un estiramiento conforme nos proporcionaría un estado suave no singular que sigue estando habitado en esencia por entidades sin masa, quizá básicamente fotones. Asimismo tendríamos que tener en cuenta los grados de libertad adicionales en la materia oscura, que también se considera sin masa efectiva en esos instantes iniciales.

En el otro lado de la escala de tiempos, tenemos finalmente un universo de tipo De Sitter (§2.5) en expansión exponencial, una vez más habitado básicamente por ingredientes sin masa (fotones). Podría haber muy bien otro material perdido consistente, digamos, en partículas masivas estables, pero la entropía estaría casi enteramente en los fotones. Parece que seguiríamos sin equivocarnos demasiado (apelando a los resultados de Friedrich citados en §3.1) si suponemos que podemos comprimir conformemente el futuro remoto para obtener un estado de universo suave nada diferente del que obtuvimos estirando conformemente la situación próxima al Big Bang (digamos en 10⁻³² s). Si acaso, podría haber más grados de libertad activados en el Big Bang estirado, porque, además de los grados de libertad quizá activados en la materia oscura, la propuesta de Tod aún permite la presencia de grados de libertad gravitatorios en un tensor de Weyl C no nulo (pero finito), y no el requisito C = 0 demandado por la CCC (véanse §2.6 y §3.2). Pero si tales grados de libertad están realmente presentes, esto solo hará nuestro enigma aún más serio, pues el problema que hay que afrontar es que la entropía del universo muy primitivo se ve apenas menor (si no realmente mayor) que la que se va a encontrar en el futuro muy remoto, pese al hecho de que seguramente debe haber incrementos absolutamente enormes en la entropía que tienen lugar entre 10⁻³² s y el futuro muy remoto.

Para abordar adecuadamente este enigma tenemos que entender la naturaleza y magnitud de las contribuciones importantes a lo que esperamos que sea un enorme incremento de entropía. En el momento presente parece que la mayor contribución a la entropía del universo proviene de enormes agujeros negros en los centros de muchas (¿o todas?) galaxias. Es difícil encontrar una estimación precisa de los tamaños de los agujeros negros en las galaxias en general. ¡Por su misma naturaleza, los agujeros negros son difíciles de ver! Pero nuestra propia galaxia puede ser bastante típica, y parece que contiene un agujero negro de unas 4 × 10⁶ Mʘ (véase §2.4), que por la fórmula de entropía de Bekenstein-Hawking nos proporciona una entropía por barión para nuestra galaxia de unos 10²¹ (donde «barión» significa aquí, en efecto, un protón o un neutrón, y donde, por facilidad de descripción, estoy considerando que el número bariónico se conserva, pues todavía no se ha observado ninguna violación de este principio de conservación). Así que tomaremos esta cifra como una estimación plausible de la presente entropía por barión en el universo en general.^[3.41] Si tenemos en cuenta que la siguiente contribución a la entropía parece ser la del CMB, donde la entropía por barión no es más que de unos 10⁹, vemos cuánto parece haber aumentado ya la entropía desde el instante del desacoplamiento —y ya no digamos desde 10⁻³² s—, y es básicamente la entropía de los agujeros negros la responsable de este enorme incremento de entropía. Para hacer esto más espectacular, permítaseme escribirlo en una notación más habitual. La entropía por barión en el CMB es alrededor de 1.000.000.000, mientras que (según la estimación anterior), la entropía actual por barión es aproximadamente

1.000.000.000.000.000.000.000,

y está principalmente en los agujeros negros. Además, cabe esperar que estos agujeros negros, y en consecuencia la entropía del universo, crezca de manera muy considerable en el futuro, de modo que incluso este número quedará superado abrumadoramente en el futuro lejano. Así pues, nuestro enigma toma la forma de la pregunta: ¿cómo puede cuadrarse esto con lo que se ha dicho en las partes anteriores de esta sección? ¿Qué habrá sucedido en última instancia con toda esta entropía de agujeros negros?

Tenemos que tratar de entender cómo la entropía parecerá haberse contraído finalmente en un factor tan enorme. Para ver dónde ha ido toda esta entropía, recordemos lo que se supone que es el destino, en el futuro muy remoto, de todos esos agujeros negros responsables de ese enorme incremento de entropía. De acuerdo con lo que se ha dicho en §2.5, al cabo de unos 10¹⁰⁰ años los agujeros habrán desaparecido, habiéndose evaporado por el proceso de radiación de Hawking por el que se presume que cada uno de ellos desaparece finalmente con un «pop».

Debemos tener en cuenta que el crecimiento de la entropía debido al engullimiento de material por un agujero negro, y también la reducción final del tamaño (y masa) del agujero debido a su evaporación de Hawking, serían totalmente compatibles con la Segunda Ley; no solo eso, sino que también estos fenómenos son consecuencias directas de la Segunda Ley. Para apreciarlo, en líneas generales, no necesitamos entender las sutilezas del argumento inicial de Hawking en 1974 para la temperatura y la entropía de un agujero negro (que se considera formado en el pasado lejano a partir de un colapso gravitatorio). Si no estamos interesados en el coeficiente exacto 8kGπ²/ch que aparece en la fórmula de la entropía de Bekenstein-Hawking de §2.6, y nos contentamos con una aproximación al mismo, podríamos encontrar una justificación para la forma general de la entropía de un agujero negro simplemente a partir de la demostración original de Bekenstein en 1972^[3.42]; ésta utilizaba un argumento exclusivamente físico basado en la Segunda Ley y en los principios de la mecánica cuántica y la relatividad general aplicados a experimentos mentales concernientes a la caída de objetos al interior de agujeros negros. La temperatura de superficie de agujero negro de Hawking T_BH, que para un agujero sin rotación de masa M es

(estando dada la constante K por K = 1/(4π)), se sigue entonces de principios termodinámicos estándar^[3.43] una vez que se acepta la fórmula de la entropía. Ésta es la temperatura vista desde el infinito, y el ritmo al que radiará un agujero negro se determina entonces suponiendo que esta temperatura se difunde uniformemente sobre una esfera cuyo radio es el radio de Schwarzschild (véase §2.4) del agujero negro.

Hago hincapié en estos puntos solo para resaltar que la entropía y temperatura de agujero negro, y el proceso de evaporación de Hawking de estas extrañas entidades, aunque de un carácter poco familiar, son sin embargo una buena parte de la física de nuestro universo, que encaja con principios fundamentales a los que nos hemos habituado, y muy especialmente con la Segunda Ley. La enorme entropía que poseen los agujeros negros es algo que cabe esperar de su carácter irreversible y el hecho notable de que la estructura de un agujero negro estacionario solo necesita unos pocos parámetros para caracterizar su estado.^[3.44] Puesto que debe haber un enorme volumen de espacio de fases correspondiente a cualquier conjunto concreto de valores de tales parámetros, la fórmula de Boltzmann (§1.3) sugiere una entropía muy grande. De la consistencia de la física en conjunto tenemos muchas razones para esperar que nuestra actual imagen general del papel y el comportamiento de los agujeros negros sea cierta, salvo que el «pop» al final de la existencia del agujero es algo hipotético. Sin embargo, es difícil ver qué otra cosa podría sucederle en esta etapa.

Pero ¿realmente necesitamos creer en el pop? Mientras el espaciotiempo descrito por el agujero negro siga siendo una geometría clásica (es decir, no cuántica), la radiación debería continuar extrayendo masa/energía del agujero a un ritmo tal que le haría desaparecer en un tiempo finito —de ~2 × 10⁶⁷(M/Mʘ)³ años para un agujero de masa M si nada más cae en el agujero—.^[3.45] Pero ¿cuánto tiempo podemos esperar que las nociones de la geometría espaciotemporal clásica ofrezcan una imagen fiable? La expectativa general (simplemente por consideraciones dimensionales) es que solo cuando el agujero se acerca a la absurdamente minúscula dimensión de Planck l_P de ~10⁻³⁵ m (aproximadamente 10⁻²⁰ del radio clásico de un protón) esperamos tener que incluir alguna forma de gravedad cuántica; pero sea lo que sea lo que suceda en esa etapa muy tardía, la única masa que queda sería presumiblemente algo cercano a la masa de Planck m_P, con un contenido de energía de solo una energía de Planck E_P, y es difícil ver que pudiera durar entonces un tiempo mucho mayor que un tiempo de Planck t_P (véase el final de §3.2). Algunos físicos han contemplado la posibilidad de que el punto final podría ser un remanente estable de masa ~m_P, pero esto causa algunas dificultades con la teoría cuántica de campos.^[3.46] Además, cualquiera que pudiera ser el destino final de un agujero negro, su estado de existencia final parece ser independiente del tamaño original del agujero negro, y solo tiene que ver con una extraordinariamente minúscula fracción de la masa-energía del agujero negro. No parece haber un acuerdo completo entre los físicos acerca del estado final de este minúsculo remanente de un agujero negro,^[3.47] pero la CCC requeriría que nada con masa en reposo persistiera por una eternidad, de modo que la imagen del «pop» (junto con la desintegración final de la masa en reposo de cualquier partícula masiva producida en el pop) es muy aceptable desde el punto de vista de la CCC, y es también compatible con la Segunda Ley.

Pero, pese a esta compatibilidad, hay algo característicamente singular en un agujero negro, en cuanto que la evolución futura del espaciotiempo, aparentemente única entre los fenómenos físicos de evolución futura, da como resultado una inevitable singularidad espaciotemporal interna. Aunque esta singularidad es una consecuencia de la relatividad general clásica (§2.4 y §2.6), es difícil creer que esta descripción clásica tuviera que ser seriamente modificada por consideraciones de gravedad cuántica antes de llegar a enormes curvaturas espaciotemporales donde los radios de curvatura del espacio-tiempo empiezan a reducirse a la escala extremadamente minúscula de la longitud de Planck l_P (véase el final de §3.2). Particularmente en el caso de un enorme agujero negro en un centro galáctico, el lugar donde empiecen a mostrarse tales radios de curvatura minúsculos será una región absolutamente minúscula que abarca a la singularidad en la imagen espaciotemporal clásica. La localización conocida como una «singularidad» en la descripción espaciotemporal clásica debería considerarse realmente como la localización «donde la gravedad domina». Pero en la práctica esto apenas supone diferencia, puesto que no hay una estructura matemática generalmente aceptada para reemplazar a la imagen de Einstein de espacio-tiempo continuo, y no preguntamos qué más sucede sino que meramente añadimos una frontera singular de curvatura desmesuradamente divergente, posiblemente de acuerdo con un comportamiento caótico de tipo BKL (§2.4 y §2.6).

Para hacernos una idea mejor del papel de esta singularidad en la imagen clásica, examinemos el diagrama conforme estricto de la Fig. 3.13, cuyas dos partes son básicamente redibujos de la Fig. 2.38(a) y la Fig. 2.41, respectivamente. Estas imágenes, cuando se interpretan como diagramas conformes estrictos, incorporan simetría esférica exacta, que es poco probable que siga existiendo cuando quiera que haya irregularidades presentes en el colapso. Sin embargo, si nos permitimos suponer censura cósmica fuerte (véase el final de §2.5 y §2.6) hasta justo antes del pop,^[3.48] entonces la singularidad debería ser esencialmente de tipo espacio, y las imágenes de la Fig. 3.13 siguen siendo cualitativamente adecuadas como diagramas conformes esquemáticos, pese a la extrema irregularidad en la geometría espaciotemporal cerca de la singularidad clásica.

Fig. 3.13. Diagramas conformes dibujados de forma irregular (para sugerir una falta de simetría) para indicar (a) colapso gravitatorio a un agujero negro; (b) colapso seguido de evaporación de Hawking. La singularidad sigue siendo de tipo espacio de acuerdo con la censura cósmica fuerte.

Las regiones donde cabría esperar que los efectos de gravedad cuántica invaliden la imagen espaciotemporal clásica estarían muy próximas a la singularidad, donde las curvaturas espaciotemporales empiezan a alcanzar los valores extremos donde ya no se puede confiar en la física espaciotemporal clásica. En esta etapa no parece que haya esperanzas de adoptar una posición como la implicada en las «3-superficies de tránsito» de la CCC, en la que el espacio-tiempo podría extenderse suavemente a través de la singularidad para llegar a un tipo de continuación que pase «al otro lado». De hecho, la propuesta de Tod pretende distinguir la singularidad muy domesticada encontrada en el Big Bang del tipo de actividad —quizá de naturaleza BKL caótica— que cabría esperar en una singularidad de agujero negro. Pese a la estimulante propuesta de Smolin descrita en §3.3 (Fig. 3.12), yo no tengo muchas esperanzas en que la gravedad cuántica venga en nuestra ayuda y nos permita obtener un «rebote», en el que el espacio-tiempo emergente refleje lo que entró, en cualquier sentido directo, de acuerdo con algún tipo de procesos físicos fundamentales básicamente simétricos respecto al tiempo. Si se pudiera, entonces lo que emerge sería algo de la naturaleza del agujero blanco de la Fig. 2.46 o el amasijo de agujeros blancos bifurcantes que hemos contemplado en §2.6 (contrástese con la Fig. 3.2).Tal comportamiento sería ciertamente muy diferente del tipo de situación que encontramos en el universo que nos es familiar, y no poseería nada parecido a la Segunda Ley de nuestras experiencias.

Como quiera que sea, lo que parece estar sucediendo —al menos según cualquier tipo de evolución física que seamos capaces de contemplar— es que la física llega a un final en dicha región. O, si no lo hace, entonces continúa en algún tipo de estructura de universo de un carácter completamente ajeno al que conocemos. En cualquier caso, el material que entra en la región singular se pierde para el universo que conocemos, y parece que cualquier información que porta el material también se pierde. Pero ¿se pierde? ¿O de alguna manera puede salirse de su camino, en el diagrama de la Fig. 3.13(b), donde distorsiones gravitocuánticas de las ideas normales de la geometría espaciotemporal permiten de algún modo una propagación aparentemente de tipo espacio que sería ilegal de acuerdo con las reglas de causalidad normales de §2.3? Incluso si es así, es difícil ver que algo de esta información pudiera reaparecer, por tales medios, mucho antes del momento del pop; de manera que la inmensa cantidad de información contenida en el material que iba a formar un gran agujero negro, digamos de muchos millones de masas solares, podría reaparecer de algún modo casi en ese mismo momento, y de esa minúscula región, que constituye el pop. Personalmente, encuentro esto muy difícil de creer. Para mí es mucho más plausible que la información contenida en todos los procesos cuya evolución futura se dirige hacia dicha singularidad espaciotemporal sea destruida.

Sin embargo, una sugerencia alternativa,^[3.49] frecuentemente aducida, propone que de algún modo se ha estado produciendo una «fuga» de información desde mucho tiempo antes, codificada en lo que se conoce como «entrelazamientos cuánticos», que se expresarían en correlaciones sutiles en la radiación de Hawking procedente del agujero. Desde este punto de vista, la radiación de Hawking no sería exactamente «térmica» (o «aleatoria»), sino que la información completa que parecería haberse perdido irrecuperablemente en la singularidad se tiene plenamente en cuenta (¿repetida?) fuera del agujero. Una vez más tengo serias dudas sobre estas sugerencias. De acuerdo con propuestas de este tipo, cualquier información que llega a la vecindad de la singularidad debe de algún modo estar «repetida» o «copiada» en esta información entrelazada externa, lo que en sí mismo violaría principios cuánticos básicos.^[3.50]

Además, en su argumento original de 1974,^[3.51] que demostraba la presencia de radiación térmica emanando de un agujero negro, Hawking hacía uso explícito del hecho de que la información incidente, en la forma de una onda de prueba, tendría que estar compartida entre la que escapa del agujero y la que cae en él. Es precisamente la hipótesis de que la parte que cae en el agujero negro se pierde irrecuperablemente la que lleva a la conclusión de que lo que sale debe tener un carácter térmico, con una temperatura que es precisamente igual a la que ahora llamamos temperatura de Hawking. Este argumento depende del uso del diagrama conforme de la Fig. 2.38(a), que para mí deja manifiestamente claro que la información incidente está realmente compartida entre la que cae en el agujero y la que escapa al infinito, y la que cae en el agujero se pierde, que es una parte esencial de la discusión. De hecho, durante muchos años el propio Hawking ha sido uno de los más fuertes defensores del punto de vista de que la información se pierde realmente en los agujeros negros. Pero en la XVII Conferencia Internacional sobre Relatividad General y Gravitación, celebrada en Dublín en 2004, Hawking anunció que había cambiado de opinión y, reconociendo públicamente que había perdido una apuesta que él (y Kip Thorne) había hecho con John Preskill, argumentó que había estado equivocado y que ahora creía^[3.52] que toda la información debe ser recuperada fuera del agujero. Ciertamente mi opinión personal es que Hawking debería haberse quedado en sus trece, y que su punto de vista anterior estaba mucho más próximo a la verdad.

Sin embargo, la opinión revisada de Hawking está mucho más en consonancia con lo que podría considerarse el punto de vista «convencional» entre los teóricos de campos cuánticos. De hecho, la destrucción real de la información física no es algo que atraiga a la mayoría de los físicos, y la idea de que la información pueda destruirse de esta forma en un agujero negro es frecuentemente llamada la «paradoja de la información del agujero negro». La razón principal por la que los físicos tienen problemas con esta pérdida de información es que ellos mantienen la fe en que una adecuada descripción por gravedad cuántica del destino de un agujero negro debería ser consistente con uno de los principios fundamentales de la teoría cuántica conocido como evolución unitaria, que es básicamente una evolución determinista de un sistema cuántico simétrica respecto al tiempo,^[3.53] como la gobernada por la ecuación de Schrödinger. Por su propia naturaleza, la información no puede perderse en el proceso de evolución unitaria, debido a la reversibilidad de ésta. Por ello, la pérdida de información que parece ser un ingrediente necesario de la evaporación de agujeros negros de Hawking es, de hecho, incompatible con la evolución unitaria.

No puedo entrar aquí en los detalles de la teoría cuántica,^[3.54] pero una breve mención de las ideas rudimentarias será importante para mi argumentación posterior. La expresión matemática básica de un sistema cuántico en un instante concreto viene dada por el estado cuántico o función de onda del sistema, para la que se suele utilizar la letra ψ. Como ya se ha mencionado, el estado cuántico ψ dejado a sí mismo evoluciona en el tiempo de acuerdo con la ecuación de Schrödinger; esta evolución unitaria es un proceso continuo determinista y básicamente simétrico respecto al tiempo para el que utilizo la letra U. Sin embargo, para determinar qué valor podría haber alcanzado un parámetro observable q en un instante dado t, se aplica a ψ un proceso matemático completamente diferente, que se conoce como realizar una observación, o medida. Ésta se describe en términos de cierta operación que se aplica a ψ y nos proporciona un conjunto de alternativas posibles ψ₁, ψ₂, ψ₃, ψ₄, …, una por cada uno de los posibles resultados q₁, q₂, q₃, q₄, … para el parámetro q escogido, y con probabilidades respectivas P₁, P₂, P₃, P₄, … para estos resultados. Este conjunto de alternativas, con sus correspondientes probabilidades, está determinado por y ψ por un procedimiento matemático especificado. Para reflejar lo que realmente parece suceder en el mundo físico, bajo medida, encontramos que ψ simplemente salta a una de las alternativas ψ₁, ψ₂, ψ₃, ψ₄, … del conjunto dado, digamos a ψ_j, y esta elección parece ser completamente aleatoria, aunque con una probabilidad dada por la correspondiente P_j. Este reemplazamiento de ψ por la elección particular ψ_j que hace la naturaleza se conoce como reducción del estado cuántico o colapso de la función de onda, para el que utilizo la letra R. Tras esta medida, que ha hecho que ψ salte (a ψ_j), la nueva función de onda ψ_j procede de nuevo de acuerdo con U hasta que se hace una nueva medida, y así sucesivamente.

Lo que es particularmente extraño en la mecánica cuántica es este mismo curioso híbrido, por el que el comportamiento del estado cuántico parece alternar entre estos dos procedimientos matemáticos completamente diferentes: el continuo y determinista U, y el discontinuo y probabilista R. No es sorprendente que los físicos no se sientan felices con este estado de cosas, y que por ello adopten una u otra entre varias posturas filosóficas diferentes. Hay noticia (referida por Heisenberg) de que el propio Schrödinger dijo: «Si este condenado salto cuántico estuviera aquí para quedarse, lamentaría haber estado implicado en la teoría cuántica».^[3.55] Otros físicos, plenamente conscientes de la gran contribución que hizo Schrödinger con el descubrimiento de su ecuación de evolución, y aun compartiendo su disgusto por el «salto cuántico», se distanciarían de su postura diciendo que todavía no había salido a la luz toda la historia de la evolución cuántica. De hecho, una idea común es que la historia completa está contenida de algún modo dentro de U, junto con una adecuada «interpretación» del significado de ψ; y que de algún modo R emergerá de todo esto, quizá porque el verdadero «estado» incluye no solo el sistema cuántico en consideración, sino también su complicado entorno, incluido el aparato de medida, o quizá porque nosotros mismos, los observadores últimos, somos parte de un estado que evoluciona de forma unitaria.

No quiero entrar en todas las alternativas u opiniones que aún enturbian la cuestión U/R, sino simplemente afirmar mi propia postura, que básicamente se alinea con el propio Schrödinger, y con Einstein, y quizá más sorprendentemente con Dirac,^[3.56] a quien debemos la formulación general de la mecánica cuántica actual,^[3.57] y adoptar el punto de vista de que la mecánica cuántica actual es una teoría provisional. Y esto pese a todas las predicciones de la teoría maravillosamente confirmadas y la gran amplitud de los fenómenos observados que explica, sin que halla en contra una sola observación. Más en concreto, mi idea es que el fenómeno R representa una desviación respecto de la adhesión estricta de la naturaleza a la unitariedad, y que esto surge cuando la gravedad empieza a intervenir seriamente (aunque sutilmente).^[3.58] De hecho, hace tiempo que soy de la opinión de que la pérdida de información en los agujeros negros, y la consiguiente violación de U, representa una parte poderosa del argumento de que una estricta adhesión a U no puede ser parte de la verdadera (aún no descubierta) teoría cuántica de la gravedad.

Creo que es esto lo que contiene la clave para la solución del enigma al que nos enfrentábamos al inicio de esta sección. Estoy pidiendo al lector que acepte que la pérdida de información en los agujeros negros —y la consiguiente violación de la unitariedad— es no solo plausible, sino una realidad necesaria en las situaciones en consideración. Debemos reexaminar la definición de entropía de Boltzmann en el contexto de la evaporación de agujeros negros. ¿Qué significa realmente la «pérdida de información» en la singularidad? Una mejor manera de describirla es como una pérdida de grados de libertad, de modo que algunos de los parámetros que describen el espacio de fases han desaparecido y el espacio de fases se ha hecho realmente más pequeño que lo que era antes. Éste es un fenómeno completamente nuevo cuando se está considerando el comportamiento dinámico. De acuerdo con la idea normal de evolución dinámica, descrita en §1.3, el espacio de fases es algo fijo, y la evolución dinámica está descrita por un punto que se mueve en dicho espacio de fases fijo; pero cuando la evolución dinámica incluye una pérdida de grados de libertad en alguna etapa, como parece ser aquí el caso, ¡el espacio de fases se contrae como parte de la descripción de esta evolución! En la Fig. 3.14 he tratado de ilustrar cómo se describiría este proceso, utilizando un análogo en baja dimensión.

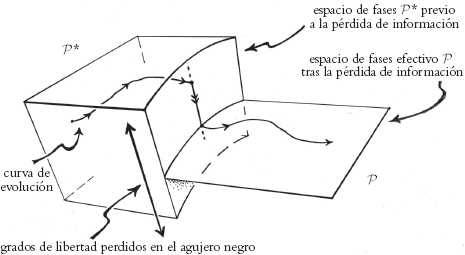
Fig. 3.14. Evolución en el espacio de fases tras la pérdida de información en un agujero negro.

En el caso de la evaporación de un agujero negro, éste es un proceso muy sutil, y no deberíamos pensar que esta contracción tiene lugar «repentinamente» en algún instante concreto (por ejemplo, en el «pop»), sino inadvertidamente. Todo esto está ligado al hecho de que, en relatividad general, no hay un único «tiempo universal», y esto tiene una relevancia especial en el caso de un agujero negro, donde la geometría espaciotemporal se desvía mucho de la homogeneidad espacial. Esto queda muy bien ilustrado en la imagen del colapso de Oppenheimer-Snyder (§2.4, véase la Fig. 2.24) con evaporación de Hawking final (§2.5, véanse las Figs. 2.40 y 2.41), donde en la Fig. 3.15(a) y su diagrama conforme estricto Fig. 3.15(b) he dibujado con líneas continuas una familia de 3-superficies de tipo espacio (secciones a tiempo constante) donde toda la información perdida en el agujero parece desaparecer en el instante del «pop», mientras que con líneas de trazos he dibujado una familia diferente de 3-superficies de tipo espacio para las que la información parece desaparecer gradualmente, extendida sobre toda la historia de la existencia del agujero negro. Aunque las imágenes se refieren estrictamente a simetría esférica, siguen aplicándose de una manera esquemática mientras se suponga censura cósmica fuerte (excepto, por supuesto, en el propio pop).

Esta indiferencia respecto a cuándo tiene lugar realmente la pérdida de información sirve para resaltar el hecho de que su desaparición no tiene ningún efecto en la (termo)dinámica externa, y podemos adoptar el punto de vista de que la Segunda Ley procede de acuerdo con su práctica normal, donde la entropía continúa en aumento, aunque debemos ser cuidadosos acerca de a qué noción de «entropía» nos estamos refiriendo. Esta entropía se refiere a todos los grados de libertad, incluidos los del material que ha caído en los agujeros. Sin embargo, los grados de libertad que se refieren a lo que ha caído dentro tendrán que enfrentarse más pronto o más tarde a la singularidad y, de acuerdo con las consideraciones anteriores, se perderán para el sistema. Cuando el agujero negro haya desaparecido con un pop, debemos tener radicalmente reducida la escala de nuestro espacio de fases de modo que, como sucede cuando se devalúa la moneda de un país, los volúmenes del espacio de fases contarán, en general, mucho menos que lo hacían antes, aunque esta enorme devaluación no será advertida por la física local que continúa alejada del agujero en cuestión. Debido al logaritmo en la fórmula de Boltzmann, este escalado a la baja de los volúmenes sería equivalente a restar una gran constante de la entropía global del universo externo al agujero negro en cuestión.

Fig. 3.15. Un agujero negro en evaporación de Hawking: (a) imagen espaciotemporal convencional; (b) diagrama conforme estricto. Puede considerarse que la pérdida de grados de libertad internos desaparece solo cuando ocurre el «pop», que es la imagen sugerida de acuerdo con las secciones espaciotemporales dadas por líneas continuas. Alternativamente, de acuerdo con las secciones espaciotemporales dadas por las líneas de trazos, la pérdida ocurre gradualmente durante toda la historia del agujero negro.

Podemos comparar esto con la discusión al final de §1.3, donde se ha señalado que el logaritmo en la fórmula de Boltzmann es lo que da lugar a la aditividad de la entropía para sistemas independientes. En la argumentación precedente, la entropía engullida y finalmente destrozada por el agujero negro desempeña el papel de la parte externa del sistema en consideración en §1.3, con parámetros que definen el espacio de fases externo que se refería a la galaxia Vía Láctea externa al laboratorio, mientras que aquí se refiere a los agujeros negros. Véase la Fig. 3.16. Lo que ahora estamos tomando como el mundo exterior a los agujeros negros, en el que podríamos imaginar que se está realizando un experimento, corresponde, en la exposición de §1.3 (Fig. 1.9), a la parte interna del sistema, que define el espacio de fases . De la misma manera que la eliminación de grados de libertad en la Vía Láctea de §1.3 (cuando algunos de ellos fueran absorbidos en el agujero central de la galaxia) no supondría ninguna diferencia para las consideraciones de entropía en el experimento que se está realizando, tampoco la destrucción de información en agujeros negros a lo largo del universo, finalizada cuando cada uno de ellos desaparezca individualmente con su pop, produce ninguna violación efectiva de la Segunda Ley, ¡lo que es compatible con lo que ya se ha resaltado en esta sección!

Sin embargo, el volumen del espacio de fases del universo en conjunto quedaría muy drásticamente reducido por esta pérdida de información,^[3.59] y esto es básicamente lo que necesitamos para la resolución del enigma planteado al principio de esta sección. Es un tema sutil, y deben satisfacerse muchas cuestiones detalladas de consistencia para que la reducción de volumen del espacio de fases sea la adecuada para lo que se requiere para la CCC. En términos generales, esta consistencia no parece irrazonable, puesto que cabe esperar que el incremento de entropía global que experimente nuestro actual eón a lo largo de toda su historia sea mediante la formación (y evaporación) de agujeros negros. Aunque no es enteramente obvio para mí cómo se calcula, con cualquier grado de precisión, la reducción efectiva de entropía debida a la pérdida de información, una buena conjetura sería estimar la entropía de Bekenstein-Hawking de los tamaños máximos que habrían alcanzado los agujeros negros si no hubiera habido pérdida en forma de radiación de Hawking, y considerar que la totalidad de esta entropía da la necesaria escala de reducción en el espacio de fases disponible para el inicio del eón siguiente. Evidentemente hay muchas cuestiones que necesitan un estudio más detallado para que podamos estar seguros de que la CCC sea viable a este respecto. Pero no puedo ver ninguna razón para pensar que CCC sea contradicha por tales consideraciones.

Fig. 3.16. La pérdida de información en agujeros negros no afecta al espacio de fases local (compárese con la Fig. 1.9), aunque contribuye al total, antes de perderse.