2.4. Agujeros negros y singularidades espaciotemporales

En muchas situaciones físicas, donde los efectos de la gravedad son relativamente pequeños, los conos nulos se desvían solo ligeramente de sus localizaciones en el espacio de Minkowski . Sin embargo, en el caso de un agujero negro encontramos una situación muy diferente, como he intentado señalar en la Fig. 2.24. Esta imagen del espaciotiempo representa el colapso de una estrella supermasiva (quizá con 10 o más veces la masa del Sol) que, tras haber agotado sus fuentes de energía (nuclear) interna, colapsa de manera imparable hacia dentro. En una cierta etapa (que puede identificarse como el momento en que la velocidad de escape^[2.34] de la superficie de la estrella alcanza la velocidad de la luz), la inclinación hacia dentro de los conos nulos se hace tan extrema que la parte más exterior del cono futuro se hace vertical en el diagrama. Trazando la envolvente de estos conos concretos localizamos la 3-superficie conocida como horizonte de sucesos, dentro del que se encuentra en caída el cuerpo de la estrella. (Por supuesto, al dibujar esta figura he tenido que suprimir una de las dimensiones espaciales, de modo que el horizonte aparece como una 2-superficie ordinaria, pero esto no debería confundir al lector).

Debido a esta inclinación en los conos nulos, encontramos que la línea de universo de cualquier partícula o señal luminosa que tiene su origen dentro del horizonte de sucesos no podrá escapar al exterior, pues para cruzar el horizonte tendría que violar los requisitos de §2.3. Además, si seguimos hacia atrás (en el tiempo) un rayo de luz que entra en el ojo de un observador externo situado a una distancia segura del agujero, mirando hacia este, encontramos que este rayo no puede cruzar hacia atrás el horizonte de sucesos y pasar a su interior, sino que se queda suspendido precisamente sobre la superficie, para encontrar el cuerpo de la estrella tan solo un instante antes de que éste se sumerja por debajo del horizonte. Tal sería el caso en teoría, con independencia de cuánto espere el observador externo (es decir, independientemente de cuán alto en la figura colocamos el ojo del observador), pero en la práctica la imagen percibida por el observador se desplazaría fuertemente hacia el rojo y desaparecería de la vista tanto más rápido cuanto más tarde en el tiempo esté situado el obervador, de modo que en poco tiempo la imagen de la estrella se volvería oscura, de acuerdo con la terminología «agujero negro».

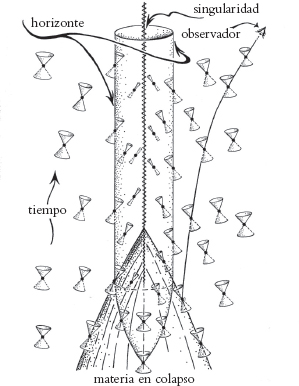
Fig. 2.24. Colapso de una estrella supermasiva para dar un agujero negro. Cuando la inclinación hacia dentro del cono de luz futuro se hace vertical, la luz procedente de la estrella ya no puede escapar de su gravedad. La envolvente de estos conos es el horizonte de sucesos.

Una pregunta natural que hay que plantear es: ¿cuál es el destino de esta materia de la estrella que cae hacia dentro una vez que ha cruzado el horizonte? ¿Sería posible que disfrute de una complicada actividad posterior, quizá arremolinándose, cuando se acerca al centro, y que esto la lleve a rebotar hacia fuera? El modelo original para tal colapso, como el de la Fig. 2.24, fue propuesto por J. Robert Oppenheimer y su discípulo Hartland Snyder en 1939, y fue presentado como una solución exacta de las ecuaciones de Einstein. Sin embargo, ellos tuvieron que hacer varias hipótesis simplificadoras para poder representar su solución de una manera explícita. La más importante (y más restrictiva) de esas hipótesis era suponer que había simetría esférica exacta, lo que excluía un «arremolinamiento» asimétrico. Ellos suponían también que la naturaleza del material de la estrella podía aproximarse razonablemente bien como un fluido sin presión, lo que los teóricos de la relatividad conocen como «polvo» (véase también §2.1). Lo que encontraron Oppenheimer y Snyder, bajo estas hipótesis, es que el colapso hacia dentro simplemente continúa hasta que la densidad del material se hace infinita en un punto en el centro, y en consecuencia la curvatura espaciotemporal correspondiente también se hace infinita. Por ello, este punto central, en su solución —representada por la línea ondulada vertical en el centro de la Fig. 2.24— se conoce como una singularidad espaciotemporal, donde la teoría de Einstein «se retira» y la física estándar no nos ofrece ninguna manera de desarrollar más la solución.

La presencia de tales singularidades espaciotemporales ha planteado a los físicos un enigma fundamental, a menudo visto como el problema inverso al del Big Bang origen del universo. Mientras que el Big Bang se ve como el comienzo del tiempo, las singularidades en agujeros negros se presentan como una representación del fin del tiempo, al menos en lo que concierne al destino de ese material que, en alguna etapa, ha caído dentro del agujero. En este sentido podemos considerar el problema que presentan las singularidades de agujero negro como el inverso temporal del que presenta el Big Bang.

Es cierto que, en la imagen de colapso de agujero negro de la Fig. 2.24, toda curva causal que tiene su origen dentro del horizonte debe terminar en la singularidad central cuando se extiende al futuro todo lo posible. Análogamente, en cualquiera de los modelos de Friedmann mencionados en §2.1, toda curva causal (en el modelo entero), si se extiende hacia el pasado, debe terminar (en realidad originarse) en la singularidad del Big Bang. Por consiguiente, podría parecer (aparte de que el caso del agujero negro es más local) que las dos situaciones son, en efecto, la inversa temporal una de otra. Pese a ello, nuestras consideraciones de la Segunda Ley podrían muy bien sugerirnos que no puede ser así. El Big Bang debe ser algo de entropía extraordinariamente baja en comparación con la que encontramos en un agujero negro. Y la diferencia entre una y la inversa temporal de la otra debe ser una cuestión clave para nuestras consideraciones.

Antes de que lleguemos (en §2.6) a la naturaleza de esta diferencia, hay que afrontar una importante cuestión preliminar. Debemos abordar la cuestión de si, o en qué medida, tenemos razones para confiar en los modelos: el de Oppenheimer y Snyder, por un lado, y los modelos cosmológicos altamente simétricos tales como el de Friedmann, por otro. Debemos señalar dos de las importantes hipótesis subyacentes a la imagen de Oppenheimer-Snyder del colapso gravitatorio. Éstas son la simetría esférica y la idealización particular del material que constituye el cuerpo colapsante que se considera totalmente libre de presión. Estas dos hipótesis se aplican también a los modelos cosmológicos de Friedmann (la simetría esférica se aplica a todos los modelos FLRW), de modo que quizá tengamos motivos para dudar de que estos modelos representen necesariamente el comportamiento inevitable de la materia que colapsa (o que explota) en situaciones tan extremas, según la relatividad general de Einstein.

De hecho, ambas cuestiones eran materias que me interesaban cuando empecé a pensar seriamente sobre el colapso gravitatorio en el otoño de 1964. Este interés había sido estimulado por las conversaciones que mantuve con el profundamente intuitivo físico estadounidense John A. Wheeler, tras el descubrimiento por Maarten Schmidt de un sorprendente objeto^[2.35] cuyos extraordinarios brillo y variabilidad indicaban que en ello podría estar implicado algo que se acercaba a lo que ahora llamamos un «agujero negro». En esa época era creencia común, basada en un detallado trabajo teórico realizado por dos físicos rusos, Evgeni Mijáilovich Lifshitz e Isaak Markovich Jalatnikov, que en la situación general, en ausencia de condiciones de simetría, no aparecerían singularidades espaciotemporales en un colapso gravitatorio general. Siendo solo vagamente conocedor del trabajo ruso, pero teniendo dudas de que el tipo de análisis matemático que ellos habían utilizado pudiera llevar a una conclusión definitiva sobre esta materia, empecé a pensar en el problema a mi propia manera más geométrica. Para ello tenía que tratar de entender varios aspectos globales acerca de cómo se propagan los rayos de luz, cómo podrían ser concentrados por la curvatura espaciotemporal, y qué tipo de superficies singulares podrían aparecer cuando empiezan a retorcerse y cruzarse unos con otros.

Yo ya había pensando en estos términos a propósito del modelo de estado estacionario del universo, mencionado al principio de §2.2. Me gustaba mucho ese modelo, aunque no tanto como me había gustado la relatividad general de Einstein —con su grandiosa unificación de nociones geométricas básicas del espacio-tiempo con principios físicos fundamentales—, así que me preguntaba si habría alguna posibilidad de que ambos pudieran hacerse compatibles. Si uno se atiene al puro modelo de estado estacionario suavizado, se ve forzado enseguida a concluir que esta compatibilidad no puede conseguirse sin la introducción de densidades de energía negativas, que tienen el efecto, en la teoría de Einstein, de poder separar rayos de luz para contrarrestar el implacable efecto de curvatura hacia dentro de la densidad de energía positiva de la materia normal (véase §2.6). En general, la presencia de energía negativa en sistemas físicos es una «mala noticia», pues es probable que lleve a inestabilidades incontrolables. Por ello me preguntaba si las desviaciones de la simetría permitirían evitar estas conclusiones desagradables. Sin embargo, los argumentos globales que pueden utilizarse para abordar el comportamiento topológico de tales superficies de rayos luminosos resultan ser tan potentes, si se toman con el debido cuidado, que frecuentemente pueden aplicarse en situaciones muy generales para deducir conclusiones del mismo tipo a las que se llega cuando sí se supone esta alta simetría. El resultado era (aunque nunca publiqué estas conclusiones) que desviaciones razonables de la simetría no sirven de ayuda, y por eso el modelo de estado estacionario, incluso cuando se admiten desviaciones considerables del modelo suavizado simétrico, no puede dejar de ser incompatible con la relatividad general a menos que estén presentes energías negativas.

Yo también había utilizado algunos argumentos del mismo tipo para investigar las diferentes posibilidades que pueden surgir cuando se considera el futuro remoto de sistemas gravitatorios. Las técnicas a las que me vi llevado, que incluían las ideas de geometría espaciotemporal conforme (mencionadas ya en §2.3, y que desempeñarán papeles importantes en la Parte 3), también me llevaron a considerar las propiedades de focalización de sistemas de rayos luminosos^[2.36] en situaciones generales, así que empecé a pensar que me sentía muy cómodo con esas cosas y dirigí mi atención a la cuestión del colapso gravitatorio. La principal dificultad adicional era que se necesitaba algún tipo de criterio para caracterizar situaciones en las que el colapso había rebasado un «punto de no retorno», pues hay muchas situaciones en las que el colapso de un cuerpo puede volverse del revés porque las fuerzas de presión se hacen suficientemente grandes para invertir un colapso, de modo que el material «rebota». Este punto de no retorno aparece cuando se forma el horizonte, puesto que entonces la gravitación se ha hecho tan intensa que ha superado a cualquier otra cosa. Sin embargo, la presencia y localización del horizonte resulta algo difícil de especificar matemáticamente, pues su definición precisa requiere que el comportamiento sea examinado en todo su recorrido hasta el infinito. Por consiguiente, fue una suerte para mí que me viniera a la cabeza una idea^[2.37] —la de una «superficie atrapada»— de un carácter más local,^[2.38] cuya presencia en un espacio-tiempo puede tomarse como condición de que ha tenido lugar un colapso gravitatorio imparable.

Mediante el uso de un argumento del tipo «rayo luminoso/topología» que había estado desarrollando fui entonces capaz de establecer un teorema^[2.39] según el cual, cuando quiera que ha tenido lugar un colapso gravitatorio, no pueden evitarse las singularidades, con tal de que el espacio-tiempo satisfaga un par de condiciones «razonables». Una de ellas es que la focalización de los rayos luminosos nunca puede ser negativa; en términos más físicos esto significa que si se aceptan las ecuaciones de Einstein (con o sin la presencia de una constante cosmológica Λ), el flujo de energía a través de un rayo de luz nunca es negativo. Una segunda condición es que el sistema completo debe poder evolucionar a partir de una 3-superficie abierta (es decir, lo que se denomina «no compacta») de tipo espacio Σ. Ésta es una condición muy habitual cuando se considera una situación razonablemente localizada (es decir, no cosmológica) que evoluciona físicamente. Desde el punto de vista geométrico, todo lo que demandamos es que cualquier curva causal, dirigida hacia el futuro de Σ, en el espacio-tiempo en consideración, debe cortar a Σ cuando se prolonga hacia atrás (en el tiempo) todo lo posible (véase la Fig. 2.25). El único requisito adicional (aparte de la supuesta existencia de una superficie atrapada) concierne a lo que realmente va a entenderse por una «singularidad» en este contexto. Básicamente, una singularidad representa simplemente un obstáculo a continuar el espacio-tiempo suave e indefinidamente hacia el futuro,^[2.40] lo que es consistente con la hipótesis que se acaba de hacer.

Fig. 2.25. Una «superficie de Cauchy» inicial; cualquier punto p en su futuro tiene la propiedad de que toda curva causal que termina en p, cuando se extiende hacia atrás hasta un pasado suficientemente lejano, debe cortar a la superficie.

La fuerza de este resultado reside en su generalidad. No sólo no se requiere ninguna hipótesis de simetría, ni ninguna otra condición simplificadora que pudiera hacer las ecuaciones más fáciles de resolver, sino que la única restricción impuesta a la naturaleza de la fuente material del campo gravitatorio es que sea «físicamente razonable» de acuerdo con el requisito físico de que el flujo de energía de este material a través de cualquier rayo luminoso nunca debe ser negativo, una condición conocida como la «condición de energía débil». Esta condición es ciertamente satisfecha por el polvo libre de presión supuesto por Oppenheimer y Snyder, y también por Friedmann. Pero es mucho más general que esto, e incluye todo tipo de material clásico físicamente realista que consideran los teóricos de la relatividad.

No obstante, frente a esta fuerza, la debilidad de este resultado reside en que no nos dice casi nada sobre la naturaleza detallada del problema al que se enfrenta nuestra estrella en colapso. No da ninguna clave sobre la forma geométrica de la singularidad. Ni siquiera nos dice que la materia alcanzará una densidad infinita o que la curvatura del espacio-tiempo se hará infinita en cualquier otro modo. Más aún, ni siquiera nos dice nada sobre dónde empezará a manifestarse el comportamiento singular.

Para abordar tales cuestiones se necesita algo mucho más en la línea del análisis detallado de los físicos rusos Lifshitz y Jalatnikov antes mencionado. ¡Pero el teorema que yo había encontrado en los últimos meses de 1964 parecía estar en conflicto directo con lo que ellos habían afirmado previamente! De hecho era así, y en los meses siguientes hubo mucha consternación y confusión. Sin embargo, todo quedó resuelto cuando los rusos, con la ayuda de un joven colega, Vladimir A. Belinski, fueron capaces de localizar y luego corregir un error en su trabajo anterior. Mientras que originalmente había parecido que las soluciones singulares de las ecuaciones de Einstein eran casos muy especiales, el trabajo corregido coincidía con el resultado que yo había obtenido, lo que demostraba que el comportamiento singular era realmente el caso general. Además, el trabajo de Belinski-Jalatnikov-Lifshitz proporcionaba un argumento plausible a favor de un tipo de actividad caótica extraordinariamente complicada para la aproximación a una singularidad, ahora conocido como la conjetura BKL. Tal comportamiento ya había sido anticipado a partir de consideraciones del teórico relativista estadounidense Charles W. Misner —conocidas como el universo mezclador— y creo que es muy probable que, al menos en una amplia clase de situaciones posibles, esta actividad «mezcladora» incontrolada y caótica sea el caso general.

Más adelante (en §2.6) tendré más cosas que decir sobre esta materia, pero por ahora debemos abordar otra cuestión, a saber, si es realmente probable que algo parecido a una superficie atrapada aparezca en cualquier situación plausible. La razón original para anticipar que estrellas supermasivas puedan colapsar realmente de forma catastrófica en una etapa tardía de su evolución surgió del trabajo de Subrahmanyan Chandrasekhar, en 1931, cuando estudió las estrellas muy pequeñas y enormemente densas conocidas como enanas blancas (de las que el primer ejemplo conocido era la misteriosa compañera oscura de la estrella brillante Sirio), de masa comparable a la del Sol pero de un radio aproximadamente igual al de la Tierra. Las enanas blancas se sostienen por la presión de degeneración electrónica, un principio mecanocuántico que impide que los electrones se amontonen unos sobre otros. Chandrasekhar demostró que cuando se incorporan los efectos de la relatividad (especial), hay un límite a la masa que se puede sostener frente a la gravedad de esta manera, y él dirigió la atención al profundo enigma que esto plantea para masas frías mayores que este «límite de Chandrasekhar». Este límite es de aproximadamente 1,4 Mʘ (donde Mʘ denota la masa del Sol).

La evolución de una estrella ordinaria (de la «secuencia principal») como nuestro Sol incluye una etapa tardía donde sus capas externas se hinchan, de modo que se convierte en una enorme gigante roja, acompañada por un núcleo de electrones degenerados. Este núcleo acumula cada vez más material de la estrella, y si esta acumulación no supera el límite de Chandrasekhar, la estrella entera puede terminar como una enana blanca, que finalmente se enfría hasta terminar su existencia como una enana negra. Éste es de hecho el destino que espera a nuestro propio Sol. Pero para estrellas mucho más grandes, el núcleo de enana blanca podría colapsar en alguna etapa, debido a que se ha superado el límite de Chandrasekhar, y el material que cae en la estrella lleva a una explosión de supernova en extremo violenta (que probablemente supera en brillo, durante algunos días, a la galaxia entera en la que reside). Durante este proceso podría ser expulsado material suficiente para que el núcleo resultante pueda sostenerse a una densidad incluso mucho mayor (con, digamos, 1,5 Mʘ comprimidas en una región de aproximadamente 10 km de diámetro), formando una estrella de neutrones, que se sostiene por presión de degeneración neutrónica.

Las propias estrellas de neutrones se manifiestan a veces como púlsares (véase §2.1 y la nota 2.6) y muchos han sido observados ahora en nuestra galaxia. Pero de nuevo hay un límite para la masa posible de una estrella semejante, que es de unas 1,5 Mʘ (a veces llamado límite de Landau). Si la estrella original hubiera sido suficientemente masiva (digamos más de 10 Mʘ), es muy probable que en la explosión no se expulsara un material suficiente, y el núcleo sería incapaz de sostenerse como una estrella de neutrones. Entonces no queda nada que pueda detener su colapso, y con toda probabilidad se alcanzaría una etapa en la que aparece una superficie atrapada.

Por supuesto, ésta no es una conclusión definitiva, y muy bien se podría argumentar que no se conoce lo suficiente sobre la física de estados tan extraordinariamente condensados como los que alcanzaría el material antes de que se alcance el régimen de superficie atrapada (aunque sólo sea en un factor de aproximadamente 3 en el radio, por debajo del de una estrella de neutrones). Sin embargo, el argumento para la aparición de agujeros negros es considerablemente más fuerte si consideramos concentraciones de masa en la escala mucho mayor de conjuntos de muchas estrellas cerca de los centros galácticos. Esto es una simple cuestión de cómo escalan las cosas. Para sistemas cada vez mayores, las superficies atrapadas aparecerían a densidades cada vez menores. Por ejemplo, en una región de 10⁶ kilómetros de diámetro hay lugar suficiente para un millón de estrellas enanas blancas, sin que ninguna de ellas tenga que estar en contacto con otra, y esto sería suficientemente pequeño para que a su alrededor aparezca una superficie atrapada. La cuestión de la «física desconocida» a densidades extremadamente altas no es en realidad la cuestión relevante cuando se trata de la formación de agujeros negros.

Hay otra cuestión teórica que he pasado por alto hasta ahora. He estado suponiendo tácitamente que la existencia de una superficie atrapada implica que se formará un agujero negro. Sin embargo, esta deducción depende de lo que se conoce como «censura cósmica» que, aunque la creencia general la da por cierta, hoy por hoy sigue siendo una conjetura no probada.^[2.41] Junto con la conjetura BKL, es probablemente la mayor cuestión no resuelta en relatividad general clásica. Lo que afirma la censura cósmica es que no ocurren singularidades espaciotemporales desnudas en colapsos gravitatorios genéricos, donde «desnudas» significa que curvas causales que tienen su origen en la singularidad pueden escapar hasta llegar a un observador externo distante (de modo que la singularidad no está protegida de la observación externa por un horizonte de sucesos). Volveré a esta cuestión de la censura cósmica en §2.6.

En cualquier caso, la situación observacional en el momento actual está a favor de la presencia de agujeros negros. Las pruebas a favor de que algunos sistemas de estrellas binarias contienen agujeros negros de unas pocas masas solares son bastante impresionantes, aunque son de carácter «negativo»: la presencia de una componente invisible se deja notar por movimientos dinámicos en el sistema, y la masa de dicha componente invisible es considerablemente mayor que la que podría tener cualquier objeto compacto, según la teoría estándar. Las pruebas más impresionantes de este tipo se dan cuando se observan los movimientos orbitales muy rápidos de estrellas alrededor de un ente invisible pero enormemente masivo y compacto en el centro de nuestra Vía Láctea. La velocidad de estos movimientos es tal que esta entidad ¡debe tener una masa de unos 4.000.000 Mʘ! Es difícil imaginar que esto pueda ser otra cosa que un agujero negro. Además de las pruebas de este tipo «negativo», se observan también entidades de esta naturaleza que están atrayendo material circundante, sin que haya evidencia de que dicho material excite una «superficie» en la entidad. La falta de una superficie ponderable es una prueba clara y directa de un agujero negro.^[2.42]