2.5. Diagramas conformes y fronteras conformes

Hay una forma conveniente de representar modelos espaciotemporales en su totalidad, especialmente en el caso de modelos que poseen simetría esférica, como sucede en el caso de los espacio-tiempos de Oppenheimer-Snyder y de Friedmann. Es mediante el uso de diagramas conformes. Distinguiré aquí dos tipos de diagramas conformes: los diagramas conformes estrictos y los esquemáticos.^[2.43] Veamos la utilidad de cada uno.

Empecemos con los diagramas conformes estrictos, que pueden utilizarse para representar espacio-tiempos (aquí denotados por ) con simetría esférica exacta. El diagrama sería una región del plano, y cada punto en el interior de representaría el equivalente a una superficie esférica completa (es decir, un equivalente a S²) de puntos de . Para hacernos una imagen de lo que sucede, podemos perder una dimensión espacial e imaginar que rotamos la región respecto a una línea vertical a la izquierda (véase la Fig. 2.26), que se conoce como un eje de rotación. Entonces cada punto en describirá un círculo (S¹). Esto es suficientemente bueno para nuestra imaginación visual. Pero para la plena imagen 4-dimensional de nuestro espacio-tiempo , necesitaríamos una rotación 2-dimensional, de modo que cada punto interior de tiene que describir una superficie esférica (S²) en .

A menudo, en nuestros diagramas conformes estrictos encontramos que tenemos un eje de rotación que es parte de la frontera para la región . Entonces, cada uno de esos puntos frontera en el eje —representados en el diagrama como una línea de trazos— representaría un único punto (y no un S²) en el espacio-tiempo 4-dimensional, de modo que toda la línea de trazos también representaría una única línea en . La Fig. 2.27 nos da una idea de cómo está constituido el espacio-tiempo entero como una familia de espacios 2-dimensionales idénticos a en rotación alrededor del eje que es ahora la línea de trazos.

Fig. 2.26. Diagrama conforme estricto utilizado para representar espacio-tiempos (aquí denotados por ) con simetría esférica exacta. La región 2-dimensional está rotada (a través de una esfera 2-dimensional S²) para formar el 4-espacio .

Fig. 2.27. La línea de trazos en la frontera de es un eje de simetría; cada punto del eje representa un único punto del espacio-tiempo, y no un S².

Fig. 2.28. Los «conos nulos» en , a un ángulo de 45° respecto a la vertical, son las intersecciones de los conos en con un insertado.

Vamos a considerar como un espacio-tiempo conforme, sin preocuparnos demasiado por el escalado particular que da a su métrica completa g. Entonces, de acuerdo con la frase que cerraba §2.3, está dotado de una familia completa de conos nulos (orientados en el tiempo). De acuerdo con esto, el propio , al ser un subespacio 2-dimensional de , hereda de este una estructura espaciotemporal conforme 2-dimensional, y tiene sus propios «conos nulos orientados en el tiempo». Estos consisten simplemente en un par de direcciones «nulas» distintas en cada punto de que se estiman orientadas hacia el futuro. (Son simplemente las intersecciones de los planos que definen las copias de con los conos nulos futuros de ; véase la Fig. 2.28.)

En un diagrama conforme estricto nos proponemos disponer todas estas direcciones nulas futuras en para que estén orientadas a 45° respecto a la vertical. Para ilustrar la situación, he dibujado, en la Fig. 2.29, un diagrama conforme para el espacio-tiempo de Minkowski entero , con las líneas nulas radiales dibujadas a 45° respecto a la vertical. En la Fig. 2.30 he tratado de indicar cómo se consigue esta aplicación. Vemos que la Fig. 2.29 muestra una importante propiedad de los diagramas conformes: la imagen es meramente un triángulo (rectángulo) finito, pese a que todo el espacio-tiempo infinito está englobado en el diagrama. Una propiedad característica de los diagramas conformes es que hacen posible que regiones infinitas del espacio-tiempo sean «comprimidas» de modo que quedan englobadas en una imagen finita. El propio infinito está también representado en el diagrama. Las dos líneas frontera inclinadas representan el infinito nulo pasado ⁻ y el infinito nulo futuro ⁺, donde cada geodésica nula (línea recta nula) en adquiere un punto extremo pasado en ⁻ y un punto extremo futuro en ⁺. (Es habitual pronunciar la letra como «scri» —que significa «script I».)^[2.44] Hay también tres puntos i⁻, i⁰ e i⁺ en la frontera que representan, respectivamente, el infinito de tipo tiempo pasado, el infinito de tipo espacio, y el infinito de tipo tiempo futuro; cada geodésica de tipo tiempo en adquiere el punto extremo pasado i⁻ y el punto extremo futuro i⁺, y cada geodésica de tipo espacio se cierra en un lazo vía el punto i⁰. (Pronto veremos por qué i⁰ debe ser considerado como un único punto).

Fig. 2.29. Diagrama conforme estricto del espacio de Minkowski .

Fig. 2.30. Para obtener la imagen normal de , imaginamos las fronteras (cónicas) inclinadas desplazadas hacia el infinito.

En esta coyuntura puede ser útil recordar el grabado de Escher en la Fig. 2.3(c) que proporciona una imagen conforme del plano hiperbólico entero. El círculo que lo limita representa su infinito, de un modo conformemente finito, de una manera esencialmente similar a la manera en que ⁺, ⁻, i⁻, i⁰ e i⁺ juntos representan el infinito para . De hecho, igual que podemos extender el plano hiperbólico, como una variedad conforme suave, más allá de su frontera conforme al plano euclidiano dentro del que está representado (Fig. 2.31), también podemos extender , suavemente, más allá de su frontera a una variedad conforme más grande. De hecho, es conformemente idéntico a una porción del modelo del espacio-tiempo conocido como universo de Einstein ε (o el «cilindro de Einstein»). Éste es un modelo cosmológico que es espacialmente una 3-esfera (S³) y completamente estático. La Fig. 2.32(a) da una imagen intuitiva de este modelo (el que Einstein obtuvo con la introducción original, en 1917, de su constante cosmológica Λ; véase §2.1), y la Fig. 2.32(b) proporciona un diagrama conforme estricto que lo representa. Nótese que en este diagrama hay dos «ejes de rotación» independientes, representados por las dos líneas de trazos verticales. Esto es del todo consistente; simplemente consideramos que el radio de la S², que representa cada punto en el interior del diagrama, se contrae hasta cero cuando nos acercamos a la línea de trazos. Esto sirve también para explicar el hecho bastante curioso de que el infinito espacial para es conformemente sólo el punto único i⁰, pues el radio de la S² que parecería haber representado se ha contraído hasta cero. Las secciones transversales espaciales S³ del espacio-tiempo ε surgen de este procedimiento. La Fig. 2.33(a) muestra cómo aparece como una subregión conforme de ε, y de hecho cómo podemos considerar la variedad entera ε formada, conformemente, por una sucesión infinita de espacios , donde el ⁺ de cada uno de ellos se ha unido al ⁻ del siguiente, y la Fig. 2.33(b) muestra cómo se hace esto en términos de diagramas conformes estrictos. Valdrá la pena tener esta imagen en mente cuando lleguemos a considerar el modelo propuesto en la Parte 3.

Fig. 2.31. Extendiendo el plano hiperbólico, como una variedad conforme suave, más allá de su frontera conforme al plano euclidiano dentro del que está representado.

Fig. 2.32. (a) Imagen intuitiva del universo de Einstein ε («cilindro de Einstein»); (b), (c) diagramas conformes estrictos del mismo objeto.

Fig. 2.33. Para ver por qué i⁰ es un único punto. (a) aparece como una subregión conforme de ε. La variedad entera ε puede considerarse formada, conformemente, de una infinita sucesión de espacios ; (b) muestra cómo se hace esto en términos de diagramas conformes estrictos.

Consideremos ahora las cosmologías de Friedmann introducidas en §2.1. Los diferentes casos K > 0, K = 0, K < 0, para Λ = 0, se ilustran en la Fig. 2.34(a), (b), (c), respectivamente. Las singularidades se representan aquí como líneas onduladas. Aquí he introducido una notación en la que un punto blanco «°» en la frontera representa toda una superficie esférica S², mientras que los puntos negros «•» (que ya teníamos en el caso de ) representan puntos únicos. Estos puntos blancos representan realmente las esferas frontera del espacio hiperbólico, en la representación conforme que utilizaba Escher en el caso 2-dimensional. Los casos correspondientes para constante cosmológica positiva (Λ > 0, donde en el caso K > 0 suponemos que la curvatura espacial no es suficientemente grande para superar a Λ y producir un recolapso final) se ilustran en la Fig. 2.35(a),(b),(c). Puede señalarse una propiedad importante de estos diagramas. El infinito futuro ⁺ de todos estos modelos es de tipo espacio, como se indica en el hecho de que la línea frontera final está siempre a menos de 45° de la horizontal, en contraste con el infinito futuro que ocurre cuando Λ = 0 (en los casos ilustrados en la Fig. 2.34(a), (b), (c) y la Fig. 2.29), donde la frontera está a 45°, de modo que ⁺ es entonces una hipersuperficie nula. Ésta es una propiedad general de la relación entre la naturaleza geométrica de ⁺ y el valor de la constante cosmológica Λ, y tendrá una importancia clave para nosotros en la Parte 3.

Fig. 2.34. Diagramas conformes estrictos para los tres casos diferentes, K > 0, K = 0, K < 0 para Λ = 0, de las cosmologías de Friedmann.

Todos estos modelos de Friedmann con Λ > 0 tienen un comportamiento en su futuro remoto (es decir, cerca de ⁺) que se aproxima mucho al espacio-tiempo de De Sitter , un universo modelo que está completamente vacío de materia y es extremadamente simétrico (siendo un equivalente minkowskiano a una esfera 4-dimensional). En la Fig. 2.36(a) he esbozado una versión 2-dimensional de , con sólo una dimensión espacial representada (donde el 4-espacio de De Sitter completo sería una hipersuperficie en un 5-espacio de Minkowski), y he dado un diagrama conforme estricto para el mismo en la Fig. 2.36(b). El modelo de estado estacionario, mencionado en §2.2, es sólo una mitad de , como se muestra en la Fig. 2.36(b). Debido al «corte» a través de que se requiere (frontera quebrada), el modelo de estado estacionario es en realidad lo que se denomina «incompleto», en direcciones pasadas. Hay geodésicas de tipo tiempo ordinarias —que podrían representar movimientos libres de partículas masivas— cuyas medidas temporales no se extienden a valores anteriores a cierto valor finito. Esto podría haberse considerado un fallo preocupante en el modelo si se hubiera aplicado a direcciones futuras, puesto que podría aplicarse al futuro de una partícula o un viajero espacial,^[2.45] pero aquí podemos decir simplemente que tales movimientos de partículas nunca se presentan.

Fig. 2.35. Diagramas conformes estrictos para modelos de Friedmann con Λ > 0. (a) K > 0; (b) K = 0; (c) K < 0.

Fig. 2.36. Espacio-tiempo de De Sitter: (a) representado (con 2 dimensiones espaciales suprimidas) en el 3-espacio de Minkowski; (b) su diagrama conforme estricto; (c) cortado por la mitad, obtenemos un diagrama conforme estricto para el modelo de estado estacionario.

Cualquiera que sea la idea que se pudiera asumir sobre la física de la materia, he indicado este tipo de incompletitud por una línea ligeramente irregular en el diagrama conforme estricto. El tipo restante de línea que estoy utilizando en mis diagramas conformes estrictos es una línea de puntos interna, para indicar el horizonte de sucesos de un agujero negro. En mis diagramas conformes estrictos utilizo consistentemente estos cinco tipos de líneas (de trazos para ejes de simetría, gruesas para el infinito, onduladas para una singularidad, ligeramente quebradas para incompletitud, y de puntos para un horizonte de agujero negro) y dos tipos de puntos (negros que representan un único punto en el 4-espacio, blancos que describen un S²), como se da en la clave en la Fig. 2.37.

Un diagrama conforme estricto pata el colapso de Oppenheimer-Snyder hacia un agujero negro se da en la Fig. 2.38(a). Este resulta al «pegar» una porción de un modelo de Friedmann en colapso y una porción de la extensión de Eddington-Finkelstein de la solución original de Schwarzschild, como se muestra en los diagramas conformes estrictos de la Fig. 2.38(b), (c); véase también la Fig. 2.39. Schwarzschild encontró su solución de las ecuaciones de Einstein en 1916, poco después de que este publicara las ecuaciones de su teoría de la relatividad general. Esta solución describe el campo gravitatorio externo de un cuerpo esféricamente simétrico y estático (tal como una estrella), y puede extenderse hacia dentro, como un espacio-tiempo estático, hasta su radio de Schwarzschild

donde M es la masa del cuerpo y G es la constante gravitatoria de Newton. Para la Tierra este radio sería de unos 9 mm, para el Sol sería de unos 3 km, pero en estos casos el radio estaría dentro del cuerpo y no habría distancias teóricas de relevancia inmediata para la geometría del espacio-tiempo, pues esta métrica de Schwarzschild sólo es válida para la región externa. Véase el diagrama conforme estricto en la Fig. 2.39(a).

Fig. 2.37. Clave para diagramas conformes estrictos.

Fig. 2.38. El modelo de Oppenheimer-Snyder de colapso a un agujero negro: (a) diagrama conforme estricto construido pegando; (b) parte izquierda de un modelo de Friedmann invertido en el tiempo (Fig. 2.34(b)), y (c) parte derecha del modelo de Eddington-Finkelstein (Fig. 239(b)). (En modelos locales, tales como éstos, se ignora Λ, de modo que se considera nulo).

Sin embargo, en el caso de un agujero negro el radio de Schwarzschild estaría en el horizonte. En este radio, la forma de Schwarzschild de la métrica se hace singular, por lo que originalmente se pensó que el radio de Schwarzschild era una singularidad real en el espacio-tiempo. Sin embargo, Georges Lemaître encontró, en 1927, que si abandonamos el requisito de que el espacio-tiempo permanezca estático, es posible extenderlo de una manera perfectamente suave. Una descripción más simple de esta extensión fue hallada por Arthur Eddington en 1930 (aunque él omitió señalar lo que se había conseguido), descripción que fue redescubierta, y sus implicaciones claramente enunciadas, por David Finkelstein en 1958; véase el diagrama conforme estricto de esto en la Fig. 2.39(b). Lo que se conoce como la «extensión maximal de la solución de Schwarzschild» (a veces llamada extensión de Kruskal-Szekeres, aunque una descripción equivalente pero más complicada fue encontrada mucho antes por J. L. Synge)^[2.46] se da en el diagrama conforme estricto de la Fig. 2.39(c).

Fig. 2.39. Diagramas conformes estrictos de un vacío (Λ = 0) esféricamente simétrico: (a) solución original de Schwarzschild, externa al radio de Schwarzschild; (b) extensión a la métrica de colapso de Eddington-Finkelstein, y (c) extensión completa a la forma de Kruskal/Synge/Szekeres/Fronsdal.

En §3.4 llegaremos a otra propiedad de los agujeros negros que, aunque actualmente tiene un efecto extremadamente minúsculo, tendrá en definitiva una importancia crucial para nosotros. Mientras que según la física clásica de la relatividad general de Einstein un agujero negro debería ser completamente negro, un análisis realizado por Stephen Hawking en 1974^[2.47] mostró que cuando se introducen en la imagen los efectos de la teoría cuántica de campos en fondos espaciotemporales curvos, un agujero negro debería tener una temperatura pequeñísima T, que es inversamente proporcional a la masa del agujero negro. Para un agujero negro de 10Mʘ, por ejemplo, esta temperatura sería extraordinariamente minúscula, unos 6 × 10⁻⁹ K, que es del mismo orden que la temperatura más baja obtenida en un laboratorio (al menos hasta 2006). Ésta es aproximadamente la temperatura que podrían tener los agujeros negros que puedan existir hoy. Los agujeros negros más grandes serían aún más fríos, y la temperatura del agujero negro de unas ~ 4.000.000 Mʘ en el centro de nuestra galaxia sería de unos 1,5 × 10⁻¹⁴ K. Si consideramos que la temperatura ambiente de nuestro universo en el momento actual es la del CMB, encontramos que ésta tiene el valor inmensamente más caliente de ~ 2,7 K.

Pese a todo, si adoptamos una visión a muy, muy largo lazo, y tenemos en mente que la expansión exponencial de nuestro universo, si continúa indefinidamente, llevará a un enorme enfriamiento del CMB, cabría esperar que su temperatura se reduzca incluso hasta la temperatura de los agujeros negros más grandes que hayan existido nunca. Después de eso, el agujero negro empezará a irradiar su energía al espacio circundante, y al perder energía debe perder también masa (por la E = mc² de Einstein). A medida que pierda masa, se hará más caliente, y poco a poco, al cabo de un período de tiempo increíble (quizá de hasta 10¹⁰⁰ —es decir, un «gugol»— de años, en el caso de los mayores agujeros negros actuales), se contraerá por completo hasta desaparecer finalmente con un «pop», pues esta explosión final difícilmente merece el nombre de «bang», ya que probablemente tendría sólo la energía de una pequeña granada de artillería ¡lo que tiene algo de anticlímax después de tan larga espera!

Por supuesto, esto supone una enorme extrapolación de nuestro conocimiento físico actual. Pero el análisis de Hawking está en buen acuerdo con principios generales aceptados, y parece que estos principios no nos dejan escapar de esta conclusión global. Por consiguiente, la estoy aceptando como una explicación plausible del destino final de un agujero negro. De hecho, esta expectativa será un ingrediente importante en el esquema que presentaré en la Parte 3 de este libro. En cualquier caso, es relevante presentar un esbozo de este proceso en la Fig. 2.40, junto con su diagrama conforme estricto, en la Fig. 2.41.

Por supuesto, muchos espacio-tiempos no poseen simetría esférica, y una descripción en términos de un diagrama conforme estricto no puede dar siquiera una aproximación razonable. Sin embargo, la noción de un diagrama conforme esquemático puede ser con frecuencia de gran valor para clarificar ideas. Los diagramas conformes esquemáticos no tienen las reglas precisas que gobiernan los diagramas estrictos, y a veces es necesario imaginar que el diagrama se presenta en 3 (o incluso 4) dimensiones para que sus implicaciones sean plenamente apreciadas. La idea básica consiste en hacer uso de dos de los ingredientes de las representaciones conformes de los espacio-tiempos que hacen finitas las magnitudes infinitas. Éstos son, por una parte, la introducción en nuestra comprensión finita de las regiones infinitas del espacio y el tiempo que hemos visto en nuestros diagramas conformes estrictos, que se han mostrado por fronteras de líneas gruesas; y por otra, el despliegue de las regiones que son infinitas en un sentido diferente, a saber, las singularidades espaciotemporales que en nuestros diagramas estrictos se denotaban por fronteras de líneas onduladas. Lo primero se ha conseguido por un factor conforme (el Ω de g → Ω²g en §2.3) al que se ha permitido tender suavemente a cero, de modo que las regiones infinitas se «comprimen» a algo finito. Lo segundo se ha conseguido por un factor conforme al que se ha permitido hacerse infinito, de modo que las regiones singulares se han hecho finitas y suaves al «estirar» las regiones singulares. Por supuesto, no se nos garantiza que tales procedimientos funcionarán realmente en cualquier caso concreto. Sin embargo, encontraremos que ambos procedimientos desempeñan papeles importantes en las ideas a las que llegaremos, y la combinación de los dos será fundamental para lo que propondré en la Parte 3.

Fig. 2.40. Agujero negro en evaporación de Hawking.

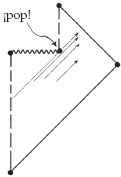
Fig. 2.41. Diagrama conforme estricto del agujero negro en evaporación de Hawking.

Para terminar esta sección, será útil presentar un contexto en el que estos dos procedimientos pueden ser particularmente ilustrativos, y es la cuestión de los horizontes cosmológicos. De hecho, hay dos nociones distintas que, en el contexto cosmológico, se conocen como «horizontes».^[2.48] Una de ellas es la que se conoce como horizonte de sucesos; la otra es un horizonte de partículas.

Consideremos primero la noción de un horizonte de sucesos cosmológico. Está íntimamente relacionada con la de horizonte de sucesos de un agujero negro, aunque la última tiene un carácter más «absoluto» en el sentido de que es menos dependiente de la perspectiva de un observador. Los horizontes de sucesos cosmológicos ocurren cuando el modelo posee un ⁺ que es de tipo espacio, como sucede con todos los modelos de Friedmann Λ > 0 que se muestran en los diagramas conformes estrictos de la Fig. 2.35 y en el modelo de De Sitter de la Fig. 2.36(b), pero la idea se aplica también en situaciones de un ⁺ de tipo espacio donde no se supone simetría (que es una propiedad general de Λ > 0). En los diagramas conformes esquemáticos de la Fig. 2.42(a),(b) he indicado (para 2 o 3 dimensiones espaciotemporales, respectivamente) la región del espacio-tiempo que es en principio observable para un observador O (¡considerado inmortal!) con línea de universo l que termina en un punto o⁺ en ⁺. Este horizonte de sucesos ⁻(o⁺) del observador es el cono de luz pasado de o⁺.^[2.49] Cualquier suceso que ocurre fuera de ⁻(o⁺) permanecerá inobservable para siempre para O. Véase la Fig. 2.43. Nótese, sin embargo, que la localización exacta del horizonte de sucesos depende mucho del punto terminal concreto o⁺.

Por el contrario, los horizontes de partículas aparecen cuando la frontera pasada —que normalmente se considera una singularidad y no el infinito— es de tipo espacio. De hecho, como puede apreciarse de los diagramas conformes estrictos mostrados aquí en los que aparecen singularidades, un carácter de tipo espacio es la norma para las singularidades espaciotemporales. Esto está íntimamente relacionado con la cuestión de la «censura cósmica fuerte» que abordaré en la próxima sección. Llamemos ⁻ a esta frontera singular inicial. Si el suceso o es la localización espaciotemporal de un observador O, entonces podemos considerar el cono de luz pasado ⁻(o) de o, y ver dónde corta a ⁻. Cualquier partícula que se origina en ⁻ fuera de esta intersección nunca entrará en la región visible para el observador en el suceso o, aunque si se permite que la línea de universo de O se extienda al futuro, entonces cada vez más partículas entrarán en su campo de visión. Es habitual considerar el horizonte de partículas real del suceso o como el lugar geométrico descrito por líneas de universo de galaxias idealizadas, que tienen origen en la intersección de ⁻(o) con ⁻. Véase la Fig. 2.44.

Fig. 2.42. Diagramas conformes esquemáticos de horizontes de sucesos cosmológicos que ocurren cuando K > 1: (a) 2-dimensional; (b) 3-dimensional.

Fig. 2.43. El horizonte de sucesos del observador inmortal O representa una frontera absoluta para los sucesos que son siempre observables para O; este horizonte depende de la elección de la historia de O. Un cambio de opinión en X puede dar como resultado un horizonte de sucesos diferente.

Fig. 2.44. Diagramas conformes esquemáticos de horizontes de partículas en (a) 2 dimensiones, (b) 3 dimensiones.