11 

Universos marginales

Teorías, teorías, miles y miles de ellas, lanzadas sobre mí como hojas barridas por el viento, como el contenido de una colosal fábrica de papel a merced de la tormenta, como nubes de polvo ante el avance huracanado de la mente. Jadeando en este vasto torbellino de aridez, casi olvidé que cada mota de él contenía algunas esporas de verdad orgánica, generalmente agostadas y muertas pero algunas veces vivas, henchidas, significativas.

Olaf Stapledon^[385]

Universos envueltos sobre sí mismos

Reading es un lugar curioso. Incluso sus más férreos defensores tienden a hablar de él en relación con su proximidad a otros lugares. «Solo está a 25 minutos en tren del centro de Londres», decía con entusiasmo el jefe de turno. «¡La lanzadera a Heathrow solo tarda 45 minutos!», decía la camarera de la cafetería del centro comercial.

Revista de British Airways^[386]

Si los universos pueden aparecer «de la nada» sin violar las leyes de la física, quizá la creación del universo pueda describirse utilizando esas mismas reglas. Tradicionalmente, los cosmólogos que creían que el universo tenía un principio se habían sentido satisfechos con considerarlo como un lugar y tiempo en el que las leyes fallaban. Esas leyes empezaron a existir al mismo tiempo que el espacio, el tiempo y el universo físico. Toda nuestra charla sobre «otros» universos y sobre el multiverso cuestiona este punto de vista. Cada vez más, vemos nuestro universo como un resultado de las leyes de la Naturaleza, quizá uno entre muchos en un multiverso: un pequeño acontecimiento local en una historia eterna. Aunque esto degrada el estatus del inmenso universo que vemos a nuestro alrededor, eleva el de las leyes de la Naturaleza. Al parecer son capaces de controlar e intervenir en más universos, aparte del que nosotros podemos observar. Durante todo el siglo XX, los cosmólogos se acostumbraron a la idea de estudiar los distintos tipos de universo que surgían de las ecuaciones de Einstein, pero esperaban que algún principio o estado inicial especial seleccionase aquel que mejor describía el universo real. Ahora, inesperadamente, nos encontramos con que puede haber sitio para muchos de estos universos posibles, quizá todos ellos, en algún lugar del multiverso.

¿Qué clase de universo sería más probable que se crease de la nada? Todos los universos que obedecen las ecuaciones de Einstein parecen tener cero energía y cero carga eléctrica. Esas son dos de las tres magnitudes más importantes que se conservan en todos los procesos físicos. La energía y el cambio pueden trasladarse y redistribuirse, pero al totalizar cada uno de ellos, teniendo en cuenta positivos y negativos, la suma total siempre debe ser la misma. Las cosas son algo distintas en lo que respecta a la tercera magnitud importante que se conserva, el momento angular. Se trata de una medida de la rotación, y ya hemos visto que las ecuaciones de Einstein no exigen que sea cero del mismo modo que con la energía y la carga eléctrica. Gödel halló que podía haber universos en rotación, pero aún no hemos hallado pruebas de una rotación global del universo. Ni tampoco esperamos hacerlo porque, en caso de inflación, esta reduciría cualquier rotación preexistente a niveles imposibles de observar^[387].

En 1973, el físico de partículas norteamericano Edward Tryon^[388] intentó efectuar una especulación de este tipo (sobre la que Pascual Jordan y George Gamow habían reflexionado antes^[389]). Sugirió que todo el universo podía ser una fluctuación virtual del vacío cuántico, gobernado por el Principio de incertidumbre de Heisenberg, que limita nuestro conocimiento simultáneo de la posición y del momento, o del instante temporal y la energía, de cualquier objeto de la Naturaleza. Dentro de esta imagen pensó que el universo podía ser «simplemente una de esas cosas que suceden de vez en cuando». La forma energía-tiempo del principio de incertidumbre exige que el producto de la duración de una fluctuación y de su energía sea mayor que la constante cuántica de Planck (Δt × ΔE > h)^[390]. Esto sugiere que una fluctuación de energía cero (como nuestro universo) podría tener una duración infinita. De hecho, la duración más probable es de 10⁻⁴³ segundos. Es necesario que la inflación actúe en estas minúsculas y fugaces fluctuaciones para que se hagan astronómicamente grandes y viejas. Tryon no podía explicar por qué nuestro universo había vivido tanto tiempo, y aún faltaban ocho años para que se descubriera la inflación. Lo único que podía sugerir para conciliar esta imagen con la rareza de las fluctuaciones del vacío de gran tamaño y larga vida era una simple explicación antrópica para la excepcional fluctuación, porque es una condición necesaria para los observadores:

La lógica de la situación, sin embargo, dicta que los observadores siempre se hallarán en universos capaces de generar vida, y dichos universos son imponentemente grandes. No podríamos haber visto este universo si su tiempo de expansión-contracción hubiese sido menor de los 10¹⁰ años que el Homo sapiens necesita para evolucionar.

Si se pudiese hacer que funcionara una versión más sofisticada de esta idea, deberíamos pensar acerca de las propiedades más probables de un universo creado. Supongamos que se tratase de un universo finito. Hay muchos universos finitos, con todos los tamaños posibles, y hemos visto por qué deberíamos residir en uno grande, aunque podría haber empezado muy pequeño y sufrido inflación. La otra pregunta que debemos hacernos sobre cualquier universo que apareciese así es: ¿cuál sería su topología?

Hemos visto que las ecuaciones de Einstein generan universos con espacios que pueden ser curvados o planos. La distribución de materia dentro del universo dicta la forma local del espacio. Pero esta información no da todos los datos sobre la forma general del espacio. Las ecuaciones de Einstein dejan indeterminada una propiedad global, cuya forma se debe suponer simple (o incluso complicada). Esa propiedad se denomina la «topología» del universo, y su importancia la reconoció inmediatamente Alexander Friedmann en 1922, cuando descubrió los primeros universos en expansión con espacios positiva y negativamente curvados.

La topología es distinta de la geometría. En el capítulo 2 nos tropezamos con la idea de geometrías no euclídeas en superficies curvadas. Vamos a llevar este concepto un poco más allá. Para hallar la curvatura en una superficie curvada marcamos tres puntos distintos, A, B y C, y los unimos —A con B, B con C, C con A— por los caminos más cortos posibles sobre la superficie. En una superficie plana, esta operación crea un triángulo cuyos ángulos interiores suman 180 grados. Hazlo sobre una hoja de papel. Enrolle luego el papel en forma de cilindro con el triángulo en el exterior. Si se examina el triángulo sobre el cilindro se verá que sus lados siguen siendo líneas rectas y que sus tres ángulos interiores siguen sumando 180 grados.

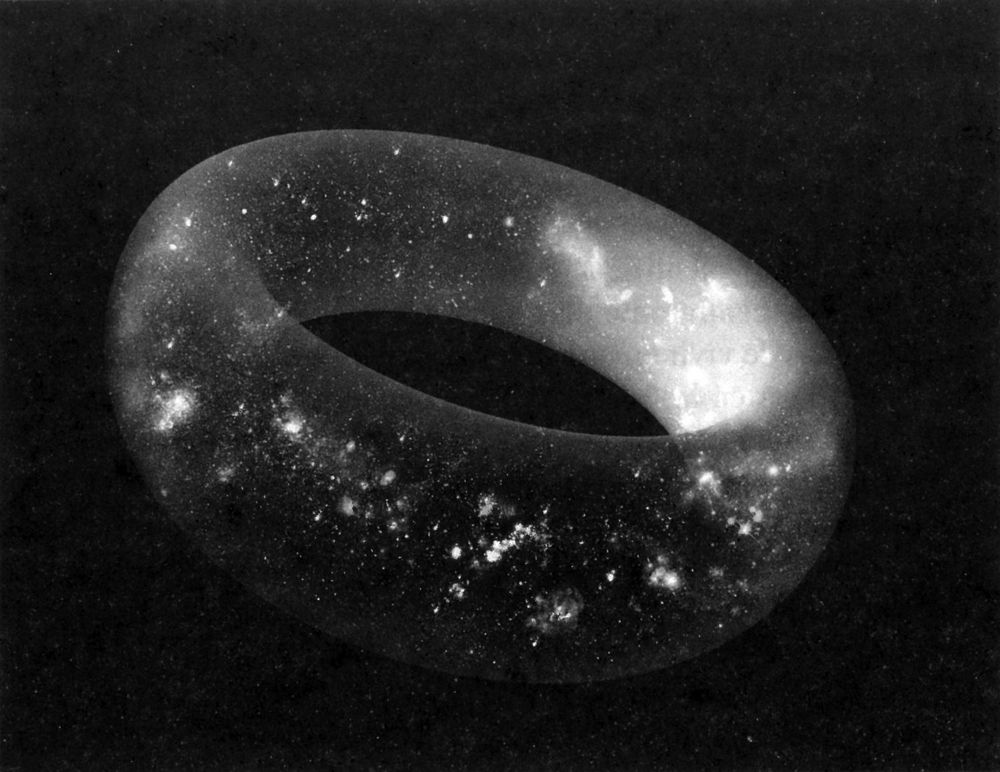
FIGURA 11.1. Un universo bidimensional de espacio con la topología de la superficie de una rosquilla.

El cilindro no es una superficie geométrica curvada, lo cual es bastante sorprendente. Lo que lo distingue de la hoja plana es su topología general. El efecto de cambiar la topología de esta forma puede ser espectacular. En el caso del universo, podría tener una geometría euclídea plana que se extendiese sin límites en todas direcciones: su volumen sería infinito. Pero si cada una de las tres direcciones se enrolla como un cilindro para construir una rosquilla tridimensional, el espacio será plano en todas partes pero el volumen de espacio será ahora finito (Figura 11.1). Por esto es por lo que Friedmann se cuidó mucho de decir que los universos con geometría plana o de curvatura negativa eran infinitos mientras que los de curvatura positiva eran finitos en volumen. Puso el ejemplo del cilindro para mostrar que bastaba con enrollar el espacio en cada dirección para crear un universo de volumen finito aunque el espacio sea plano o con curvatura negativa. Friedmann estaba familiarizado con este tipo de sutilezas matemáticas, pero la mayoría de astrónomos de su época se la hubiesen perdido. Aunque la teoría de Einstein tiene la hermosa propiedad de que la distribución de materia y energía en el universo determina la geometría de su espacio y el ritmo de paso del tiempo localmente en todas partes, no fija la topología del espacio^[391].

Si nuestro universo tuviera una de esas topologías «enrolladas», y hay muchas otras variedades aparte de la rosquilla simple, las medidas de la curvatura y del ritmo de expansión podrían hacer que pareciese «abierto», infinito y en eterna expansión, cuando en realidad sería finito. Esta posibilidad fue examinada por diversos cosmólogos en la década de 1970. En 1971, George Ellis, de la Universidad de Cambridge, investigó el catálogo de posibles topologías^[392] que el universo podía poseer y halló que algunas de ellas crearían extraños conflictos con algunos aspectos de la física —por ejemplo, en algunas, en las que se retorcía el espacio antes de «pegar» juntos los lados opuestos, una partícula elemental «diestra» podría efectuar un viaje y regresar como partícula «zurda», pero muchas otras evitaban este tipo de problemas^[393].

En 1974, dos científicos soviéticos, Dimitri Sokolov y Víctor Shvartsman, se centraron en las consecuencias observacionales para los astrónomos de vivir en uno de estos universos «enrollados»^[394]. Empezaron a pensar en las consecuencias del enrollado en las imágenes de galaxias brillantes (Figura 11.2). Es como si viviésemos en la galería de los espejos. En cada dirección vemos múltiples imágenes que parecen hacerse cada vez más tenues porque la luz ha recorrido cada vez más circuitos del universo finito antes de llegar a nosotros. Si uno está en una sala con espejos en las paredes se pueden ver innumerables imágenes reflejadas de uno mismo en todas las direcciones, cada una más pequeña que la anterior hasta perderse en la distancia.

La forma más simple de comprobar si estamos en un universo enrollado es elegir un cúmulo brillante de galaxias —uno de los preferidos es el Cúmulo de Coma, que contiene más de 1000 galaxias y se encuentra a 321 millones de años luz de distancia— y buscar copias en el cielo. No serán copias idénticas, porque las imágenes representarán el cúmulo en diversos momentos de su vida, y la luz habrá seguido trayectorias distintas hasta llegar a nosotros. De todos modos, si hay reflejo, la primera copia debería ser evidente.

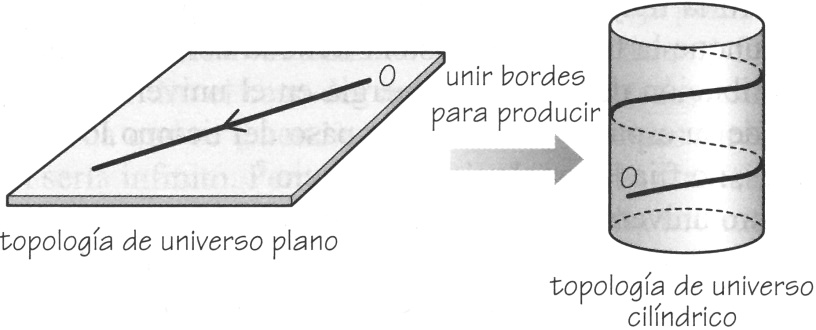
FIGURA 11.2. Una topología cilíndrica creada enrollando un plano. Un observador situado en el universo cilíndrico recibe fotones que han viajado durante mucho tiempo sin venir de tan lejos como en el universo plano, y han circunnavegado el espacio muchas veces.

Con estas consideraciones se pudo establecer un límite inferior al tamaño del universo, si es que utilizaba una topología enrollada para crear la ilusión de ser infinitamente grande. El análisis de Sokolov y Shvartsman, y un posterior segundo examen por parte de Richard Gott en 1980^[395], halló un límite inferior de entre 400 y 600 millones de pársecs^[396] para el tamaño de todo el universo. En aquel momento aún no se había descubierto el universo inflacionario, y el punto de vista predominante era que había un único «universo» que podía ser finito o infinito.

En 1984, en Moscú, Yakob Zeldovich y Andrei Starobinsky volvieron a la cuestión de la creación de universos de la «nada» —o, al menos, del vacío cuántico— si tenían diferentes topologías enrolladas posibles^[397]. En aquel momento se pensaba que solo podían crearse de esa forma universos finitos^[398], así que era interesante descubrir si las topologías peculiares eran más probables que la estándar. Hallaron que un universo plano simple con una topología enrollada podía aparecer como fluctuación cuántica mientras las distancias de enrollado en las tres direcciones fuesen aproximadamente las mismas. Si eran de un tamaño muy distinto en cada dirección, el universo debía surgir de una singularidad de densidad infinita.

Únicamente a partir de las ecuaciones de Einstein no hay forma de decidir cuál debería ser la topología del universo. Tradicionalmente, los cosmólogos han adoptado las topologías más simples posibles, pero se podría apuntar que las topologías exóticas enrolladas son mucho más numerosas que las simples, así que los universos enrollados podrían ser más probables si estuviésemos sacando universos de una chistera de forma aleatoria. Otros sostienen que los universos finitos son más naturales y esquivan las consecuencias alarmantes, como las paradojas de replicación, además de permitir que la teoría cuántica funcione de forma más natural. Eso significa que se deben tener en cuenta todos los universos finitos, no solo lo más simples, de topología esférica, que Friedmann examinó por primera vez. Los opuestos a los universos enrollados son escépticos. ¿Por qué debería estar la escala de identificación del espacio en un intervalo interesante? Parece una coincidencia extraordinaria que solo fuese observable hoy. Esta es una buena objeción en el caso de que el universo tenga curvatura cero y el espacio sea exactamente euclídeo. No hay entonces motivo que explique por qué la escala de enrollado debe estar en las proximidades de la escala de nuestro horizonte visible. Podría ser cualquiera. Sin embargo, si el universo tiene curvatura negativa, su radio de curvatura es muy próximo al tamaño del universo visible, y la escala de enrollado podría estar estrechamente relacionada con él, lo cual no sería en absoluto una coincidencia.

Esta cuestión topológica ha resucitado en los últimos años a raíz de que los astrónomos están intentando dar explicación a cada uno de los detalles de la radiación de fondo de microondas. Al principio parecía haber un ligero déficit en las variaciones de temperatura en separaciones de unos 10 grados de arco en el cielo. Esto se podía explicar en un universo enrollado porque las grandes ondas de variación de temperatura no se adaptan con facilidad a un universo finito «pequeño», y las fluctuaciones de temperatura disminuirían en las proximidades de la escala de enrollado^[399]. Sin embargo, recientemente ha habido pruebas de que estos déficits identificados podrían ser estadísticamente no significativos. Sin duda se hablará más de esto en los próximos años, cuando el satélite Planck empiece a enviar datos sobre su exploración del cielo en 2011.

Universos cuánticos

El número que ha marcado es imaginario. Gire su teléfono noventa grados y vuelva a marcar.

Mensaje de contestador «imaginario»

Uno de los mayores desafíos de la física moderna ha sido la unión de la teoría de la gravedad de Einstein y la teoría cuántica de la materia y la luz. Tradicionalmente, la teoría cuántica domina el mundo de pequeña escala de los átomos y sus componentes, donde la gravedad es tan débil que no se percibe. La gravitación gobierna las estructuras más grandes del universo actual. Pero, si retrocedemos en el tiempo hacia el aparente inicio de la expansión del universo, nos encontramos con un momento en que sabemos que la gravedad y la teoría cuántica deben combinarse para formar un nuevo entorno en el que las incertidumbres de la realidad cuántica invaden el propio tejido del espacio y el tiempo. Parece sorprendente, pero las constantes de la Naturaleza definen con total precisión el momento en que esto debe suceder.

La lección que podemos aprender de la teoría cuántica es que todas las partículas tienen un aspecto cuántico ondulatorio. Las longitudes de onda de sus efectos cuánticos son inversamente proporcionales a sus masas. Cuando la longitud de onda cuántica supera el tamaño físico de una partícula, se comporta de un modo ondulatorio intrínsecamente cuántico. En la situación contraria, como es el caso de las personas como nosotros mismos cuando andamos por la calle, el aspecto ondulatorio cuántico es insignificante. Si seguimos la masa de la parte del universo contenida dentro de una esfera cuyo radio es la velocidad de la luz multiplicada por la edad del universo, podemos preguntarnos cuándo la longitud de onda cuántica de esa masa supera el diámetro de la bola. En esa situación, toda la región del universo con conexión causal se comportará como una onda cuántica, y se espera que las ecuaciones del universo de Einstein no funcionen. Este tiempo crucial, que es muy reducido, es igual a t_Q = 10⁻⁴³ segundos. En ese tiempo, las señales lumínicas solo habrían podido recorrer alrededor de 10⁻³³ centímetros.

Este mínimo latido de tiempo es realmente fundamental. Es la unidad de tiempo natural que definen las leyes de la física, sin sesgo antropomórfico alguno. Lo definen las constantes de la Naturaleza únicamente a partir de las cualidades cuánticas, relativistas y gravitatorias del universo^[400]. Si parece tan pequeño es porque lo medimos en unidades «humanas» —segundos—, que caracterizan instantes discernibles de nuestra experiencia. Decimos que el universo tiene una edad de 14 000 millones de años, lo que equivale a unos 10⁶⁰ de estos latidos cuánticos. En este sentido, el universo es muy viejo. Un universo joven tendría una edad de solo unos pocos de estos latidos cuánticos.

Decimos que, cuando el universo tiene una edad de un latido, el tamaño de la esfera que las señales de luz han podido recorrer es de unos 10⁻³³ centímetros. Parece un tamaño inimaginablemente pequeño, pero hay una buena forma de hacerse una idea. Tomemos una hoja de papel A4 e imaginemos que la partimos por la mitad, una y otra vez. Después de repetir el proceso solo 30 veces, el tamaño de la hoja será el de un átomo individual. Si se repite 47 veces, el tamaño será el de un protón. Con 114 veces, la hoja medirá alrededor de 10⁻³³ centímetros de ancho. Bastan 114 mitades para llevarnos de una hoja de papel A4 a la longitud más pequeña a la que el concepto de distancia aún tiene sentido físico. En la otra dirección, basta con duplicar el tamaño de la hoja de papel 90 veces para alcanzar la escala de todo el universo observable actualmente, unos 14 000 millones de años luz. Así que, en realidad, estas distancias inimaginables, tanto por grandes como por pequeñas, no son tan fieras como las pintan.

Observamos que no se espera que la inflación del universo dé comienzo hasta que no hayan pasado alrededor de 100 millones de latidos cuánticos, en t = 10⁻³⁵ segundos, con lo que los problemas de la gravedad cuántica no afectan a esos eventos. Sin embargo, si queremos investigar cómo era el universo antes del inicio de la inflación y preguntarnos si tuvo un principio en el tiempo, tenemos que enfrentarnos al problema de la gravedad cuántica.

Hemos visto que los viejos estudios matemáticos de las ecuaciones de Einstein de los que fueron pioneros Roger Penrose y Stephen Hawking, a mediados de la década de 1960, indicaban con todo detalle las condiciones exactas bajo las que el universo experimentó un principio en el pasado. Por desgracia, las hipótesis a partir de las que se llega a esta conclusión ya no son válidas cuando extrapolamos a la época de la gravedad cuántica. Las ecuaciones de Einstein deberán modificarse, y puede que la gravedad ya no sea atractiva. Eso no significa que no hubiese un principio si hubo inflación, pero ya no podemos deducir que ese principio debía haber existido. Nuestros teoremas ya no pueden salir en nuestra ayuda. De hecho, el tipo de materia necesaria para que tenga lugar la inflación y, como veremos en el próximo capítulo, para explicar la expansión del universo que observamos actualmente debe violar las hipótesis necesarias para demostrar que hubo un principio en el tiempo.

También hemos visto que el universo inflacionario eterno introduce una perspectiva completamente nueva en la cuestión del principio del universo en su conjunto. Cada región, como la que denominamos nuestro universo visible, tiene un principio en esta teoría, pero el proceso global de autorreproducción que produce incontables universos en inflación dentro del multiverso infinito no necesita tener un principio. Puede haber existido siempre, y existirá siempre en el futuro si creemos en las expectativas de esta teoría.

FIGURA 11.3. John A. Wheeler (1911-2008).

No hay una formulación consensuada para una cosmología cuántica. En muchos sentidos, la idea en sí es problemática, porque estamos acostumbrados a utilizar la mecánica cuántica para predecir lo que verá un observador cuando se efectúe una medida. Por ejemplo, la medida podría ser determinar el número de electrones que surgen de una desintegración radiactiva en un intervalo de energías determinado. Antes de efectuar la medida, todo consiste en una onda de diferentes posibilidades; después de la medida se registra un resultado definido. Lo único que podemos hacer es predecir la probabilidad de cualquier posible resultado medido. Sin embargo, cuando hablamos del universo, no hay observadores externos para efectuar medidas, y la filosofía entera de la mecánica cuántica se modifica. Debemos predecir correlaciones entre diferentes cosas. Por ejemplo, si observamos que el ritmo de expansión del universo adopta un determinado valor hoy, ¿cuál es la probabilidad de que midamos también que la agrupación de galaxias se extienda hasta una escala de distancia concreta? Sin embargo, en la práctica estamos muy lejos de poder deducir ninguna de esas probabilidades.

FIGURA 11.4. Bryce y Cecile DeWitt paseando en los Alpes franceses en 1963.

Muchos intentos de estudiar la mecánica cuántica de los universos emplean una ecuación especial hallada por John A. Wheeler y Bryce DeWitt en 1967, denominada «ecuación de Wheeler-DeWitt^[401]» (DeWitt siempre la describía como la ecuación de Einstein-Schrödinger y la atribuía a Wheeler, mientras que Wheeler insistía en llamarla ecuación de DeWitt. Finalmente, en 1988 llegaron al acuerdo de llamarla ecuación de Wheeler-DeWitt).

La ecuación de Wheeler-DeWitt hace un primer intento de combinar las ecuaciones de la relatividad general de Einstein con la ecuación de Schrödinger que describe cómo cambia la función de onda cuántica con el espacio y el tiempo. Sus soluciones dan una función de onda para el universo. Si esta ecuación pudiera resolverse nos diría la probabilidad de que un universo evolucionase de un estado a otro. Para encontrar soluciones así es necesario especificar unas condiciones iniciales para la función de onda del universo, y no es obvio cuáles deben ser. Se han llevado a cabo algunas exploraciones de este dilema, que ilustran algunas de las peculiares consecuencias de un universo cuántico.

El enfoque de James Hartle y Stephen Hawking era muy radical^[402]. Hawking había trazado la idea general en una charla en la Academia Pontificia del Vaticano en 1982^[403]. Parece que en este caso se producía una «resonancia» especial con el interés particular del Vaticano por el «principio» del universo, y Georges Lemaître, el arquitecto de la idea del universo del big bang, fue presidente de la Academia Pontificia entre 1960 y 1966. Hartle y Hawking utilizaron una elegante formulación de la mecánica cuántica introducida por Richard Feynman para calcular la probabilidad de que el universo se encontrase en un estado específico. Para calcular la probabilidad de que el universo evolucione del estado A al estado B se tienen en cuenta las contribuciones de todas las posibles trayectorias a través del espacio y el tiempo que la evolución pueda tomar para ir de A a B. En mecánica cuántica, el universo tiene una cierta probabilidad para tomar cualquiera de ellas, pero en la situación en la que el universo se hace cada vez más grande y más viejo y los efectos cuánticos son cada vez menos importantes, una de estas trayectorias es dominante y las otras se cancelan entre sí como pares de ondas en las que las crestas y los valles se superpusiesen. Esta evolución predominante se denomina «trayectoria clásica» y corresponde a lo que Einstein, o incluso Newton, habría predicho sin incluir la mecánica cuántica (Figura 11.5).

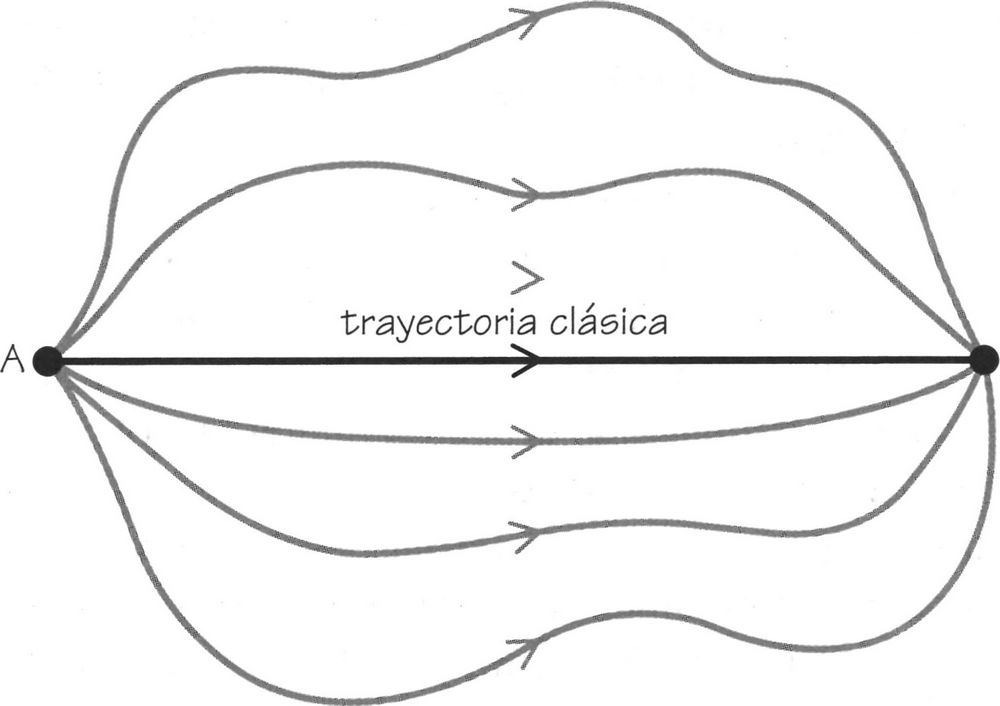
FIGURA 11.5. Trayectorias evolutivas entre dos estados del universo, A y B. Las leyes de Newton dictan que se sigue la «trayectoria clásica» única. La mecánica cuántica solo nos da la probabilidad de que haya una transición de A a B, que es una media ponderada sobre todas las posibles trayectorias entre A y B, algunas de las cuales se muestran aquí.

Generalmente, cuando se efectuaban estos cálculos, las posibles rutas para la evolución de A a B solo incluían las trayectorias a través del espacio y el tiempo, denominadas «de Lorentz». Se trata de las historias ordinarias que las partículas trazan si se mueven a la velocidad de la luz o más lento. Cuando vas al trabajo andando, o en bicicleta, sigues una trayectoria de Lorentz a través del espacio y el tiempo. Pero Hartle y Hawking querían incluir otro conjunto de trayectorias, denominadas «euclídeas», en las que el tiempo se convertía en una cuarta dimensión del espacio. Esto puede parecer extraño, pero los físicos habían utilizado el truco de convertir el tiempo en espacio cuando empezaron a efectuar estos cálculos porque los facilitaba en gran medida. Al final se trataba de cambiar de nuevo una de las dimensiones espaciales por tiempo. No era más que un método práctico, como utilizar coordenadas distintas para trazar un gráfico. Pero Hartle y Hawking no pretendían considerar esto únicamente como un método práctico para hacer los cálculos más sencillos: proponían un estado inicial en el que el tiempo se había convertido en otra dimensión del espacio.

Esto suena bastante raro, pero quizá podamos arreglárnoslas sin el tiempo. Toda la información que se necesita para etiquetar diferentes estados del universo y distinguir el futuro del pasado se puede obtener sin siquiera mencionar el «tiempo». Incluso actualmente percibimos algo similar. Si utilizásemos la temperatura de la radiación de fondo como reloj, la disminución de la temperatura se podría utilizar para distinguir el futuro del pasado. En el universo cuántico de Hartle y Hawking, la evolución del universo de un estado a otro está dominada por las trayectorias euclídeas cuando el universo es muy caliente y pequeño, pero son las de Lorentz las que dominan cuando es grande y frío.

Todo esto tiene dos consecuencias sorprendentes. El tiempo no es fundamental en esta teoría. Es una cualidad que surge cuando el universo se hace lo bastante grande como para que los característicos efectos cuánticos dejen de ser significativos: el tiempo es algo que solo aparece de forma concreta en el limitador entorno no cuántico. Si efectuamos el seguimiento del universo de Hartle-Hawking hacia atrás hasta tamaños muy pequeños, las trayectorias cuánticas euclídeas pasan a dominar. El concepto de tiempo desaparece y el universo se aproxima cada vez más a un espacio de cuatro dimensiones. No hay un principio temporal del universo, porque el tiempo desaparece.

Este enfoque se suele describir diciendo que el tiempo se hace «imaginario», porque la transformación que convierte el tiempo en otra dimensión espacial corresponde a multiplicarla por un número imaginario, la raíz cuadrada de menos uno. Si no eres matemático, esto puede sonar más bien exótico, pero tiene una explicación simple y muy geométrica: corresponde a girar el eje temporal de nuestro gráfico 90 grados, de forma que se convierta en un eje espacial. Si miramos nuestro diagrama simple espacio-tiempo con los rayos de luz viniendo hacia nosotros en líneas rectas desde el pasado podremos ver el efecto que tendrá en el pasado el paso al tiempo imaginario. El eje vertical del tiempo gira para hacerse horizontal como el espacio, y el pasado se convierte en una superficie suave redondeada como el fondo de una botella (Figura 11.6).

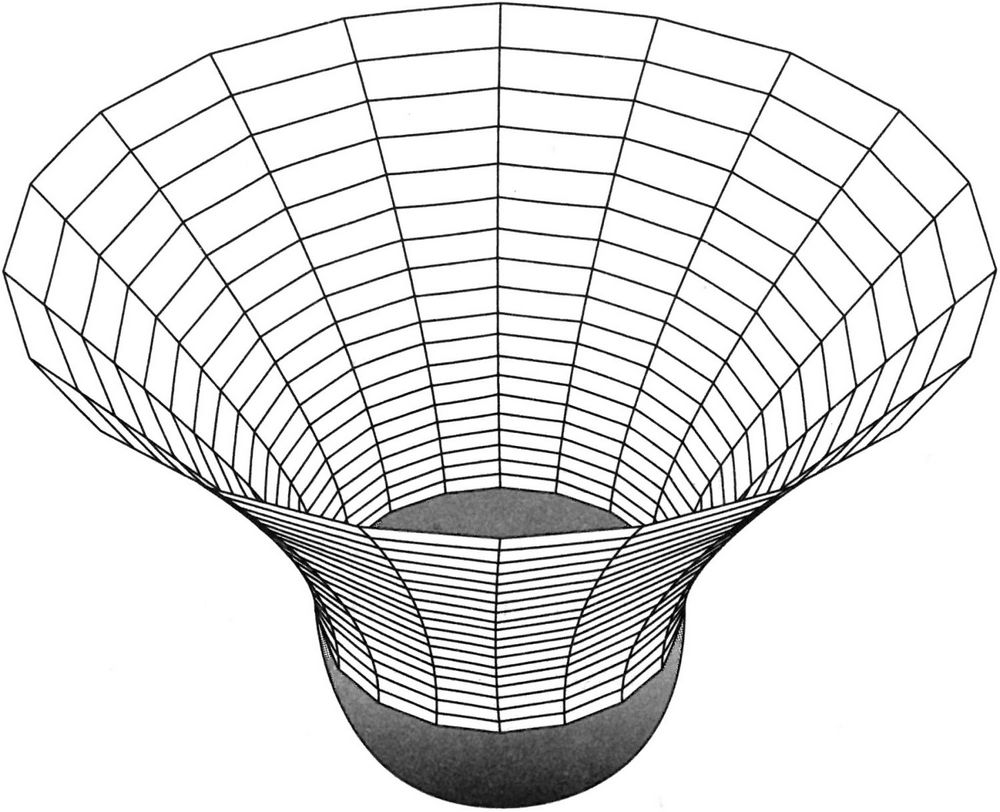
FIGURA 11.6. En la propuesta «sin límite» de James Hartle y Stephen Hawking para un estado cosmológico inicial, el tiempo (o lo que llaman «tiempo imaginario») cuando el universo es pequeño. El eje temporal de arriba abajo gira horizontalmente en la figura para crear un límite suave y redondeado, y el tiempo no tiene principio. La evolución espacio-temporal del universo primigenio parece un volante de bádminton.

Esta es la situación que Hartle y Hawking llamaron estado «sin límites» para el origen del universo, y fue la cuestión central del best seller de Hawking Historia del tiempo, publicado en 1988. El principio del universo quedaba caracterizado como un evento que no desempeñaba el papel de un límite temporal. El universo tenía un principio, pero no era un big bang de una singularidad de densidad y temperatura infinitas en la que el espacio y el tiempo quedaban destruidos. Su principio es suave y poco interesante, algo parecido a pasar andando junto al Polo Norte en la superficie de la Tierra^[404]. De hecho, la condición de no límite es una propuesta para el estado del universo si aparece de la nada^[405] en un evento cuántico. La historia de este universo es que hace mucho, mucho tiempo no existía el tiempo.

Esta fórmula no está exenta de problemas, y no es la única posibilidad de estado cuántico inicial del universo. Alex Vilenkin propuso otro estado inicial con previsiones muy distintas sobre el tipo de universo más probable para aparecer de la nada^[406]. La condición inicial de Vilenkin acababa pareciendo más razonable porque favorecía la aparición de universos muy pequeños y con temperatura y densidad muy altas, algo parecido al universo caliente que se había convertido en la imagen estándar del universo joven. Por otra parte, se halló que la formulación de Hartle-Hawking exigía que el universo más probable fuese infinitamente grande y vacío^[407].

Un universo autocreado

La única novedad en el mundo es la historia que no conoces.

Harry S. Truman

La idea de un universo sin un principio caliente con una singularidad porque la noción de tiempo se desvanece al examinar el pasado cada vez más de cerca, también se puede poner de manifiesto sin recurrir a sutilezas como la mecánica cuántica y el tiempo imaginario. Una posibilidad simple, que yo mismo sugerí en 1986, es que podría haber un universo con un pasado pero sin principio si se exigía que todas las trayectorias a través del tiempo y el espacio fuesen bucles cerrados muy grandes^[408].

Las ecuaciones de Einstein permiten la existencia de bucles cerrados que no impiden el viaje en el tiempo, como aprendimos del universo sin expansión de Gödel. Aunque no hubiese expansión, imaginemos un universo en expansión en el que todas las historias de partículas y rayos de luz son bucles cerrados con una duración total enorme (más de 100 000 millones de años). Aún no habríamos notado nada raro en este universo, pero al ahondar en el pasado acabaríamos simplemente llegando al futuro. Un universo así no tiene un principio en el tiempo. Simplemente «es», aunque, parafraseando a Bill Clinton, sí que es necesario aclarar lo que significa «es».

Esta forma de evitar el origen del tiempo la desarrollaron posteriormente con mayor detalle Richard Gott y Li-Xin Li en la Universidad de Princeton^[409]. Lo que hicieron fue modificar la teoría del universo inflacionario eterno para obtener un ejemplo de un universo del que se pudiese decir que se creó a sí mismo.

En el universo inflacionario eterno se producen continuamente nuevos universos «bebé» a partir de un universo progenitor. Si estamos en uno de los universos de esta serie, podríamos mirar hacia atrás y localizar nuestro universo «madre», y el universo madre de este, etc. Ya hemos visto que es posible —hay quien diría que es incluso lo más probable— que este seguimiento hacia atrás no termine nunca y que no exista un principio del proceso de creación de universos ni del multiverso que lo define. Pero la nueva posibilidad que sugerían Gott y Li era que, en el pasado, una de las ramas se había doblado sobre sí misma creando un bucle temporal cerrado, de modo que parece que se «crea» a sí misma. Si todas las ramas emanasen de una o más de estas «ramas incestuosas», el universo se convertiría en su propia madre y no habría principio que hallar (Figura 11.7).

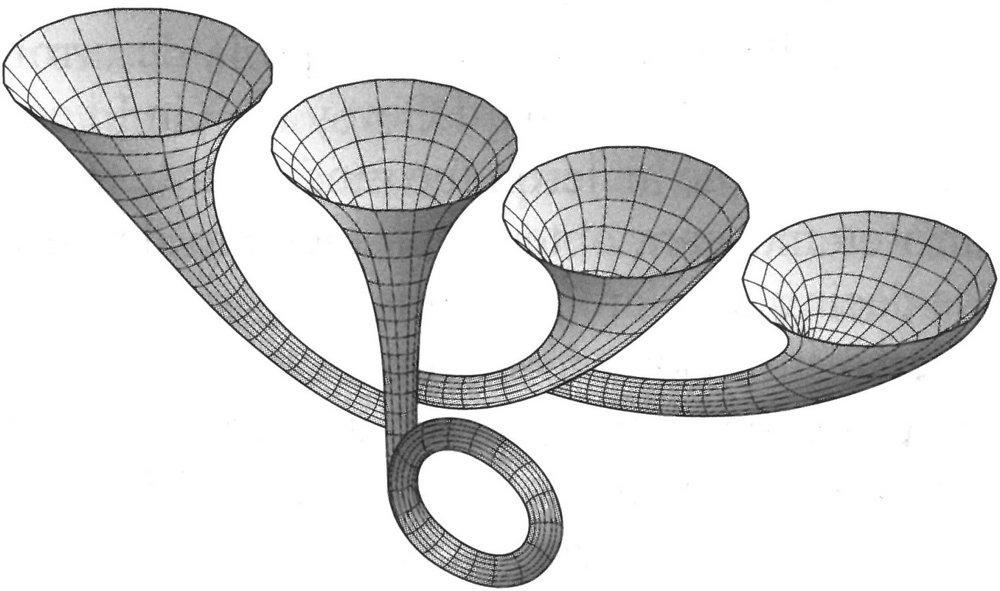
FIGURA 11.7. El universo autocreado de Gott. Un bucle en el tiempo al principio permite que este universo sea su propio progenitor. Es una contrapartida no cuántica y en tiempo real de la receta de Hartle-Hawking.

Universos en colisión

Hace poco, en la M5, un camión con la marca Malvern Water me adelantó a toda velocidad hacia el norte. Unos minutos más tarde vi un vehículo similar con la marca Highland Spring Water que iba en dirección sur. ¿Estamos todos locos?

Stephen Pimenoff^[410]

La idea de que los universos en expansión que contienen una densidad superior a la crítica puedan contraerse de nuevo hacia big crunch y «rebotar» hacia un nuevo ciclo de expansión que más adelante se contrae y rebota, y así ad infinitum, no es nueva. Fue sugerida por primera vez por Richard Tolman en 1934, como extensión del modelo de universo simple de «una oportunidad», pero Tolman señaló que la segunda ley de la termodinámica llevaría a un sistemático desplazamiento de la energía hacia formas más desordenadas, como la radiación, lo que haría que los ciclos sucesivos creciesen en tamaño y edad. Más recientemente, en 1995, Mariusz Dąbrowski y yo mismo demostramos que, si la constante cosmológica de Einstein existe, entonces, independientemente de lo pequeña que sea, siempre habrá una última oscilación y el próximo estado se convertirá en uno de expansión exponencial (véase la Figura 3.20^[411]).

En el año 2001 se renovó el interés por los universos cíclicos debido a una variante que aprovechaba nuevas posibilidades ofrecidas por la teoría de cuerdas: la propusieron Justin Khoury, Burt Ovrut, Paul Steinhardt y Neil Turok^[412] y la llamaron universo «ecpirótico» en recuerdo de los filósofos estoicos de la Grecia antigua, que abogaban por una visión cíclica del cosmos. La palabra griega ekpyrosis denota el fuego que todo lo consume, en el que los griegos creían que el universo se zambullía periódicamente antes de emerger, como un fénix, en una nueva creación.

La nueva versión de un universo cíclico proponía que existe un estado inicial natural para el universo, dictado por una máxima simetría. Las teorías de cuerdas solo producen teorías del todo autocoherentes si el universo posee más dimensiones espaciales que las tres a las que estamos acostumbrados. Para ajustar esta predicción a la experiencia, se cree que solo tres de las dimensiones se hacen lo bastante grandes, quizá porque la inflación cosmológica actúa selectivamente sobre ellas de alguna forma especial, mientras que las otras siguen siendo en la actualidad imperceptiblemente pequeñas. Esta división de dimensiones en grandes y pequeñas debe de haber sucedido muy al principio de la historia del universo, cerca de los 10⁻⁴³ s. Los defensores de la teoría ecpirótica proponían que existe un estado inicial natural en el que dos universos tridimensionales (llamados «branas»)^[413] se acercan entre sí moviéndose en una de esas dimensiones adicionales. Su movimiento es como el de dos láminas de energía perfectamente paralelas que se acercan y colisionan. En el momento de la colisión producirán una conflagración que rebotará hacia un estado de expansión. Se afirma que esta colisión y rebote no sufre las situaciones imposibles de tratar del big bang tradicional porque no hay infinitos en las magnitudes físicas, como la temperatura y la densidad, y el tejido del espacio y el tiempo sigue siendo suave. La energía liberada por la colisión se consume en la creación de partículas elementales que participan en la expansión. La esperanza es que la expansión resultante tenga lugar al ritmo crítico, y manifieste pequeñas fluctuaciones que aparecerán en los mapas de temperatura del universo que los satélites están actualmente produciendo.

¿Puede predecir esta audaz teoría alguna cosa que sea observable y, al mismo tiempo, distinta de las predicciones de la inflación? ¿Es la teoría coherente? Se trata de preguntas clave con las que los defensores siguen luchando. La teoría ofrece un escenario que puede tener una única colisión, pero también permite una serie indefinida de expansiones y recontracciones^[414]. La entropía total del universo aumenta de ciclo a ciclo, pero la cantidad total que se puede ver en la parte observable del universo no crece hasta niveles inaceptables, porque la expansión rápida acelerada que tiene lugar al principio de cada ciclo diluye la entropía producida en el anterior. Pero aún hay un problema similar con la acumulación de agujeros negros de larga duración de un ciclo al siguiente que quedan atrapados en la siguiente colisión de mundos, y con el rápido crecimiento de anisotropías en la expansión cada vez que tiene lugar la contracción^[415].

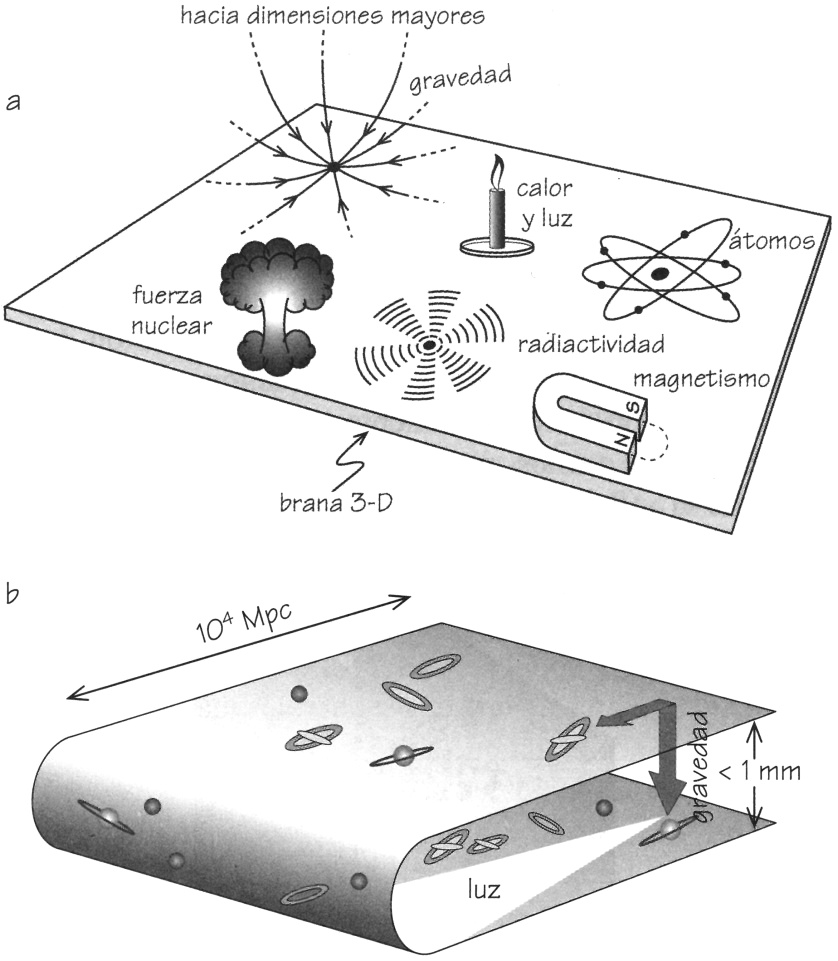
FIGURA 11.8. (a) Las fuerzas del electromagnetismo, la radiactividad y las interacciones nucleares están confinadas a una brana tridimensional, mientras que la gravedad actúa en todas las dimensiones del espacio, de modo que se ha hallado que es mucho más débil que otras fuerzas en los mundos-brana. (b) Las branas pueden ser paralelas y separadas por una distancia de menos de un milímetro, pero también pueden estar dobladas y estar separadas por distancias igualmente minúsculas. La luz viaja por la superficie plegada del espacio de la brana, pero la gravedad también actúa en dimensiones superiores, y se puede propagar por la separación entre los pliegues, creando así la apariencia de una gravedad mucho más intensa a distancias menores que la separación entre branas.

Otras versiones especulativas de la física de altas energías han incorporado consideraciones de mundos brana, pero sin colisiones cataclísmicas. Podría existir otro universo tridimensional muy cercano al nuestro si se mide en una de las dimensiones espaciales adicionales. Si la otra brana se mueve con respecto a nosotros, esto puede crear modificaciones en aspectos observables de la física: las constantes tradicionales de la Naturaleza podrían cambiar, y la inflación del universo podría verse estimulada. Pero la motivación para tener en cuenta este tipo de esquemas no es, en primera instancia, cosmológica. Se propuso que la fuerza de gravedad actúa en todas las dimensiones del espacio, pero que no es así en el caso de las otras fuerzas —fuerte, débil y electromagnética— (véase la Figura 11.8). Esto puede ofrecer alguna pista sobre la razón por la que la gravedad es mucho más débil que las otras fuerzas; e incluso, quizá, por qué parece haber mucha menos materia luminosa que materia gravitante a la vista en el universo. Nuestra brana próxima podría ser gravitatoriamente cercana pero ópticamente distante, como se muestra en el esquema de la Figura 11.9.

FIGURA 11.9. Nuestro universo podría ser una brana situada cerca de otro mundo-brana paralelo. Ambas están situadas en la superficie del «espacio volumen» global.

Al contemplar las imágenes del universo caótico y del universo eterno inflacionario, asumimos tácitamente que nuestra región había sufrido una gran inflación, mucho más que la extensión de nuestro actual horizonte visible. Es posible, aunque algo antinatural, que si la cantidad de inflación fuese únicamente (por coincidencia) suficiente para explicar lo que vemos, podríamos estar ya encontrándonos con los efectos de la inflación de un tipo distinto que tuvo lugar «en la vecindad». En tal caso, podríamos buscar los efectos de una burbuja vecina afectando a nuestra propia expansión. En última instancia habría efectos importantes que distorsionarían por completo la expansión que podemos ver y la isotropía de la radiación de fondo. Pero ¿y los efectos del primer contacto con una burbuja ajena? Se han hecho algunos intentos de predecir lo que podríamos ver si una burbuja tocase de refilón el límite de nuestro universo y dejase «cicatrices». Deberíamos buscar bandas en el patrón de temperaturas de la radiación en el cielo, un probable efecto de este evento^[416]. Michael Salem ha efectuado una simulación, y el efecto de bandas en la radiación de fondo de microondas se ilustra en la Figura 11.10. Pero esto es solo el escenario más simple; si las burbujas nos afectan de formas más complicadas podría haber físicas muy distintas (o solo antimateria) que producirían efectos catastróficos al contactar con nuestra propia burbuja. Por suerte, se calcula que es altamente improbable que los universos se pongan a colisionar en la noche, ¡pero antes también creíamos que era muy improbable que la Tierra colisionara con asteroides y cometas!

FIGURA 11.10. Bandas de temperatura que se crearían en la radiación de fondo de microondas por la colisión de refilón de dos «universos-burbuja».

La muerte de la luz

Dylan Thomas^[417]

Ya hemos visto que, en varias ocasiones, los cosmólogos han explorado la posibilidad de que las constantes de la Naturaleza tradicionales cambien con el tiempo, o incluso varíen de un lugar del universo a otro. La posibilidad más radical de este tipo la desarrollamos, en 1998, Andy Albrecht, João Magueijo y yo mismo^[418]. En ella especulábamos con lo que sucedería si la velocidad de la luz cambiase en las primeras etapas del universo. Esta idea resultó tener diversas consecuencias interesantes, idénticas a las provocadas por un breve brote de inflación o por una expansión acelerada. Si hubo un breve período en los primeros momentos de la historia del universo en el que cayó el valor de la velocidad de la luz, la expansión se vería impulsada hacia la división crítica entre universos abiertos y cerrados, los monopolos quedarían eliminados y las irregularidades compensadas^[419]. Todos estos resultados son altamente apetecibles, y ofrecen otra solución para los diversos problemas a los que los cosmólogos se enfrentaban durante la década de 1980. También parece reducir la influencia del término de la constante cosmológica en las últimas fases de la expansión, algo que la inflación no puede hacer^[420].

Este escenario atípico no requiere cambio residual alguno de la velocidad de la luz en la actualidad. El cambio en la velocidad de la luz necesario para producir estos resultados podía haber ocurrido fugazmente, como la inflación, cuando la edad del universo no era más que de 10⁻³⁵ segundos. El reto consistía en encontrar la forma de generar fluctuaciones en la densidad del universo que pudiesen formar las semillas de las galaxias y manifestarse mediante las fluctuaciones de temperatura que crean en la radiación de fondo. La inflación podía hacer ambas cosas y tenía un aspecto más atractivo. Se han intentado generar fluctuaciones de otras formas en teorías cosmológicas como estas, pero aún no han sido exploradas a fondo^[421].

Los esquemas en los que la velocidad de la luz varía se denominan cosmologías VSL («varying speed of light», velocidad de la luz variable, en inglés). Estos esquemas muestran hasta qué punto los cosmólogos se han abierto a la idea de que las antes sacrosantas constantes fundamentales puedan variar. Uno de los motivos para esta liberalización de los puntos de vista es el modo en que se han visto surgir muchas constantes en las teorías de cuerdas. La enorme multiplicidad de estados de vacío hallados en esas teorías se traduce en que hay innumerables «juegos» de constantes distintos que producen universos posibles y autocoherentes. Las constantes parecen objetos ordinarios que pueden adquirir todo tipo de valores distintos y pueden cambiar si el universo evoluciona de un estado de vacío a otro. Su estatus en el esquema global de las cosas se ha reducido de forma significativa. Este cambio de actitud se ha visto reforzado por otra nueva perspectiva del universo que degrada aún más el estatus de nuestras «constantes» y nos invita a buscar las verdaderas constantes de la Naturaleza fuera de las dimensiones del espacio y el tiempo que experimentamos directamente.

Hiperuniversos

C. S. Lewis, El león, la bruja y el armario

La búsqueda de una nueva Teoría del Todo guio a los primeros teóricos de las cuerdas a un notable descubrimiento: las teorías unificadas solo eran posibles si había más dimensiones espaciales de las tres a las que estábamos habituados en la vida cotidiana. La introducción de la idea de que hay más de tres dimensiones ha abierto nuevas y numerosas posibilidades. De hecho, las teorías de cuerdas y la más profunda «teoría M» permiten que haya más de una dimensión temporal. Estas teorías solo existen si la dimensión total del espacio y el tiempo tiene un valor específico, generalmente 10 u 11. Se suele interpretar que el significado de esto es que hay nueve o diez dimensiones espaciales y una de tiempo. Sin embargo, la teoría no especifica separación alguna entre el espacio y el tiempo: podría existir igualmente si hubiera tres dimensiones temporales y siete u ocho espaciales. Simplemente suponemos que solo hay un tiempo porque las cosas se hacen realmente extrañas con más de uno: las partículas inestables se desintegran muy rápidamente, la energía desaparece y el futuro no está determinado de forma única y completa por el presente. Es extraño, pero no es imposible desde el punto de vista lógico ni incoherente desde el punto de vista físico. Lo más probable es que la vida compleja no pudiese evolucionar en un universo de doble tiempo, pero quizá los otros tiempos pueden ser sutilmente inocuos por ser su ámbito muy breve, de solo minúsculas dimensiones espaciales adicionales.

Podría ser que hubiese universos lógicamente posibles con diferentes divisiones espacio-tiempo en el paisaje de posibles estados de vacío para el universo. Los resultados de la inflación podrían también contener distintas posibilidades para la división entre espacio y tiempo, y también para el número de dimensiones que sufren inflación y se hacen grandes. En tal caso, sospechamos que nosotros deberíamos encontrarnos en una con una división de dimensiones temporales y espaciales de 1 + 3. En ambos casos, las opciones que fijan el número de tiempos y espacios, así como el número de dimensiones espaciales que se hacen grandes, pueden quedar determinadas de forma totalmente aleatoria o ser dictadas por algún principio aún desconocido.

La propiedad más edificante de estos desarrollos de la física fundamental que nos hacen tomarnos en serio las dimensiones espaciales adicionales es que el espacio tridimensional que nos rodea y al que llamamos «el universo» es únicamente la sombra de una verdadera realidad multidimensional. Todas las cantidades a las que llamábamos «constantes de la naturaleza», por ejemplo, no son realmente fundamentales en absoluto. Las verdaderas constantes existen en nueve o diez dimensiones, y solo vemos una parte de ellas proyectada en nuestras tres dimensiones. En consecuencia, nuestras denominadas «constantes» ni siquiera tienen por qué ser constantes. Si las dimensiones adicionales tiemblan o cambian de tamaño muy lentamente, veríamos cambiar nuestras constantes tridimensionales al mismo ritmo. Es por eso por lo que hay un enorme interés por la búsqueda observacional de posibles variaciones en algunas de las constantes de la Naturaleza mediante la astronomía y los experimentos de laboratorio de precisión^[422]. Existe incluso un creciente corpus de datos de quasars que es muy coherente con una pequeña variación en la constante que determina la intensidad de la electricidad en algunas partes por millón a lo largo de 10 000 millones de años^[423]. Las variaciones en las constantes tradicionales de la Naturaleza son una potente ventana a través de la cual contemplar las dimensiones adicionales. Otros físicos tienen esperanzas de que los eventos detectados en el LHC (Large Hadron Collider, Gran colisionador de hadrones) ofrezcan pruebas a favor o en contra de la idea de que existe otro universo brana muy próximo al nuestro en el que pueden desintegrarse partículas y dejar el rastro revelador de energía desapareciendo misteriosamente del espacio. Lo más interesante acerca de estas especulaciones es que no son descabelladas: se las puede someter a prueba y restricción experimental mediante aceleradores de partículas y potentes telescopios astronómicos situados en la Tierra y en el espacio.