5 

Algo totalmente distinto

Una vez me encontré con el filósofo Richard Rorty, parado de pie con aspecto aturdido en el mercado de Davidson. Me dijo en susurros que acababa de ver a Gödel en el pasillo de congelados.

Rebecca Goldstein^[165]

Un universo de queso suizo

Debo admitir mi decepción cuando leí que el número de teléfono de Einstein era el 2807.

Michael Mahler

En la década de 1940, el estudio de los universos se paralizó por completo. La generalización de la guerra supuso la reasignación de los físicos y matemáticos a los campos de la investigación armamentística, la meteorología, la aeronáutica y la criptografía. Las universidades se cerraron a la llegada de nuevos estudiantes, y los contactos internacionales se restringieron, limitándose a los aliados más próximos. Einstein estaba en Estados Unidos, y muchos otros grandes científicos alemanes habían huido a Gran Bretaña y a América. El universo nunca había parecido tan pequeño.

FIGURA 5.1. Ernst Straus (1922-1983).

Llegado 1944, Einstein había reclutado a un nuevo ayudante en Princeton. Sus asistentes eran siempre jóvenes matemáticos de talento, capaces de compensar la debilidad en ese campo que el propio Einstein confesaba. Ernst Straus era una especie de prodigio de las matemáticas. Empezó por tomar interesantes atajos para calcular secuencias de números con solo cinco años, descubriendo el truco que permite sumar mentalmente los 100 primeros números en cuestión de segundos^[166]. Había nacido en Múnich en 1922 pero, con la llegada al poder de los nazis en 1933, su familia emigró a Palestina, donde recibió su educación en un instituto y en la Universidad Hebrea de Jerusalén. Straus no se quedó a terminar su licenciatura, sino que, con menos de 20 años, se trasladó a la Universidad de Columbia en Nueva York en 1941 para iniciar investigaciones de doctorado. En 1944 se vio contratado como nuevo asistente de investigación de Einstein en el Instituto de Estudios Avanzados de Princeton^[167].

El joven Straus no tenía formación en física, y sus gustos matemáticos se inclinaban hacia la teoría de números y cuestiones de matemática «pura», pero no vaciló en llenar las vacantes dejadas por las partidas de Nathan Rosen (1935-1945) y Leopold Infeld (1936-1938). Llegada la primavera de 1945, Einstein y Straus habían hallado un nuevo tipo de universo posible a partir de las ecuaciones de Einstein^[168]. Se trataba de un universo muy similar a uno de los universos en expansión simples de Friedmann y Lemaître, que contenía materia (como galaxias) que no ejercía presión. Pero este universo tenía huecos esféricos, como las burbujas de un queso suizo (Figura 5.2). Cada hueco vacío tenía una masa en el centro, igual en magnitud a la masa «excavada» para crear el hueco. Se trataba de un paso hacia un universo más realista, en el que la materia no estaba distribuida suavemente con la misma densidad, sino reunida en acumulaciones, como galaxias, dispersos por el espacio vacío.

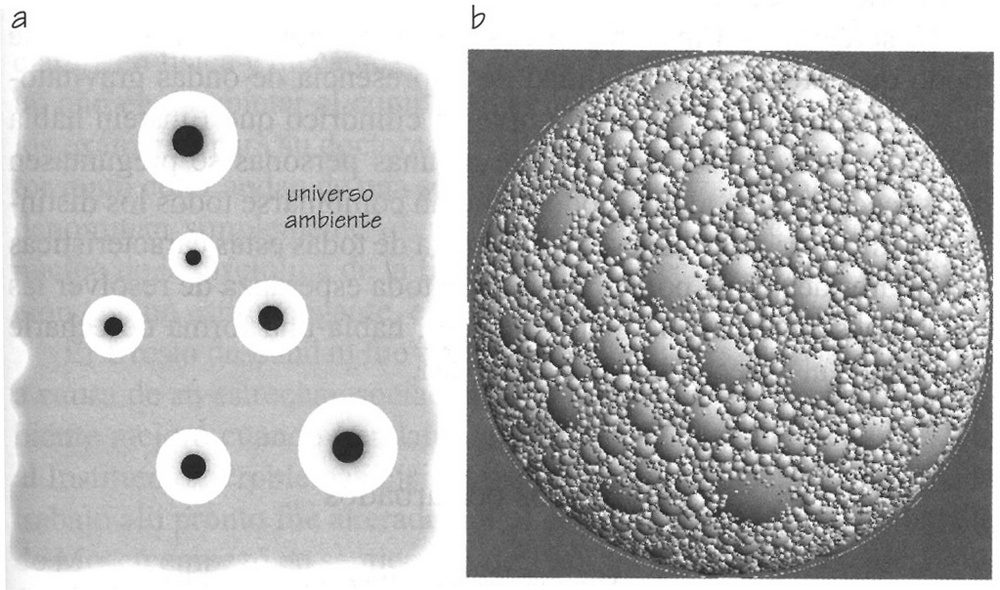
FIGURA 5.2. (a) El modelo de universo de queso suizo. Las regiones esféricas son evacuadas, dejando toda su masa en un paquete esférico en sus respectivos centros, (b) Un universo de queso suizo generado por ordenador, creado por Allen Attard, de la Universidad de Toronto. Empieza con una densidad uniforme; a continuación se marcan 34 667 esferas de distintos tamaños y cada una de ellas se comprime hasta un punto en sus respectivos centros; el 80 por ciento del espacio está contenido en los huecos esféricos.

Cada uno de los «huecos» era esférico, y este nuevo universo de queso suizo podía adaptarse al universo no uniforme de Tolman eligiendo el conjunto adecuado de condiciones iniciales. Como siempre, el descubrimiento de una solución exacta para un sistema de ecuaciones tan difícil y complejo como el de Einstein suponía el uso de alguna simplificación en la solución para que las ecuaciones fuesen manejables. Y sin embargo, esto recuerda un poco a la frase famosa de Groucho Marx sobre que no quería pertenecer a un club que lo aceptase como miembro^[169]: cualquier solución de las ecuaciones de Einstein lo bastante simple como para poder hallarla contendrá invariablemente alguna característica especial que la convertirá en atípica o sin interés.

La solución de Einstein y Straus era simple porque era esférica, de modo que excluía la posibilidad de la presencia de ondas gravitatorias, a diferencia del caso del universo cilíndrico que Einstein había hallado con Rosen. Esto hizo que algunas personas se preguntasen qué sucedería si de algún modo pudieran combinarse todos los distintos tipos de irregularidades. La presencia de todas estas características irregulares acabaría, por supuesto, con toda esperanza de resolver las ecuaciones de Einstein. Y sin embargo, había una forma de echarle una ojeada al aspecto de un universo así.

Universos perturbados

—Algunos árboles, Watson, crecen hasta una cierta altura y entonces desarrollan una antiestética excentricidad.

Arthur Conan Doyle^[170]

En la Unión Soviética se habían efectuado pocos avances en cosmología desde el notable descubrimiento de los universos en expansión de Friedmann a principios de la década de 1920. La teoría de Einstein se consideraba indisolublemente unida a las cuestionables filosofías idealistas contrarias a los dictados del materialismo dialéctico^[171]. Y la funesta dictadura de Stalin ya era suficiente preocupación para todos. El más notable de los físicos teóricos del país, Lev Landau, fue arrestado e internado en prisión por actividades antisoviéticas durante la Gran Purga, en 1938-1939. Solo lo liberaron por la persuasiva intervención de físicos de fama internacional como Peter Kapitsa y Niels Bohr.

Landau se había convertido en profesor del nuevo Instituto Psicotécnico de Ucrania, en Kharkov, en 1933, con solo veintisiete años de edad. Había efectuado excepcionales contribuciones a la física desde su adolescencia, y terminaría obteniendo el premio Nobel en 1962 por su explicación del comportamiento superfluido del helio a bajas temperaturas^[172]. En la nueva universidad, la reputación de Landau atrajo a destacados estudiantes, y Landau estableció nuevos estándares para la enseñanza avanzada de la física. Su estudiante más conocido era un joven de Kharkov llamado Eugene Lifshitz. Lifshitz terminó su licenciatura en física y mecánica a los dieciocho años, y tardó poco más de un año en completar el complicado curso de Landau y superar todos los exámenes para su doctorado^[173]. Años más tarde, Lifshitz sería coautor junto con Landau de una serie de textos avanzados, que los físicos denominan simplemente «Landau y Lifshitz», que establecieron el núcleo de la disciplina de la física teórica necesaria para la investigación con un estilo elegante, económico y unificado.

El arresto de Landau fue potencialmente un desastre para Lifshitz, a causa de su estrecha asociación con su mentor^[174]. Por suerte, el ambiente mejoró cuando Landau fue liberado y se trasladó con Lifshitz al Instituto de Problemas Físicos de Moscú. Sin embargo, el ritmo de trabajo allí pronto fue alterado por el estallido de la guerra. La batalla de Moscú empezó en septiembre de 1941 y duró hasta enero de 1942. Con la ciudad enfrentada al colapso y la hambruna, muchas personas huyeron hacia el este o fueron evacuadas. Muchos de los físicos fueron trasladados a Kazán. A Moscú lo salvaron los elementos: una intensa lluvia y un frío glacial, algo para lo que las tropas alemanas estaban mal preparadas, detuvo el avance. Fue en este período de dificultades y privaciones cuando Lifshitz empezó a estudiar un nuevo problema cosmológico. Como Friedmann anteriormente, su motivación era matemática, no astronómica.

Hemos visto que los científicos se habían empezado a interesar por lo que sucede en universos que no son isótropos ni uniformes en el espacio, como los hallados por Friedmann, Lemaître y De Sitter. Kasner y Tolman primero, y luego Einstein, Rosen y Straus, habían empezado a explorar las propiedades de los universos que difieren en una dirección o en otra o de un lugar a otro. Estos universos son claramente más realistas, porque el universo no es perfectamente liso e idéntico en todas direcciones.

Lifshitz abordó el problema de una forma muy común en física: se toma la solución exacta simple de la teoría y se examina qué sucede si se cambia en una cantidad muy pequeña. ¿Exigen las ecuaciones que estos pequeños cambios se debiliten con el paso del tiempo, o crecen y se amplifican? Si los pequeños cambios disminuyen, esto nos indica que el universo simple que hemos decidido perturbar es estable y no evoluciona hacia uno con una estructura muy diferente. Sin embargo, si los pequeños cambios crecen con el paso del tiempo, nuestro universo simple es inestable y evolucionará hacia un estado muy distinto en el futuro.

En su artículo de 1946, publicado en ruso, Lifshitz examinaba lo que sucede si se perturban ligeramente los universos isótropos y homogéneos de Friedmann^[175]. Al parecer, dio a este problema un tratamiento puramente matemático, y no lo relacionó con la cuestión de por qué en el universo hay irregularidades, como las galaxias. Mostró cómo se pueden crear tres tipos distintos de pequeñas irregularidades. El primero consistía simplemente en variar ligeramente la densidad de un lugar a otro; el segundo era hacer rotar la materia lentamente; el tercero era introducir una pequeña ondulación de ondas gravitatorias en el espacio liso. Cuando sus efectos son muy pequeños, estos distintos fenómenos no se mezclan en un turbulento embrollo, como sí sucede cuando son grandes. Sus efectos permanecen independientes y son fáciles de extraer. Si tomamos una bola esférica y le aplicamos estas tres perturbaciones, la primera correspondería a variar su densidad y forma, la segunda sería hacerla rotar y la tercera sería aplastarla como un elipsoide pero sin modificar su volumen.

Lifshitz mostró que las pequeñas diferencias de densidad tienden a hacerse más pronunciadas a medida que pasa el tiempo. Newton también lo había comprendido a finales del siglo XVII cuando, en una carta a Richard Bentley, director (y tirano) del Trinity College de Cambridge durante muchos años, le señaló que, si una distribución perfectamente suave de materia adquiría una ligera irregularidad, las regiones más densas atraerían más materia a expensas de las regiones menos densas, y la situación se haría cada vez más irregular. A esto se le llama «inestabilidad gravitatoria» (Figura 5.3). Sus efectos se notan con bastante rapidez en una distribución de materia en el espacio que no se esté expandiendo. Lifshitz mostró que sigue sucediendo en un universo en expansión, pero la irregularidad crece más lentamente debido a que la acumulación de las partículas de materia se opone al efecto contrario de la expansión que las separa. También mostró que, si nos fijamos en acumulaciones lo bastante pequeñas, el proceso de incremento de la irregularidad acaba por detenerse si hay alguna presión que se le oponga. La imagen global era simple: si se empieza con un universo casi isótropo y homogéneo, las desviaciones de la uniformidad se hacen cada vez más pronunciadas a medida que el universo se expande^[176]. Este fue el primer cálculo que demostraba que los universos isótropos y homogéneos eran especiales. El hecho de que, tras miles de millones de años de expansión, las inuniformidades del universo sigan siendo pequeñas en promedio implica que al principio, hace 14 000 millones de años, debían de ser extraordinariamente pequeñas.

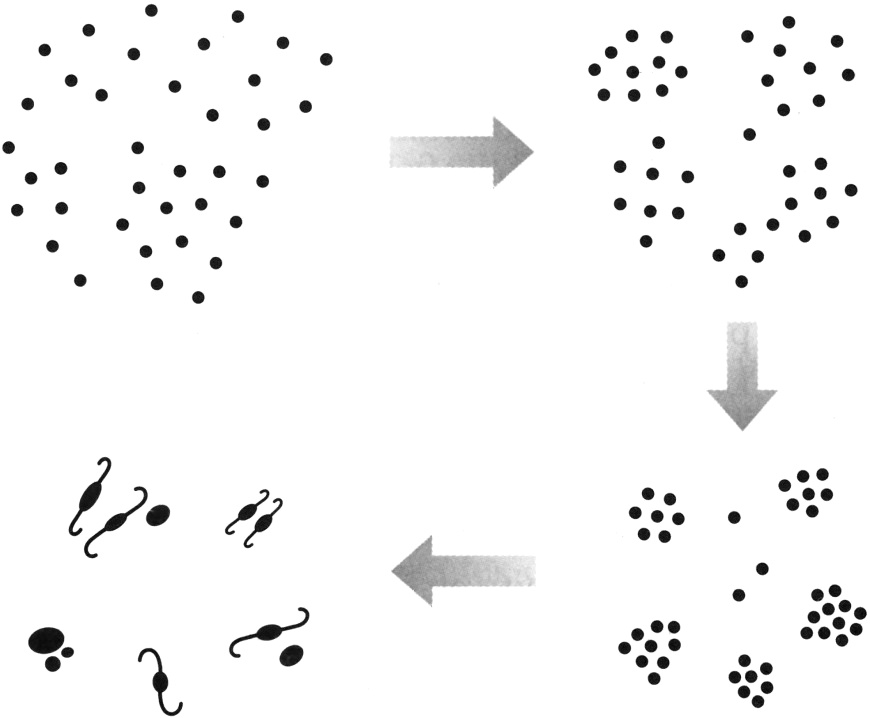
FIGURA 5.3. La gravedad transforma gradualmente una distribución ligeramente no uniforme en otra cada vez con más grumos. Las regiones más densas ejercen más tirón gravitatorio y acrecen más materia adicional a costa de las menos densas.

Poco a poco, otros astrónomos intentaron utilizar estos cálculos para llegar a una explicación para la existencia en el universo de estructuras como las galaxias. Por desgracia, esas explicaciones no eran totalmente convincentes. Para que las irregularidades creciesen hasta formar galaxias, había que elegir un nivel especial de irregularidad que existiese en algún momento cercano al principio de la expansión. Y sin embargo, no había ninguna buena razón para que existiese tal irregularidad de ningún nivel especial en ningún momento, de modo que, en realidad, la explicación no explicaba nada.

En el caso de los otros tipos de irregularidad en los cálculos de Lifshitz, se podía demostrar que cualquier vórtice grande de materia en rotación girará más lentamente a medida que el universo se expande. Más adelante, algunos cosmólogos sacarían de aquí la conclusión de que debían de haber sido inmensos en el pasado distante, lo que sugería que todas las galaxias en rotación que vemos actualmente debían de haberse formado a partir de una caótica turbulencia primordial. Por último, las ondas gravitatorias que Einstein y Rosen habían luchado por interpretar correctamente aparecían también como una posible perturbación de pequeño tamaño en un universo perfectamente liso. Los cálculos de Lifshitz mostraban que la fuerza de estas ondas disminuía a medida que el universo se expandía y hacía que las ondas se estirasen.

Los cálculos de Lifshitz, tomados en principio como ejercicios matemáticos, supusieron un hito en el estudio de los universos. Desde entonces se han repetido docenas de veces en formas distintas, y los resultados se han utilizado para determinar las signaturas de los tres tipos de pequeñas perturbaciones cuando observamos la radiación de fondo o los procesos de agrupación de galaxias. Se han dedicado libros enteros a sus consecuencias, y nos ofrecen una forma de entender cómo se desarrollan las irregularidades en el universo cuando sus inicios son pequeños.

El universo de Schrödinger

En el futuro todo es una onda, en el pasado todo es una partícula.

Lawrence Bragg^[177]

Mientras Einstein revolucionaba nuestra concepción global del universo, tuvo lugar una transformación aún más rápida de nuestra comprensión de la materia a escala subatómica. La aparición de la mecánica cuántica como nueva forma de entender el comportamiento de la materia y de la luz le debía mucho a Einstein, pero aún más a Niels Bohr, Werner Heisenberg, Paul Dirac, Max Born, Wolfgang Pauli y Erwin Schrödinger. Con paso seguro, esta disciplina reveló la estructura de los átomos y las moléculas, explicó la Tabla Periódica de elementos y predijo multitud de propiedades de los sólidos. Y sin embargo, no tenía intersección alguna con la cosmología. Dirac había tenido sus escarceos cosmológicos, pero no utilizó para nada la mecánica cuántica en sus afirmaciones de que la fuerza de la gravedad podía disminuir a medida que el universo envejecía. Lemaître tenía una cierta idea del modo en que el universo había emergido a partir de una especie de estado inicial superdenso al que denominó «átomo primordial». Para comprenderlo habría sido necesario combinar la mecánica cuántica con la teoría de la gravedad de Einstein, pero Lemaître no sabía cómo hacer algo así. Algunos físicos se preguntaban si la creación de materia se podía describir mediante la nueva mecánica cuántica, y Richard Tolman lanzó la vaga especulación de que los centros de las galaxias podían ser las fuentes de una continua interconversión de materia y radiación. Ninguna de estas especulaciones condujo a ninguna parte, pero un notable físico se las arregló para ofrecer una primera incursión en la idea de un universo cuántico.

La ecuación que halló Erwin Schrödinger en 1926 y que lleva su nombre es la más importante de las ecuaciones de la física matemática. Sus soluciones describen toda la estructura atómica y molecular, toda la ciencia de materiales y la química. Schrödinger era el hijo único de una familia acaudalada, y sus padres reconocieron sus capacidades y le facilitaron tutores privados. Se convirtió en un estudiante de éxito en la Universidad de Viena, en donde también enseñó, antes de ocupar puestos de profesor en Zúrich, Berlín, Oxford y Dublín. Compartió el premio Nobel de Física con Paul Dirac en 1933.

En su vida personal, Schrödinger era bastante heterodoxo. Su breve estancia en el Magdalen College de Oxford, en 1933, y los intentos de ofrecerle una plaza en Princeton el año siguiente, se complicaron por su deseo de establecerse con su mujer y con su amante; los tres estaban a su vez implicados en romances con otros físicos y sus cónyuges. Finalmente acabó por trasladarse a Graz, Austria, en 1936, pero fue invitado a Dublín en 1940 por el Taoiseach (primer ministro) irlandés Éamon de Valera, para unirse al nuevo Instituto de Estudios Avanzados de Dublín, fundado con una intención similar a lo que se había establecido en Princeton para Einstein. Schrödinger aceptó, pero el fin de su carrera en Dublín quedó marcado por diversos escándalos menores por aventuras con mujeres casadas y por hijos ilegítimos. Si el estilo de vida de Schrödinger era algo excesivo para el Oxford de los años treinta, sin duda era demasiado para el Dublín de los años cincuenta. Schrödinger murió en 1961, y está enterrado en el cementerio parroquial del hermoso pueblo tirolés de Alpbach, rodeado por el paisaje alpino que amaba. En su lápida está grabada la ecuación de Schrödinger (Figura 5.4).

Schrödinger se tomó un interés entusiasta en los universos en expansión de la teoría general de la relatividad de Einstein. Su primera incursión en el estudio de los universos fue un intento de ver qué es lo que la mecánica cuántica tenía que decir al respecto. Para ello decidió investigar lo que sucede con las ondas en un universo en expansión^[178]. Los resultados ofrecieron información, no solo sobre el comportamiento de las ondas ordinarias de sonido y de luz, sino sobre la variedad de ondas cuánticas que nos indican la probabilidad de observar eventos específicos^[179].

FIGURA 5.4. La tumba de Erwin Schrödinger (1887-1961), en la localidad austríaca de Alpbach, lleva una inscripción con la ecuación de Schrödinger.

Schrödinger hizo un importante descubrimiento que nadie (ni siquiera él mismo) supo apreciar del todo en aquel momento. La expansión del universo podía transformar su energía cuántica del vacío en partículas reales y mesurables. Cuando no hay expansión, las partículas y las antipartículas aparecen continuamente y desaparecen de nuevo en forma de radiación. La energía se conserva, y esta imagen de actividad febril describe el vacío cuántico. Sin embargo, si este vacío se expande con la suficiente rapidez, o si está sujeto a una fuerza gravitatoria que varía de forma muy pronunciada en una distancia muy corta, esas partículas y antipartículas que aparecen del vacío pueden experimentar fuerzas tan distintas que no se aniquilan de nuevo en forma de radiación. El resultado es que aparecen partículas y antipartículas reales y mesurables, a partir de la energía que impulsa la rápida expansión o las variaciones de la gravedad de un lugar a otro. Este asombroso fenómeno de producción de partículas en un universo en expansión se estudió profundamente desde mediados de la década de 1970, después del espectacular descubrimiento de Stephen Hawking según el cual esto mismo tendría lugar en el borde de un agujero negro, lo que tendría como resultado finalmente la pérdida de toda la masa del agujero^[180].

En aquel momento, Schrödinger no pensó que el proceso fuese muy importante en un universo en expansión, porque sus efectos son en la actualidad inconmensurablemente pequeños e irrelevantes para comprender el fenómeno de la expansión. No obstante, en los primeros momentos de la expansión, cuando el ritmo de esta era fabulosamente alto y la densidad de radiación cerca de 10¹²⁸ veces mayor que la actual, los efectos de producción de partículas descubiertos por Schrödinger habrían sido realmente significativos. Podrían incluso explicar ciertas propiedades del universo. En la década de 1970, se afirmaba que muchas de las asimetrías e irregularidades de la expansión quedarían reducidas o totalmente eliminadas por el proceso de producción de partículas, porque este proceso se alimenta de las diferencias de energía de una dirección a otra o de un lugar a otro, amortiguándolas de forma gradual.

Sin embargo, en 1939 los cosmólogos aún no estaban preparados para la teoría cuántica. Si los físicos hubieran sido receptivos, quién sabe cuáles podrían haber sido las consecuencias. Pero Einstein se oponía decididamente a la teoría cuántica («Dios no juega a los dados», dice su célebre cita) y se habría resistido con todo su empeño a que se aplicase al universo en su conjunto. La creación de partículas, sin embargo, pronto se convertiría en un asunto controvertido, como veremos en el próximo capítulo.

El universo rotatorio de Gödel

La visión teológica del mundo es la idea de que el mundo y todo lo que contiene tiene un sentido bueno e indudable. […] Como nuestra existencia terrena tiene en sí un sentido muy dudoso, la consecuencia directa es que solo puede tratarse de un medio hacia el objetivo de otra existencia. La idea de que todo en el mundo tiene un significado es precisamente análoga al principio de que todo tiene una causa, idea sobre la que reposa la totalidad de la ciencia.

Kurt Gödel^[181]

Cuando Einstein envejeció y su obra dejó de resolver problemas antiguos o de plantear otros nuevos, solía decir a la gente que si iba a la oficina era «solo por tener el privilegio de regresar a casa paseando con Kurt Gödel». Gödel fue uno de los mejores matemáticos del siglo XX, y el lógico más importante desde Aristóteles. Nacido en Brno, en el antiguo Imperio Austrohúngaro, en 1906, un año después de que Einstein publicase las teorías de la relatividad especial, del movimiento browniano y del efecto fotoeléctrico, Gödel se matriculó en la Universidad de Viena en 1924 para estudiar física, pero pronto quedó seducido por las matemáticas. Gödel impresionó a sus profesores, y pronto fue invitado a unirse al legendario grupo de debate, el Círculo de Viena, que se reunía en cafeterías para hablar de filosofía, lógica y ciencia y que, en diversas épocas, contó con Ludwig Wittgenstein, Bertrand Russell y Karl Popper. Sin embargo, Gödel era la excepción en este grupo: era el único miembro que no creía que la experiencia fuese la única fuente de conocimiento y que la lógica matemática fuese la única herramienta para la resolución de problemas filosóficos.

La fama de Gödel se debe principalmente a su demostración del teorema de incompletitud de la aritmética que, para el asombro general de matemáticos y filósofos, demostraba que sistemas lógicos tan ricos como la aritmética contienen siempre afirmaciones cuya verdad o falsedad no se pueden establecer utilizando únicamente las reglas del propio sistema. Este teorema tiene multitud de consecuencias inesperadas; por ejemplo, que ningún programa informático que no modifique el sistema operativo de un ordenador puede detectar todos los programas que lo hacen. En consecuencia, ningún programa antivirus puede hallar todos los virus posibles en un ordenador, a menos que interfiera con el sistema operativo y lo modifique.

Como Einstein, Gödel llegó al Instituto de Estudios Avanzados de Princeton huyendo del auge del fascismo en su país. Visitó por primera vez el Instituto en 1933-1934, pero no regresó al año siguiente tras sufrir una especie de crisis mental^[182]. Gödel acabó yéndose de Viena con su mujer en otoño de 1939, después de sufrir el ataque de unos nazis cerca de la universidad, probablemente porque pensaron que era judío. Sin embargo, tomó la ruta más larga imaginable para llegar a Princeton: atravesó Asia en el ferrocarril Transiberiano, luego tomó un barco de Japón a San Francisco, donde llegó en marzo de 1940, y finalmente viajó en tren a través de Estados Unidos hasta Princeton.

En 1942, Gödel ya era un gran amigo de Einstein. Ambos tenían un origen cultural similar y gran interés por la filosofía, algo que los diferenciaba de los científicos norteamericanos que los rodeaban, y podían conversar en alemán.

En diversas ocasiones, Gödel prometió a Einstein que escribiría algunas de sus ideas acerca de la teoría de la relatividad, pero no surgió nada apasionante de esto hasta 1947. Las cartas de Gödel a su madre en aquellos momentos contaban que estaba absorbido por su trabajo y que en verano de 1947 había hecho un descubrimiento notable. Para sorpresa de todos, había estado trabajando en hallar una nueva solución a las ecuaciones de Einstein. El resultado sorprendió incluso a Einstein.

El universo de Gödel era un universo en rotación (Figura 5.5). No se expandía, y toda la materia giraba a un ritmo constante alrededor de un eje que señalaba en una dirección. Contenía la constante cosmológica de Einstein, pero con valor negativo, de manera que reforzaba la atracción gravitatoria de la materia, que contrarrestaba el efecto de empuje de la materia hacia fuera por causa de la rotación. Esto ya era lo bastante interesante de por sí, pero el universo de Gödel tenía otra propiedad totalmente inesperada: permitía el viaje en el tiempo. Gödel mostró que había caminos en el espacio y el tiempo que eran bucles cerrados. La mayor parte de las personas, Einstein incluido, esperaban que algo así sería contrario a las otras leyes de la física y permitiría que se produjesen contradicciones lógicas, del tipo «matarse a uno mismo de niño», que suelen aparecer en las películas de ciencia ficción^[183]. Y sin embargo, resulta que el viaje en el tiempo está permitido en la teoría de Einstein y no se contradice con ninguna otra de las leyes de la Naturaleza conocidas. Freeman Dyson recordaba haber oído algo acerca de ello en su primer encuentro con Gödel, siendo un joven recién llegado a Princeton en 1948:

Era septiembre de 1948. Había llegado como joven miembro al Instituto de Estudios Avanzados. Para mi gran asombro, una de las primeras personas a las que conocí fue el mismísimo Kurt Gödel que, por si esto fuera poco, me invitó a su casa. El caso es que me sentí un privilegiado. Gödel resultó ser una persona amable y sociable, en absoluto como yo me lo había imaginado. ¡Y cuerdo! De manera que me invitó a su casa y hablamos sobre física. Resulta que era un gran conocedor del asunto y que, de hecho, había trabajado en física, porque hacía unos años Einstein le había planteado que examinase los universos en rotación, y eso fue precisamente lo que hizo. Yo estaba algo sorprendido porque, por una parte, Gödel era un matemático fabuloso cuyos trabajos en este campo habían sacudido los cimientos de la matemática […] y hasta dónde llegaría una persona así […] me pareció asombroso que hiciera algo comparativamente tan trivial como demostrar que esos universos en rotación existían, lo cual no era un aspecto demasiado interesante de la física. Él mismo era consciente de ello; puesto que no era ningún ignorante en el terreno de la física, sabía que no se trataba de la línea central de la disciplina. Pero en fin, así fueron las cosas. Nos reunimos muchas veces más, y él solía preguntarme: «¿Lo han encontrado ya? ¿Saben ya si el universo estaba en rotación?». Pensaba que esto podía verificarse mediante observaciones, y yo tenía que darle la noticia de que las observaciones estaban muy lejos, a un factor de un millón, de ser capaces de poder decidir, pero siempre quedaba decepcionado. Cada vez que me llamaba por teléfono solía preguntar «¿Lo han encontrado ya?». Y yo siempre tenía que decirle que no^[184].

FIGURA 5.5. Universo de Gödel. La materia gira alrededor de un eje central con velocidad angular constante. La rotación afecta a los conos de luz que aparecen cuando los rayos de luz salen de cada punto. Conforme nos alejamos del centro, los conos de luz se inclinan y se abren porque la velocidad de rotación lineal aumenta. Existe una distancia especial desde el centro de rotación a la que los conos de luz se inclinan hasta ser tangentes al plano, y luego se asientan sobre él de modo que los rayos de luz pueden viajar por debajo del plano hacia el pasado. Supon que tu planeta estaba antes en p y ahora está en q. Puedes volver a visitar p acelerando hacia un punto fuera del círculo crítico y luego viajando hacia abajo por debajo del plano original a través de p, a continuación dirigirte al círculo crítico debajo de p y finalmente ir hacia el futuro en dirección a p. Aunque siempre te has dirigido hacia «tu» futuro has acabado en tu pasado.

FIGURA 5.6. Einstein y Gödel en Princeton.

Mirando hacia atrás, el descubrimiento de Gödel, que se publicó con el título Un ejemplo de un nuevo tipo de solución cosmológica a las ecuaciones de campo gravitatorio de Einstein, tuvo gran importancia en nuestro estudio de los universos^[185]. Reveló que el universo podía tener unas propiedades globales extraordinarias que, simplemente, no se mostraban localmente. El hecho de que las cosas pareciesen ordinarias en el sistema solar no significaba que el espacio y el tiempo no pudiesen enredarse de formas extrañas en la escala del universo entero. Aunque el universo de Gödel no se expandía como el universo que podemos observar, sus peculiares propiedades temporales aún podían estar presentes en otros universos rotatorios que sí se expanden y que se parecen a nuestro universo.

Al principio, diversos físicos distinguidos no aceptaron que el universo de Gödel admitiese el viaje en el tiempo, pero en realidad no comprendían el carácter de estos viajes, y las deducciones de Gödel acabaron por confirmarse. En algunos de sus escritos, Gödel parecía hallar un cierto atractivo en la posibilidad de evitar la muerte sacando provecho de la circularidad del tiempo; un colega lo halló una vez escribiendo hacia atrás en su pizarra para escenificarla. Por desgracia, el viaje en el tiempo en el universo de Gödel requiere velocidades próximas a las de la luz y configuraciones de materia extremadamente antinaturales. No parece una propuesta demasiado práctica para viajeros espaciales. También hay que tener presente que el universo de Gödel no es una manifestación de Regreso al futuro. No se puede modificar el pasado. Como señaló Samuel Butler, ni siquiera Dios puede cambiar el pasado; eso solo pueden hacerlo los historiadores. Supongamos que memorizo Macbeth de Shakespeare y viajo al pasado para encontrarme con Shakespeare de joven, antes de que escribiese alguna de sus obras. Allí le relato con gran detalle el texto y la trama de Macbeth. Shakespeare recuerda cada una de las palabras, las escribe y publica Macbeth. ¿De dónde ha venido Macbeth? Yo la aprendí de Shakespeare y él la aprendió de mí. No ha tenido un principio. Simplemente existe.

Las paradojas lógicas del tipo «qué pasaría si matase a mi abuela» constituyen un género que los filósofos interesados en el viaje en el tiempo^[186] denominan «paradojas de la abuela», y parecen amenazar cualquier forma de viaje hacia atrás en el tiempo^[187]. Han formado una parte importante de los relatos de ciencia ficción sobre viajes en el tiempo desde que la idea apareciese en 1895 en el clásico de H. G. Wells The Time Machine (La máquina del tiempo).

¿Deberíamos convencernos de que estos ejemplos de «cambiar el pasado» revelan algún aspecto fundamentalmente imposible sobre el viaje en el tiempo? No. Cambiar el pasado es algo no del todo coherente. El pasado fue el que fue. No se puede modificar y esperar que el presente que has experimentado siga existiendo. No puede haber dos pasados. Si pudieses viajar hacia atrás en el tiempo para impedir tu nacimiento, no estarías aquí para viajar hacia atrás en el tiempo con esa finalidad.

Generalmente pensamos en el paso del tiempo como algo lineal. En el viaje en el tiempo, esta línea se cierra y se convierte en un círculo (Figura 5.7). Imaginemos una fila de personas caminando una detrás de otra. Está muy claro quién está delante y quién detrás de cada uno. Esto es el tiempo lineal: siempre se puede decir sin ambigüedades si un evento se encuentra en el futuro o en el pasado.

Supongamos ahora que la fila de personas está caminando en círculo. Localmente, está claro si alguien está delante o detrás de uno, pero globalmente las ideas de «delante de» o «detrás de» no tienen ningún sentido si se piensa en todo el círculo; cualquier persona está al mismo tiempo delante y detrás de cualquier otra. Ya no puede decirse que alguien está delante o detrás de otra persona. Simplemente hay un orden definido^[188].

Y lo mismo sucede en las historias de viajes en el tiempo. No existe una noción de pasado y futuro sin ambigüedades, sino únicamente una secuencia lógicamente coherente de eventos a lo largo de un bucle de tiempo cerrado. Lo que es, es y lo que fue, fue. Uno puede formar parte del pasado, pero no puede cambiarlo. La experiencia personal se repetirá periódicamente si uno vive lo suficiente.

He aquí un ejemplo de una historia de viaje en el tiempo coherente. Imagine que viaja hacia atrás en el tiempo y se prepara para dispararse a sí mismo siendo un bebé. Está decidido a crear una paradoja factual en el universo. Se apunta mientras su madre lo sostiene en sus brazos. Empieza a presionar el gatillo, cuando una herida de su hombro, causada por el hecho de que su madre lo dejó caer siendo un bebé, le envía un espasmo por el brazo y hace que el disparo no acierte en el objetivo. Pero el sonido del disparo basta para asustar a su madre, que deja caer al bebé, causándole una lesión en el hombro. La coherencia en las historias hace que los universos sean seguros para los historiadores.

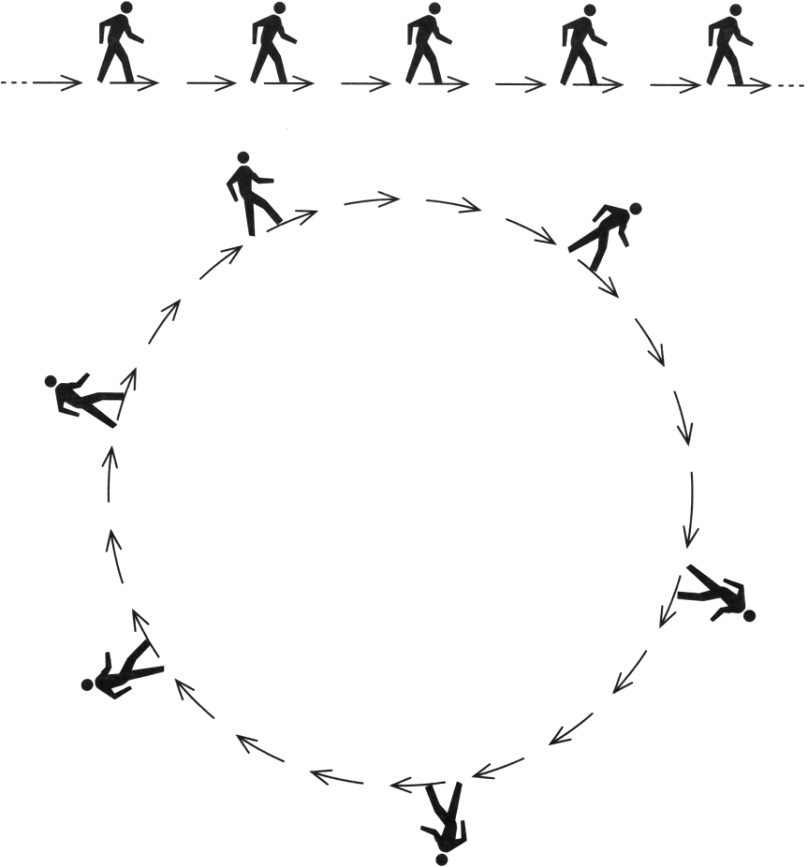
FIGURA 5.7. Personas que se mueven una tras otra, en línea recta y en círculo. En la línea recta, cada persona está o bien delante o bien detrás de todas las demás. En el círculo, todos están a un tiempo delante y detrás de todos los demás.

Gödel fue impulsado a descubrir su universo en rotación por su deseo de mostrar que el paso del tiempo no es objetivo: no hay un estándar temporal absoluto. Su universo es extraño porque siempre tiene el mismo aspecto desde cualquier punto (hay una rotación constante y no hay expansión), pero no hay ningún estándar externo contra el cual medir la rotación (porque el universo incluye todo lo que existe). Gödel calculó cuidadosamente a qué velocidad habría que viajar para completar un viaje cerrado en el tiempo, y pasó largos períodos reuniendo datos acerca de la distribución de las galaxias en el cielo porque estaba convencido de que el universo resultaría estar girando. Lamentablemente, nuestro universo no es el universo de Gödel. Se está expandiendo, y si está en rotación, esta es muy lenta. Es fácil comprobarlo, porque la radiación que nos llega desde distintas direcciones sufriría cambios distintos en su intensidad, y estas diferencias no pueden ser mayores de una parte en 100 000^[189]. Del mismo modo que la rotación de la Tierra causa que su forma se aplane, la rotación del universo crea una distorsión en el perfil de temperaturas de la radiación procedente del cielo, más caliente a lo largo del eje de rotación y más fría en ángulo recto con él.

Quizá el descubrimiento de Gödel no ofreciese una descripción viable de nuestro propio universo en expansión, pero nos condujo a nuevas expectativas acerca de cosas extraordinarias que podían ocultarse en las ecuaciones de Einstein. Los universos podían poseer propiedades globalmente muy estrambóticas, a pesar de tener un aspecto local totalmente inocuo. El universo de Gödel mostraba que la rotación podía distorsionar el espacio de una forma tan extrema que las historias temporales se cerraban. Gödel mostró que las ecuaciones de Einstein permitían la existencia de universos con propiedades que no tenían homologas newtonianas.

Por desgracia, Gödel nunca volvió a publicar trabajos sobre cosmología. Sus intereses quedaron absorbidos por los problemas más complejos de la lógica y la filosofía. Los cosmólogos pasaron mucho tiempo intentando averiguar cómo había llegado a su solución, pero Gödel había sido muy cuidadoso al cubrir sus huellas. Era un hombre extraño.