7 

Universos, verrugas y todo eso

Soy el gato que camina solo y a quien no le importa estar aquí o allá.

Rudyard Kipling, Just So Stories

Universos turbulentos

Cuando muera y vaya al cielo, hay dos asuntos para los que espero obtener la iluminación. Uno es la electrodinámica cuántica, y el otro es el movimiento turbulento de los fluidos. Soy bastante optimista sobre el primero de ellos.

Horace Lamb^[222]

Con solo algunas excepciones aisladas, la tendencia general de los primeros estudios sobre universos derivados de la teoría de Einstein se había centrado en los que eran suaves y uniformes, y que se expandían al mismo ritmo en todas direcciones. Este sesgo se debía a dos motivos de peso. Por un lado, se adaptaba bastante bien a las observaciones a través de telescopios astronómicos. No había pruebas de diferencias en el ritmo de expansión en una dirección u otra, y el mecanismo de agrupación de galaxias no parecía diferir mucho de la simple aleatoriedad en todo el cielo. En los primeros tiempos, el proceso de medición del corrimiento hacia el rojo llevaba mucho tiempo. Para medir unos pocos corrimientos era necesario pasar casi toda la noche en el telescopio. Hasta la aparición de detectores fotométricos basados en la tecnología CCD utilizada en las cámaras de vídeo en la década de 1970 (que supuso el premio Nobel de Física de 2009) no fue posible medir un gran número de corrimientos hacia el rojo con rapidez. Este cambio permitía que las observaciones de situación de posiciones de galaxias en el cielo pudiesen ahora incluir sus corrimientos (y así deducir la distancia a las galaxias), a fin de crear una imagen tridimensional de la distribución de galaxias. Los mapas tridimensionales resultantes supusieron una sorpresa mayúscula, y revelaron que las posiciones proyectadas en el cielo eran indicadores engañosos de la riqueza y la sutileza de la agrupación de galaxias en una telaraña cósmica de línea y láminas^[223].

Hemos visto cómo la introducción de «principios» como el Principio Cosmológico o el Principio Cosmológico Perfecto se utilizó para dar a estas hipótesis simplificadoras una cierta base filosófica, si es que era necesaria. Sin embargo, también hay buenas razones para intentar ir más allá en el camino de un mayor realismo en las descripciones del universo. Después de todo, el universo real contiene galaxias y otras irregularidades en la distribución de materia. ¿De dónde vienen estas irregularidades? ¿Por qué tienen las formas y tamaños que tienen? Aunque las desviaciones de la isotropía perfecta en la expansión parecían muy reducidas, no podían ser igual a cero si es que rechazamos la idea de que ocupamos una ubicación especial en el universo. Si el espacio no es uniforme, no puede ser isótropo para todos sus puntos.

Lemaître había sido el primero en pensar seriamente en el origen de las galaxias, y el artículo de Lifshitz acerca de la estabilidad del universo en expansión en presencia de pequeñas desviaciones de la uniformidad perfecta ofrecía una clave importante sobre las razones por las que el universo contenía tantas acumulaciones de materia en forma de estrellas y galaxias. Las regiones que contenían ligeramente más materia que la media atraerían aún más materia a expensas de las regiones menos densas. Este proceso de inestabilidad gravitatoria, comprendido en primer lugar por Newton y calculado en detalle por Sir James Jeans en 1902, actúa con gran rapidez en una región del espacio que no se expande ni se contrae. No obstante, como descubrió Lifshitz, si la región se expande, el ritmo de crecimiento de la irregularidad se reduce. La aglomeración de materia tiene que vencer la tendencia global de la expansión, que procura dispersarla, así que la reducción del ritmo de crecimiento de la irregularidad no representa sorpresa alguna.

Los cosmólogos se preguntaban si este proceso simple es capaz de explicar en última instancia por qué existen galaxias en el universo. Quizá hubiera al principio algunas variaciones «aleatorias» muy pequeñas respecto de la suavidad perfecta, o quizá fueran creadas por algún proceso específico poco después, y simplemente se hicieron cada vez mayores hasta separarse de la expansión global y se estabilizaron para formar las estructuras que hoy denominamos «galaxias». Pero esta explicación aún es bastante pobre. ¿Por qué las galaxias suelen contener entre 100 000 millones y un billón de estrellas? ¿Por qué sus formas son particularmente una variedad de elipses y espirales? Y lo más sorprendente de todo, ¿por qué muchas de ellas giran?

Durante el período de 1944 a 1951, el físico alemán Carl von Weizsäcker empezó a pensar en la posibilidad de que muchas de las estructuras del universo fuesen restos de un pasado mucho más turbulento. Es una idea atractiva. La turbulencia es muy conocida y omnipresente. Basta con levantar el tapón de la bañera para ver un rápido flujo turbulento de agua; cuando observamos las olas del mar, o las hojas girando en el viento después de que pase un coche acelerando, y ahí está de nuevo (Figura 7.1). Y sin embargo, esta familiar experiencia representa un problema prácticamente intratable para los matemáticos que estudian el flujo de líquidos. Cuando el flujo es rápido y turbulento, es muy difícil comprender claramente lo que está sucediendo. Si el flujo es lento y la turbulencia más o menos suave, podemos esperar un cierto avance; en caso contrario, nuestros ordenadores y nuestra capacidad de cálculo sufren una amarga derrota ante la complejidad del problema. Uno de los premios de un millón de dólares que el Instituto Clay ofrece por la solución de alguno de los llamados Problemas del milenio, los siete mayores problemas matemáticos sin resolver, está precisamente esperando la solución de este enigma^[224].

FIGURA 7.1. Flujo de aire turbulento detrás de un avión a reacción.

Von Weizsäcker estaba interesado en tratar de explicar el origen del sistema solar^[225] y los movimientos de las estrellas en las galaxias^[226]. Luego, intrigado por las imágenes de galaxias espirales que sugerían que su aspecto de torbellino podía deberse a un anterior período más turbulento de la historia del universo, sugirió que la turbulencia debía ser la clave para entender la existencia de galaxias^[227]. En esta cruzada tuvo la compañía de su paisano Werner Heisenberg, uno de los arquitectos de la mecánica cuántica, que desarrolló una teoría matemática de la turbulencia y siguió fascinado por el fenómeno durante toda su carrera^[228].

A George Gamow también le seducía esta imagen de un universo que había sido turbulento, y propuso una teoría similar en 1952^[229]. Pero, aunque es fácil imaginar el surgimiento de las galaxias de un revoltijo turbulento, no es tan sencillo convertir esta idea en una teoría exacta. La turbulencia no se comprendía en el laboratorio, ni desde luego en el universo en expansión, aunque al menos en este entorno las cosas sucedían más lentamente y los vórtices de materia giraban en el espacio sin fronteras restrictivas, boquillas y desagües que hacen que las turbulencias en el cuarto de baño sean tan complicadas.

Lifshitz había mostrado que los vórtices débiles decaerían en las últimas etapas del universo, pero sus velocidades permanecerían constantes durante la fase de radiación caliente. La razón para ello es la misma que la que explica por qué una patinadora que realiza una pirueta gira más rápido al acercar sus brazos al cuerpo, y más lento al separarlos. En un gran remolino giratorio en un universo en expansión, los «brazos» se estiran y se separan y, a medida que el remolino crece, la velocidad de rotación de la materia se reduce^[230].

La turbulencia tiene una propiedad simple y singular: si se crea mediante la agitación de grandes vórtices en un líquido, entonces su energía cae en cascada a vórtices cada vez más pequeños, hasta que llega un momento que son lo bastante reducidos como para disolverse por efecto de la fricción del fluido. Una forma de ver esta caída en cascada es dejar caer una gota de tinta en un vaso de agua y agitar muy suavemente. En 1941, el gran matemático ruso Nikolai Kolmogorov había propuesto que entre las dimensiones más grandes en las que la turbulencia se creó en primer lugar y las más pequeñas en las que queda amortiguada por la viscosidad del fluido, la energía se debe transferir de los vórtices más grandes a los más pequeños a un ritmo constante^[231]. En consecuencia, la velocidad de rotación de los remolinos giratorios de la turbulencia debería ser proporcional a la raíz cúbica de su diámetro^[232] para una amplia gama de tamaños, independiente del modo en que se originó la turbulencia y de cómo se disipa en las escalas más pequeñas debido a la fricción. Se trata de una propiedad atractiva, porque esta característica variación de la velocidad con el tamaño de los remolinos giratorios se puede asociar con la velocidad de rotación de galaxias de distintos tamaños. Pero la historia de un universo turbulento es mucho más compleja.

Durante los primeros 300 000 años de la expansión del universo, la velocidad del sonido es muy alta, y los movimientos en el vórtice habrían sido subsónicos. Sin embargo, después de que los electrones y los protones se unan para formar átomos, la radiación deja de interactuar con los electrones y la velocidad del sonido cae de forma radical. De pronto, los vórtices pasan a girar a velocidades supersónicas, lo que genera acontecimientos cataclísmicos. Se forman colosales ondas de choque, y la materia queda amontonada en grandes irregularidades. A partir de este apilamiento de materia giratorio inducido por las ondas de choque se supone que se forman las galaxias. Cuando las cosas se estabilicen, esperamos encontrarnos con grandes galaxias en rotación.

Este escenario ofrecía la posibilidad de explicar la existencia y la rotación de las galaxias como consecuencia del patrón especial de turbulencia indicado por Kolmogorov, siempre que se pudiera explicar el origen de la turbulencia cósmica y comprender el apilamiento supersónico de materia.

El apoyo de Gamow al universo turbulento no atrajo demasiados seguidores, y la teoría cayó en desuso hasta mediados de la década de 1960, cuando algunos importantes grupos de investigación dirigidos por Hidekazu Nariai en Hiroshima y por Leonid Ozernoy en Moscú empezaron a desarrollar la teoría de forma independiente. Entre 1964 y 1978 se dedicó mucho esfuerzo a esta búsqueda, y siguió siendo una teoría viable para el origen de las galaxias hasta finales de la década de 1970. El estudio de este esquema de universo era complicado, porque era muy difícil hallar una solución a las ecuaciones de Einstein que describiese un universo turbulento real. Lo único que se podía hacer era seguir el rastro de los vórtices formados poco después del principio del universo y comprobar que habían sobrevivido y creado irregularidades en la densidad y la presión a partir de las cuales pudiesen formarse islas de material en rotación que, de algún modo, acabasen pareciéndose a las galaxias que vemos en el cielo.

La idea acabó pereciendo debido a la aparición de dos grandes problemas. Al principio, parecía como si los vórtices turbulentos no tuvieran que afectar demasiado a la expansión del universo. Por desgracia, resultó que no era así. Aunque los vórtices tenían la misma velocidad cuando se seguía su historia hacia atrás, su efecto gravitatorio sobre la expansión del universo no hacía más que crecer. En última instancia, debía de haber un momento en el pasado en el que todo el universo no era más que un caótico revoltijo turbulento. Para que la velocidad de rotación de los vórtices fuese suficiente para producir las galaxias que vemos actualmente, este estado de caos turbulento habría tenido lugar en un momento demasiado reciente como para ajustarse a nuestras observaciones de la radiación de fondo. También quedaría en entredicho la síntesis del helio, que ha producido las abundancias observadas actualmente, cuando la edad del universo era de unos tres minutos^[233].

El segundo gran problema de estos escenarios turbulentos era la necesidad de un cambio radical en nuestros conocimientos sobre galaxias en rotación. Hasta 1974, los astrónomos creían que todas las galaxias elípticas rotaban, y que su forma era más plana cuanto más rápida fuese la rotación. James Binney, un estudiante asociado de investigación en Oxford, mostró que no era necesaria la rotación para explicar el achatamiento de las galaxias elípticas^[234]. Lo más probable era que sus estrellas se moviesen en órbitas aleatorias, y la forma global era consecuencia del proceso de formación. Poco a poco, las observaciones empezaron a sostener esta perspectiva: las velocidades de rotación de galaxias elípticas resultaron ser demasiado bajas para explicar sus formas planas, y algunas incluso giraban alrededor del eje equivocado. Estos dos datos, considerados en conjunto, acabaron rápidamente con la teoría turbulenta de la formación de galaxias. Por desgracia, la turbulencia tiene un efecto demasiado drástico sobre la expansión del universo y provocaría que fuese terriblemente irregular y distorsionado, algo que sería complicado conciliar con la expansión suave y casi perfectamente esférica que vemos hoy en día.

Universos distorsionados: de uno a nueve

El propósito de cualquier Teoría Cosmogónica es buscar condiciones idealmente simples que podrían haber dado inicio al mundo y a partir de las cuales, por acción de las fuerzas conocidas, podría haber resultado ese mundo en toda su complejidad.

Georges Lemaître^[235]

El estudio de los universos hasta 1950 había estado dominado por las distintas variedades de universo que son iguales en todas partes y que se expanden al mismo ritmo en todas direcciones, los denominados «homogéneos» (iguales en todos los lugares) e «isótropos» (iguales en todas direcciones). Son los más simétricos, de modo que son las soluciones más fáciles de hallar y de comprender de las ecuaciones de Einstein. Ocasionalmente se hallaba algún universo de una clase distinta, como los descubiertos por Kasner, Einstein y Rosen o Straus, Tolman y Gödel, o se investigaba el comportamiento de minúsculas distorsiones de la uniformidad y la isotropía, como las investigaciones pioneras de Georges Lemaître y Evgeny Lifshitz. Pero estos universos anómalos se habían descubierto de forma casi aleatoria. No se sabía demasiado cuántos de ellos podía haber y a qué categorías podían pertenecer. Todo esto cambió en 1951, cuando Abraham Taub (1911-1999) completó un sistemático y trascendental estudio de todos los universos que son iguales en todos los lugares del espacio pero pueden expandirse a ritmos diferentes en distintas direcciones^[236]. Te encuentres donde te encuentres en un universo así, se observa la misma historia. Igual que el gato que camina solo de Kipling, todos los lugares tendrían el mismo aspecto para los astrónomos de estos universos, estuvieran donde estuviesen. Sin embargo, al mirar en direcciones distintas se percibirían diferencias. El más simple de estos universos fue hallado por primera vez por Edward Kasner en la década de 1920, pero ¿cuántos otros tipos de universo que fuesen iguales en todas partes pero cuyo aspecto fuese distinto en una dirección o en otra podía haber?

En mi primer puesto de investigación postdoctorado en la Universidad de California-Berkeley en 1977, Abraham (o «Abe», como se le solía llamar) Taub era director del grupo de investigación sobre relatividad general en el Departamento de Matemáticas. Yo estaba en el Departamento de Astronomía, pero solía ir al Departamento de Matemáticas para asistir a seminarios y almuerzos informales organizados por el grupo de investigación de Taub. Los jóvenes científicos se sentían intimidados por Taub debido a la extraordinaria amplitud de sus conocimientos y de su experiencia, su inquisitiva crítica y su alergia a hablar de temas triviales: no era la persona adecuada con la que compartir ideas concebidas a medias. Había organizado el Laboratorio de informática en Berkeley, trabajado con Von Neumann en Princeton e interactuado con Einstein y Gödel; era una autoridad mundial en ondas de choque e hidrodinámica, y un experto en la teoría general de la relatividad y en cosmología, y había completado su doctorado en Princeton, bajo la supervisión de Robertson, en 1935. También manejaba su seminario con un estilo inquisitorial de la vieja escuela: no dejaba pasar ni una sola frase del ponente si él tenía alguna duda al respecto; trataba en este aspecto de la misma forma a ganadores del premio Nobel y a sus estudiantes de postgrado. Al principio parecía una persona malhumorada, pero poco a poco te dabas cuenta de que, en realidad, le gustaba ayudar: trataba a los jóvenes investigadores como si fuese el padre de una gran y potencialmente rebelde familia a la que se debía mantener en cintura.

En 1951, Taub se dio cuenta de que, en 1898, el gran geómetra italiano Luigi Bianchi (1856-1928) había resuelto el problema de hallar todos los espacios posibles que serían percibidos como iguales por observadores ubicados en cualquier lugar dentro de ellos^[237]. Las diferencias direccionales deben tener el mismo aspecto desde cualquier punto de observación. Bianchi (Figura 7.2), que pasó toda su carrera como profesor en diversas instituciones matemáticas de élite en Pisa, mostró que solo había nueve posibilidades, a las que etiquetó con los números romanos I al IX.

Taub pudo emplear la clasificación de Bianchi para hallar todos los tipos de espacio que podían ser compatibles con universos en expansión que eran iguales en todas partes^[238]. La escalera romana de posibilidades, desde el espacio I al espacio IX, establecida por Bianchi iba desde las geometrías euclidianas planas más simples, como el universo de Kasner, a los espacios isótropos curvados de Riemann y Lobachevsky, y seguía por nuevos tipos de espacio curvados de formas distintas en direcciones diferentes. Algunos podían incluso cambiar de curvatura con la expansión del universo, comportándose la mayor parte del tiempo como un universo de curvatura negativa «abierto» pero pasar ocasionalmente a mostrar curvatura positiva. Algunos, como el universo de Gödel, solo podían rotar, pero otros podían rotar y expandirse de una forma distorsionada.

Taub no pudo resolver las ecuaciones de Einstein para todos estos posibles universos, aunque sí pudo hacerlo para algunos de ellos, y escribió el universo de Kasner en la forma simple que ya hemos visto. Los más complicados de estos universos están descritos por ecuaciones que actualmente siguen sin solución, pero el comportamiento general de casi todas las posibilidades se ha ido haciendo cada vez más claro a lo largo de los pasados cincuenta años. Los «universos de Bianchi», como se denominan, empezaron a estudiarse de forma intensiva en la década de 1960, y siguieron estando en el centro de interés hasta finales de la década de 1980, a causa de la necesidad de comprender por qué razón la radiación de fondo era tan isótropa en todo el cielo.

FIGURA 7.2. Luigi Bianchi (1856-1928).

Los universos de expansión anisótropa de Taub pueden poseer cuatro propiedades esenciales que los hacen más complejos y exóticos que los universos simples de Friedmann, Lemaître y De Sitter:

1. Distorsión de corte
2. Rotación
3. Velocidades relativas a la expansión esférica de Hubble
4. Curvatura anisótropa

La primera de estas propiedades corresponde a tomar una bola esférica y apretarla por arriba y por abajo para que se deforme y adquiera forma de huevo. Mientras que un universo isótropo en expansión es como una serie de esferas, cada una mayor que la anterior, un universo con distorsión de corte es como una serie de elipsoides de volumen creciente (Figura 7.3). Los universos que giran deben también sufrir una distorsión de corte en su expansión (Figura 7.4). Es bastante simple visualizar esta combinación de propiedades. El tercer ingrediente es más sutil. Imaginemos una bola en expansión. Una de las formas de seguir la pista a esta expansión es trazar líneas rectas que radien hacia el exterior desde el centro. Podemos usar la longitud de estas líneas —AB o BC, por ejemplo— como medida del tiempo transcurrido desde el inicio de la expansión (Figura 7.5).

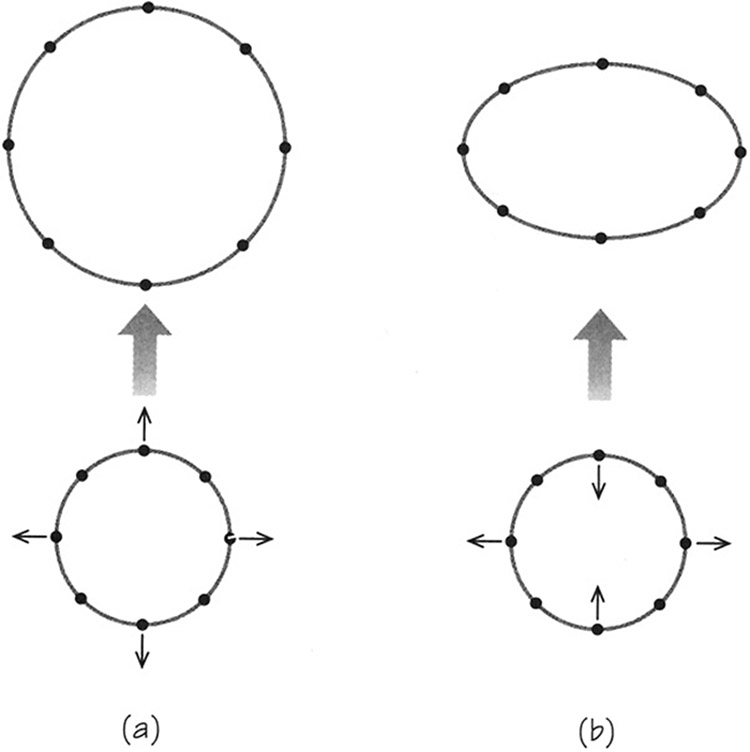
FIGURA 7.3. La acción de corte distorsiona las esferas y las convierte en elipsoides: (a) expansión sin distorsión de corte; (b) expansión con distorsión de corte.

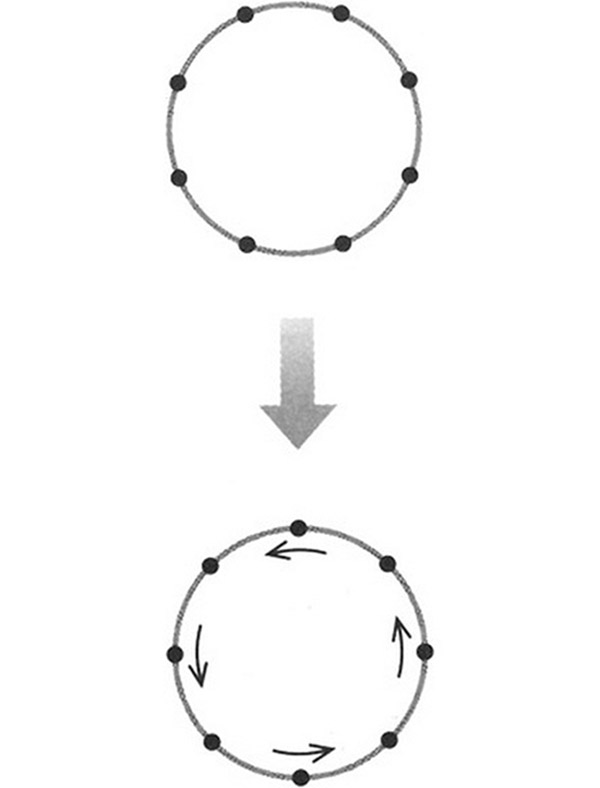
FIGURA 7.4. La acción de rotación hace girar las esferas.

FIGURA 7.5. Un universo en expansión isótropa, pero con una galaxia en E que se mueve en relación a la expansión global.

La tendencia ha sido suponer que nosotros (y otros observadores en sus estrellas de sus galaxias) también nos movemos a lo largo de esas líneas radiales imaginarias. Sin embargo, no hay motivo para pensar que deban seguir la expansión global (lo que los cosmólogos llaman el «flujo de Hubble»). Nuestro cúmulo de galaxias puede estar moviéndose hacia el exterior en una dirección distinta, o puede haber otros diversos movimientos aleatorios en marcha. Si estos otros movimientos son relativamente lentos, como el nuestro alrededor del sistema solar o el del sistema solar dentro de la Vía Láctea, o implican cantidades reducidas de materia, no tendrán ningún efecto discernible en el curso de la expansión global del universo. Sin embargo, si implican vastas cantidades de materia en movimiento rápido en relación con el flujo de Hubble promedio, pueden empezar a afectar a la expansión del universo y provocar una distorsión de corte.

Vamos a aclarar la idea con una analogía simple. Supongamos que nuestro universo en expansión tiene solo dos dimensiones espaciales y es como la superficie de un globo. Si se colocan hormigas dormidas en la superficie del globo y este se hincha, las hormigas se separarán a un ritmo estable. Forman parte de la expansión de su universo —la superficie del globo—. Pero si las hormigas se despiertan y empiezan a caminar mientras el globo se hincha, tendrán un movimiento adicional relativo entre sí que no será simplemente debido a la expansión general de su espacio. Si demasiadas hormigas caminan hacia un mismo lugar provocarán una depresión en la superficie de goma del globo y cambiarán la forma como este se expande en esa dirección.

La última de las cuatro características es una nueva posibilidad que ofrece la teoría de Einstein. No tiene homólogo en la simple imagen newtoniana del universo como gran bola en expansión. Los tres efectos que acabamos de describir pueden surgir si la expansión se inicia a ritmos distintos en diferentes direcciones, como si la elasticidad del globo que hinchamos fuese distinta en cada dirección.

Ya hemos visto que la esencia de la teoría de la gravedad de Einstein es que el movimiento de masa y energía cambia la geometría del espacio y lo dota de curvatura. En los universos isótropos simples hallados por Friedmann y Lemaître esta curvatura, como la propia expansión, era isótropa, es decir, la misma en todas direcciones. Algunos de los universos revelados por Taub poseían la nueva propiedad de que la curvatura de su espacio podía diferir en cada dirección (Figura 7.6). El más simple de los universos anisótropos, hallado por Edward Kasner, tiene expansión anisótropa, pero en cada momento el espacio es plano y su curvatura isótropa. Resulta que esta es una situación especial. Los más complicados de entre los espacios de Bianchi tienen tanto expansión anisótropa como curvatura anisótropa del espacio en cada punto del tiempo.

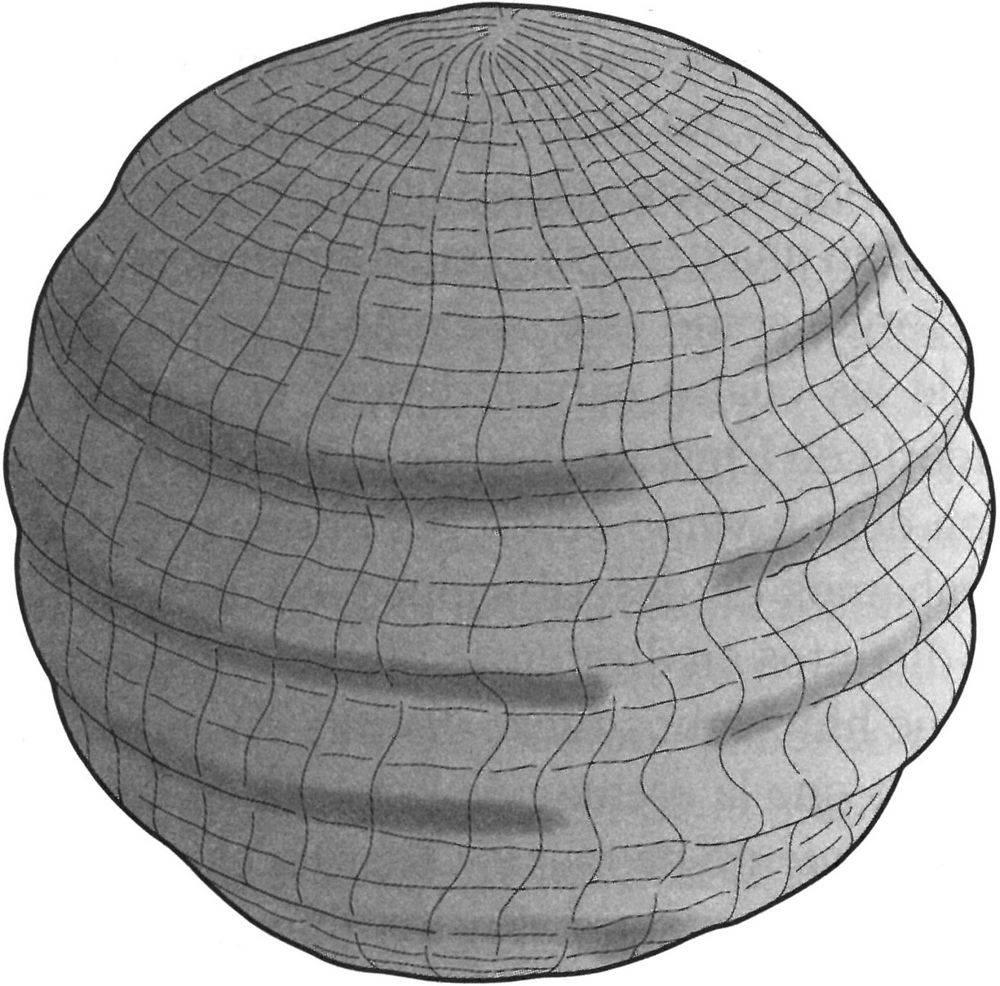
FIGURA 7.6. Un espacio con curvatura anisótropa se puede comportar como un universo abierto en algunas direcciones y como un universo cerrado en otras. Estas curvaturas direccionales pueden cambiar de positiva a negativa y viceversa con el paso del tiempo.

Estos nuevos universos con curvatura anisótropa tienen el mismo aspecto que los simples de curvatura isótropa, con la adición de ondas de energía gravitatoria. Las ondas se mueven en diferentes direcciones, con distintas intensidades, y su presencia crea una curvatura diferente en distintas direcciones a medida que se mueven. Que todos estos complicados eventos sucedan a la vez y, aun así, el universo siga teniendo el mismo aspecto desde cualquier lugar dentro de él es algo muy restrictivo, y por eso el número de posibilidades es limitado; en concreto, las nueve que descubrió Bianchi. Si se permite que las cosas sean distintas en cada punto, el número de universos posibles se convierte en infinito. El grupo de universos de Taub es como la restricción que un pintor impone a su creatividad al encerrarla en un marco, o como la de una escultora que opta por expresarse únicamente en piedra. La consecuencia de las restricciones autoimpuestas es fijar el centro de atención.

Universos suaves y una nueva ventana observacional

Siempre está oscuro. La luz se limita a ocultar la oscuridad.

Daniel McKiernan

En el último capítulo supimos acerca del notablemente casual descubrimiento de la radiación cósmica de fondo de microondas que quedaba como rastro de las primeras etapas del universo. La temperatura media que se dedujo para esta radiación fue de unos 2,7 grados Kelvin, pero los radioastrónomos de Princeton pronto se dieron cuenta de que podían efectuar un tipo de medida distinta con una precisión muy superior. Es muy difícil medir la temperatura con mucha precisión, porque se necesita una temperatura de referencia absoluta con la que comparar. Actualmente, las mejores mediciones de temperatura se llevan a cabo en el espacio, desde satélites, pero estos satélites tienen que transportar un frasco aislado de helio líquido a una temperatura próxima a los 2,7 grados Kelvin como referencia de comparación. Ese líquido acaba por evaporarse, lo que limita la duración posible del experimento.

En 1967, Dave Wilkinson y Bruce Partridge aprovecharon un ingenioso aparato electrónico inventado por Robert Dicke para medir las posibles diferencias de temperatura en diversas direcciones en el cielo con una precisión muy superior de la que era posible la temperatura media. La medición de las diferencias puede llevarse a cabo con mucha exactitud porque no exigen una medición de la temperatura. Wilkinson y Partridge buscaron cambios en la intensidad de la radiación de fondo y no hallaron ninguno hasta el nivel de sensibilidad de su detector, de modo que pudieron mostrar que las variaciones de temperatura de una dirección a otra eran inferiores al 0,1 por ciento: la radiación de fondo era extraordinariamente isótropa, y no había grandes acumulaciones de materia en el universo que distorsionasen su expansión de forma significativa^[239].

Este descubrimiento era muy sorprendente: mostraba que el universo se expandía con una extrema isotropía; tan grande, de hecho, que los cosmólogos empezaron a replantearse su actitud hacia el alto grado de simetría manifestado por el universo. Anteriormente, los cosmólogos habían asumido que el universo era prácticamente isótropo y homogéneo. El gran rompecabezas consistía en explicar el motivo de las pequeñas irregularidades sobre este telón de fondo suave, y cómo estas irregularidades crecían hasta convertirse en las galaxias y los cúmulos que vemos actualmente. Poco después de descubrir el alto nivel de isotropía de la radiación de fondo, los cosmólogos empezaron a considerar que los verdaderos misterios eran la suavidad de fondo y la expansión casi perfectamente isótropa. Después de todo, si eligiésemos universos al azar a partir de soluciones de las ecuaciones de Einstein o de la galería de espacios de Bianchi, sería mucho más probable elegir uno irregular que se expande anisotrópicamente que uno maravillosamente suave e isótropo. El número de formas en que un universo puede ser irregular es muy superior, así que ¿por qué nuestro universo es tan improbablemente suave y simétrico?

Universos caóticos

Todos los caminos llevan a Roma.

Jean de la Fontaine^[240]

Estimulado por las observaciones de la radiación de fondo de microondas tomadas en 1967, Charles Misner, de la Universidad de Maryland, propugnaba un enfoque completamente novedoso^[241]. En lugar de asumir que el universo es suave e isótropo, de modo que el orden procede solamente del orden, ¿por qué no intentar demostrar que el orden siempre será el resultado del caos?

La «cosmología caótica» de Misner intentaba mostrar que las ecuaciones del universo de Einstein tienen la propiedad de que, independientemente del caos con el que los universos inician su expansión, si se espera lo suficiente (y hasta ahora disponemos de 14 000 millones de años de historia disponibles) pasarán a ser suaves y cada vez más isótropos.

Se trata de una idea atractiva con implicaciones filosóficas de peso. Si es verdad, significa que no necesitamos saber cómo fue el principio del universo (ni siquiera si lo hubo) a fin de comprender su estructura actual. La idea de Misner era señalar que, si un universo empieza con un estado de expansión caótica, en sus primeras fases surgirán de forma inevitable fuentes de fricción que suavizarán las irregularidades y garantizarán que el universo acabe siempre expandiéndose de forma uniforme e isótropa. Es parecido a tomar un cubo de aceite y removerlo vigorosamente. Si se cierran los ojos no se verá el oleoso remolino que se crea, pero sabemos que, al cabo de un minuto, el aceite siempre tendrá el mismo aspecto: los movimientos se habrán amortiguado y su superficie será siempre suave y tranquila. ¿Podría suceder lo mismo con los universos?

Esta nueva cosmología caótica era muy ambiciosa. Hasta entonces, a los astrónomos les había bastado con hallar uno de los universos posibles de Einstein que describiese nuestras observaciones de la forma más precisa posible. Los candidatos más simples y simétricos funcionaban muy bien. Entonces, las observaciones de la radiación de fondo dieron relevancia al hecho de que, en realidad, no es que funcionasen: es que lo hacían asombrosamente bien. ¿Por qué? Esa fue la cuestión que planteó Misner. Algunos cosmólogos tenían suficiente con aceptar que el universo era actualmente muy simétrico porque había empezado así. «Las cosas son como son porque eran como eran», como dijo Tommy Gold en tono jocoso^[242]. Pero esto no era realmente una explicación, y Misner aspiraba a algo mejor. Si podía demostrar que la simetría actual surgía de cualesquiera condiciones iniciales (o aunque solo fuera de la mayoría de ellas), habría llegado a una explicación satisfactoria de la estructura del universo.

Al principio, el enfoque Misner parecía bastante prometedor. Los universos anisótropos más simples basados en los tipos de espacio hallados por Bianchi, Kasner y Taub tendían, en efecto, a hacerse cada vez más isótropos a medida que avanzaba la expansión. Por desgracia, las posibilidades más complicadas —y también más probables— no compartían esta bonita propiedad. No se podía confiar en que la expansión del universo hiciese que las irregularidades fuesen cada vez menos significativas. En algunos universos no se amortiguan en absoluto a menos que surja algún proceso físico específico que las reduzca más rápido de lo que el universo se expande. El desafío consistía en hallar estos «procesos suavizadores».

Por desgracia, se demostró que se trataba de una empresa imposible. Richard Matzner, de la Universidad de Texas-Austin, y yo mismo señalamos que la propia radiación de fondo nos indicaba que en el pasado apenas podían haberse limado irregularidades^[243]. Toda disipación de irregularidades por fricción genera calor —que es donde acaba la energía de la irregularidad, gracias a la segunda ley de la termodinámica—, y la radiación de fondo es donde se encuentra el calor actualmente. Cuanto más pronto operan los procesos de fricción, más calor producen. La cantidad total de calor que contiene actualmente el universo —alrededor de mil millones de fotones por átomo— resulta un límite realmente restrictivo a la cantidad de irregularidad que puede haber quedado amortiguada y erradicada en el pasado. De hecho, solo una mínima cantidad de irregularidad podría haberse disipado en las primeras etapas de la historia del universo: no era posible que los universos que empezaban en un estado muy irregular se suavizaran hasta llegar a la bonita expansión isótropa que vemos en la actualidad sin generar una cantidad imposible de radiación térmica. Misner destacó también una característica singular de todos los universos estudiados hasta entonces, tanto los altamente simétricos como los que no. La luz viaja a una velocidad finita y define un límite cósmico de velocidad para la actuación de cualquier tipo de señal o de proceso de fricción. Cuando la edad del universo es de t segundos, solo ha habido tiempo para que la luz recorra una distancia «horizonte» de alrededor de 10⁵ × t kilómetros, y esto contiene una masa igual a 100 000 × t veces la masa del Sol; así que, al cabo de 10 segundos, solo puede haber viajado un millón de kilómetros (la distancia de la Tierra al Sol es de 150 millones de kilómetros) y afectado a una masa de un millón de veces la del Sol. Y sin embargo, observamos uniformidad en el universo hasta dimensiones 10¹⁵ veces mayores.

Esta conclusión proyecta además una gigantesca sombra sobre la filosofía de la cosmología caótica. Cualquier proceso capaz de amortiguar las diferencias de temperatura, densidad y ritmo de expansión de un lugar a otro en las primeras fases del universo está limitado a escalas muy reducidas que no pueden explicar por qué el universo, a gran escala, es tan similar de un lugar a otro, y por qué la temperatura de la radiación de fondo es tan similar en todo el cielo.

Si nos fijamos en distintos puntos del cielo separados por más de dos grados y que tienen la misma temperatura hasta un alto grado de precisión, no hubo tiempo para que las señales lumínicas viajasen de uno a otro y compensasen las diferencias en energía y temperatura antes de que los fotones empezasen a viajar libremente hacia nosotros cuando el universo tenía una edad de unos 250 000 años. Nuestras observaciones de la radiación de fondo son como fotografías de ese momento.

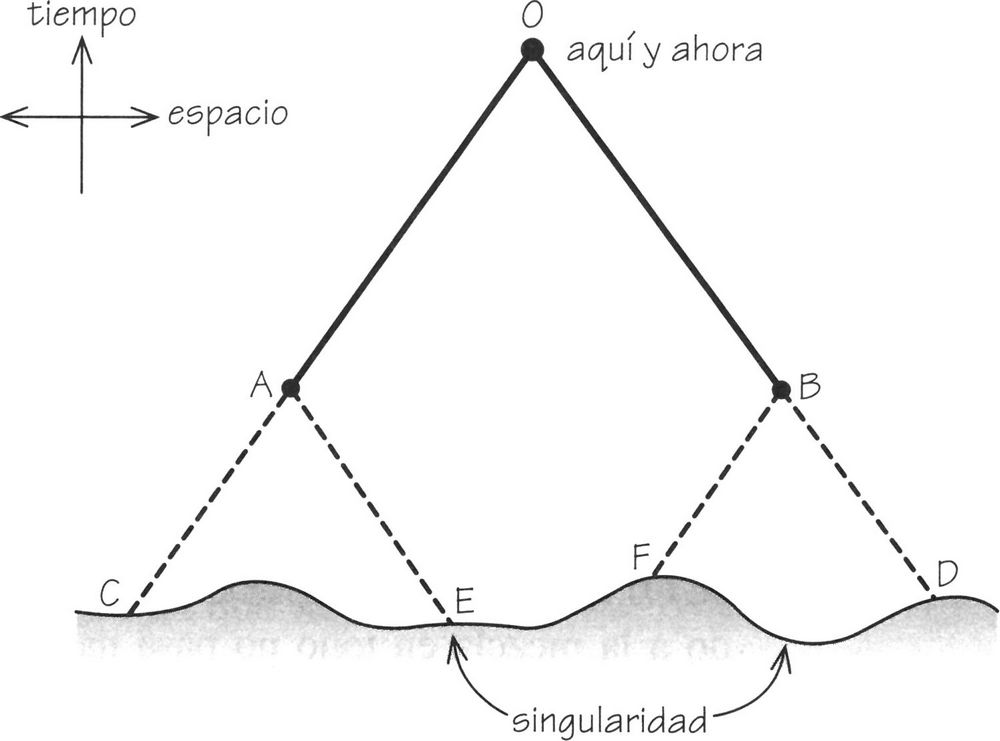
FIGURA 7.7. Los rayos de luz viajan hacia nosotros a través del espacio y el tiempo por un «cono de luz», como se muestra en el diagrama. El cono define nuestro horizonte visual. Las partes del universo fuera de este cono de luz OCD son inaccesibles a nosotros desde el punto de vista de la observación. Tomemos dos puntos (A y B) en nuestro cono de luz en el pasado, donde los fotones de la radiación de fondo de microondas empezaron a viajar libremente hacia nosotros, cuando el universo tenía solo unos pocos millones de años. Podemos hallar los conos de luz del pasado (ACE y BFD) correspondientes a estos puntos. No se intersecan durante toda la historia pasada del universo, hasta su principio. Eso significa que ninguna señal luminosa ha tenido tiempo de pasar entre A y B durante la historia del universo: las condiciones en A y en B no pueden estar coordinadas por procesos físicos que se muevan a la velocidad de la luz. Y sin embargo, se halla que la temperatura y la densidad en A y en B son iguales hasta una precisión de una milésima del uno por ciento.

Esta simple deducción se traduce en que, o bien es necesario imaginar una «nueva física» que pueda evitar el límite cósmico de velocidad para el proceso de «suavizado», o bien una condición inicial especial para el universo que descarte los universos exóticos e irregulares como descripciones del cosmos real.

Universos mixmaster

La mezcla armónica es una técnica avanzada utilizada por los mejores DJ del mundo […] Obviamente, aprender a mezclar en tono es una técnica de DJ avanzada; si tu aprendizaje aún no ha llegado a la mezcla en tono no pasa nada, pero hazte una nota mental: la mezcla en tono es una fase futura que vas a necesitar si quieres convertirte en un DJ de categoría mundial.

The DJ Master Course^[244]

En 1969, Misner respondió a las limitaciones del ámbito de la disipación en las primeras etapas del universo al encontrar un nuevo tipo de solución para las ecuaciones de Einstein^[245]. Su espacio tenía una de las formas más complicadas de las halladas por Bianchi, y su volumen era finito. Se trataba de un universo «cerrado» que se iniciaba con un big bang, llegaba a un máximo de expansión y a continuación se contraía en un big crunch. Sin embargo, la forma de su expansión era tan complicada que no era en absoluto posible resolver las ecuaciones de Einstein, aunque se podía hacer un esquema general de su comportamiento y estudiar partes de él en un ordenador. Más adelante se llegó a la conclusión de que su comportamiento es caóticamente impredecible^[246], una propiedad que se convirtió en un área de interés clave para la ciencia a finales de la década de 1970.

Misner denominó a su nuevo tipo de universo «Mixmaster», por la marca de una batidora de alimentos que se vendía en Estados Unidos^[247], porque creía que su geometría retorcida y rápidamente cambiante podía permitir que la luz recorriese el universo y le diese homogeneidad. Por desgracia, estudios detallados revelaron que, aunque la luz podía recorrer una gran distancia dentro de un universo Mixmaster, se trataba de un caso excepcional y la mezcla era generalmente ineficaz.

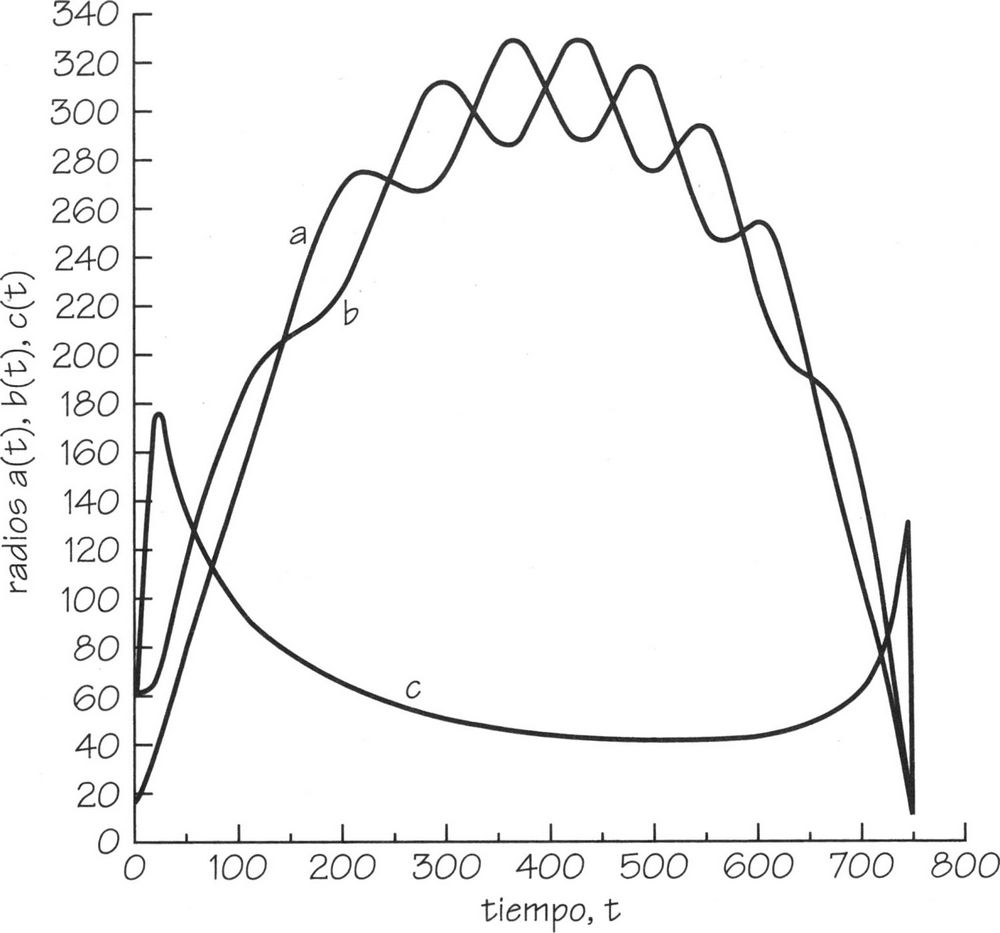
FIGURA 7.8. Oscilaciones Mixmaster. Durante la primera mitad de la vida del universo, su volumen aumenta y dos direcciones se expanden, mientras que la tercera se contrae. Durante la segunda mitad, el volumen total se reduce a cero al acercarse al big bang. Las direcciones de expansión y contracción se intercambian de forma caótica y aleatoria, como el temblor de un postre de gelatina, con períodos en los que dos direcciones oscilan mientras la tercera cambia de forma estable, seguidos por períodos en los que uno de los ejes oscilantes se cambia por el eje que cambia de forma estable. Aquí solo se muestran algunas de las infinitas oscilaciones. Los radios en las tres direcciones perpendiculares son a(t), b(t) y c(t).

El universo Mixmaster era el más complicado de los universos de Einstein que se había visto (Figura 7.8). Al efectuar su seguimiento hacia el principio, sufría un número infinito de oscilaciones. En cualquier instante, dos direcciones se expanden y una se contrae, como en el universo de Kasner. No obstante, la dirección de contracción se ve permutada una y otra vez aleatoriamente y, a medida que nos acercamos al principio, nos encontramos con un número infinito de permutaciones de las direcciones de expansión y contracción. Es algo parecido a una gelatina que tiembla^[248].

Las razones de esta complejidad están relacionadas con la imagen de la gravedad de Einstein: en la antigua teoría gravitatoria de Newton no existe un homólogo para un universo como este. Se empieza con un universo que se expande a ritmos distintos en direcciones diferentes y luego se introducen ondas gravitatorias en cada una de ellas que rizan el espacio en diferentes direcciones, al tiempo que curvan el espacio en el que se mueven. La onda que se mueve en la dirección de la implosión crea una gran curvatura que acaba por hacer retroceder a la onda, y la implosión se invierte en una expansión, y una de las otras direcciones pasa a implotar. La secuencia de cambios repite con una frecuencia infinita al seguirla hacia atrás hasta el principio.

Este estado de cosas es realmente extraño, y está relacionado con una pregunta filosófica muy antigua planteada por Zenón de Elea en el siglo V a. C.: ¿se puede hacer un número infinito de cosas en un tiempo finito? A Zenón le gustaba desafiar a otros filósofos con paradojas maravillosamente bien planteadas sobre el infinito, que nunca obtuvieron respuesta en su época. Por ejemplo, si la distancia entre tú y la puerta es de 1 metro, para alcanzar la puerta deberás avanzar primero ¹⁄₂ metro, luego ¹⁄₄ de metro, luego ¹⁄₈ de metro, a continuación ¹⁄₁₆, etc., para siempre. La distancia total de este número infinito de pasos^[249] es igual a 1 pero, mantiene Zenón, deberás dar un número infinito de pasos para alcanzar la puerta, y nunca llegarás a ella.

El universo Mixmaster efectúa un número infinito de oscilaciones físicamente diferenciadas en una cantidad finita del mismo tiempo que podemos medir con un reloj. Misner sostenía que, si se rechazaba la paradoja de Zenón porque un número infinito de subdivisiones de la distancia de uno mismo a la puerta no son eventos físicos diferenciados, se debe concluir que el universo Mixmaster es infinitamente viejo, porque en él tienen lugar un número infinito de oscilaciones físicamente diferenciadas antes de alcanzar t = 0^[250].

Físicamente, esto es algo muy extraño. Los matemáticos, en cambio, están acostumbrados a cosas así: el gráfico de y = x²sin(1/x), si pudiera dibujarse (para lo que se necesitaría un lápiz infinitamente fino), contendría un número infinito de oscilaciones en cualquier intervalo de x, por pequeño que fuese, que contuviera el valor x = 0 (Figura 7.9).

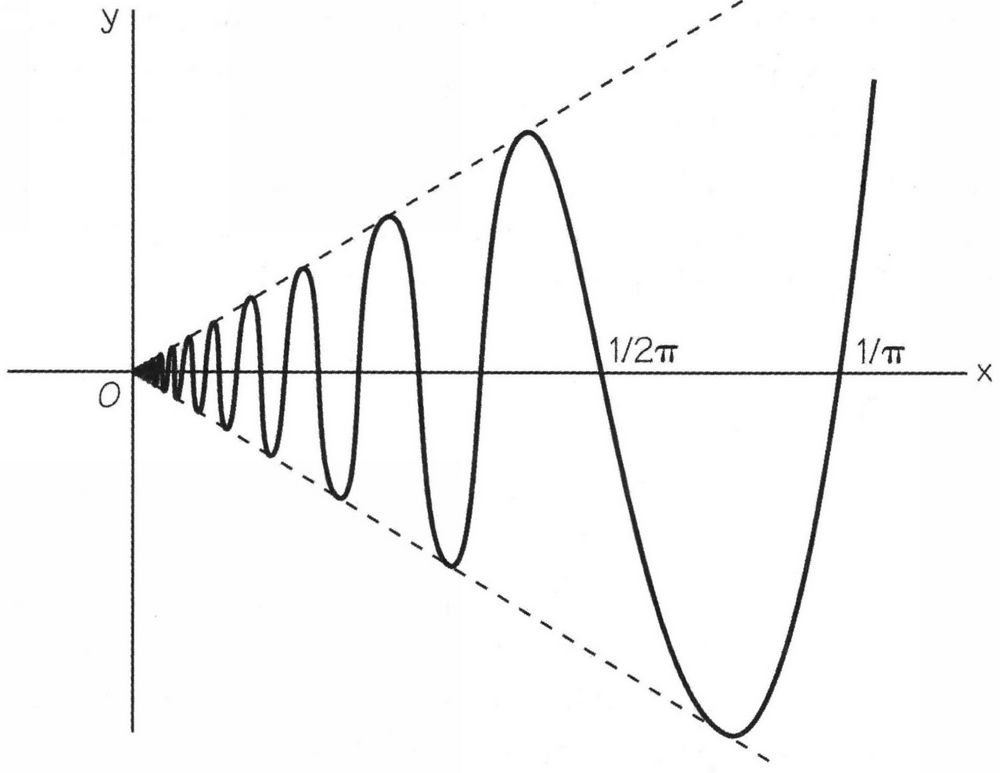
Figura 7.9. La gráfica de y = x²sin(1/x). Esta gráfica experimenta un número infinito de oscilaciones al acercarse a x= 0. Solo podemos trazar algunas de ellas.

A los cosmólogos les inquieta tomarse de una forma demasiado literal lo del «principio» a t = 0. Se espera que la teoría cuántica empiece a afectar fuertemente a todo el universo cuando este tiene una edad inferior a 10⁻⁴³ segundos. Este es el punto en el tiempo más temprano en el que las oscilaciones Mixmaster pueden tener un sentido físico. Pero el universo se expande tan rápidamente en comparación con la frecuencia de las oscilaciones que, incluso aunque estas continuasen hasta el presente, solo habría habido tiempo para que sucediesen alrededor de una docena de ellas. En un universo realista, el número de oscilaciones queda muy lejos del número infinito necesario para que la luz viajase repetidamente a grandes distancias al principio. Casi todas las oscilaciones tienen lugar en la proximidad inmediata de t = 0, como ilustra la Figura 7.9. Esta infinitud está muy «ocupada» cerca del principio.

A pesar de la decepción de saber que el universo Mixmaster no era la clave para comprender la estructura actual del universo, ha seguido estando en el centro del interés, ya que sigue representando el comportamiento más general y complicado jamás hallado en soluciones a las ecuaciones de Einstein, y sigue siendo un desafío intentar demostrar si puede tratarse del tipo de universo más general que permiten esas ecuaciones.

Lamentablemente, llegado el año 1980 los argumentos de este tipo habían convencido a los cosmólogos de que la atractiva idea de mostrar que los procesos físicos en los primeros momentos de la historia del universo garantizarían siempre que la expansión iba a ser isótropa no se sostenía. Había demasiados tipos de irregularidades persistentes de las que librarse, y cualquier proceso que se encargase de suavizarlas sufría graves limitaciones en su ámbito debido a la finita velocidad de la luz y a la cantidad de entropía de radiación actual en el universo.

Universos magnéticos

Examen oral de Ciencias Naturales en la Universidad de Oxford, c. 1890^[251]

El súbito interés por los universos que se expandían a ritmos distintos en diferentes direcciones llevó a los cosmólogos a pensar acerca de los tipos de energía que solo podrían existir en ese tipo de universos. Anteriormente, su atención se concentraba por entero en posibilidades muy simples: la radiación del cuerpo negro y lo que llamaban «polvo», un gas de galaxias o estrellas que no ejerce presión (porque las galaxias y las estrellas no se encuentran con frecuencia entre sí). Pero estas no son las únicas energías y masas en el universo. Y uno de los mayores y más antiguos misterios ha sido la presencia del magnetismo.

Los campos magnéticos son ubicuos en el universo. Están en los planetas, las estrellas y las galaxias. ¿De dónde vienen? ¿Posee el universo un campo magnético que lo invade todo, del que estos campos más pequeños derivan en última instancia? Una posibilidad digna de ser tenida en cuenta es que los campos surgieron al principio del universo y se extendieron y debilitaron debido a la expansión, junto con toda la materia y radiación. Más adelante, la fuerza de la gravedad los habría atraído a las galaxias, donde se habrían amplificado rápidamente por la rotación para producir los campos magnéticos más intensos que vemos actualmente entre estrellas y en las propias estrellas. Aún no sabemos si el origen de los campos magnéticos es así de simple o si fueron producidos, de forma casi aleatoria, por algún complicado proceso en un momento definido de la historia inicial del universo.

Si los campos magnéticos ya estaban presentes desde el mismo principio, esto exige que el universo se expandiese a ritmos distintos en direcciones diferentes para sostener las presiones y tensiones anisótropas que ejerce un campo magnético cósmico universal. Entre 1965 y 1967, el astrofísico norteamericano Kip Thorne y los cosmólogos rusos Ya Zeldovich y Andre Doroshkevich hallaron nuevas soluciones a las ecuaciones de Einstein que describían universos anisótropos que contenían materia o radiación ordinarias junto con un campo magnético cósmico. Estas soluciones confirmaban la necesidad de un principio altamente anisótropo, pero también revelaban que el efecto del campo magnético en la posterior evolución del universo es bastante extraño: hace espectacularmente más lenta la disminución de cualquier anisotropía, y deja una huella característica en la radiación de fondo de microondas si su intensidad es demasiado alta. La ausencia de esta propiedad de la radiación de fondo ha permitido a los cosmólogos poner unos límites muy estrictos a la intensidad de este campo magnético universal^[252].

Los universos de Brans y Dicke

No te creas ningún resultado experimental hasta que la teoría no lo prediga.

Anónimo

Durante la década de 1960 empezaron a surgir dudas sobre si, después de todo, la teoría general de la relatividad de Einstein era correcta. Las observaciones de la órbita del planeta Mercurio eran diferentes de lo predicho por Einstein en un nivel preocupante. Este problema se acabó resolviendo a partir de una mejor comprensión de la actividad turbulenta en la superficie del Sol —y, por lo tanto, de su verdadera forma y diámetro—, pero hasta entonces el problema parecía grave. Dicke había sido uno de los pioneros de nuevos métodos para comprobar teorías gravitatorias utilizando datos geológicos y paleontológicos junto con la astronomía, y en 1966 había efectuado mediciones de la forma del Sol que representaban un problema para la relatividad general. Las dificultades no quedaron totalmente resueltas mediante otras observaciones hasta 1973^[253].

Recordando los antiguos trabajos de Dirac sobre grandes números, y la posibilidad de que la «constante» de gravitación de Newton, G, no fuese constante, en 1961 Dicke y su asistente de investigación Carl Brans desarrollaron una impresionante generalización de la teoría de Einstein^[254] (Figura 7.10a) en la que ascendían la constante de gravitación a la categoría de magnitud que, como la densidad o la temperatura, podía variar en el espacio y en el tiempo. Si esto se hace de la forma correcta, y no simplemente convirtiendo G en una variable en las ecuaciones en las que no varía —como hizo Dirac—, el resultado es una nueva teoría con fuertes restricciones. Las variaciones no son arbitrarias: deben conservar la energía y el momento y, como el resto de formas de energía, curvarán el espacio y afectarán al flujo del tiempo. Si G se convierte en constante, la teoría de Brans y Dicke se convierte simplemente en la teoría de Einstein. Pero si se permitía una variación muy lenta, la teoría de Brans y Dicke implicaba cambios en el movimiento del planeta Mercurio, lo que daba explicación a las observaciones (¡que más tarde se demostró que no se habían interpretado correctamente!).

Los universos de Brans y Dicke eran muy similares a los de la teoría de Einstein. Algunos se expandían siempre, otros llegaban a un tamaño máximo y se contraían; pero había pequeñas diferencias. La constante de gravitación podía disminuir mucho más lentamente que en el escenario original de Dirac. Si G disminuía con el tiempo como 1/tⁿ, la expansión del universo crecía en escala como t^(2−n)/3, de modo que, cuando n era cero y G no variaba con el tiempo, teníamos el universo simple de Einstein y De Sitter, cuya escala crece^[255] como t^2/3 (Figura 7.10a).

Diversos estudios de datos astronómicos y pruebas de gravedad en el sistema solar revelaron que las predicciones de Einstein para el movimiento de Mercurio eran exactas, y el valor de n se aproximaba cada vez más a cero. Llegado el año 1976, el interés por estas teorías había menguado, pero veinticinco años más tarde, volvieron a aparecer como guía fundamental para crear generalizaciones de la teoría de Einstein en las que otras constantes tradicionales de la Naturaleza podían variar y quedar descritas de forma coherente.

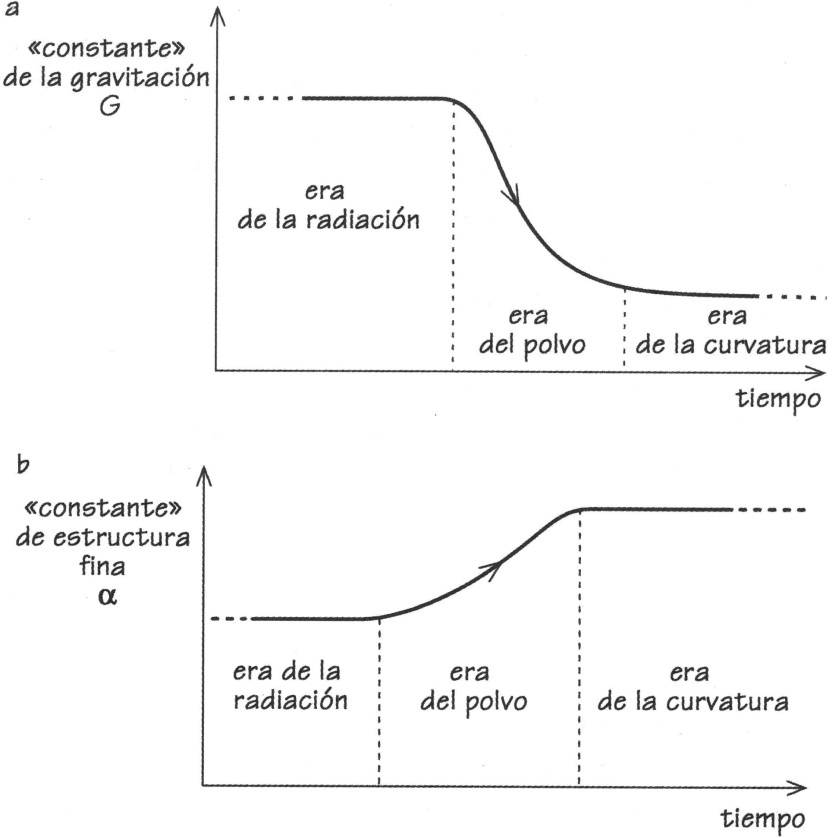
Figura 7.10. (a) Comportamiento típico de una «constante» gravitatoria variable, G, a lo largo de la edad del universo en cosmologías predichas por la teoría gravitatoria de Carl Brans y Robert Dicke. El valor de G solo cambia de forma significativa cuando la materia sin presión («polvo») domina la densidad del universo. Los cambios se detienen en la era dominada por la radiación, o cuando la curvatura domina un universo abierto, (b) El cambio esperado en el valor de una constante de estructura fina, α, variable con el tiempo, en la teoría cosmológica de Sandvik, Barrow y Magueijo. No hay cambios durante las fases de la historia cósmica dominadas por la radiación o la curvatura. Durante la era del polvo, α debería crecer muy lentamente, en proporción al logaritmo de la edad del universo.

A partir de 1999 se empezó a acumular una cantidad impresionante de datos astronómicos procedentes de los espectros de la luz de quasars, que indicaban que una combinación de las constantes de la Naturaleza (como la carga eléctrica de un electrón, su masa o la velocidad de la luz) que gobiernan la física en el nivel del átomo podrían haber sido ligeramente distintas hace 10 000 millones de años^[256]. Estas observaciones son coherentes con un aumento muy lento en el valor de una combinación de constantes de la Naturaleza denominada «constante de estructura fina^[257]» a lo largo de la historia cósmica reciente, a un ritmo un millón de veces más lento que el ritmo de expansión del universo. La novedad de estas observaciones sobre los quasars, y el motivo de que las obtuviéramos por primera vez en 1999, se debía a que eran más sensibles a los cambios en la constante de estructura fina que cualquier experimento de laboratorio.

Estas observaciones requerían una generalización de la teoría de la gravedad de Einstein que pudiese incluir, sin perder su propia coherencia, variaciones en la constante de estructura fina, que controla la intensidad de la electricidad y del magnetismo. Jacob Bekenstein^[258], Håvard Sandvik, João Magueijo y yo mismo^[259] hallamos en 2002 una teoría análoga a la de Brans y Dicke que ofrece una predicción simple del cambio de la constante a lo largo del tiempo (Figura 7.10b). La electricidad y el magnetismo no tienen ningún papel significativo a escalas astronómicas, de modo que esta teoría no produce cambios medibles en la expansión del universo, aunque la expansión determina el lento crecimiento de la «constante» a lo largo del tiempo.

Universos de materia-antimateria

Oh dear, what can the matter be?

Canción infantil inglesa^[260]

El descubrimiento de la radiación de fondo de microondas en 1965 generó un repentino interés por los universos de big bang, y el abandono de alternativas tradicionales, como el modelo de estado estacionario. Los argumentos dominantes sobre «en qué clase de universo» vivimos se centraban en si el universo caliente de los primeros tiempos era isótropo, anisótropo o incluso totalmente caótico. Sin embargo, aún había personas a quienes disgustaba profundamente la imagen del big bang, o que conservaban una inclinación filosófica por el modelo de estado estacionario porque no tenía principio ni final: era el universo más simétrico posible porque lo era tanto en el tiempo como en el espacio. Había también otros que rechazaban tanto el modelo de big bang como el del estado estacionario y buscaban imágenes bastante diferentes de lo que podía haber sucedido en la historia más temprana del universo en expansión. Una interesante teoría de este tipo fue motivada por el papel de la antimateria en el universo.

Paul Dirac predijo en 1928 la necesidad de la existencia de antimateria^[261] en la Naturaleza, y en 1932 Carl Anderson la descubrió por primera vez —en forma de antielectrones («positrones») procedentes del espacio—; más adelante, en 1955, Owen Chamberlain, Emilio Segre, Clyde Wiegand y Tom Ypsilantis generaron e identificaron antiprotones en la Universidad de California-Berkeley.

Pronto, la trascendencia cósmica de la antimateria se convirtió en un tema de debate. A mediados de la década de 1960, dos destacados físicos suecos, Hannes Alfvén y Oskar Klein, sugirieron que el universo empezó con cantidades iguales de materia y antimateria en un estado muy extenso y de baja densidad, la situación opuesta al big bang. La materia y la antimateria se atraerían poco a poco entre sí por efecto de la gravedad y, finalmente, las partículas empezarían a colisionar con las antipartículas, aniquilándose y generando cantidades colosales de radiación. Esta explosión detendría la convergencia de partículas y antipartículas, impulsándolas de nuevo hacia fuera en un estado de expansión. Este proceso podría no suceder en todas partes, pero ellos sostenían que correspondía a la expansión que veíamos actualmente, porque necesariamente nos hallamos en una de las regiones en las que la aniquilación de partículas con antipartículas ha detenido la contracción y la ha convertido en expansión.

Alfvén no era cosmólogo, sino especialista en física del plasma y en campos magnéticos, y había obtenido el premio Nobel de Física por esos trabajos en 1970. La cosmología de materia-antimateria de Alfvén no atrajo demasiada atención y pronto se demostró que contradecía diversas observaciones^[262]. Exigía una simetría global materia-antimateria en el universo: por cada átomo tenía que existir un antiátomo, y una antiestrella por cada estrella. No podíamos ver estos antiátomos, antiplanetas y antiestrellas, de manera que la aniquilación debía haber provocado regiones del espacio muy separadas para toda la materia y la antimateria; pero ¿cómo? Y lo que es peor: la inversión de la contracción para pasar a expansión habría tenido lugar cuando la densidad del universo era 100 veces menor de la que vemos actualmente. Este tipo de «rebote cósmico» no podía haber sucedido en nuestro pasado.

Otras personas con conocimientos más profundos sobre física de altas energías, como Roland Omnes, intentaron desarrollar a finales de la década de 1960 una teoría del universo de materia-antimateria en el contexto de un universo de big bang. De nuevo, la hipótesis inicial era que el universo contenía la misma cantidad de materia que de antimateria y que esta simetría se conservaba; en aquel momento se consideraba que la inmutabilidad del equilibrio global de materia-antimateria era una ley inviolable de la Naturaleza^[263]. Para poder conciliar esta ley con la ausencia de pruebas de la existencia de antimateria en nuestro universo próximo era necesario que hubiera islas independientes compuestas íntegramente de materia o de antimateria en el universo.

Lamentablemente, si retrocedemos en el tiempo en el proceso de expansión del universo, estas islas acaban chocando entre sí. Debían haber empezado todas mezcladas junto con la radiación en un estado de equilibrio, con partículas y antipartículas apareciendo y desapareciendo en el mar de radiación durante el primer milisegundo de la historia del universo. Era posible calcular lo que sucedía cuando cantidades iguales de materia y de antimateria, distribuidas democráticamente, dejaban de aniquilarse entre sí. Por desgracia para esta teoría, el proceso de aniquilación es muy eficiente, y Zeldovich y Hong-Yee Chiu mostraron en 1965 que solo puede sobrevivir un protón o un antiprotón por cada 10¹⁸ fotones^[264]. Lo que vemos en el universo actualmente es un promedio de 10⁹ fotones por cada protón. Nuestro universo contiene, de lejos, demasiados protones y átomos y demasiada poca radiación térmica como para haber surgido de mundos con cantidades iguales de materia y antimateria en colisión.

La antimateria estaba fuera del menú cosmológico. Pero las cosas pronto iban a cambiar. En la década de 1970 iba a tener lugar una revolución en la cosmología que volvía a poner la disciplina en el centro de atención, y que dio paso a la mayor de las sorpresas sobre nuestra concepción del universo.