3 

Los universos de Einstein

Einstein me explicó su teoría cada día; cuando llegué, estaba totalmente convencido de que él la había entendido.

Chaim Weizmann, acompañante de Einstein en un viaje transatlántico a Nueva York en 1921^[71].

Completando una visión copernicana

Me he dado cuenta de una paradoja en la cultura de los abogados del gobierno: cuanto menos segura es una ley, más seguras son sus visiones.

Jack Straw^[72]

Todas las imágenes del universo esbozadas por los astrónomos del siglo XIX utilizaban la guía de estilo que Newton ofreció por primera vez en 1687. Sus famosas leyes del movimiento y de la gravedad son útiles para todo tipo de finalidades prácticas (construir puentes, probar coches, guiar aviones, lanzar piedras), pero si se examinan más de cerca, un problema acecha en las profundidades. Por desgracia, solo son válidas para un tipo de observador muy especial, un observador que no rota ni acelera con relación a las estrellas más distantes. Como vimos en la página 41, si se mira por la ventana de un cohete en rotación (Figura 3.1) se ven estrellas acelerando, aunque ninguna fuerza actúe sobre ellas.

Einstein veía en esto un grave problema sobre la forma en que estábamos formulando nuestras leyes de la Naturaleza. Para él era intolerable que tuviésemos una descripción de las leyes naturales que fuese selectiva con un conjunto especial de observadores para los cuales, en virtud de su movimiento, el mundo tenía un aspecto más simple: esto equivalía a decir que algunas personas poseían un conocimiento revelado especial que no está a disposición de todos los demás. En esencia, se trataba de una visión del mundo precopernicana en la que nuestro movimiento, no nuestra posición, poseía un estatus especial en el universo.

FIGURA 3.1. Si miran por las ventanas de una nave en rotación, los astronautas ven las estrellas pasar aceleradas, pero no pueden ver fuerzas que actúen sobre ellas.

Uno de los grandes logros de Einstein fue encontrar una forma de hallar y formular leyes de la Naturaleza que garantizasen que todos los observadores viesen las mismas leyes, sin importar cómo se moviesen. Su nueva ley de la gravedad, que sustituye la de Newton, se denomina teoría de la relatividad general, y muchas personas piensan que se trata de la más notable creación de la mente humana. Amplía la perspectiva copernicana de simplemente dictar que nuestra posición en el universo no debe ser privilegiada a exigir que cualquier físico, esté donde esté o se mueva como se mueva, halle las mismas leyes de la Naturaleza. ¿Qué significa esto en la práctica?

Supongamos que miramos hacia el cielo y observamos que, cuando sucede A, siempre produce el resultado B. Hemos detectado así una ley de la Naturaleza que denotamos mediante la ecuación A = B. Vamos a poner ahora todo el instrumental de medida en una nave espacial y a lanzarla al espacio. La nave puede girar o acelerar según un esquema muy complicado. Al efectuar cuidadosas observaciones de A, siempre tiene un aspecto distinto a causa de los efectos del movimiento y, en lugar de medir A, como sucedía en el suelo, la medida es A*. Del mismo modo, en lugar de tener el efecto B, el resultado es siempre B*, que es simplemente el valor de B teniendo en cuenta el nuevo movimiento con relación al suelo. La formulación de Einstein garantiza que la ley de la Naturaleza que se halle será de la forma A* = B*, sea cual sea el movimiento de la nave espacial. Las A y las B tienen valores diferentes, pero la forma de la ley que las relaciona, sea A = B o A* = B*, tiene la misma forma en la nave que en el suelo. Las leyes de Newton no eran así. La ley A = B hallada en una nave espacial que no girase se convertiría en una ley mucho más complicada si se observasen los mismos eventos desde una nave en rotación:

A* = B* + (algo adicional)

Para Einstein, una perspectiva copernicana completa se debía aplicar al mundo de las leyes de la Naturaleza, no solo a sus resultados: los planetas, las estrellas y las galaxias.

La inspiración de Einstein

Había que reinventar el Universo, y los principios de Einstein eran como pequeñas lámparas que iluminaban su camino. Él fue capaz de delinear una teoría de la gravitación en la que todas las masas, todas las partículas, toda la energía del universo contribuía a su estructura: el espacio-tiempo se curvaba bajo el peso de la materia-energía.

Jean Eisenstaedt^[73]

En 1931, en Estados Unidos, Einstein asistió al estreno de la película muda Luces de la ciudad en compañía de su protagonista, Charlie Chaplin. La multitud vitoreó a las dos dispares celebridades, y se dice que Chaplin le comentó a Einstein: «A mí me aclaman porque todos me entienden, y a ti te aclaman porque nadie te entiende».

La teoría de la relatividad general de Einstein se ha convertido en sinónimo de ininteligibilidad y dificultad de comprensión: el desafío intelectual definitivo. Es cierto que el lenguaje matemático que Einstein utilizó para lograr la expresión copernicana de sus nuevas leyes del movimiento y la gravedad había sido un reto al principio, incluso para él. Hasta confesó que no era tan fuerte en matemáticas como necesitaba ser. Su talento especial era para la comprensión física, no para la hechicería matemática. Pero si él no podía con algún problema matemático, solía conocer a alguien que sí podía. Su amigo y antiguo alumno Marcel Grossmann era un matemático de talento, que se encontraba cómodo en las ramas más abstractas de la matemática moderna. Grossmann había reconocido también el notable talento de Einstein para examinar el núcleo del funcionamiento de la naturaleza, y lo ayudaba con entusiasmo siempre que le era posible. En 1912, Einstein aceptó una plaza de profesor en Zúrich, prefiriéndola a ofertas de otras universidades más prestigiosas, a fin de poder seguir trabajando en estrecha colaboración con Grossmann, que era profesor de matemática pura allí.

FIGURA 3.2. Marcel Grossmann (izquierda), con Albert Einstein, Gustav Geissler y Eugen Grossmann, cuando eran estudiantes en Zúrich.

Grossmann inició a Einstein a las nuevas matemáticas que necesitaba para expresar su visión de cómo la gravedad daba forma al universo. Le mostró que su deseo de hallar una manera «democrática» de escribir las leyes de la Naturaleza para que tuviesen el mismo aspecto para todos se podía lograr escribiéndolas en el lenguaje de una esotérica rama de la matemática, denominada cálculo tensorial, que garantizaba la universalidad que ansiaba. Grossmann también inició a Einstein en los profundos desarrollos que se habían producido en nuestra comprensión de la geometría de las superficies curvas complejas que Schwarzschild había empezado a explorar algunos años antes. Pero ¿para qué necesitaba Einstein conocer esa estrambótica geometría?

La imagen de Newton del espacio era la de un escenario fijo en el que se representaban los movimientos de objetos como planetas y cometas. Esas cosas iban y venían, pero el espacio era fijo, inmutado e inmutable, independientemente de la materia y de los movimientos que habitasen en su tejido. El espacio de Einstein era mucho más maleable. Como si fuese una gran lámina de goma, era deformado y configurado por la materia y el movimiento que se producían en él. En lugares en los que había una gran concentración de masa, la curvatura del espacio sería muy pronunciada. Lejos de cualquier masa, el espacio sería cada vez más plano y sin distorsión. Cuando un cuerpo se movía entre dos puntos, tomaría la ruta más rápida posible en la superficie curvada, es decir, la línea más recta sobre ella. En la vecindad de una gran masa, la geometría mostraría un socavón significativo, y un objeto que pasase tomando la ruta más rápida parecería ser atraído hacia el centro del socavón. Después de pasar, la dirección de su ruta quedaría desviada por la forma del espacio. Así, Einstein podía atribuir las fuerzas gravitatorias simplemente a la curvatura del espacio. Las fuerzas no eran necesarias en absoluto, bastaba con el espacio curvado.

Sin embargo, al principio, esto no suena más que a otra forma de decir que sí hay fuerzas. Pero en realidad hay algo más. En la antigua imagen de Newton con el espacio fijo, se podía imaginar una pelota girando en el escenario fijo del espacio. No tendría efecto alguno sobre alguien que se limitase a estar de pie en el escenario en las proximidades. En el esquema de Einstein, las cosas eran muy distintas. Si el espacio se comporta como una lámina de goma deformable, al hacer girar la pelota el espacio se retorcerá a su alrededor y, si estás de pie en las cercanías, notarás un tirón en la misma dirección de la rotación^[74]. Se trata de una verdadera diferencia.

Lo que Einstein tenía que hacer para convertir esta visión en una nueva teoría de la gravedad era hallar algunas ecuaciones especiales, las nuevas leyes de la gravedad, que nos dijesen cómo sería la forma del espacio y el flujo del tiempo para cualquier patrón de masa y energía, en reposo o en movimiento. Las ecuaciones nos dirían también cómo podían cambiar estos patrones para garantizar la conservación de cantidades como la energía. El físico norteamericano John Wheeler condensó la teoría de Einstein en dos frases: «La materia le dice al espacio cómo curvarse. El espacio le dicta a la materia cómo moverse».

Einstein escribió estas ecuaciones en el nuevo lenguaje matemático del cálculo tensorial en el que Grossmann le había iniciado. Esto garantizaba que las ecuaciones tenían exactamente el mismo aspecto para todos los observadores, se moviesen como se moviesen, rotando, acelerando, saltando o rizando el rizo. Fuera cual fuese el movimiento de sus laboratorios, deducirían las mismas leyes de la gravitación^[75].

Las ecuaciones de Einstein poseían la hermosa propiedad de que un teorema puramente matemático que gobernaba la forma en la que podían cambiar las geometrías de las superficies curvadas se convirtió en el equivalente de las leyes de la física, que exigían la conservación de la energía y del momento en todos los procesos naturales. Y lo que es aún más notable: si se consideraba una situación en la que las masas fuesen pequeñas y sus movimientos lentos en comparación con la velocidad de la luz, la distorsión causada en la geometría del espacio sería minúscula, y las ecuaciones de Einstein se convertían simplemente en las que describían la vieja teoría de la gravitación de Newton.

Una digresión

Los errores son algo bueno. Cuantos más errores, mejor. La gente que se equivoca consigue promociones. Son personas de fiar. ¿Por qué? Porque no son peligrosos. Seguro que no son gente seria. La gente que no comete errores acaba cayéndose por un barranco, lo cual no es bueno, porque a alguien en plena caída libre se le considera un hándicap. Podría caerte encima.

James Church^[76]

El año 2000, se celebró una gran competición en Gran Bretaña. Se invitó al público a votar por el británico más importante de los últimos mil años. Los presentadores de programas de famosos luchaban con los periodistas de la prensa escrita para tratar de persuadir a los votantes para situar a William Shakespeare por delante de la princesa Diana y a David Beckham detrás de Charles Darwin. Un periódico de prestigio consideró el caso de Newton. Era un contendiente de peso —arco iris, movimiento, gravedad, cálculo y todo eso—, pero el periodista no estaba convencido. Einstein demostró que algunas de las teorías de Newton estaban indudablemente «equivocadas», escribió.

Este comentario traicionaba un sutil malentendido acerca del progreso de la ciencia moderna. Cuando apareció la teoría de la gravedad de Einstein y fue confirmada en un detalle cada vez mayor por los experimentos, eso no suponía que hubiese que desechar la teoría de Newton. Llegará un punto en que la teoría de Einstein quedará superada, pero tampoco la desecharemos.

Las ideas de Einstein extendían la teoría de Newton de modo que pudiésemos entender lo que sucedía cuando la gravedad era muy intensa y la velocidad de los movimientos se aproximaba a la de la luz. La teoría de Newton no podía hacer frente a estas situaciones extremas. Pero si se examina la forma de la teoría de Einstein en el caso límite de movimientos mucho más lentos que la velocidad de la luz y de gravedad débil, cada vez se parece más a la teoría de Newton; la teoría de Newton es una aproximación al límite de la teoría de Einstein. Sustituye la teoría de Newton en el ámbito de su aplicación y en la gama de situaciones en las que puede aplicarse, pero no la reemplaza como descripción válida del mundo cotidiano, en el que los movimientos son lentos y la gravedad es débil. Por eso los estudiantes de ingeniería estudian las leyes de Newton, y puedo predecir sin temor a equivocarme que seguirán haciéndolo de forma muy similar en el próximo milenio.

Una visión similar se puede aplicar a la forma en que la mecánica cuántica de Werner Heisenberg y Paul Dirac sustituyó a la mecánica newtoniana. La mecánica cuántica amplió el dominio de nuestra comprensión de la mecánica hasta el ámbito de distancias e intervalos de tiempo muy reducidos, y al movimiento de partículas de muy poca masa y fotones de luz. Y sin embargo, si dejamos que las cosas crezcan apropiadamente^[77], la mecánica cuántica se parece cada vez más a la de Newton.

En la evolución de nuestras teorías físicas, las nuevas teorías incluyen los éxitos y aciertos de sus predecesoras. Amplían su dominio de aplicación y la gama de situaciones que son capaces de describir con precisión. Las nuevas teorías no derrocan a las antiguas y las relegan a la papelera de la historia. Quizá eso fuese posible hace mucho tiempo, cuando la teoría en vigor apenas tenía pruebas que la sostuviesen y carecía de poder explicativo. Actualmente, una teoría nueva necesita poder explicar todo aquello que ya ha sido bien explicado y algo que aún no lo haya sido, y debe tener la capacidad de predecir algo en lo que nadie había pensado antes.

La creación del universo de materia en reposo de Einstein

Las personas se equivocan cuando dicen que la ópera ya no es lo que era. Sí es lo que era. Ese es el problema.

Noël Coward^[78]

Einstein anunció al mundo de la ciencia su nueva teoría de la gravitación en noviembre de 1915, en un artículo publicado en la augusta Actas de la Real Academia Prusiana de Ciencias. Había tardado más de diez años en resolver satisfactoriamente el problema de la gravedad y deducir un conjunto de ecuaciones que pudiese hallar en todos los casos cómo curvarían la masa y la energía el espacio y cómo se moverían según la organización de este. Su teoría predecía con exactitud los misteriosos 43 segundos de arco por siglo de bamboleo de la órbita del planeta Mercurio, un problema que llevaba desafiando a los astrónomos desde que el astrónomo francés Urbain Le Verrier lo descubriera en 1859. La teoría de Newton no podía dar una explicación satisfactoria^[79]. Para Einstein, fue la síntesis de la formulación matemática y la física —la forma en que las leyes de la física surgían, casi sin invitación, de las matemáticas abstractas— lo que despertó su entusiasmo, hasta el punto de escribir a un amigo suyo que «No creo que nadie que haya entendido esta teoría pueda sustraerse a su hechizo»^[80].

Dieciocho meses más tarde, el 8 de febrero de 1917, en mitad de la primera guerra mundial, Einstein anunció la primera aplicación de su nueva teoría al universo en su conjunto. Cada una de las soluciones de sus ecuaciones describía un posible universo. Y sin embargo, parecía que solo había un universo; entonces, ¿cómo se filtran las posibilidades no deseadas? Einstein luchó con ahínco y durante mucho tiempo con esta cuestión. Si permitía que el universo fuese infinito no veía la forma de que sus ecuaciones supusiesen restricción alguna a su comportamiento a una distancia infinita. Si es finito, debía evitar que el espacio tuviese un «borde».

A partir de los resultados que habían captado la atención de Schwarzschild, Einstein se dio cuenta de la importancia de un espacio con curvatura positiva. Era finito pero, como la superficie de una pelota, carecía de borde. Einstein creía también en la simetría: en promedio, el universo debía ser igual en todas direcciones y en todos los lugares. Así que, aunque la curvatura del espacio sufriría pequeñas variaciones por todas partes, igual que la superficie de un mar en calma, contemplado a gran escala sería aproximadamente igual en todas partes y en todas direcciones en cada momento. Una de las consecuencias interesantes de la curvatura del espacio es que, aunque las cosas tienen el mismo aspecto en todas direcciones, eso no significa que uno se encuentre en el centro del universo. Si recorres como una hormiga la superficie de una esfera, estés donde estés las cosas son iguales en todas direcciones, pero la superficie carece de centro^[81].

Pero Einstein flaqueó antes de dar un salto monumental. Utilizando todas estas hipótesis simplificadoras no pudo encontrar universos que estuviesen en reposo; todos los posibles mundos debían cambiar con el tiempo, en todas partes, expandiéndose o contrayéndose. Este resultado era totalmente inesperado. El espacio podía estar curvado, pero para Einstein en 1917 debía ser un escenario estático y fijo en el que las estrellas se movían. La única forma que se le ocurrió de hallar un universo inmutable fue introducir en sus ecuaciones una posibilidad que hasta entonces había dejado de lado.

La teoría de la gravitación de Newton señala que la fuerza de atracción gravitatoria entre dos masas las hacía acelerar una hacia la otra. Para detener esta aceleración es necesario un efecto de repulsión en sentido contrario para que la aceleración global percibida por las masas sea:

Aceleración = − (fuerza gravitatoria de atracción) + (fuerza de repulsión)

La teoría de Einstein permitía que esa fuerza de repulsión existiese, pero no lo exigía: se trataba de algo opcional. Parece ser un complemento que la Naturaleza no ha utilizado, porque no hay pruebas de ella al estudiar la gravedad en la Tierra ni sus efectos en el sistema solar. Sus efectos se debilitan cada vez más a pequeñas separaciones entre masas, pero se hace más fuerte cuando la separación aumenta^[82]. Esto significa que existe alguna distancia en el universo a la que la fuerza repulsiva será igual a la fuerza atractiva de la gravedad. Para un universo de ese tamaño específico no hay ni expansión ni contracción. Esto es el universo estático de Einstein.

Recordemos que el espacio de este universo tiene curvatura positiva, así que puede tener un volumen finito y, sin embargo, no tener límite. Si dibujamos una gráfica con el tiempo hacia arriba y el espacio (segmentos bidimensionales de espacio en cada momento) perpendicular a la flecha del tiempo, la ruta a través del espacio y el tiempo que recorre alguien en el universo de Einstein se enrosca en espiral alrededor de la superficie de un cilindro (Figura 3.3). Si observamos una nave espacial alejándose de nosotros, primero se hará más pequeña, pero luego regresa y se vuelve a hacer mayor. El tiempo que tarda la luz en dar toda la vuelta a este universo^[83] viene determinado por el promedio de densidad de materia que contiene^[84]. Para un universo con una densidad igual a la del aire que nos rodea, el viaje de ida y vuelta es de unos 2,5 días. En un universo de esas características podríamos ver lo que estábamos haciendo hace 2,5, 5, 7,5, 10, etc. días, cada vez que la luz completase circuitos del cosmos en su trayectoria hacia nosotros desde el pasado.

El universo de Einstein demuestra la fuerza del concepto heredado de un espacio estático que también había utilizado Schwarzschild. Introdujo un modelo de universo asombroso: un espacio finito curvado sin límite que existe durante toda la eternidad pasada y futura. Fue el primero que se deducía de sus extraordinarias ecuaciones, pero él había suprimido lo que las ecuaciones trataban de decirle: el universo no quería ser estático. Más adelante, Einstein calificaría su respuesta como «la peor metedura de pata de mi vida».

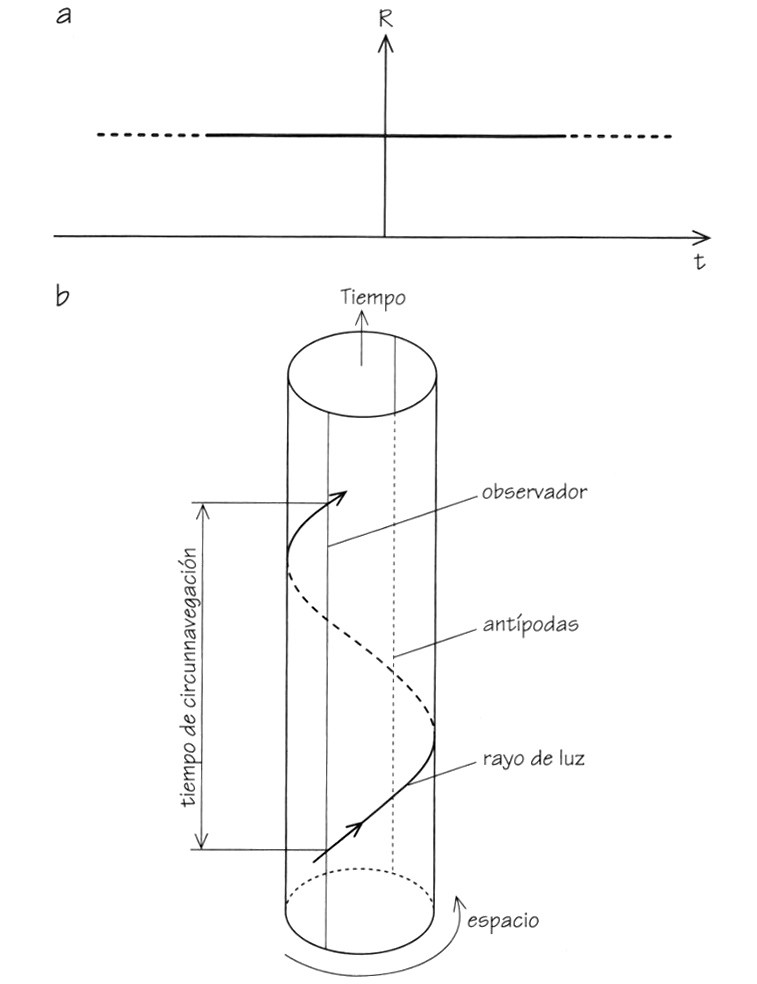
FIGURA 3.3. (a) Distancia, R, en función del tiempo, t, en el universo estático de Einstein. No hay cambio alguno en la separación de las partículas libres en el universo, (b) Diagrama que muestra la trayectoria a través del espacio y el tiempo de un rayo de luz que se mueve por el espacio del universo estático de Einstein a medida que pasa el tiempo. El rayo traza una hélice en la superficie de un cilindro.

El segundo universo: el universo de movimiento sin materia de De Sitter

Estoy muy interesado en el universo. De hecho, me estoy especializando en el universo y en todo lo que lo rodea.

Peter Cook

El siguiente científico que investigó las ecuaciones de universos de Einstein fue un distinguido astrónomo holandés llamado Willem De Sitter (1872-1934), que aprovechó la neutralidad de Holanda en la guerra para conocer a Einstein y mantener correspondencia con él^[85]. También mantuvo un estrecho contacto con astrónomos británicos, en particular con Arthur Eddington, que era el responsable de planificar el programa de oradores en las reuniones mensuales de la Royal Astronomical Society en Piccadilly durante el año 1917. En la tercera de su serie de presentaciones en la Society, De Sitter dio a conocer una nueva solución a las ecuaciones de Einstein^[86].

De Sitter conservó la nueva fuerza repulsiva de Einstein, pero decidió adoptar la hipótesis de que la densidad de materia en el universo era cero. Está claro que el universo real no está vacío, pero De Sitter supuso que la densidad era tan baja que los efectos de la atracción gravitatoria ejercida por la masa eran totalmente despreciables en comparación con los de la fuerza repulsiva de Einstein, a la que ya se denominaba fuerza «lambda» por la letra griega lambda (Λ) utilizada para denotarla. A diferencia del universo de Einstein, la geometría del universo de De Sitter era euclidiana, y su extensión era infinita.

Aunque el universo de De Sitter era fácil de hallar, no era tan fácil interpretarlo. Este universo parecía sugerir que la longitud de onda de la luz procedente de objetos distantes se «estiraría», de modo que su color parecería más rojo, y el estiramiento aumentaría a medida que se incrementaba la distancia de la fuente de luz con respecto a nosotros. Este efecto se denominó «efecto De Sitter». En 1912, el astrónomo norteamericano Vesto Slipher había descubierto un desplazamiento significativo en una longitud de onda identificable de la luz procedente de una distante nebulosa (o «galaxia», como la llamaríamos ahora); cinco años más tarde, informó de sus observaciones de corrimientos hacia el rojo en más de veinte nebulosas más, pero no sabía explicar ni interpretar estos desplazamientos. De Sitter mostraba ahora que su solución de las ecuaciones de Einstein provocaba precisamente este efecto. Un escrutinio más detenido reveló la razón: el universo de De Sitter se expandía. Si se introducían dos puntos de referencia en él, se alejarían acelerándose, y su separación aumentaría exponencialmente con el tiempo. El cambio de la separación entre dos puntos de referencia en función del tiempo en el universo de De Sitter se muestra en la Figura 3.4: su separación acelera a medida que pasa el tiempo.

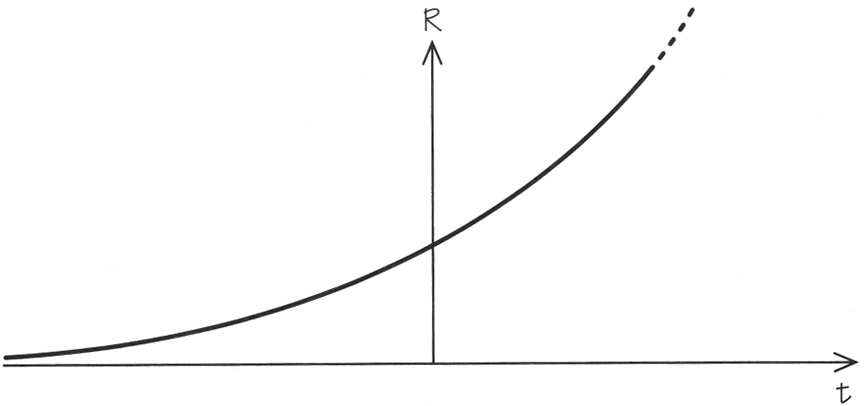
FIGURA 3.4. El universo acelerado de De Sitter. Las separaciones entre partículas libres crecen exponencialmente con el paso del tiempo.

En esta imagen de un universo en expansión, la interpretación del «efecto De Sitter» era simple. Cuando una estrella que se aleja emite ondas de luz, su longitud de onda se «estira», y las recibimos con una frecuencia menor a aquella con la que se emitieron. Esto se aplica a todas las ondas; en particular, a las de sonido y a las luminosas. Cuando el origen de la onda se acerca a nosotros sucede lo contrario. Una fuente de luz que se aleja parece más roja, pero una que se acerca parece más azul. El tono de una onda de sonido que se aleja es más grave; el de una onda que se acerca, más agudo. Este fenómeno se denomina «efecto Doppler», por el físico austríaco Christian Doppler, que lo descubrió en 1842 al buscar una explicación para la diferencia de colores de las estrellas móviles^[87]. El caso del sonido nos resulta conocido. Recordemos el característico ruido de una motocicleta pasando a toda velocidad junto a nuestro dormitorio a las 3 de la madrugada: iiiiii-uuuuuu. Al principio se dirige hacia nosotros, el tono del motor sube (iiiii), luego pasa de largo y las ondas de sonido proceden de una fuente que se aleja, por lo que su frecuencia se reduce y el tono cae (uuuu).

Las observaciones de Slipher eran coherentes con las ondas de luz que nos llegan procedentes de estrellas que se mueven radialmente alejándose de nosotros en un lado de nuestra galaxia y acercándose desde el otro lado. Por supuesto, era posible que Slipher hubiese visto simplemente objetos a la deriva, que se acercaban a nosotros desde una dirección y que se alejaban una vez nos habían superado. Poco a poco, las observaciones de ambos lados de la galaxia mostraban objetos que se alejaban, pero Slipher se aferró a su hipótesis del desplazamiento para explicar el corrimiento al rojo. Para él (y para nadie en aquella época) no había motivo para pensar que todo el universo se estuviese expandiendo, ni siquiera para pensar qué podía significar eso.

El universo matemático de De Sitter describía un universo en el que el propio espacio se expandía, acelerado por la nueva fuerza lambda de Einstein. Por desgracia, nadie quiso conectar esto con las observaciones de Slipher en 1917, ni siquiera De Sitter. Llegado 1921, De Sitter sabía que veintidós de las galaxias espirales que Slipher observaba se alejaban de nosotros. Nadie sabía a qué distancia se hallaban, y seguía siendo posible que los responsables fuesen movimientos locales aleatorios y no una expansión global y sistemática del universo. De Sitter se resistía a extraer conclusiones firmes de las observaciones de Slipher. Aunque había hallado el primer universo en expansión, estaba muy disimulado. Pasaría un tiempo antes de que revelase su verdadera personalidad.

El universo de De Sitter resultará ser de una importancia capital para nuestra actual comprensión del universo. Posee algunas características notables. Se hace cada vez mayor, y no tiene principio ni fin. Aunque es cada vez más pequeño si se retrocede en el tiempo, nunca llega a un tamaño cero, y no hay un principio aparente en el que el tamaño sea cero y la densidad de materia infinita. El ritmo de expansión tiene un valor constante y es siempre el mismo. Si uno aparece de pronto en un momento cualquiera de la historia de este universo, no hay forma de ubicarse en el tiempo: el futuro es imposible de distinguir del pasado. Todo lo que se puede observar es siempre igual. La historia no es un asunto importante en el mundo de De Sitter.

Los universos de materia en movimiento de Friedmann

Tenemos el espacio de Einstein, el espacio de De Sitter, universos que se expanden, universos que se contraen y universos que vibran. De hecho, el matemático puro puede crear universos con solo escribir una ecuación; si es un individualista, puede incluso tener un universo para él solo.

J. J. Thomson

Einstein era físico, De Sitter era astrónomo, pero el siguiente participante famoso en el juego de buscar universos era un joven y desconocido matemático y meteorólogo de San Petersburgo llamado Alexander Friedmann^[88]. Cuando era un joven estudiante de física tuvo la suerte de asistir a las clases de teoría cuántica y relatividad impartidas por el notable físico austríaco Paul Ehrenfest, que fue profesor en la Universidad de San Petersburgo entre 1907 y 1912 antes de trasladarse a Leiden. Friedmann se mantuvo en contacto con Ehrenfest después de graduarse y empezar a trabajar como meteorólogo en el observatorio de Pavlovsk, y posteriormente como estudiante investigador del noruego Vilhelm Bjerknes (fundador de la meteorología teórica moderna) en Leipzig. Tras sus servicios en el campo de la balística en el frente de Austria durante la primera guerra mundial^[89], volvió a su labor académica y progresó con rapidez. Trabajó en matemáticas, mineralogía y ciencias de la atmósfera, y finalmente se convirtió en profesor de matemáticas y física en la Universidad Estatal de Perm, una nueva institución dependiente de la Universidad de San Petersburgo, en 1918. Allí sufrió las consecuencias de la guerra civil; la ciudad de Perm fue ocupada primero por los «rusos blancos» y luego por el Ejército Rojo de Trotski, lo que supuso la partida de muchos de sus colegas. En 1920, Friedmann se trasladó al Observatorio Geofísico de San Petersburgo, donde empezó a conocer la nueva teoría de la relatividad general de Einstein. La notable amplitud de los conocimientos de Friedmann iba desde el trabajo puramente teórico en matemáticas hasta espectaculares vuelos en globo a gran altura para investigar los efectos de la altura sobre el cuerpo humano. En 1925, durante un tiempo, poseyó junto con un colega el récord mundial de altitud en globo, ya que ascendió hasta 7400 metros. Murió pocos meses más tarde, al parecer de fiebre tifoidea, a la edad de treinta y siete años^[90].

Friedmann había aprendido en gran detalle las formidables matemáticas que se hallaban tras las ecuaciones de Einstein, y decidió ponerse a buscar soluciones generales de estas, más allá de las halladas por Einstein y De Sitter, pero manteniendo las hipótesis de estos: que el universo es igual en todas partes y en todas direcciones. Sus dos escritos, publicados en 1922 y 1924, y su libro El mundo en espacio y tiempo, escrito en 1923, revelan que Friedmann conocía los universos hallados por De Sitter y Einstein, pero al parecer ignoraba el descubrimiento de Slipher del corrimiento hacia el rojo de la luz de las estrellas distantes. Su enfoque de las ecuaciones de Einstein era el de un matemático en busca de soluciones. Y las encontró.

FIGURA 3.5. Alexander Friedmann (1888-1925).

Primero descubrió la posibilidad de un universo finito «cerrado», con un espacio con curvatura positiva que se expande desde un principio situado un tiempo finito en el pasado hasta un tamaño máximo y luego se contrae de nuevo hasta un fin situado un tiempo finito en el futuro (véase la Figura 3.6). Se trataba del caso de un universo en expansión que contenía materia ordinaria que no ejercía presión. Era finito en masa y volumen y finito en tiempo total de vida; Friedmann hizo incluso una estimación de que su masa sería de alrededor de 5 × 10²¹ veces la masa de nuestro Sol, si la duración total de un ciclo completo era de unos 10 000 millones de años^[91]. Empezó con lo que más tarde se llamaría un big bang de densidad infinita y se contrajo hasta su fin en un similar y extremo big crunch. En su libro, Friedmann reflexionaba sobre el hecho de que podía imaginar esta solución hacia delante (y hacia atrás) en el tiempo, de modo que el universo podía oscilar en una serie interminable de ciclos de expansión y contracción (como se muestra en la Figura 3.7), y señalaba que:

puede haber casos en los que el radio de curvatura del mundo […] cambie permanentemente. El universo se contrae hasta un punto (hasta la nada) y luego aumenta de nuevo su radio desde un punto hasta un cierto valor, y otra vez disminuye su radio de curvatura para transformarse en un punto, etc. Es difícil no pensar en las historias de la mitología india y sus períodos de vida. También se puede hablar de la creación del mundo a partir de la nada. Pero, por el momento, todo esto debe considerarse como una curiosidad que no puede comprobarse debido a observaciones astronómicas inadecuadas^[92].

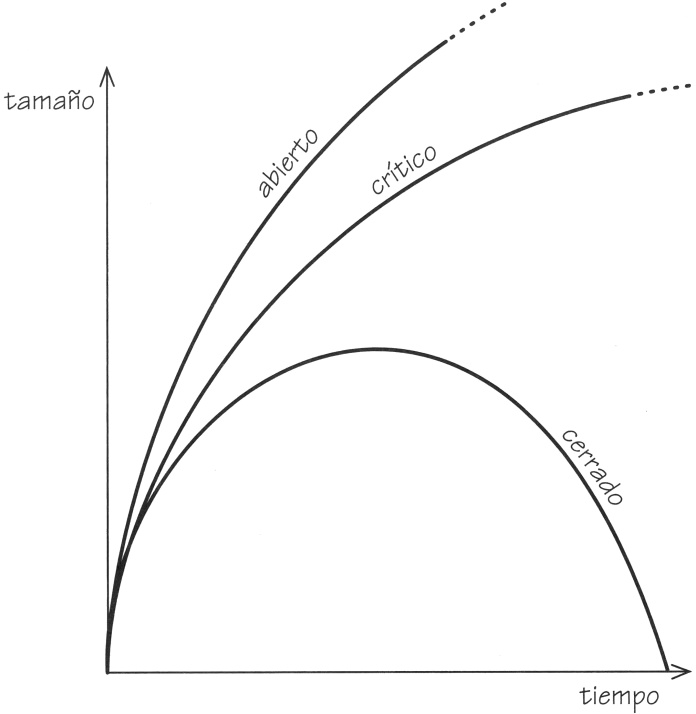
FIGURA 3.6. Los universos en expansión y en contracción de Friedmann.

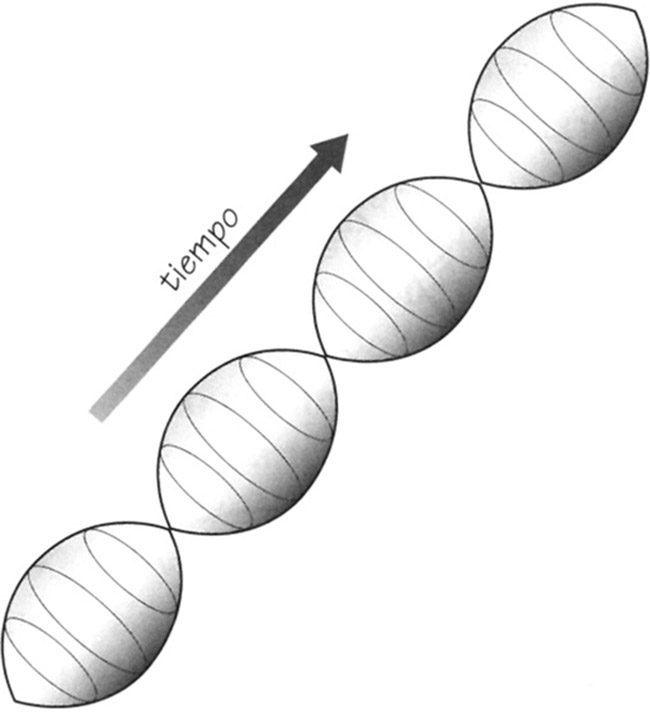
FIGURA 3.7. El universo oscilante de Friedmann.

Friedmann se dio cuenta entonces de que también había soluciones de las ecuaciones de Einstein en las que la curvatura del espacio era «abierta» y negativa, como una silla de montar, de modo que el volumen del universo es infinito, se empieza a expandir desde un principio situado en un pasado finito y se sigue expandiendo siempre^[93]. Estas soluciones se muestran también en las Figuras 3.6 y 3.7.

Así, Friedmann fue el primero en descubrir que las ecuaciones de Einstein permitían la existencia de universos en expansión y en contracción que contuviesen materia ordinaria, como planetas y estrellas. Las observaciones astronómicas no lo estimularon, ni hizo demasiado hincapié en el significado físico del principio o el fin de estos universos en el tiempo. Es también de interés su descripción de un universo que aparece de la nada (y desparece de nuevo en ella). Por desgracia para Friedmann, nadie parece haberse percatado de sus trascendentales descubrimientos. Publicó sus estudios en Zeitschrift für Physik, una importante revista de investigación en su momento, en la que Einstein publicó algunos de sus trabajos; y sin embargo, no hubo comentario alguno acerca de sus nuevos «universos». Y lo que es peor, Einstein pensaba que Friedmann se había equivocado en los cálculos y que estos universos en expansión y contracción no eran realmente soluciones de sus ecuaciones, y publicó una nota en la revista manifestándolo.

Por suerte, uno de los colegas de Friedmann en San Petersburgo, Yuri Krutkov, viajó a Leiden en mayo de 1923, donde se reunió con Einstein y pudo convencerlo de que los cálculos de Friedmann eran correctos: realmente había universos no estáticos como soluciones a sus ecuaciones. Einstein actuó con rapidez y publicó otra breve nota en la revista en la que decía que, tras haber mantenido correspondencia con Friedmann y haber debatido con Krutkov, reconocía que había cometido un error de cálculo y que las soluciones de Friedmann eran «correctas y explicativas. Muestran que, aparte de las soluciones estáticas a las ecuaciones de campo, hay soluciones que varían con el tiempo»^[94]. Curiosamente, en la versión manuscrita de esta nota a la revista, Einstein añadía una última frase en la que decía que, a pesar de su corrección, «difícilmente se puede atribuir a estas soluciones un significado físico». Por fortuna, borró esa frase antes de que la carta se publicase.

A Friedmann no le quedaba mucho tiempo de vida, y no desarrolló sus descubrimientos dándoles una interpretación astronómica. Para él no eran más que ejercicios matemáticos. Uno de sus colegas, Vladimir Fock, afirmó que Friedmann le comentó una vez que «su tarea era indicar las posibles soluciones de las ecuaciones de Einstein, y que los físicos podían hacer lo que quisiesen con esas soluciones^[95]» Pero actualmente, el nombre de Friedmann es el más vinculado a la palabra «universo». Si se efectúa una búsqueda en Google de «Friedmann’s universe» (sin las comillas), se obtienen más de un millón de resultados.

Los universos de Lemaître

La evolución del mundo se puede comparar a un espectáculo de fuegos artificiales que acaba de terminar: algunas volutas rojas, cenizas y humo. Subidos en nuestros fríos rescoldos, vemos cómo los soles se apagan lentamente y tratamos de recordar su brillo ya desvanecido.

Georges Lemaître^[96]

Georges Lemaître fue ordenado sacerdote católico en el seminario Maison Saint-Rombaut en 1922, después de recibir la Cruz Militar en la primera guerra mundial. La guerra había interrumpido sus estudios, y se graduó en matemáticas después de ser contratado para dar clases de ingeniería en la Universidad Jesuita de Lovaina, Bélgica, en 1920. Ganó una beca para estudiar en el extranjero y pasó el curso 1923-1924 en St. Edmund’s House^[97] en Cambridge, trabajando con Arthur Eddington como alumno visitante en los observatorios de la Universidad. Podría decirse que Eddington era el astrofísico de mayor talento del mundo en aquella época, y se había apuntado una notable lista de logros: comprender el funcionamiento de las estrellas, desarrollar teorías sobre movimiento estelar en nuestra galaxia, y la dirección de una famosa expedición que en 1919 se dirigió a la isla portuguesa de Príncipe, junto a la costa occidental de África, a fin de comprobar la predicción de Einstein de que los rayos de luz de las estrellas distantes se desviarían de la línea recta debido al efecto de la gravedad del Sol. También había escrito el primer texto avanzado en inglés en el que se explicaba la teoría general de la relatividad de Einstein.

La capacidad matemática de Eddington era legendaria, y había desarrollado una profunda comprensión de la teoría gravitatoria de Einstein con gran rapidez. También desempeñó un papel esencial en la conservación de los vínculos con los científicos de la Europa continental durante la primera guerra mundial a través de su posición de secretario de la Royal Astronomical Society y, como cuáquero convencido, de su no participación en la guerra. Sorprendentemente, Eddington se salvó de la vergüenza social y probable encarcelamiento que hubiese resultado de su objeción de conciencia al servicio militar en 1917 por la intervención del Astrónomo Real, Sir Frank Dyson. Haciendo uso de su estrecha conexión con el Almirantazgo, Dyson negoció un acuerdo mediante el cual el servicio militar de Eddington sería aplazado; si pasado el plazo la guerra había acabado, dirigiría una de las dos expediciones planificadas por el Almirantazgo para observar el eclipse total de sol del 29 de mayo de 1919 y así comprobar la teoría general de la relatividad de Einstein.

Lemaître no estudió cosmología con Eddington durante el año que pasó como alumno visitante en Cambridge, pero aprovechó la oportunidad para desarrollar una profunda comprensión de la relatividad general. Después de su período en Cambridge se puso a trabajar en su doctorado con el famoso astrónomo norteamericano Harlow Shapley en el Observatorio de Harvard, y se graduó en el vecino Massachusetts Institute of Technology en julio de 1927 (el Observatorio no empezó a conceder doctorados hasta 1929). Eddington había quedado enormemente impresionado por la brillantez y la capacidad matemática de Lemaître, y lo recomendó de forma decidida en carta a otros científicos. Lemaître era además una persona extremadamente gregaria y amistosa, que se llevaba bien con todo aquel con el que coincidía en sus viajes científicos. Sin duda, este factor alentó la colaboración y el intercambio de ideas.

Durante su estancia en Boston, Lemaître adquirió una aguda comprensión del problema de los corrimientos hacia el rojo, y ya había leído los primeros trabajos de Einstein sobre el modelo del universo estático. Ni él ni Eddington conocían el trabajo de Friedmann. Llegado el año 1927, Lemaître había preparado el más completo de los estudios sobre los universos más simples que predecía la teoría de Einstein. El estudio iba más allá de Einstein, De Sitter y Friedmann, introduciendo la posibilidad de que el universo contuviese, aparte de estrellas y galaxias, radiación con una presión significativa. También intentó explicar los corrimientos hacia el rojo —observados por primera vez por Slipher— mediante el desplazamiento Doppler en un universo en expansión.

El impresionante trabajo de Lemaître de 1927, publicado primero en francés en una recóndita revista belga, es el primero que combina las soluciones de universo en expansión de las ecuaciones de Einstein con su interpretación física y con un cálculo del desplazamiento hacia el rojo de la luz de las estrellas distantes en forma de efecto Doppler^[98]. Como sucede en todo su trabajo, Lemaître exhibe una magnífica claridad, sin utilizar matemáticas innecesarias pero captando todos los aspectos esenciales desde el punto de vista físico^[99]. Lemaître estimaba que el universo carecía de centro y de bordes, que podía ser finito o infinito y que las ecuaciones de Einstein tienen una interpretación simple en términos de conservación de la energía y termodinámica. Incluso llegó a calcular el ritmo actual de expansión del universo a partir de los datos observacionales disponibles sobre corrimientos hacia el rojo y distancias de cuarenta y dos galaxias, y ofreció la primera determinación de la denominada «constante de Hubble», H, obteniendo un valor de 625 km por segundo por megapársec, similar al hallado por Hubble dos años más tarde. Calculó la relación entre sus velocidades de recesión (ν) y sus distancias (r)^[100] y obtuvo la primera deducción de la «ley de Hubble» (ν = Hr) empleando el efecto Doppler.

Hubble publicaría sus propias pruebas de esta ley en 1929, y a continuación De Sitter hizo un análisis de los mismos datos (lo que enojó bastante a Hubble, que los consideraba de su propiedad, aunque estaban publicados y De Sitter citó su fuente) en 1930. Hubble nunca estuvo realmente de acuerdo con las implicaciones físicas globales de un universo en expansión, ni utilizó sus observaciones específicamente para apoyar modelos teóricos. Calificaba las velocidades de las galaxias distantes como «aparentes» y dejaba la interpretación a otros^[101]. Sin embargo, De Sitter y Lemaître adoptaron la imagen del universo en expansión con entusiasmo.

El trabajo de Lemaître sirvió también para aclarar el estatus del universo estático de Einstein y del mundo vacío con expansión exponencial de De Sitter. Lo que Lemaître había mostrado era que el mundo de Einstein era inestable. Si el universo empezaba con un estado estático, cualquier perturbación o movimiento dentro de él lo precipitaría a un estado gradual de expansión o de contracción (Figura 3.8). Era el equivalente cosmológico de una aguja en equilibrio sobre su punta.

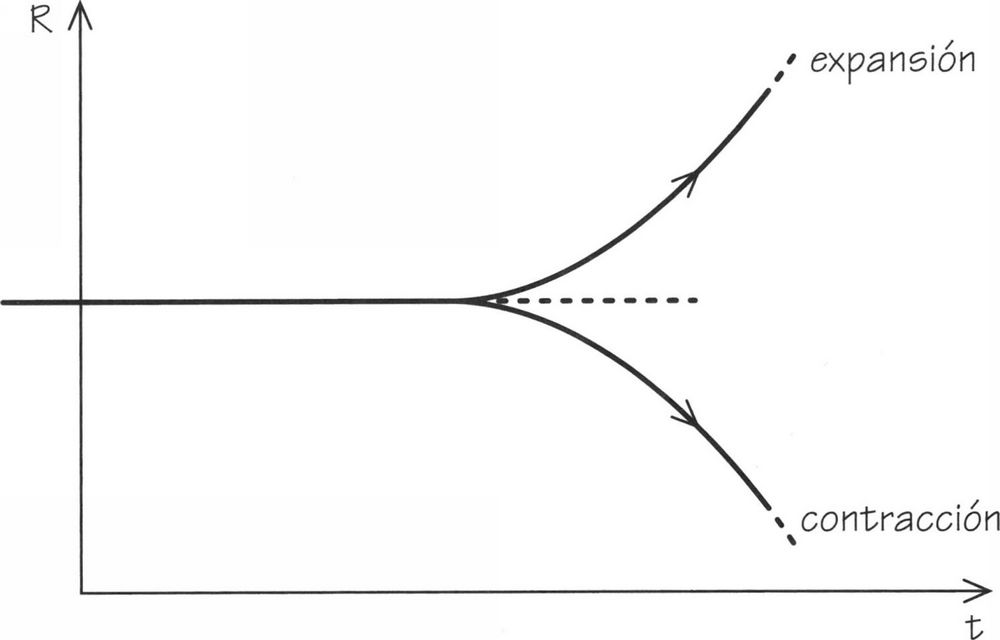
FIGURA 3.8. La inestabilidad del universo estático. Lemaître y Eddington demostraron que el mínimo movimiento de materia en un universo estático genera un estado de futura expansión o contracción.

FIGURA 3.9. Georges Lemaître y Albert Einstein en 1933.

Este descubrimiento, que al parecer no gustó demasiado a Einstein, fue el catalizador para que los universos de Lemaître se hiciesen conocidos. En 1930, su antiguo mentor, Arthur Eddington, ya había sospechado que el universo estático de Einstein era inestable ante pequeños cambios, y lo demostró introduciendo pequeñas irregularidades de densidad en la solución de Einstein y demostrando que todas ellas crecían. Aunque era ajeno al trabajo de Lemaître, poco después de publicar^[102] su descubrimiento tuvo la sorpresa de recibir una carta de su antiguo alumno señalando que la inestabilidad del universo de Einstein ya había sido demostrada (de una forma distinta) en su trabajo de 1927. Eddington había olvidado esa parte del trabajo y no recordó su importancia para los cálculos que había llevado a cabo. Eddington actuó con rapidez, escribiendo una carta a la revista Nature en junio de 1930, en la que señalaba que el trabajo de Lemaître no había sido reconocido, y disponiendo la aparición de la traducción al inglés del artículo de 1927 en el revista Monthly Notices of the Royal Astronomical Society en 1931^[103]. El resultado fue que Lemaître se convirtió en el cosmólogo teórico más famoso de la época. Lemaître no supo nada del anterior trabajo matemático de Friedmann hasta una conferencia celebrada en octubre de ese mismo año, pero añadió una cita en la traducción de 1931 de su artículo.

FIGURA 3.10. Lemaître dando una clase de mecánica celeste.

En 1957, dos años después de la muerte de Einstein, Lemaître concedió una entrevista para hablar de sus encuentros con Einstein; en ella reveló que, en la conferencia Solvay celebrada en 1927, durante una conversación privada, Einstein había elogiado la elegancia matemática de su artículo, hablándole del trabajo anterior de Friedmann, pero que desde un punto de vista físico consideraba que las cosmologías no estáticas eran «abominables»^[104]. Lemaître aún creía que Einstein no había asumido realmente la trascendencia de las nuevas observaciones astronómicas de galaxias alejándose para las soluciones de universo en expansión de su teoría. Sin embargo, en 1933, después de asistir a una conferencia de Lemaître sobre el asunto en Pasadena, Einstein quedó convencido de la simplicidad del punto de vista de Lemaître y describió su imagen de un universo en expansión a partir de un principio de calor extremo como la explicación «más bella» del comportamiento del universo.

El universo de Lemaître era similar al que Eddington descubrió en su estudio de la inestabilidad del universo estático de Einstein. Se suele denominar universo de Eddington-Lemaître (Figura 3.11) y empieza en el infinito pasado en un estado estático que gradualmente se expande, de modo que la expansión pasa a ser perceptible un tiempo finito en nuestro pasado^[105]. A continuación se sigue expandiendo y se va convirtiendo en el universo de expansión exponencial de De Sitter al cabo de mucho tiempo. Posee la fuerza repulsiva de Einstein, lambda; su espacio tiene curvatura positiva y es de extensión finita, y se expande siempre.

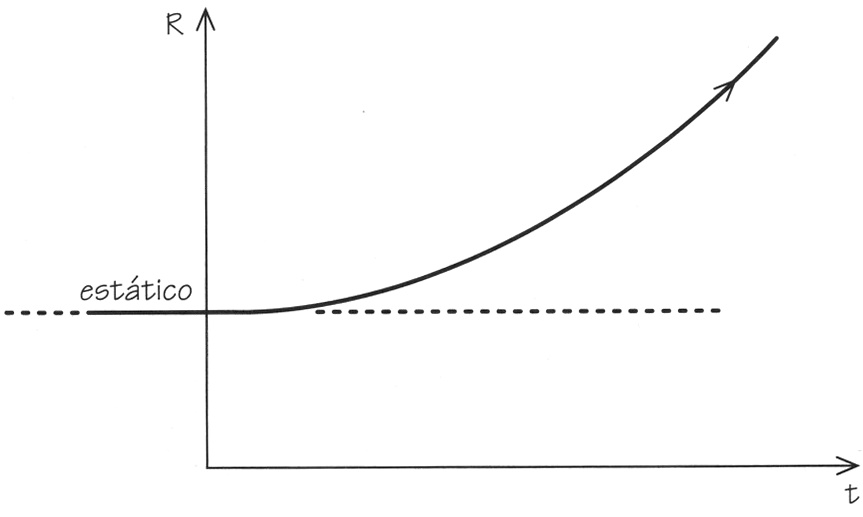
FIGURA 3.11. El universo de Eddington-Lemaître.

FIGURA 3.12. Arthur Eddington y Einstein en 1930, hablando en los terrenos del Observatorio de la Universidad de Cambridge, donde Eddington vivía con su hermana.

El pasado infinito implica que el universo no tiene principio, algo que no parecía preocupar ni a Eddington ni a Lemaître. De hecho, Eddington lo consideraba una propiedad natural, que daba al universo «un tiempo infinito para empezar», porque «no hay prisa para que nada empiece a suceder»^[106]. Opinaba que un universo con un inicio brusco en el tiempo, como el de Friedmann, era «repugnante», una simple «teoría pirotécnica», en contraste con su propia concepción «plácida», que era más probable que se ajustara a nuestro sentimiento general de tranquilidad. Eddington también sostenía que, aunque había una historia infinita pasada, solo habría un pasado finito durante el cual pudiesen suceder cosas, porque el universo estaba demasiado cerca del equilibrio térmico total para que hubiese una acumulación de entropía suficiente desde su pasado infinito (Figura 3.13). Por tanto, creía que este tipo de universo no llegaría a la muerte térmica ocasionada por una acumulación de una cantidad inaceptable de entropía y desorden a lo largo de su pasado infinito. Era geométricamente viejo pero joven desde la perspectiva termodinámica.

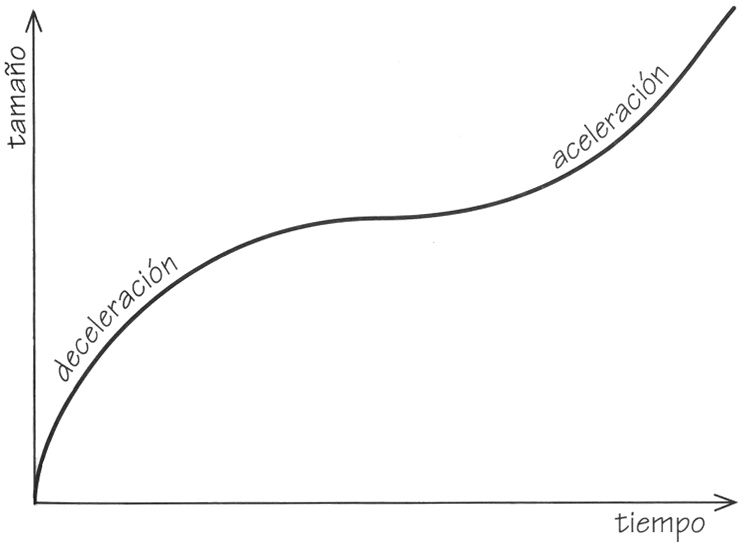
FIGURA 3.13. El universo de Lemaître empieza a expandirse desde un principio de big bang, como uno de los universos de Friedmann, se aproxima al universo estático antes de empezar a acelerar, y progresivamente se va pareciendo más al universo de De Sitter.

Uno podía haber esperado que las convicciones religiosas de Lemaître lo predispondrían hacia modelos del universo que tuviesen un principio en el tiempo. Pero no era el caso. Lemaître mantenía separados sus puntos de vista científico y religioso, y no veía que tuviesen puntos de posible conexión o conflicto; eran interpretaciones del mundo paralelas, pero diferentes. Para él, en la Biblia no se enseñaba ciencia, y buscar instrucción religiosa en la ciencia era como buscar dogmas católicos en el teorema del binomio^[107]. En una etapa posterior de su vida, cuando presidía la Academia Pontificia de las Ciencias, Lemaître escribió, acerca de su teoría del universo en expansión, que:

En lo que a mí respecta, esta teoría es totalmente ajena a cualquier cuestión metafísica o religiosa. Deja al materialista libertad para negar cualquier ser trascendente […] Para el creyente, elimina cualquier intento de familiaridad con Dios […] Está en consonancia con Isaías cuando habla del Dios oculto, oculto incluso en el inicio del universo.

Sin embargo, parecía ser partidario de uno de los muchos universos que halló en su artículo de 1927. Tenía un pasado finito y se expandía desde un inicio de calor extremo, decelerando primero y luego cambiando gradualmente a una expansión acelerada a medida que la constante cosmológica repulsiva pasaba a dominar sobre la fuerza de atracción gravitatoria de Newton, antes de seguir hacia una expansión de rapidez exponencial, como el universo de De Sitter (Figura 3.13). La curvatura de su espacio era positiva, como también lo era la constante cosmológica, igual que en el universo estático de Einstein, pero la repulsión positiva es ligeramente mayor que el muy especial valor elegido por Einstein, de modo que este universo se expande siempre.

El universo de Lemaître ha resultado ser la descripción más precisa de nuestro universo, con una edad total de 13 700 millones de años y una transición a la aceleración que tuvo lugar hace 4500 millones de años.

Mediante el claro análisis ofrecido por Lemaître, los cosmólogos pudieron analizar la galería completa de universos simples que se expanden al mismo ritmo en todos los puntos y en todas direcciones. Solo había dos magnitudes que podían cambiar: la curvatura del espacio podía ser positiva, negativa o cero (euclídea), y la fuerza constante cosmológica introducida por Einstein podía ser repulsiva (positiva), atractiva (negativa) o cero. La Figura 3.14 muestra una galería de todos los universos que se pueden obtener. El primero en tabularlos de esta forma fue Edward Harrison en 1967^[108].

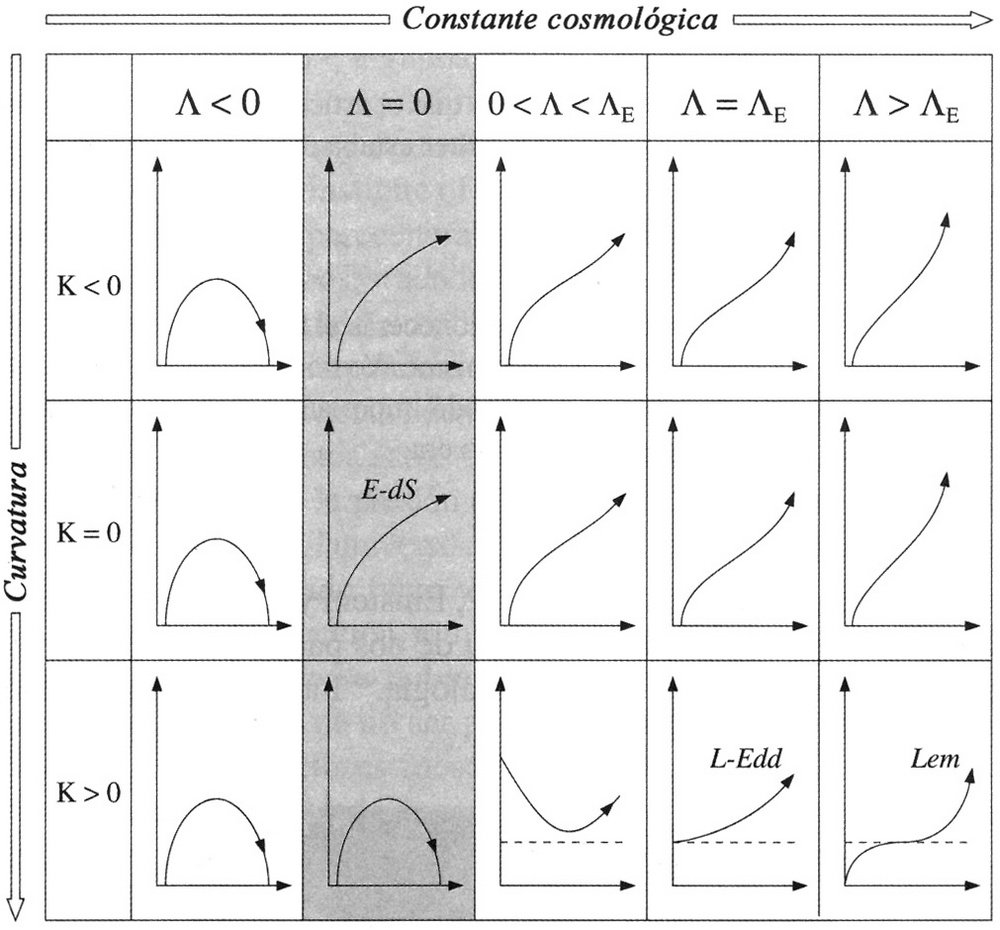
FIGURA 3.14. La galería de posibles universos de Friedmann-Lemaître, con los posibles cambios de distancia en función del tiempo para todas las combinaciones posibles de valores para la curvatura del espacio (K positiva, cero o negativa) y la constante cosmológica. El valor especial de la constante cosmológica, denotado por Λ_E, es el valor que da el caso especial del universo estático de Einstein (que se muestra con una línea de puntos) cuando la curvatura es positiva. Este universo estático es inestable, y eventualmente empieza a expandirse o a contraerse, como se muestra en los cuadros L-Edd y Lem.

El universo de Einstein y De Sitter

Yo no creo que el artículo sea muy importante, pero De Sitter estaba entusiasmado con él.

Albert Einstein

Supongo que conocerás el artículo escrito por Einstein y por mí mismo. Yo no considero que el resultado sea demasiado importante, pero Einstein parecía pensar que sí lo era.

Willem De Sitter^[109]

A principios de la primavera de 1932, Einstein y De Sitter unieron sus fuerzas para publicar una breve nota de dos páginas con la intención de simplificar el estudio de la cosmología^[110]. La galería de posibilidades reveladas por el trabajo de Lemaître conducían a muchos posibles universos en expansión; algunos se expandían eternamente, mientras que otros, como aquellos que Friedmann había hallado primero, acababan por dar la vuelta y contraerse. Einstein y De Sitter estaban de visita en el California Institute of Technology en Pasadena en esa época (en la Figura 3.15 aparecen trabajando juntos allí), y señalaron que, entre la profusión de posibilidades espacialmente uniformes e isótropas existía un universo de simplicidad máxima.

Si se asume que la curvatura del espacio es cero (de modo que la geometría del espacio sea euclídea), la constante cosmológica se establece en cero —Einstein tenía ganas de ver el retorno de su antigua idea— y se asume también que la presión de materia es cero, el resultado es un universo muy simple. El universo de Einstein-De Sitter se expande desde un principio en el pasado finito y lo hace eternamente (Figura 3.16^[111]).

FIGURA 3.15 Einstein y De Sitter trabajando juntos en su modelo de universo en Cal Tech, Pasadena, en 1932.

Esta era una deducción muy simple a partir de los trabajos ya realizados, y quizá no se hubiese considerado lo bastante original como para publicarlo de no ser por la celebridad de sus dos autores. De hecho, este modelo es inestable, como el universo estático de Einstein, en el sentido de que, si la curvatura no es exactamente cero, la expansión se separará gradualmente de la de Einstein-De Sitter hacia una expansión más rápida y divergente, o se ralentizará y se invertirá para convertirse en una contracción, como se muestra en la Figura 3.6. El universo de Einstein-De Sitter es la trayectoria intermedia que se muestra; los otros universos, el cerrado y el abierto, con una fuerza lambda igual a cero se separan a medida que el tiempo aumenta. La novedad de la sugerencia de Einstein y De Sitter, que ninguno de los dos consideró importante, es que, durante los siguientes sesenta años, ese modelo simple fue la mejor descripción de la expansión global de nuestro universo. El hecho de que el universo estuviese aún tan próximo a este ritmo especial de expansión indicaba que la inestabilidad no había tenido tiempo de desarrollarse de forma significativa. Pero el universo llevaba en expansión más de 13 000 millones de años, lo que sugiere que debía de haber empezado a expandirse a una distancia extraordinariamente breve del estado especial de Einstein-De Sitter. Este extraño estado de cosas se denominó más tarde el «problema de la planitud», y fue una de las motivaciones de la famosa teoría del universo inflacionario propuesta por Alan Guth en 1981, que volveremos a ver en capítulos posteriores.

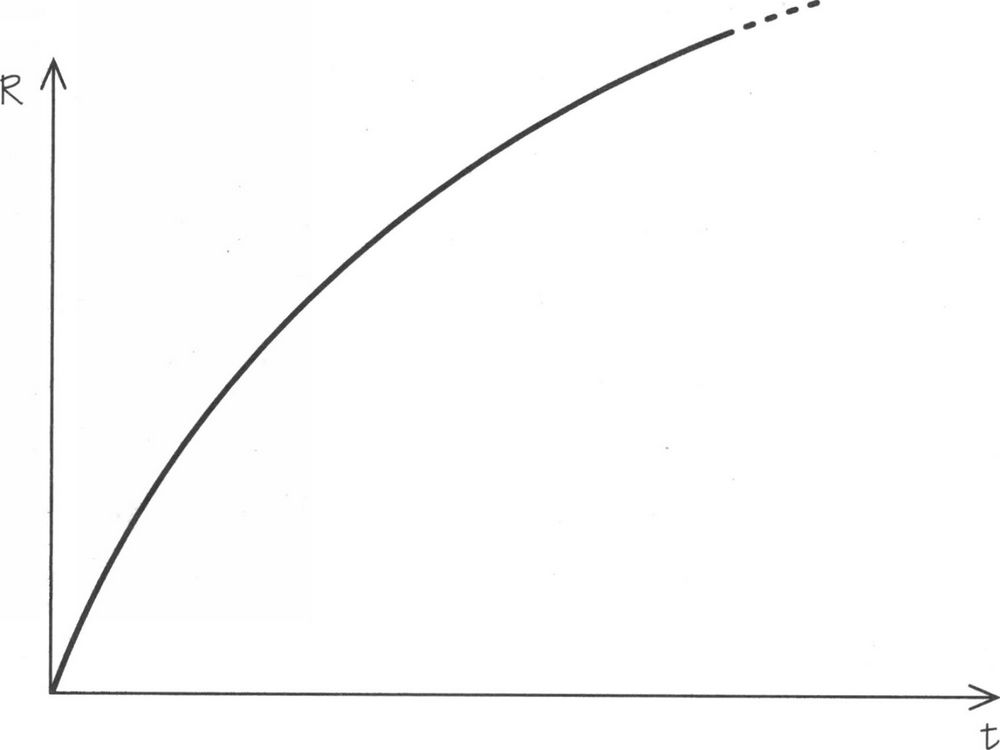
FIGURA 3.16. El universo de Einstein-De Sitter. Las distancias aumentan en proporción a la potencia dos tercios del tiempo.

Todos estos universos tienen una interpretación sencilla y esclarecedora que Newton hubiese comprendido de inmediato. Si se tira una piedra al aire, regresará a la Tierra: carece de la energía cinética suficiente para escapar del tirón gravitatorio de la Tierra. Pero si se puede lanzar a una velocidad superior a 11 km/s, ya no regresará^[112]. El universo en su conjunto tiene una «velocidad de escape» análoga que determina si se sigue expandiendo eternamente o no. Los universos cerrados, que vuelven a colapsar sobre sí mismos, corresponden a la situación en que la velocidad de expansión es inferior a la velocidad de escape universal; los universos con curvatura negativa tienen una velocidad de expansión que supera su velocidad de escape. El universo de Einstein-De Sitter, con curvatura cero, se expande exactamente a la velocidad de escape, así que justo logra expandirse eternamente. Cualquier incremento en la densidad de la materia que contiene, por pequeño que sea, haría que la expansión fuese más lenta que su «velocidad de escape» y que el universo colapsase en el futuro.

El universo oscilante de Tolman

Todo lo que sube tiene que bajar.

Frederick A. Pottle^[113]

El trabajo pionero de Friedmann había hallado los primeros universos que se expanden hasta un tamaño máximo antes de contraerse de nuevo hasta un tamaño cero, como se muestra en la Figura 3.7. Friedmann había mencionado la posibilidad de que hubiese una secuencia continua de ciclos que pasasen por sucesivos máximos y mínimos de tamaño cero, como una pelota rebotando. Ya hemos hecho hincapié en que Friedmann no estaba muy interesado en la situación astronómica; su intención era simplemente hallar soluciones matemáticas a las ecuaciones de Einstein. Y sin embargo, se podían plantear cuestiones interesantes acerca de un escenario cosmológico en el que un universo cerrado oscilase para siempre desde un pasado hasta una eternidad futura. ¿Serían realmente iguales todos los ciclos, como en la Figura 3.17?

Esta cuestión fue abordada en 1932 por Richard Tolman en Cal Tech (Instituto Tecnológico de California), en Pasadena, California, una institución que Einstein visitaba con frecuencia. Los antecedentes científicos de Tolman eran bastante distintos a los de los otros pioneros de la cosmología. Tolman era profesor de química física y física matemática en Cal Tech, y estaba especialmente interesado en la termodinámica. Tolman consideró lo que sucedería si se aplicase la famosa segunda ley de la termodinámica a las soluciones de las ecuaciones de Einstein que describían un universo que oscilaba a lo largo de ciclos sucesivos (Figura 3.18). El aumento de la entropía de ciclo a ciclo sería como transformar energía de formas ordenadas, como átomos y galaxias, en desordenada radiación térmica. Es sencillo introducir este tipo de transferencia en las ecuaciones cosmológicas de Einstein, y significa que cada ciclo sucesivo de un universo oscilante contiene una fracción cada vez mayor de su energía en forma de radiación (que tiene una presión positiva) que su predecesor. Esto garantiza que el tamaño máximo de cada ciclo es mayor que el anterior (Figura 3.19). Las oscilaciones crecen en tamaño y edad total, y el universo acaba pareciéndose al de Einstein-De Sitter durante períodos de tiempo cada vez más prolongados hasta que deja de expandirse y colapsa.

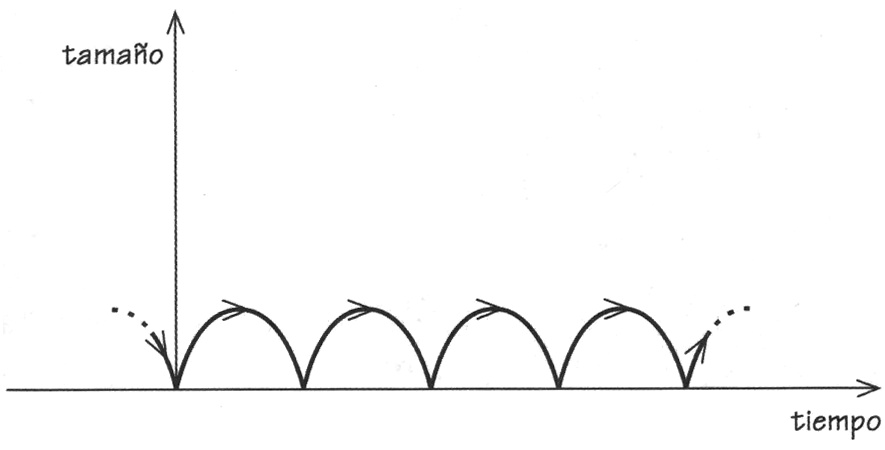
FIGURA 3.17. Un universo oscilante con ciclos idénticos en el que cada colapso hasta un big crunch va seguido por un nuevo ciclo de expansión, y así sucesivamente, para toda la eternidad. Este universo no tiene principio ni fin.

Si hacemos retroceder este universo en el tiempo, quizá no necesite un principio. En última instancia, si retrocedemos lo suficiente en el tiempo, debe de haber sido tan pequeño como para que los efectos cuánticos dominasen sobre la fuerza de gravedad, y quizá las ecuaciones de Einstein ya no fuesen válidas. También se podría afirmar que las ecuaciones de Einstein no son válidas hasta el tamaño cero del universo en cada rebote, porque en esos instantes la densidad de materia y radiación sería infinita. Sin embargo, si interviniese una nueva física cuántica gravitatoria para que el rebote tuviese lugar en un radio pequeño, pero no cero, aun podría tener lugar la misma secuencia de oscilaciones crecientes.

FIGURA 3.18. Richard Tolman explica la termodinámica de su escenario de universo oscilante a Einstein después de una conferencia. Las ecuaciones de la pizarra de atrás describen la termodinámica de la materia y la radiación en un universo en expansión.

Tolman era un científico cauteloso, y muchas de sus investigaciones sobre universos peculiares tenían el propósito de servir de advertencia a los que estuviesen tentados de sacar conclusiones prematuras sobre la naturaleza del universo. Así, la conclusión que extrae de este universo que rebota, de tamaño y entropía crecientes, es simplemente que:

Como mínimo parece más prudente no afirmar de forma dogmática que los principios de la termodinámica exigen necesariamente un universo creado un tiempo finito en el pasado, y condenado al estancamiento y la muerte en el futuro^[114].

Tolman pasó por alto un detalle interesante sobre este universo que rebota, que descubrimos Mariusz Dąbrowski y yo mismo mucho tiempo después, en 1995^[115]. Si se incluye la constante cosmológica repulsiva de Einstein, por pequeño que sea su valor, con el tiempo acabará con las oscilaciones y la expansión se acelerará hacia el comportamiento visto en el universo de De Sitter y nunca volverá a contraerse y oscilar (Figura 3.20^[116]).

FIGURA 3.19. El universo oscilante de Tolman. El aumento en la entropía total del universo y la conservación de su energía requieren que el tamaño máximo de los sucesivos ciclos aumente.

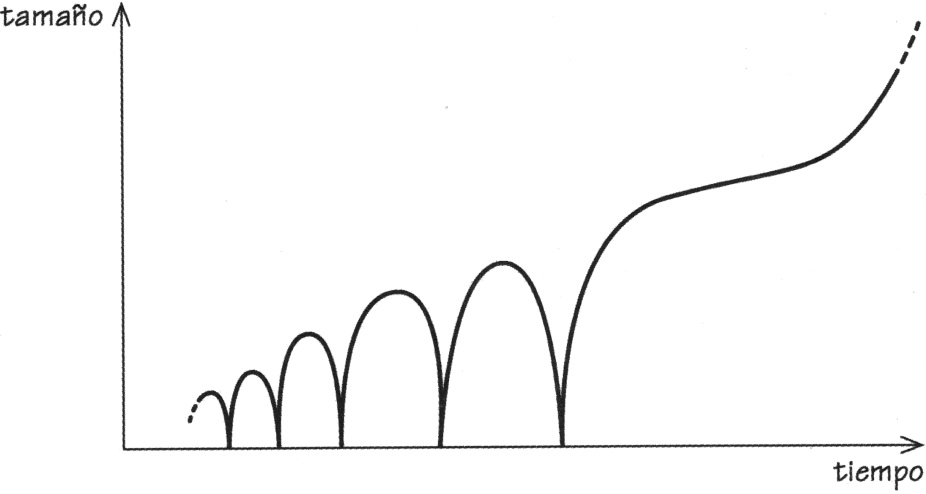
FIGURA 3.20. El universo del autor y Mariusz Dąbrowski tiene una fuerza lambda positiva. Por pequeño que sea el valor de lambda, las oscilaciones de Tolman terminarán por acabarse y entonces el universo se expandirá eternamente, pareciéndose cada vez más al universo de De Sitter.

El universo estrafalario de Lemaître y Tolman

W. H. Auden

En 1933, Lemaître y Tolman empezaron a evaluar la posibilidad de hallar universos matemáticos más realistas de los que se habían encontrado hasta ese momento. Siguiendo la estela de Einstein, los primeros intentos de hallar nuevos universos descritos por sus ecuaciones habían efectuado la hipótesis simplificadora de que el universo era igual en todas partes y en todas direcciones. El universo real no es así. Si lo fuera, no podríamos existir. Sin embargo, se esperaba que las desviaciones con respecto a la simetría perfecta fuesen lo bastante reducidas como para poder pasarlas por alto, al menos en un primer intento de describir el universo real. Pero al examinar el universo se ven irregularidades significativas, en forma de galaxias y estrellas repartidas por todo el cielo. ¿Podremos encontrar soluciones a las ecuaciones de Einstein que las tengan en cuenta?

Lemaître y Tolman consiguieron, por medios distintos, hallar los primeros universos no homogéneos, es decir, con propiedades —como la densidad de materia y el ritmo de expansión— que variaban de un lugar a otro y también en diferentes puntos temporales. El interés de Lemaître por este tipo de universo revelaba su visión de futuro. Se preguntó si podría ofrecer una forma de comprender por qué el universo contenía «bultos», como estrellas y galaxias. Sorprendentemente, es capaz de calcular el comportamiento de regiones más densas que la media, mostrando que se hacen más pronunciadas con el paso del tiempo (porque pueden atraer más material, a expensas de las regiones con una densidad menor que la media^[117]). Así, un universo con bultos contendrá cada vez más bultos a medida que se haga más viejo.

A Tolman, menos especulativo y audaz que Lemaître, le preocupaba extraer conclusiones demasiado tajantes sobre el universo a partir de hipótesis no verificables. En particular, todos los estudios sobre las ecuaciones de Einstein habían asumido hasta ese momento que el universo era igual en todas partes. Tolman pensaba que eso era bastante poco probable, de modo que las conclusiones sobre si el universo tuvo un principio, o sobre si colapsaría para desaparecer en algún momento del futuro, eran especulaciones más bien precarias. Se basaban en la pura hipótesis de que la parte del universo que no podíamos ver era igual que la que sí podíamos.

Cuando Tolman pudo encontrar soluciones a las ecuaciones de Einstein que describían universos irregulares simples, halló que permitían la existencia de universos en los que distintas partes se comportaban como distintas variedades de los universos de Friedmann-Lemaître. La curvatura del espacio y la densidad de materia podían variar suavemente de un lugar a otro. En una región, la densidad podía ser mayor que la media y la curvatura del espacio positiva: esa región se comportaría como un universo cerrado, expandiéndose hasta un tamaño máximo antes de colapsar de nuevo bajo su propia gravedad, quizá para formar una galaxia. En otra región, con una densidad inferior a la media, la curvatura sería negativa y la materia nunca podría superar la expansión y colapsar. Tolman sugiere que esto nos conduce a:

concebir la posibilidad de que haya regiones del universo que están más allá del alcance de nuestros actuales telescopios que pueden estar contrayéndose en lugar de expandirse, y que contienen materia con una densidad y en una etapa de desarrollo evolutivo muy distintas a aquellas con las que estamos familiarizados. Parece también sensato no sacar conclusiones definitivas del comportamiento de los modelos homogéneos en lo que se refiere al supuesto estado inicial del universo en su conjunto^[118].

Su prudencia en cuanto a no sacar conclusiones sobre el principio la motivaban tres características de estos universos estrafalarios permitidos por las ecuaciones de Einstein. En primer lugar, la variación de un lugar a otro significaba que el inicio de la expansión no tenía por qué ocurrir simultáneamente en todas partes. En segundo lugar, más adelante se apreció que podía incluso ocurrir una situación extrema en la que el principio en algunas partes del universo podía retrasarse tanto con respecto a otras que los que empezaron tarde podían ver y verse influenciados por las partes que empezaron primero^[119]. Finalmente, en situaciones en las que se incluía la constante cosmológica, podría haber algunas regiones en las que no hubiese principio (porque localmente se comportaban como el universo de Eddington-Lemaître), mientras que otras sí lo tuviesen.

Diferencias similares pueden surgir de un lugar a otro en lo que respecta al probable estado final del universo y la cuestión de si el universo es infinito o finito. Tolman señaló que podíamos estar viviendo en una gran región de gran densidad y curvatura positiva de un universo infinito que se expandirá eternamente, aunque la parte que podemos observar se comporte como un universo finito y cerrado que acabará por contraerse. Si asumiéramos que el universo en su conjunto tiene las mismas características que nuestra zona local, las conclusiones que sacaríamos acerca de sus propiedades globales serían totalmente erróneas.

El universo de Milne (y los universos de Newton)

No es posible detectar efecto alguno de la expansión (ningún factor de recesión, en concreto). Los datos disponibles siguen apoyando el modelo de un universo estático, no el de un universo en rápida expansión.

Edwin Hubble^[120]

A mediados de la década de 1930 se comprendían bastante bien los tipos simples de universo en expansión. Edwin Hubble había ampliado la provisión observacional de corrimientos hacia el rojo y ofrecía pruebas más sólidas de que la velocidad de recesión era proporcional a su distancia de nosotros. Hubble confirmó la primera deducción de Lemaître de la ley de Hubble en 1927, pero parecía reacio a aceptar que sus datos confirmaban la expansión del universo. El comportamiento general de las soluciones cosmológicas simples, homogéneas e isótropas de las ecuaciones de Einstein también se comprendía en profundidad. Esta comprensión fue generalizada a astrónomos menos inclinados a las matemáticas por el trabajo de dos cosmólogos ingleses, William McCrea (1904-1999) y Arthur Milne (1896-1950), que mostraron que el comportamiento de todos los universos hallados hasta entonces mediante la resolución del formidable sistema de ecuaciones de Einstein surge de forma más sencilla en la antigua teoría de la gravedad de Newton sin tener que utilizar en absoluto las ecuaciones de Einstein^[121]. Estos astrónomos describieron el comportamiento de una bola de materia en expansión sujeta a la famosa ley del cuadrado inverso de Newton. Si se desea incluir los efectos repulsivos de la constante cosmológica de Einstein, basta con agregar esta fuerza lambda adicional a la ley del cuadrado inverso de Newton para la fuerza gravitatoria entre dos masas. Los universos se expandían eternamente si su energía cinética era superior a la energía de la atracción gravitatoria entre las partículas de materia. Pero si la atracción gravitatoria salía vencedora, la expansión alcanzaría un máximo y se convertiría en contracción. Entre estas dos situaciones se hallaba el universo de Einstein y De Sitter, exactamente con una energía de expansión igual a la energía de atracción gravitatoria, como un cohete lanzado desde la Tierra exactamente a la «velocidad de escape» necesaria para huir del tirón gravitatorio del planeta. Esta forma de contemplar los universos más simples de Einstein sigue siendo la forma más habitual de enseñarlos a los estudiantes de física y astronomía.

Milne era un joven y brillante astrofísico que efectuó contribuciones clave a nuestra comprensión de las estrellas y sus atmósferas. Cuando consiguió una beca de entrada al Trinity College de Cambridge, lo hizo con las notas más altas que había recibido nunca ningún candidato. Se convirtió en Fellow de la Royal Society cuando aún no tenía treinta años, y lo nombraron profesor de Matemáticas en Oxford en 1928. Se empezó a interesar por la cosmología en 1932, y desarrolló una teoría propia del movimiento relativista; también cuestionó la idea ampliamente aceptada de la muerte térmica del universo.

Milne demostró que el universo en expansión y la ley de recesión de Hubble se podían comprender sin necesidad de la teoría de la gravedad de Einstein. Esto lo llevó a discutir si el «tiempo» que experimentan los átomos debe ser necesariamente el mismo que experimentan los sistemas «gravitatorios». Sin embargo, el nuevo tipo de universo en expansión que apoyaba se podía describir de forma muy simple mediante las ecuaciones de Einstein. El universo de Milne, como el de De Sitter, no contiene materia; pero, a diferencia de este, tampoco contiene la fuerza repulsiva de la constante cosmológica. Posee únicamente curvatura espacial negativa, y se expande eternamente a la velocidad de la luz (Figura 3.21^[122]).

El universo de Milne es el más simple posible con la hipótesis de que el universo es uniforme en el espacio e isótropo. Aunque suena especial y poco realista (después de todo, el universo real no está vacío de materia y radiación), su interés se ha mantenido porque, si se agrega materia y radiación a un universo abierto sin constante cosmológica, se expandirá eternamente y su comportamiento se hará cada vez más próximo al del universo de Milne^[123].

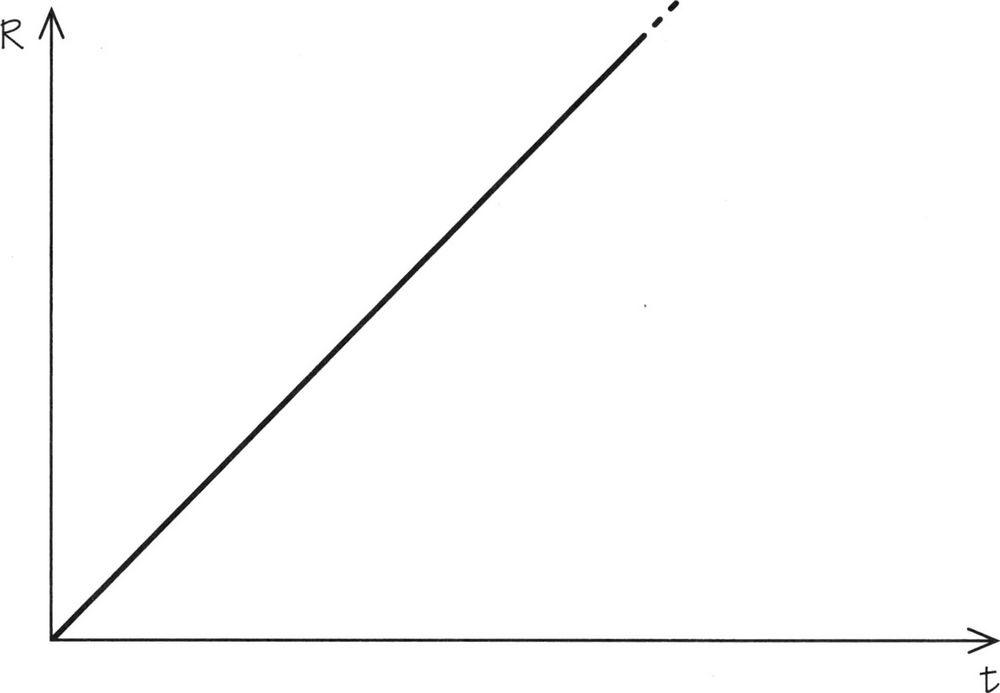
FIGURA 3.21. Universo de Milne. Las distancias aumentan en proporción directa a la edad del universo.

Milne era un científico con firmes creencias y motivaciones religiosas (anglicanas), y estaba interesado en conciliar la imagen científica de un universo en expansión con la concepción cristiana de Dios y el universo creado. Escribió mucho sobre esta cuestión, en particular su libro Modern Cosmology and the Christian Idea of God^[124] (Cosmología moderna y la idea cristiana de Dios), publicado póstumamente^[125] en 1952. Sin embargo, nunca escribió para el público en general, y sus libros son solo fácilmente accesibles para físicos y matemáticos. Desarrolló una acentuada preferencia por un universo infinito, porque ofrecía el ámbito perfecto para que la Deidad llevara a cabo un número ilimitado de experimentos evolutivos. Para él, un universo finito limitaba el alcance de la acción divina.

La cosmología matemática de Milne intentaba deducir la única estructura «racional» posible para la geometría del universo, y creía que esta estructura racional imponía algunas restricciones sobre el tipo de universo que Dios podía haber creado. Según creía, el universo no se podía expandir a velocidades diferentes en distintas direcciones; aunque, como veremos en el próximo capítulo, otros estaban en desacuerdo con él acerca de esta cuestión. Debía tener leyes universales, iguales en todas partes, porque él sostenía que las leyes de la Naturaleza eran determinadas racionalmente por la estructura del universo: la ley de la gravedad no podía modificarse ni un ápice sin destruir la armonía de todo el cosmos. Así, para Milne, Dios sufría hasta cierto punto las restricciones de la lógica, que dictaba la forma del universo y las leyes que podía aceptar^[126]. No obstante, esta condición quedaba equilibrada por la infinitud del espacio: Milne creía que todas las posibilidades biológicas podían tener lugar en ese cosmos infinito. Curiosamente, esta forma de pensar acerca de estas cuestiones era totalmente opuesta a la de Lemaître. Milne estaba muy apegado a la finitud del universo. Para él, el universo estaba aquí para que los seres vivos los explorasen y lo comprendiesen. Un universo infinito lo hacía imposible: era mayor que la comprensión humana; cualquier cosa podía suceder en algún lugar: era un hogar demasiado grande para sus habitantes.