VII
Il primo centesimo di secondo
Nel capitolo V, raccontando i primi tre minuti dell’universo, non cominciammo dal principio. Il lettore ricorderà che ini-ziammo il nostro film con un « primo fotogramma » corrispondente a una fase in cui la temperatura cosmica era già scesa a 100 miliardi di gradi Kelvin e in cui le sole particelle presenti in gran numero erano fotoni, elettroni, neutrini e le rispettive antiparticelle. Se questi erano veramente gli unici tipi di particelle esistenti in natura, potremmo forse estrapolarne l’espansione dell’universo a ritroso nel tempo, e inferire che dev’esserci stato un autentico principio, uno stato di temperatura e densità infinite, che possiamo collocare 0,0108 secondi prima del nostro primo fotogramma.
La fìsica moderna conosce però molti altri tipi di particelle: muoni, pioni, protoni, neutroni, e così via. Quando volgiamo il nostro sguardo a tempi sempre più remoti, ci imbattiamo in temperature e densità così elevate che tutte queste particelle devono essere state presenti, in quantità enormi, in condizioni di equilibrio termico e tutte quante in uno stato di continua interazione reciproca. Per ragioni che spero di poter chiarire, n o i non sappiamo ancora sulla fisica delle particelle nucleari quanto basta per calcolare con una certa sicurezza le proprietà di un simile miscuglio. Così la nostra ignoranza della fisica 150 I primi tre minuti
microscopica fa velo alla nostra visione dell’istante iniziale.
Naturalmente la prospettiva di sbirciare dietro quel velo ci tenta. La tentazione è particolarmente forte per teorici come me, per coloro che hanno lavorato più nel campo delle particelle elementari che non in quello dell’astrofisica. Molte interessanti concezioni dell’odierna fisica delle particelle hanno conseguenze così sottili che risulta estremamente difficile verificar-le in laboratorio, ma si tratta di conseguenze addirittura cla-morose quando tali concezioni vengono applicate ai primissimi istanti della storia dell’universo.
Il primo problema che ci troviamo ad affrontare quando il nostro sguardo si volge a considerare temperature superiori a 100 milioni di gradi ci viene proposto dalle « interazioni forti »
delle particelle elementari. Le interazioni forti sono le forze che tengono insieme in un nucleo atomico neutroni e protoni.
A differenza delle forze elettromagnetiche e gravitazionali, queste forze non ci sono familiari nella vita quotidiana, perché il loro raggio d’azione è estremamente breve, di circa un decibi-lionesimo di centimetro (10-13 cm). Anche nelle molecole, in cui i nuclei atomici distano fra loro, tipicamente, di intervalli dell’ordine di alcuni centomilionesimi di centimetro (10-8 cm), le interazioni forti fra nuclei diversi non hanno virtualmente effetto. Tuttavia, come indica il loro nome, le interazioni forti sono molto forti. Quando due protoni vengono sospinti abbastanza vicini l’uno all’altro, l’interazione forte fra loro diventa circa 100 volte maggiore della repulsione elettrica; perciò le interazioni forti sono in grado di dare coesione ai nuclei atomici di contro alla repulsione elettrica di quasi 100 protoni.
L’esplosione di una bomba H è causata da una ridisposizione di neutroni e protoni che a questi consente di essere legati in modo più compatto ed efficace a opera delle interazioni forti; l’energia della bomba è esattamente l’eccesso di energia reso disponibile dal nuovo assetto.
Proprio alla forza eccezionale delle interazioni forti si deve
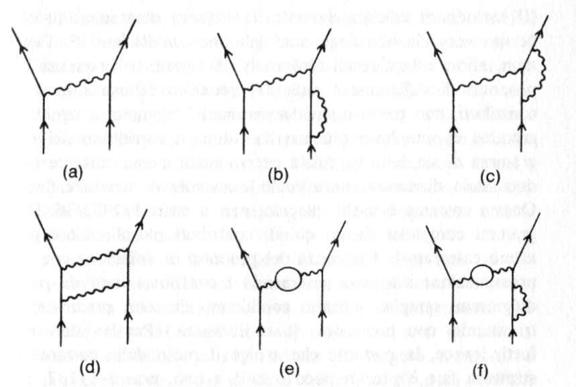
Figura 10. Alcuni diagrammi di Feynman. La figura propone alcuni fra i più semplici diagrammi di Feynman per il processo di diffusione elettrone-elettrone.
Le linee rette designano elettroni o positoni; le linee ondulate designano fotoni.
Ogni diagramma rappresenta una certa quantità numerica dipendente dalle quantità di moto e dagli spin degli elettroni in ingresso e in uscita; la frequenza del processo di diffusione è uguale al quadrato della somma di queste quantità, associate a tutti i diagrammi di Feynman. Il contributo di ogni diagramma a questa somma è proporzionale a un numero di fattori di 1/137 (la costante di struttura fine) dato dal numero di linee fotoniche. 11 diagramma (a) rappresenta lo scambio di un singolo fotone e costituisce il contributo principale, proporzionale a 1/137. I diagrammi (b), (c), (d), (e) rappresentano tutti i tipi di diagrammi che formano le correzioni « radiative » dominanti ad (a), e costituiscono tutti contributi dell’ordine (1/137)2. Il diagramma (f) costituisce un contributo ancora più piccolo, proporzionale a (1/137)3.
se il loro trattamento matematico è assai più difficile di quello delle interazioni elettromagnetiche. Quando, per esempio, cal-coliamo la frequenza di diffusione di due elettroni dovuta alla repulsione elettromagnetica esistente fra loro, dobbiamo som-mare un numero infinito di contributi corrispondenti ciascuno a una particolare sequenza di emissione e di assorbimento di fotoni e di coppie elettroni-positoni, simboleggiati in un « diagramma di Feynman » come quelli illustrati nella figura 10.
152 I primi tre minuti
(Il metodo di calcolo che ricorre a questi diagrammi fu ela-borato verso la fine degli anni quaranta da Richard P. Feynman, allora alla Cornell University. A rigore, la frequenza del processo di diffusione è data dal quadrato di una somma di contributi, uno per ciascun diagramma.) L’aggiunta a ogni diagramma di una linea più interna riduce il contributo del diagramma di un fattore press’a poco uguale a una costante fondamentale di natura, nota come « costante di struttura fine ».
Questa costante è molto piccola, pari a circa 1 / 1 3 7 , 0 3 6 . Diagrammi complessi danno quindi contributi piccoli, e noi possiamo calcolare la frequenza del processo di diffusione con approssimazione adeguata sommando i contributi tratti da pochi diagrammi semplici. (Perciò confidiamo di poter predire spettri atomici con precisione quasi illimitata.) Per le interazioni forti, invece, la costante che svolge il ruolo della costante di struttura fine è press’a poco uguale a uno, non a 1 / 1 3 7 , per cui i diagrammi complicati danno un contributo altrettanto grande quanto i diagrammi semplici. Questo problema, ossia la difficoltà di calcolare frequenze per processi implicanti interazioni forti, ha rappresentato il massimo ostacolo singolo al progresso nella fisica delle particelle elementari relativamente all’ultimo quarto di secolo.
N o n tutti i processi comportano interazioni forti. Le interazioni forti operano infatti solo all’interno di una classe di particelle conosciute come « adroni » (dal greco hadros, « forte »).
Questa classe comprende le particelle nucleari, i pioni e altre particelle instabili, denominate kaoni, mesoni eta, iperoni lambda, iperoni sigma, ecc. Gli adroni sono generalmente più pesanti, hanno cioè massa maggiore, dei leptoni (il vocabolo « leptoni » deriva dalla parola greca leptos, che significa « leggero »), ma la differenza veramente importante che intercorre fra queste categorie consiste nel fatto che gli adroni, diversamente dai leptoni - i neutrini, gli elettroni e i muoni -, soggiacciono agli effetti delle interazioni forti. Il fatto che gli