I primi tre minuti

di Einstein. Per esempio, la regola abituale per la somma delle velocità ci dice che se un passeggero, su un aereo che volasse a una velocità pari a tre quarti della velocità della luce, sparas-se in avanti un proiettile la cui velocità fosse anch’essa pari a tre quarti della velocità della luce, la velocità del proiettile rispetto al suolo risulterebbe pari a una volta e mezzo la velocità della luce, il che è impossibile. La relatività speciale evita questo problema modificando la regola per la somma delle velocità: la velocità di C rispetto ad A è in realtà un po’

minore della somma delle velocità di B relativamente ad A e di C relativamente a B, secondo una formula tale che, per quante velocità inferiori a quella della luce noi sommiamo, non otterremo mai una velocità superiore a quella della luce.

Nessuno di questi problemi esisteva per Hubble nel 1929; nessuna delle galassie da lui studiate allora aveva una velocità prossima a quella della luce. Oggi, invece, quando i cosmologi meditano sulle smisurate distanze caratteristiche dell’universo nel suo complesso, devono operare in una cornice teorica in grado di ammettere velocità che si approssimano a quella della luce, devono cioè tenere conto delle teorie della relatività di Einstein, speciale (o ristretta) e generale. Di fatto, quando ci occupiamo di distanze di tale grandezza, il concetto stesso di distanza diventa ambiguo, e noi dobbiamo specificare se intendiamo la distanza misurata dall’osservazione di luminosità o di diametri o di moti propri o di qualcos’altro.

Tornando al 1929: Hubble stimò la distanza di 18 galassie sulla base della luminosità apparente delle loro stelle più brillanti e confrontò queste distanze con le velocità rispettive delle galassie, determinate spettroscopicamente sulla base dei loro spostamenti Doppler. In seguito a quest’esame concluse che esisteva « una relazione pressoché lineare » (cioè una proporzionalità semplice) fra velocità e distanze. In realtà, dopo una occhiata ai dati di Hubble, mi chiesi perplesso come avesse potuto raggiungere una simile conclusione: le velocità galattiche L’espansione dell’universo 37

sembrano prive di qualsiasi rapporto con le distanze, se si prescinde da una lieve tendenza a un aumento della velocità con la distanza. In verità non dovremmo attenderci alcuna precisa relazione di proporzionalità fra velocità e distanza per queste 18 galassie: sono tutte troppo vicine, nessuna di esse trovan-dosi oltre l’ammasso della Vergine. È difficile evitare di dedurre che, fondandosi o sui ragionamenti semplici esposti sopra o sugli sviluppi teorici a essi collegati che esamineremo più avanti, Hubble conoscesse già la risposta che si proponeva di ottenere.

In ogni caso, nel 1931 i materiali d’osservazione si erano accumulati in misura notevole e Hubble fu in grado di verificare la proporzionalità fra velocità e distanza per galassie le cui velocità raggiungevano i 20 0 0 0 chilometri al secondo. Con le stime di distanze allora disponibili, la conclusione fu che le velocità aumentano di 170 chilometri al secondo ogni milione di anni-luce di distanza; una velocità di 20 0 0 0 chilometri al secondo significa pertanto una distanza di 120 milioni di anni-luce. Questa cifra, che indica un certo aumento di velocità in relazione alla distanza, è nota generalmente come « costante di Hubble ». (Si tratta di una costante nel senso che la proporzionalità fra velocità e distanza è la stessa per tutte le galassie in un dato tempo; ma, come vedremo, la costante di Hubble muta col tempo man mano che l’universo si evolve.) Nel 1936 Hubble, in collaborazione con lo spettroscopista Milton Humason, riuscì a misurare la distanza e la velocità dell’ammasso di galassie Ursa Maior II. Trovò che tale ammasso stava allontanandosi a una velocità di 42 0 0 0 chilometri al secondo (il 14 per cento della velocità della luce). La distanza, stimata allora a 2 6 0 milioni di anni-luce, era al limite della potenza dello strumento di Monte Wilson, e il lavoro di Hubble dovette fermarsi qui. D o p o la guerra, con l’avvento di telescopi più potenti negli osservatori di Palomar e Monte Hamilton, il programma di Hubble fu ripreso da altri astro-38 I primi tre minuti

nomi (segnatamente da Alian Sandage, degli osservatori di Palomar e di Monte Wilson) e continua tuttora.

La conclusione che viene generalmente tratta da questo

mezzo secolo di osservazioni è che le galassie stanno allontanandosi da noi, con velocità proporzionali alla distanza (almeno finché si tratta di velocità non troppo vicine a quella della luce). Ovviamente, come abbiamo già sottolineato nella nostra discussione del Principio cosmologico, ciò non significa che noi ci troviamo in una posizione del cosmo particolarmente favorevole o sfavorevole; ogni galassia si sta allontanando da ogni altra galassia con una velocità relativa proporzionale alla reciproca distanza. La modifica più importante ap-portata alle conclusioni originali di Hubble è una revisione della scala delle distanze extragalattiche: in parte per effetto di una correzione, operata da Walter Baade e altri, della relazione periodo-luminosità delle cefeidi determinata dalla Leavitt e da Shapley, le distanze delle galassie più lontane sono stima-te oggi circa dieci volte maggiori di quanto non si pensasse al tempo di Hubble. Il valore della costante di Hubble oggi accettato è così sceso a soli 15 chilometri al secondo per ogni milione di anni-luce.

Che cosa ci dice tutto ciò a proposito dell’origine dell’universo? Se le galassie stanno allontanandosi l’una dall’altra, in passato devono essersi trovate molto più vicine. Per la precisione, se la loro velocità è stata costante, allora il tempo impiegato da due galassie scelte a piacere per venirsi a trovare separate dalla distanza attuale è esattamente uguale alla distanza attuale divisa per la loro velocità relativa. Ma con una velocità proporzionale alla distanza attuale, questo tempo risulta identico per ogni coppia di galassie scelte a piacere: in passato, esse devono essersi trovate tutte molto vicine nello stesso tempo. Fissando la costante di Hubble in 15 chilometri al secondo per milione di anni-luce, il tempo trascorso da quando le galassie hanno cominciato ad allontanarsi l’una dall’al-L’espansione dell’universo 39

tra sarebbe un milione di anni-luce diviso per 15 chilometri al secondo, ossia 20 miliardi di anni. Ci riferiremo all’« età »

calcolata in questo modo come al « tempo di espansione caratteristico »: semplicemente, l’inverso della costante di Hubble. La vera età dell’universo è di fatto minore del tempo di espansione caratteristico perché, come vedremo, le galassie non si sono mosse con velocità costante ma con una velocità lentamente decrescente in conseguenza della reciproca gravitazione. Perciò, se la costante di Hubble è di 15 chilometri al secondo per ogni milione di anni-luce di distanza, l’età del l’universo dev’essere inferiore a 20 miliardi di anni.

A volte riassumiamo queste nozioni dicendo in sintesi che le dimensioni dell’universo stanno aumentando. Ciò non significa necessariamente che l’universo abbia dimensioni finite, anche se può essere così. Usiamo questo linguaggio perché in ogni intervallo di tempo dato la distanza fra due galassie tipiche scelte a piacere aumenta di una stessa quantità frazionaria.

Durante ogni intervallo abbastanza breve perché le velocità delle galassie rimangano approssimativamente costanti, l’aumento della distanza fra due galassie tipiche scelte a piacere sarà dato dal prodotto della loro velocità relativa per il tempo trascorso; ovvero, applicando la legge di Hubble, dal prodotto della costante di Hubble per la distanza per il tempo. Ma allora il rap-

porto fra l’aumento della distanza e la distanza stessa sarà dato dal prodotto della costante di Hubble per il tempo trascorso, prodotto che è uguale per ogni coppia di galassie scelte a piacere. Per esempio, durante un intervallo di tempo pari all‘1 per cento del tempo di espansione caratteristico (che è, come abbiamo visto, l’inverso della costante di Hubble), la distanza fra due galassie qualsiasi aumenterà dell‘1 per cento.

Diremo allora, in termini non rigorosi, che le dimensioni dell’universo si sono accresciute dell‘1 per cento.

N o n vorrei suscitare l’impressione che tutti siano d’accordo con questa interpretazione dello spostamento verso il rosso.

40 I primi tre minuti

In realtà, non osserviamo galassie che si stanno allontanando da noi a velocità vertiginose; tutto ciò di cui siamo certi è che le righe dei loro spettri sono spostate verso il rosso, verso lunghezze d’onda maggiori. Ci sono eminenti astronomi i quali dubitano che gli spostamenti verso il rosso abbiano veramente a che fare con l’effetto Doppler o con un’espansione dell’universo. Halton Arp, degli Hale Observatories, ha messo in ri-salto l’esistenza di raggruppamenti di galassie in cui alcune galassie presentano spostamenti verso il rosso molto diversi da quelli di altre; se tali raggruppamenti costituiscono autentiche associazioni fisiche di galassie vicine, difficilmente queste potrebbero avere velocità molto diverse. Nel 1963, inoltre, Maarten Schmidt scoprì che una certa classe di oggetti che hanno l’aspetto di stelle presentano tuttavia spostamenti verso il rosso enormi, in qualche caso di oltre il 300 per cento! Se questi « oggetti quasi stellari » sono così lontani come indicano gli spostamenti verso il rosso delle loro righe spettrali, dovrebbero emettere quantità di energia enormi per essere così brillanti. Infine, non è facile determinare il rapporto fra velocità e distanza a distanze realmente grandi.

Esiste però un procedimento indipendente per confermare che le galassie stanno allontanandosi le une dalle altre, come suggeriscono gli spostamenti verso il rosso. Come abbiamo visto, questa interpretazione degli spostamenti verso il rosso implica che l’espansione dell’universo abbia avuto inizio un po’ meno di 20 miliardi di anni or sono. Essa risulterà perciò in qualche misura confermata se riusciremo a trovare altre prove del fatto che l’universo è effettivamente così antico. Di fatto esistono buoni motivi per supporre che la nostra galassia abbia una età di circa 10-15 miliardi di anni. Questa stima deriva sia dall’abbondanza relativa di vari isotopi radioattivi sulla Terra (specialmente gli isotopi dell’uranio U 235 e U 238) sia dal calcolo dell’evoluzione delle stelle. Ora, dal momento che fra i ritmi della radioattività o dell’evoluzione stellare e lo spo-L’espansione dell’universo 41

stamento verso il rosso delle galassie lontane non esiste sicuramente alcuna connessione diretta, acquista credibilità la supposizione che l’età dell’universo dedotta dalla costante di Hubble rappresenti un autentico inizio.

In proposito è storicamente interessante ricordare che fra il 1930 e il 1950 si attribuiva alla costante di Hubble un valore di circa 170 chilometri al secondo per ogni milione di anni-luce di distanza, molto più elevato del valore attuale. In virtù del nostro ragionamento precedente, l’età dell’universo sarebbe risultata pari a un milione di anni-luce diviso per 170 chilometri al secondo, cioè a circa due miliardi di anni, o anche meno tenendo conto del rallentamento gravitazionale. Ma fin dall’epoca degli studi di Lord Rutherford sulla radioattività è noto che la Terra ha un’età molto superiore a questa stima; oggi si ritiene che abbia circa 4,6 miliardi di anni. N o n si può certo pensare che la Terra sia più vecchia dell’universo; gli astronomi furono perciò indotti a dubitare che lo spostamento verso il rosso sia veramente indicativo dell’età dell’universo.

Alcune fra le idee cosmologiche più geniali del periodo 1930-1950 nacquero sotto lo stimolo di questo paradosso apparente, compresa forse la teoria dello stato stazionario. Può darsi che la rimozione del paradosso dell’età in seguito alla decuplica-zione della scala delle distanze extragalattiche negli anni cinquanta sia stata un presupposto essenziale per l’emergere della cosmologia del big bang come teoria standard.

L’immagine dell’universo che siamo venuti delineando è

quella di uno sciame di galassie in espansione. La luce non ha svolto finora per noi altro ruolo se non quello di « nunzio si-dereo », portandoci informazioni sulla distanza e la velocità delle galassie. Alle origini dell’universo la situazione era però molto diversa; come vedremo, era la luce a costituire l’ingrediente dominante dell’universo, e la comune materia non era altro che una trascurabile contaminazione. Converrà quindi riformulare più oltre quanto abbiamo appreso sugli spostamen-42 I primi tre minuti

ti verso il rosso in relazione al comportamento delle onde luminose in un universo in espansione.

Consideriamo un’onda luminosa in movimento fra due galassie tipiche. La distanza fra le galassie è uguale al prodotto del tempo impiegato dalla luce per percorrerla moltiplicato per la velocità della luce, mentre l’aumento di tale distanza durante il viaggio della luce da una galassia all’altra è uguale al prodotto del tempo impiegato dalla luce nel suo viaggio moltiplicato per la velocità relativa delle galassie. Quando calco-liamo l’aumento frazionario della distanza, dividiamo l’aumento della distanza per il valore medio di questa distanza durante l’aumento, e troviamo che il tempo impiegato dalla luce a compiere il suo viaggio viene eliminato: l’aumento frazionario nella distanza di queste due galassie (e quindi di qualsiasi altra coppia di galassie tipiche) durante il tempo impiegato dalla luce per viaggiare da una galassia all’altra è esattamente uguale al rapporto fra la velocità relativa delle galassie e la velocità della luce. Ma, come abbiamo già visto, questo stesso rapporto ci dà anche l’aumento frazionario della lunghezza d’onda della luce durante il suo viaggio. Ne desumiamo che la lunghezza

d’onda di ogni raggio di luce aumenta semplicemente in pro-

porzione all’aumento della distanza fra galassie tipiche in con-

seguenza dell’espandersi dell’universo. Possiamo pensare che le creste d’onda vengano sempre più « separate » dall’espansione dell’universo. Benché il nostro ragionamento sia stato valido, a rigore, solo per percorsi relativamente brevi, se componiamo una sequenza di questi percorsi parziali della luce possiamo concludere che esso conserva la sua validità anche su un piano più generale. Per esempio, se consideriamo la galassia 3C 295

e osserviamo che le lunghezze d’onda nei suoi spettri sono maggiori del 46 per cento rispetto alle nostre tavole standard delle lunghezze d’onda spettrali, possiamo inferirne che, quando la luce venne emessa, l’universo era del 46 per cento più piccolo di quanto non sia oggi.

L’espansione dell’universo 43

Finora ci siamo occupati di problemi che i fisici designano come « cinematici », di problemi, cioè, che hanno a che fare con la descrizione del moto indipendentemente da ogni consi-derazione delle forze che lo governano. Per secoli, fisici e astronomi hanno però tentato anche di capire la dinamica dell’universo. Questi tentativi hanno condotto inevitabilmente al-lo studio della funzione cosmologica dell’unica forza che agisce fra corpi astronomici: la forza di gravitazione.

Com’era lecito attendersi, fu Isaac Newton il primo ad affrontare il problema. In un famoso carteggio col classicista di Cambridge Richard Bentley, Newton ammise che, se la materia dell’universo fosse distribuita in modo uniforme in una regione finita, tenderebbe a cadere tutta verso il centro, « e a comporre ivi una grande massa sferica ». Al contrario, se la materia fosse dispersa in modo uniforme attraverso uno spazio

infinito, non ci sarebbe alcun centro verso cui potrebbe cadere.

In tal caso potrebbe contrarsi dando origine a un numero infinito di masse materiali disseminate nell’universo; questa, secondo Newton, la possibile origine del Sole e delle stelle.

La difficoltà di occuparsi della dinamica di un mezzo infinito paralizzò praticamente ogni ulteriore progresso fino al-l’avvento della relatività generale. Non è questa la sede per una spiegazione di tale teoria; del resto essa si rivelò, per la cosmologia, meno importante di quanto non si pensasse ini-zialmente. Ci limitiamo a ricordare che Albert Einstein si servì della già esistente teoria matematica delle geometrie non euclidee per spiegare la gravitazione come un effetto della curvatura dello spazio e del tempo. Nel 1917, un anno dopo il completamento della sua teoria generale della relatività, Einstein cercò di trovare una soluzione delle sue equazioni che descrivesse la geometria spaziotemporale dell’intero universo.

Ispirandosi ai concetti cosmologici allora correnti, Einstein ri-cercava specificamente una soluzione che fosse omogenea, isotropa e, purtroppo, statica. Ma non riuscì a trovare alcuna 44 I primi tre minuti

soluzione del genere. Tendendo a un modello conforme a questi presupposti cosmologici, Einstein fu costretto a storpiare le sue equazioni introducendo un termine, la cosiddetta « costante cosmologica », che sfigurava gravemente l’eleganza della teoria originaria, ma che poteva servire a controbilanciare la attrazione gravitazionale a grandi distanze.

Il modello dell’universo di Einstein era veramente statico e non prevedeva alcuno spostamento verso il rosso. Nello stesso 1917 un’altra soluzione della teoria modificata di Einstein venne elaborata dall’astronomo olandese W. de Sitter. Benché ap-parisse statica, e fosse perciò accettabile in accordo con le idee cosmologiche del tempo, questa soluzione aveva la notevole caratteristica di prevedere uno spostamento verso il rosso proporzionale alla distanza! L’esistenza di grandi spostamenti verso il rosso negli spettri delle nebulose era allora sconosciuta agli astronomi europei. Al termine della Prima Guerra M o n -

diale la notizia dell’osservazione di grandi spostamenti nebu-lari verso il rosso arrivò in Europa dall’America, e il modello di de Sitter acquistò un’immediata celebrità. Nel 1922, scrivendo il primo vasto trattato sulla relatività generale, l’astronomo inglese Arthur Eddington analizzò i dati disponibili degli spostamenti verso il rosso in riferimento al modello di de Sitter.

Lo stesso Hubble disse che era stato il modello di de Sitter ad attirare l’attenzione degli astronomi sull’importanza di una dipendenza dello spostamento verso il rosso dalla distanza; questo modello potrebbe anzi avere influito, sia pure inconscia-mente, sulla sua stessa scoperta della proporzionalità dello spostamento verso il rosso alla distanza (1929).

Oggi questo rilievo accordato al modello di de Sitter appare in gran parte ingiustificato. Da un lato, non si tratta affatto di un modello statico: sembrava statico a causa del modo peculiare in cui vi erano state introdotte le coordinate spaziali, ma di fatto nel modello la distanza fra osservatori « tipici » aumenta col tempo, ed è questa recessione generale a produrre L’espansione dell’universo 45

lo spostamento verso il rosso. Inoltre la ragione per cui nel modello di de Sitter lo spostamento verso il rosso risultava proporzionale alla distanza consiste appunto nel fatto che tale modello soddisfa il Principio cosmologico e, come abbiamo visto, ci attendiamo una proporzionalità fra velocità relativa e distanza in ogni teoria che soddisfi questo principio.

In ogni caso, la scoperta della recessione di galassie lontane suscitò ben presto un grande interesse per modelli cosmologici omogenei e isotropi ma non statici. N o n c’era nessun bisogno di una « costante cosmologica » nelle equazioni di campo della gravitazione, e Einstein si rammaricò di aver considerato la possibilità di introdurre un tale mutamento nelle sue equazioni originali. Nel 1922 la soluzione generale omogenea e isotropa delle equazioni originali di Einstein fu trovata dal matematico russo Aleksandr A. Friedmann. Sono questi modelli di Fried mann, fondati sulle equazioni di campo originarie di Einstein, e non i modelli di Einstein o di de Sitter, a fornire la base matematica alla maggior parte delle teorie cosmologiche moderne.

I modelli di Friedmann sono di due tipi molto diversi. Se la densità media della materia dell’universo è minore o uguale rispetto a un certo valore critico, allora l’universo dev’essere spazialmente infinito. In questo caso la presente espansione dell’universo durerà per sempre. Se invece la densità dell’universo è maggiore di tale valore critico, allora il campo gravitazionale prodotto dalla materia incurva l’universo su se stesso; l’universo è finito benché illimitato, come la superficie di una sfera (in altri termini, se noi iniziamo un viaggio in linea retta non raggiungeremo mai i confini dell’universo ma torneremo al punto di partenza). In questo caso i campi gravitazionali sono abbastanza intensi per mettere fine col tempo alla espansione dell’universo; a questo punto si avrà il fenomeno inverso della contrazione (implosione), fino a raggiungere una densità indefinitamente grande. La densità critica è proporzio-46 I primi tre minuti

nale al quadrato della costante di Hubble; per /valore attualmente accettato di 15 chilometri al secondo per ogni milione di anni-luce la densità critica è uguale a 5 x 1030 grammi per centimetro cubico, il che equivale a tre atomi di idrogeno ogni mille litri di spazio.

Il moto di ogni galassia tipica nei modelli di Friedmann corrisponde esattamente a quello di un sasso lanciato verso l’alto dalla superficie della Terra. Se il sasso viene scagliato con una velocità sufficiente o, che è lo stesso, se la massa della Terra è abbastanza piccola, la pietra rallenterà gradualmente il suo moto ma riuscirà comunque a sfuggire all’attrazione terrestre fino a perdersi nell’infinito. Questo esempio corrisponde al caso di una densità cosmica inferiore alla densità critica.

Se il sasso viene scagliato verso l’alto con velocità insufficiente, raggiungerà una certa altezza e poi ricadrà. Questo secondo esempio corrisponde al caso di una densità cosmica superiore alla densità critica.

Questa analogia chiarisce perché non era stato possibile trovare soluzioni cosmologiche statiche alle equazioni di Einstein: non ci stupiamo più di tanto se vediamo una pietra muoversi verso l’alto o verso il basso rispetto alla superficie della Terra, ma sicuramente non ci aspetteremmo di vederne una sospesa immobile a mezz’aria. L’analogia ci aiuta anche a evitare un fraintendimento comune a proposito dell’universo in espansione. Le galassie non si stanno allontanando l’una dall’altra a causa di qualche forza misteriosa che le sospinga, così come il sasso che si eleva non è certo respinto dalla Terra. Le galassie stanno allontanandosi reciprocamente perché hanno ricevuto un impulso da qualche esplosione avvenuta in passato.

Anche se la cosa non veniva rilevata negli anni venti, molte delle singole proprietà dei modelli di Friedmann possono essere calcolate quantitativamente mediante questa analogia, senza alcun riferimento alla relatività generale. Al fine di calcolare il moto di una qualsiasi galassia tipica rispetto alla nostra, trac-L’espansione dell’universo 47

ciamo una sfera con noi al centro e la galassia in questione alla superficie; il moto di questa galassia è precisamente quale sarebbe se la massa dell’universo constasse solo della materia contenuta in questa sfera e se all’esterno di essa non ci fosse niente. È come se noi scavassimo una profonda caverna nell’interno della Terra e osservassimo il modo in cui cadono i corpi: troveremmo che l’accelerazione gravitazionale verso il centro dipende solo dalla quantità di materia che si trova fra la nostra caverna e il centro, come se la superficie della Terra venisse a trovarsi in corrispondenza col fondo della nostra caverna. Questo notevole risultato è espresso da un teorema, valido sia nella teoria gravitazionale di Newton sia in quella di Einstein, che dipende solo dalla simmetria sferica del sistema studiato; la versione di questo teorema nell’ambito della relatività generale fu dimostrata dal matematico americano G.

D. Birkhoff nel 1923, ma per qualche decennio non ci si rese conto del suo significato cosmologico.

Possiamo servirci di questo teorema per calcolare la densità critica dei modelli di Friedmann (cfr. fig. 3). Quando tracciamo una sfera con noi al centro e una qualche galassia remota alla superficie, possiamo usare la massa delle galassie comprese all’interno della sfera per calcolare una velocità di fuga, la velocità che una galassia alla superficie di tale sfera dovrebbe avere per evadere nell’infinito. Risulta che questa velocità di fuga è proporzionale al raggio della sfera: quanto più grande è la sfera, tanto maggiore dev’essere la velocità per potersi sot-trarre alla sua attrazione. Ma la legge di Hubble ci dice che anche la velocità di una galassia alla superficie della sfera è proporzionale al raggio della sfera: alla distanza da noi. Così, benché la velocità di fuga dipenda dal raggio, il rapporto della velocità reale della galassia alla sua velocità di fuga non dipende dalle dimensioni della sfera, bensì è uguale per tutte le galassie, qualunque sia la galassia che poniamo al centro della sfera. In dipendenza dai valori della costante di Hubble e della

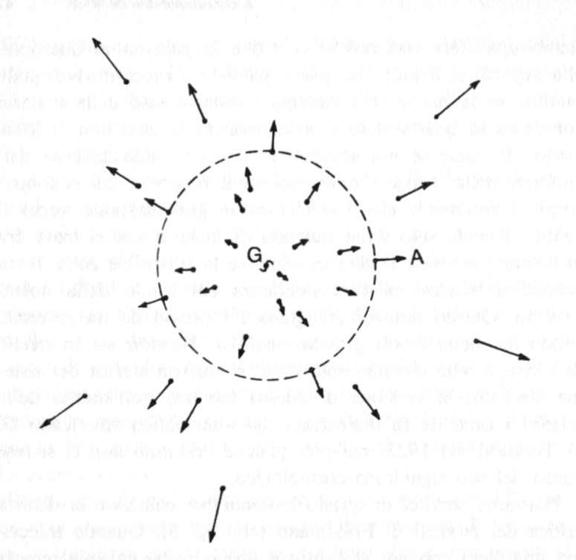
Figura 3. Il teorema di Birkhoff e l’espansione dell’universo. La figura presenta alcune galassie, le cui velocità relative rispetto a una galassia data G s o n o indicate dalla lunghezza e dalla direzione delle rispettive frecce. (In a c c o r d o con la legge di Hubble, queste velocità s o n o supposte proporzionali alla distanza da G.) Il teorema di Birkhoff afferma che, per calcolare il m o t o di una galassia A relativamente a G, è sufficiente tener conto della massa contenuta all’interno della sfera, con centro in G, la cui superficie, indicata qui dalla linea tratteggiata, passa per A. Se A n o n è t r o p p o lontana da G, il c a m p o gravitazionale della m a t e r i a contenuta all’interno della sfera sarà tale da consentire il calcolo del m o t o di A mediante la semplice applicazione delle formule della meccanica newtoniana.

densità cosmica, ogni galassia che si muova secondo la legge di Hubble o supererà la velocità di fuga ed evaderà nell’infinito o avrà una velocità inferiore alla velocità di fuga e quindi in futuro ricadrà a un dato momento verso di noi. La densità critica è, semplicemente, il valore della densità cosmica in corrispondenza del quale la velocità di fuga di ciascuna galassia

Figura 4. Espansione e contrazione dell’universo. La distanza fra galassie tipiche è rappresentata qui (in unità arbitrarie) in funzione del tempo, per due possibili modelli cosmologici. Nel caso di un « universo aperto », l’universo è infinito; la densità è minore della velocità critica; e l’espansione, pur rallentando, continuerà per sempre. Nel caso di un « universo chiuso », l’universo è finito; la densità è maggiore della densità critica; e l’espansione finirà con l’arrestarsi e l’essere seguita da una contrazione. Queste curve sono calcolate usando equazioni di campo di Einstein senza ricorrere a una costante cosmologica, per un universo dominato dalla materia.

e g u a g l i a l a v e l o c i t à indicata dalla l e g g e d i H u b b l e . L a d e n s i t à critica p u ò d i p e n d e r e s o l o d a l l a c o s t a n t e d i H u b b l e e , d i f a t t o , risulta e s s e r e i n u n r a p p o r t o d i p r o p o r z i o n a l i t à s e m p l i c e c o l q u a d r a t o d e l l a c o s t a n t e d i H u b b l e . (Si v e d a l a n o t a m a t e m a t i -

c a 2 , p p . 1 7 5 s g . )

L a p r e c i s a d i p e n d e n z a dal t e m p o d e l l e d i m e n s i o n i d e l l ‘ u n i -

v e r s o ( o s s i a d e l l a d i s t a n z a fra d u e qualsiasi g a l a s s i e t i p i c h e ) p u ò e s s e r e d e t e r m i n a t a r i c o r r e n d o a r a g i o n a m e n t i simili, ma i risultati s o n o p i u t t o s t o c o m p l e s s i (cfr. f i g . 4 ) . C’è p e r ò u n ri-s u l t a t o s e m p l i c e c h e sarà per n o i m o l t o i m p o r t a n t e p i ù a v a n t i .

N e l p e r i o d o i n i z i a l e l e d i m e n s i o n i d e l l ‘ u n i v e r s o v a r i a v a n o i n r a g i o n e d i u n a p o t e n z a s e m p l i c e del t e m p o : l a p o t e n z a d i d u e terzi se la d e n s i t à di r a d i a z i o n e era trascurabile, la p o t e n z a di u n m e z z o s e l a d e n s i t à d i r a d i a z i o n e s u p e r a v a q u e l l a d e l l a m a -

teria. (Si v e d a i n p r o p o s i t o l a n o t a m a t e m a t i c a 3 , p p . 1 7 7 s g g . ) L ‘ u n i c o a s p e t t o dei m o d e l l i c o s m o l o g i c i d i F r i e d m a n n c h e n o n p o s s a e s s e r e i n t e s o s e n z a l’ausilio d e l l a relatività g e n e r a l e è il

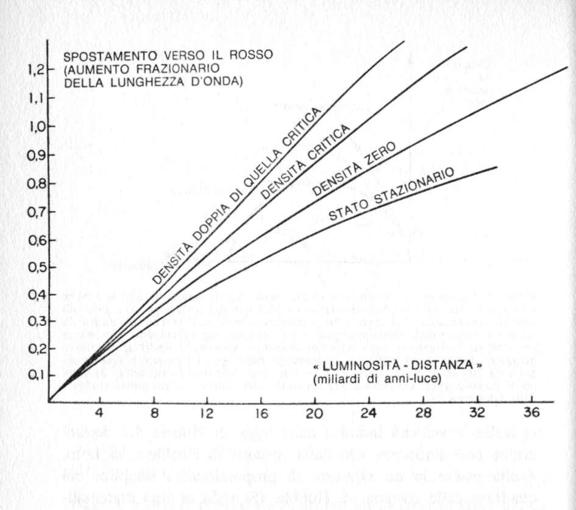
Figura 5. Spostamento verso il rosso e distanza. Lo spostamento verso il rosso è presentato come una funzione della distanza, per quattro possibili teorie cosmologiche. (Per la precisione, la « distanza » è qui una « distanza di luminosità », ossia una distanza inferita, per un oggetto di luminosità intrinseca o assoluta supposta come nota, da osservazioni della sua luminosità apparente.) Le curve recanti le indicazioni « densità doppia di quella critica», « densità critica » e « densità zero » sono calcolate nel modello di Friedmann, usando le equazioni di campo di Einstein per un universo dominato dalla materia senza far ricorso alla costante cosmologica; esse corrispondono rispettivamente a un universo chiuso, appena aperto e aperto. (Si veda la figura 4.) La curva recante l’indicazione « stato stazionario » corrisponde a ogni teoria in cui l’aspetto dell’universo non muti col tempo. Le osservazioni attuali non sono del tutto in armonia con la curva dello « stato stazionario», ma non sono tali da consentire di propendere con decisione per una delle altre possibilità, perché nelle teorie non stazionarie l’evoluzione galattica rende molto problematica la determinazione delle distanze. Tutte le curve sono state tracciate assegnando alla costante di Hubble il valore oggi accettato di 15 chilometri al secondo per ogni milione di anni-luce di distanza (corrispondente a un tempo di espansione caratteristico di 20 miliardi di anni), ma possono essere usate per ogni altro valore della costante di Hubble semplicemente attribuendo un’altra scala a tutte le distanze.

L’espansione dell’universo 51

rapporto fra densità e geometria: l’universo è aperto e infinito o chiuso e finito a seconda che la velocità delle galassie sia maggiore o minore della velocità di fuga.

Un modo per stabilire se le velocità galattiche superino o no la velocità di fuga consiste nel misurare il ritmo del loro rallentamento. Se la loro decelerazione è minore (o maggiore) di una certa soglia, la velocità di fuga viene (o non viene) superata. In pratica ciò significa che si deve esaminare l’anda-mento della curva dello spostamento verso il rosso in funzione della distanza per galassie molto lontane (cfr. fig. 5). Procedendo da un universo finito, più denso, a un universo infinito, meno denso, la curva dello spostamento verso il rosso in funzione della distanza si appiattisce per distanze molto grandi.

Lo studio della forma della curva spostamento verso il rosso-distanza a distanze molto grandi è spesso designato come

« programma di Hubble ».

Alla realizzazione di questo programma sono stati dedicati sforzi enormi da parte di Hubble, Sandage, e recentemente da parte anche di altri studiosi. Finora i risultati sono stati del tutto inconcludenti. Il guaio è che nella stima delle distanze di galassie lontane è impossibile utilizzare come indicatori di distanza variabili cefeidi o stelle molto brillanti; dobbiamo piuttosto stimare la distanza sulla base della luminosità apparente delle galassie stesse. Ma come possiamo verificare che le galassie che studiamo abbiano tutte la medesima luminosità asso-

luta? (Si ricordi che la luminosità apparente è l’energia di radiazione da noi ricevuta per unità di superficie al telescopio, mentre la luminosità assoluta è l’energia di radiazione totale emessa in tutte le direzioni dall’oggetto astronomico; la luminosità apparente è proporzionale alla luminosità assoluta e inversamente proporzionale al quadrato della distanza.) Ci sono gravi rischi connessi a effetti di selezione: quanto più lontano spingiamo lo sguardo, tanto più tendiamo a utilizzare galassie di luminosità assoluta sempre maggiore. Un problema an-52 I primi tre minuti

cor più complesso è legato all’evoluzione delle galassie. Quando osserviamo galassie molto remote le vediamo com’erano miliardi di anni fa, quando la luce iniziò il suo lunghissimo viaggio verso di noi. Se le galassie tipiche erano allora più brillanti di quanto non siano oggi, ne sottovaluteremmo inevitabilmente la distanza. Una possibilità, prospettata ultimamen-te da J.P. Ostriker e S.D. Tremaine, di Princeton, è che le galassie maggiori si evolvano in conseguenza non soltanto della evoluzione delle loro singole stelle, ma anche della cattura di piccole galassie vicine. Passerà molto tempo prima che possiamo essere certi di avere una sufficiente conoscenza quantitativa di questi vari tipi di evoluzione galattica.

Secondo la migliore inferenza che possa essere tratta oggi dal programma di Hubble, la decelerazione di galassie remote sembra piuttosto scarsa. Ciò significherebbe che esse stanno muovendosi a una velocità superiore alla velocità di fuga: l’universo sarebbe aperto e destinato a espandersi eternamente.

Questa conclusione è avallata da stime della densità cosmica; la materia visibile nelle galassie sembra ammontare a non più di una piccola percentuale della densità critica. Anche su questo problema sussistono però delle incertezze. Le stime della massa delle galassie sono venute crescendo in anni recenti.

Inoltre, com’è stato suggerito da George Field, di Harvard, e da altri, potrebbe esserci un gas intergalattico di idrogeno ionizzato, capace di fornire una densità cosmica critica di materia pur essendo finora sfuggito all’osservazione.

Fortunatamente non è necessario pervenire a una soluzione precisa nel campo della geometria su vasta scala dell’universo per trarre conclusioni sul suo inizio. L’universo, infatti, ha una sorta di orizzonte, che si contrae rapidamente quando volgiamo lo sguardo indietro, verso il principio.

Nessun segnale può viaggiare a una velocità superiore a quella della luce, per cui in ogni momento noi si possa isti-tuire un rapporto fisico, fosse pure solo quello dell’osservaL’espansione dell’universo 53

zione, unicamente con eventi che si siano verificati in una zona abbastanza vicina a noi perché un raggio di luce abbia avuto il tempo di raggiungerci a partire dall’inizio dell’universo. Ogni evento che abbia avuto luogo oltre tale distanza non potrebbe avere ancora alcun effetto su di noi: si trova oltre l’orizzonte.

Se l’universo ha oggi un’età di 10 miliardi di anni, l’orizzonte si trova a una distanza di 30 miliardi di anni-luce. Quando l’universo aveva invece un’età di soli pochi minuti, l’orizzonte si trovava a una distanza di pochi minuti-luce: meno dell’attuale distanza fra la Terra e il Sole. È vero anche che l’intero universo era allora più piccolo, nel senso che il distacco fra due corpi scelti a piacere era allora minore di quanto non sia oggi.

Se però volgiamo lo sguardo indietro verso il principio dell’universo, vediamo che la distanza rispetto all’orizzonte diminuisce più rapidamente delle dimensioni dell’universo. Le dimensioni dell’universo sono proporzionali alla potenza di un mezzo o due terzi del tempo (cfr. nota matematica 3, pp. 177 sgg.), mentre la distanza dall’orizzonte è in proporzione semplice col tempo, in modo tale che, per tempi sempre più vicini al principio, l’orizzonte cinge una parte sempre più piccola dell’universo (cfr. fig. 6).

In conseguenza di questo restringersi di orizzonti nei primi minuti di vita dell’universo, la curvatura dell’universo nel suo insieme risulta sempre meno differenziata man mano che il nostro occhio si addentra in tempi sempre più remoti. Pur non avendo ancora rivelato l’estensione o il futuro dell’universo, l’attuale teoria cosmologica e l’attuale osservazione astronomica ci danno dunque un’immagine abbastanza chiara del suo passato.

Le osservazioni che abbiamo discusso in questo capitolo ci hanno dischiuso una visione dell’universo che è grandiosa nella sua semplicità. L’universo si sta espandendo in modo uniforme e isotropo: lo stesso modello di espansione si presenta a osservatori che si trovino in tutte le galassie tipiche, e in tutte

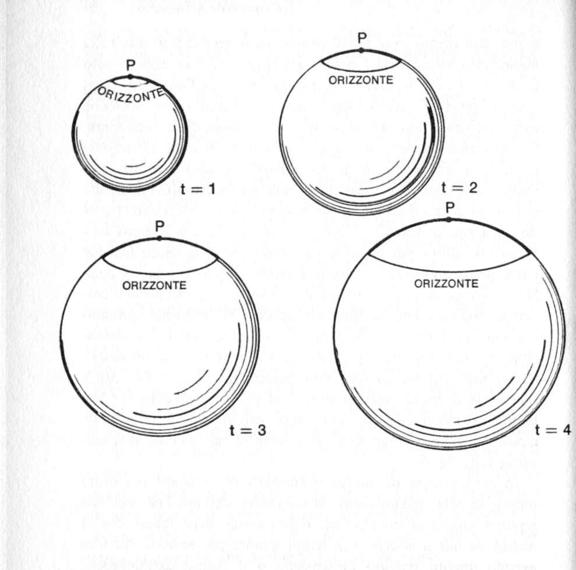
Figura 6. Gli orizzonti in un universo in espansione. L’universo è rappresentato simbolicamente come una sfera, in quattro momenti separati da intervalli di tempo uguali. L’« orizzonte » di un punto dato P è la distanza da oltre la quale i segnali di luce non hanno ancora avuto il tempo di raggiungere P. La parte dell’universo che si trova all’interno dell’orizzonte è indicata qui dalla calotta della sfera non ombreggiata. La distanza di P dall’orizzonte cresce in proporzione diretta al tempo. 11 « raggio » dell’universo cresce invece come la radice quadrata del tempo, conformemente al caso di un universo dominato dalla radiazione. Di conseguenza, man mano che procediamo a ritroso nel tempo avvici-nandoci sempre più agli inizi dell’universo, l’orizzonte cinge una porzione dell’universo sempre più piccola.

L’espansione dell’universo 55

le direzioni. Man mano che l’universo si espande, le lunghezze d’onda dei raggi luminosi si dilatane in proporzione alla distanza fra le galassie. L’espansione non è dovuta, secondo una opinione accettata pressoché universalmente, a una sorta di repulsione cosmica, bensì è solo l’effetto delle velocità residue derivanti da un’esplosione verificatasi in passato. Queste velocità vanno rallentando gradualmente sotto l’influsso della gravitazione; questa accelerazione negativa ci appare alquanto lenta, suggerendoci che la densità dell’universo sia bassa e il suo campo gravitazionale troppo debole sia per rendere l’universo spazialmente finito sia per invertire infine il processo di espansione e dare l’avvio a una contrazione. I nostri calcoli ci consentono di estrapolare l’espansione dell’universo retrocedendo nel tempo e ci rivelano che l’espansione deve avere avuto inizio fra i 10 e i 20 miliardi di anni or sono.