LA SEGUNDA LEY EN ACCIÓN

Supongamos, ahora, que partimos de un sistema en una situación muy especial, como sucedía cuando todo el gas estaba en un rincón de la caja. En los instantes siguientes el gas se expandirá y ocupará rápidamente volúmenes cada vez mayores. Tras cierto tiempo, se establecerá el equilibrio térmico. ¿Cuál es nuestra imagen de este proceso en términos del espacio de fases?

En cada paso, el estado detallado de posiciones y movimientos de las partículas vendrá descrito por un simple punto en el espacio de fases. A medida que el gas evoluciona, este punto se mueve por el espacio de fases y sus recorridos precisan toda la historia de las partículas del gas. El punto parte de una región pequeñísima, la región que representa la colección de posibles estados iniciales, para los cuales todo el gas está en una esquina particular de la caja.

A medida que el gas comienza a expandirse, nuestro punto en movimiento entrará en un volumen mayor del espacio de fases, que corresponde a los estados en los que el gas se ha expandido por la caja. El punto en el espacio de fases sigue invadiendo volúmenes mayores a medida que el gas se extiende, de manera que cada nuevo volumen empequeñece totalmente a aquellos en los que el punto había estado antes ¡por factores absolutamente extraordinarios! (véase figura VII.5).

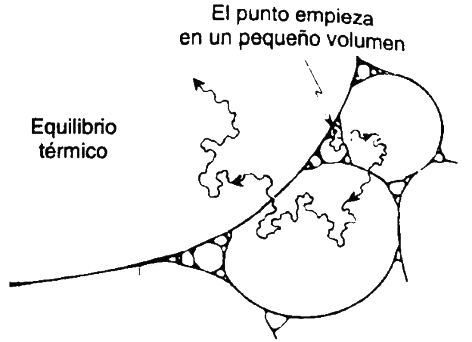
FIGURA VII.5. La segunda ley de la termodinámica en acción: conforme avanza el tiempo, el punto en el espacio de fases invade gradualmente compartimientos de cada vez mayor volumen. Como resultado la entropía se incrementa continuamente.

En cada caso, una vez que el punto haya entrado en el volumen mayor, no existirá posibilidad de que halle los volúmenes anteriores más pequeños. Finalmente, se perderá en el volumen más grande de todos: el correspondiente al equilibrio térmico. Este volumen ocupa prácticamente la totalidad del espacio de fases.

Podemos asegurar virtualmente que, en su deambular aleatorio, nuestro punto en el espacio de fases no encontrará pronto ninguno de los volúmenes pequeños. Una vez que se haya alcanzado el estado de equilibrio térmico, el estado permanecerá allí, efectivamente, para siempre. Vemos así que la entropía del sistema, al proporcionar una medida logarítmica del volumen del compartimento apropiado del espacio de fases, tenderá inexorablemente a aumentar.^[7.5]

¿Estamos ante una explicación de la segunda ley? En efecto, podemos suponer que nuestro punto en el espacio de fases no se mueve de ninguna manera especialmente concebida, y si parte de un volumen pequeñísimo en el espacio de fases, correspondiente a una entropía pequeña, entonces a medida que el tiempo avanza será extraordinariamente probable que entre en volúmenes del espacio de fases sucesivamente mayores (los cuales corresponderán a valores gradualmente crecientes de la entropía).

Pero hay algo extraño en lo que se sigue a partir de este argumento: parece que hemos deducido una conclusión con asimetría temporal. La entropía crece en la dirección positiva del tiempo, y por ello debería disminuir en la dirección inversa. ¿De dónde procede tal asimetría temporal? No hemos introducido ninguna ley física con asimetría temporal. La asimetría temporal procede simplemente del hecho de que el sistema ha partido de un estado muy especial (esto es, de baja entropía), y al haber empezado así lo hemos visto evolucionar en la dirección del futuro y hemos encontrado que la entropía crece. Este incremento de la entropía va de acuerdo con el comportamiento de los sistemas en nuestro universo, pero podríamos perfectamente haber aplicado este mismo argumento en la dirección inversa del tiempo. Especificaremos de nuevo que en un instante dado el sistema se halla en un estado de baja entropía. ¿Cuál es la secuencia más probable de estados que lo preceden?

Ensayemos el argumento en forma inversa. Consideremos, como antes, que el estado de baja entropía es el de todo el gas en una esquina de la caja. Nuestro punto en el espacio de fases está ahora en la misma región minúscula de la que partimos antes, pero sigamos su historia hacia atrás. Si imaginamos que el punto en el espacio de fases deambula de una forma aleatoria, como antes, entonces esperamos que, a medida que seguimos este movimiento hacia atrás en el tiempo, alcanzará pronto el volumen considerablemente mayor del espacio de fases que alcanzó antes, correspondiente al gas extendido un poco por la caja, pero no en equilibrio térmico. Y seguirá alcanzando volúmenes cada vez mayores, a tal grado que cada nuevo volumen empequeñecerá a los previos. Y así, si retrocedemos todavía más en el tiempo, lo encontraremos en el volumen más grande de todos: el equilibrio térmico.

Ahora hemos deducido que en cierto instante todo el gas estaba concentrado en la esquina de la caja. Partió del equilibrio térmico, luego comenzó a concentrarse en un extremo de la caja, más y más, hasta que se agrupó en el pequeño volumen especificado de la esquina. La entropía tendría que haber estado decreciendo todo el tiempo: ¡partió del valor alto de equilibrio y luego decreció gradualmente hasta que alcanzó el valor muy bajo correspondiente al gas concentrado en la pequeña esquina de la caja!

¡Por supuesto, esto no se parece en nada a lo que realmente sucede en nuestro universo! La entropía no sólo no disminuye, sino que aumenta. Si supiéramos que todo el gas estaba concentrado en un rincón de la caja en un instante particular, entonces una situación mucho más probable que hubiera precedido a aquélla habría sido la de que el gas se hubiera mantenido en el rincón mediante una partición, que hubiese sido rápidamente eliminada. O quizá el gas estuvo en un estado congelado o líquido y fue calentado rápidamente para volverse gaseoso. Para cualquiera de estas posibles opciones, la entropía era aún menor en los estados previos. La segunda ley realmente se satisfacía y la entropía estaba creciendo, dicho de otra forma, en la dirección inversa del tiempo, realmente disminuía.

¡Ahora tenemos que nuestro argumento nos ha dado una respuesta totalmente equivocada! Nos ha dicho que la forma más probable de tener el gas en la esquina de la caja sería partir del equilibrio térmico y que, con la entropía reduciéndose continuamente, el gas se agruparía en la esquina. Mientras que, de hecho, es extraordinariamente improbable que suceda así en nuestro mundo real. En éste, el gas partiría de un estado aún menos probable (esto es, de menor entropía), y la entropía aumentaría continuamente hasta alcanzar el valor que tendrá posteriormente cuando el gas esté concentrado en la esquina.

Nuestro argumento parece ser bueno cuando se aplica en la dirección del futuro, pero no en la dirección del pasado. Para el futuro prevemos correctamente que, de donde quiera que parta el gas en la esquina, lo más probable es que llegue a alcanzar el equilibrio térmico, y no que aparezca una partición o que el gas se congele o se haga líquido. Semejantes posibilidades representarían el tipo de comportamiento con disminución de entropía en la dirección del futuro que ya hemos descartado. En la dirección del pasado, en cambio, semejantes opciones «anómalas» son las que sucederían —y no serían en absoluto anómalas. ¡Nuestro argumento del espacio de fases nos dio una respuesta totalmente errónea cuando tratamos de aplicarla en la duración inversa del tiempo!

Evidentemente, todo lo anterior arroja algunas dudas sobre el argumento original. No hemos deducido la segunda ley. Lo que realmente mostraba el argumento era que para un estado de baja entropía dado (digamos para un gas concentrado en una esquina de una caja), entonces, en ausencia de otros factores que impongan restricciones al sistema, se espera que la entropía aumente en ambas direcciones en el tiempo a partir del estado dado (véase figura VII.6).

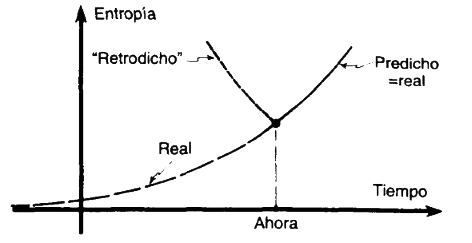
FIGURA VII.6. Si aplicamos el argumento representado en la figura VII.5 pero con una dirección inversa del tiempo, «retrodecimos»^[7.6] que la entropía debe también incrementarse en el pasado, a partir de su valor presente. Esto está en abierta contradicción con la observación.

Y si tal argumento no ha funcionado en la dirección del pasado, es precisamente porque existían tales factores: había algo en el pasado que limitaba al sistema, algo que obligaba a la entropía a ser baja. La tendencia hacia una entropía alta en el futuro no es sorpresa. Los estados de alta entropía son, en cierto sentido, los estados «naturales» que no necesitan más explicación, pero los estados de baja entropía en el pasado son un enigma. ¿Qué obligaba a la entropía de nuestro mundo a ser tan baja en el pasado? La presencia común de estados para los que la entropía es absurdamente baja, es un hecho sorprendente del universo real en el que habitamos —aunque tales estados son tan comunes y familiares para nosotros que no tendemos a sorprendernos con ellos—. ¡Nosotros mismos somos configuraciones de entropía ínfima! No deberíamos entonces alarmarnos si, dado un estado de baja entropía, la entropía después resulta ser mayor. ¡Lo que debería sorprendernos es que la entropía se haga más pequeña a medida que nos adentramos en el pasado!