NÚMEROS REALES

Recordemos que los números naturales son las cantidades enteras:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …

Son los más elementales y básicos entre los diferentes tipos de números. Cualquier entidad discreta puede cuantificarse mediante el uso de números naturales: podemos hablar de veintisiete ovejas en un prado, de dos relámpagos, doce noches, mil palabras, cuatro conversaciones, cero ideas nuevas, un error, seis ausentes, dos cambios de dirección, etc. Los números naturales pueden sumarse o multiplicarse para dar nuevos números naturales. Son los objetos de nuestra discusión general de los algoritmos, como la que se dio en el capítulo precedente. Sin embargo, algunas operaciones importantes pueden llevarnos fuera del dominio de los números naturales; la resta es la más sencilla de éstas. Para definir la resta de una forma sistemática necesitamos los números negativos; podemos establecer, para este propósito, el sistema global de los enteros

…, −6, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, 6, 7, …

Ciertas cosas, como la carga eléctrica, los balances bancarios o las fechas^[3.2] se cuantifican mediante números de este tipo. Pese a todo, estos números son aún de alcance demasiado limitado puesto que nos quedaríamos bloqueados cuando tratáramos de dividir un número por otro. En consecuencia, necesitaremos las fracciones o números racionales como son llamados

0, 1, −1, 1/2, −1/2, 2,−2, 3/2, −3/2, 1/3, …

Esto es suficiente para las operaciones de la aritmética finita, pero para muchos otros propósitos necesitamos ir más allá e incluir operaciones infinitas o de paso al límite. Por ejemplo, la familiar —y de gran importancia en matemáticas— cantidad π aparece en muchas de estas expresiones infinitas. En particular, tenemos

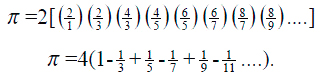
Estas son expresiones famosas, habiendo sido encontrada la primera por el matemático, gramático y experto criptógrafo inglés John Wallis en 1665; y la segunda por el matemático y astrónomo escocés (e inventor del primer telescopio reflector) James Gregory en 1671. Como sucede con π, los números definidos de esta forma no deben ser racionales (esto es, no de la forma n/m, en donde n y m son enteros con m distinto de cero). El sistema de números necesita ser ampliado para poder incluir tales cantidades.

Este sistema ampliado de números se denomina sistema de los números «reales», aquellos números familiares que pueden representarse como expansiones decimales infinitas, tales como:

−583,70264439121009538…

En términos de una representación semejante tenemos la bien conocida expresión para n:

π = 3,14159265358979323846…

Entre los tipos de números que también pueden representarse de este modo están las raíces cuadradas (o las raíces cúbicas o las raíces cuartas, etc.) de números racionales positivos, tales como:

√2 =1,414221356237309504…

o, de hecho, la raíz cuadrada (o raíz cúbica, etc.) de cualquier número real positivo, como sucede con la expresión para π encontrada por el gran matemático suizo Leonhard Euler:

π = √[6 (1 + 1/4 + 1/9 + 1/25 + 1/36 + …)]

Los números reales son, en efecto, el tipo familiar de números con los que tenemos que trabajar en la vida de cada día, aunque normalmente estamos interesados sólo en aproximaciones a tales números y preferimos trabajar con expansiones que incluyen sólo algunas cifras decimales. Sin embargo, en las proposiciones matemáticas los números reales tienen que ser especificados exactamente, y necesitamos algún tipo de descripción infinita como pueda ser una completa expansión decimal infinita, o quizá alguna otra expresión matemática infinita como las fórmulas anteriores para n dadas por Wallis, Gregory o Euler. (Normalmente utilizaré expansiones decimales en mis descripciones, pero sólo porque resultan más familiares. Para un matemático hay varias maneras bastante más satisfactorias de presentar los números reales pero no necesitamos preocuparnos por eso ahora).

Podría dar la impresión de que es imposible considerar una expansión infinita completa pero no es así. Un ejemplo sencillo en el que podemos considerar claramente la secuencia completa es

1/3 = 0,3333333333333333…,

donde los puntos nos indican que la serie de los 3's continúa indefinidamente. Para considerar esta expansión, todo lo que necesitamos saber es que la expansión continúa de la misma forma indefinidamente con 3's. Todo número racional tiene una expansión decimal repetida (o finita), tal como

93/74 = 1,2567567567567567567…,

donde la secuencia 567 se repite indefinidamente, y ésta también puede ser considerada en su totalidad. También, la expresión

0,220002222000002222220000000222222220…,

que define un número irracional, puede ser considerada en su totalidad (las cadenas de 0's y 2's incrementan su longitud en uno cada vez) y pueden darse muchos ejemplos similares.

En cada caso nos damos por satisfechos cuando conocemos una regla con arreglo a la que se construye la expansión. Si hay algún algoritmo que genera los sucesivos dígitos, el conocimiento de dicho algoritmo nos proporciona una forma de considerar toda la expansión decimal infinita. Los números reales cuya expansión puede ser generada mediante algoritmos se llaman números computables . (El uso de una expansión decimal en lugar de, pongamos por caso, una binaria no tiene importancia aquí. Los números que son «computables» en este sentido son los mismos cualquiera que sea la base utilizada para la expansión). Los números reales π y √2 que hemos estado considerando son ejemplos de números computables. En ambos casos sería un poco complicado establecer la regla en detalle, pero no hay dificultad de principio.

Sin embargo, existen también muchos números reales que no son computables en este sentido. Hemos visto en el último capítulo que existen secuencias no computables que están, a pesar de todo, perfectamente bien definidas. Por ejemplo, podríamos tomar la expansión decimal cuyo n-ésimo dígito es 1 o 0 según se detenga o no la n-ésima máquina de Turing actuando sobre el número n. En general sólo pedimos que para un número real haya cierta expansión decimal infinita. No pedimos que exista un algoritmo para generar el n-ésimo dígito, ni siquiera que conozcamos algún tipo de regla que en principio defina cuál es realmente el n-ésimo dígito.^[3.3] El trabajo con los números computables es cosa muy difícil. No se puede hacer que todas las operaciones sean computables aun cuando se trabaje sólo con números computables. Por ejemplo, ¡ni siquiera es un asunto computable el decidir, en general, si dos números computables son iguales o no! Por razones de este tipo, es preferible trabajar, en su lugar, con todos los números reales, para los que las expansiones decimales pueden ser cualesquiera y no necesitan ser, pongamos por caso, una secuencia computable.

Señalaré finalmente que existe una identificación entre un número real cuya expansión decimal termina con una sucesión infinita de 9s y otro cuya expansión termina con una sucesión infinita de 0s; por ejemplo

−27.1860999999… = −27.1861000000…