EL SPIN Y LA ESFERA DE ESTADOS DE RIEMANN

El spin se considera a veces como «la más» cuántica de todas las cantidades físicas, y es prudente que le prestemos atención. ¿Qué es el spin? En esencia, es una medida de la rotación de una partícula. El término «spin» sugiere algo como el giro de una bola de cricket o de béisbol. Recordemos el concepto de momento angular que, como la energía y el momento, es una magnitud que se conserva (véase capítulo V). El momento angular de un cuerpo persiste mientras el cuerpo no sea perturbado por fuerzas de rozamiento o de otro tipo. En esto consiste, en realidad, el spin cuántico. Pero ahora lo que nos interesa es el giro de una sola partícula, no el movimiento orbital de miríadas de partículas individuales en torno a su centro de masas común (que sería el caso de una bola de cricket). Un hecho físico notable es que la mayoría de las partículas encontradas en la naturaleza realmente gira en este sentido, con una cantidad específica para cada tipo de partícula.^[6.14] No obstante, el spin de una simple partícula cuántica tiene propiedades peculiares que no son ni mucho menos las que esperaríamos a partir de nuestras experiencias con giros de bolas de cricket o cosas similares.

En primer lugar, la magnitud del spin de una partícula es siempre la misma para ese tipo concreto de partícula. Solamente la dirección del eje de giro es la que puede llegar a variar (de una muy extraña forma que ya abordaremos). ¡Esto está en absoluto contraste con una bola de cricket, que puede girar en cualquier dirección y a diferentes velocidades, de acuerdo con la manera como sea lanzada! Para un electrón, protón o neutrón la cantidad de spin es siempre ℏ/2, o sea únicamente la mitad del menor valor positivo que admitía originalmente Bohr para sus momentos angulares cuantizados de los átomos. (Recordemos que estos valores eran 0, ℏ , 2ℏ , 3ℏ , …). Aquí requerimos la mitad de la unidad básica ℏ, y, en cierto sentido, ℏ/2 es ella misma la unidad básica fundamental. Esta cantidad de momento angular no estaría permitida para un objeto compuesto de un cierto número de partículas orbitando sin que ninguna de ellas estuviese girando sobre sí misma. Sólo aparece porque el spin es una propiedad intrínseca de la propia partícula (es decir, que no surge del movimiento orbital de sus «partes» en torno a su centro).

Una partícula cuyo spin es un múltiplo impar de ℏ/2 (es decir, ℏ/2, 3ℏ/2, o 5ℏ/2, etc.) se llama fermión, y exhibe una curiosa rareza de la descripción cuántica: ¡una rotación completa de 360° transforma su vector de estado no en sí mismo sino en menos sí mismo! La mayoría de las partículas de la naturaleza son realmente fermiones, y más adelante oiremos más sobre ellas y sus singulares maneras de existir —tan vitales para nosotros—. Las partículas restantes, para las que el spin es un múltiplo par de ℏ/2, es decir, un múltiplo entero de ℏ (a saber 0, ℏ, ℏ, 3ℏ, …), se llaman bosones. Tras una rotación de 360° el vector de estado de un bosón vuelve a sí mismo, no a su negativo.

Consideremos una partícula de spin 1/2, esto es con un valor ℏ/2 para el spin. Para ser más concreto me referiré a la partícula como un electrón, pero un protón o un neutrón, o incluso un tipo adecuado de átomo, servirían igual. (Se admite que una «partícula» puede poseer partes individuales con tal de que pueda ser tratada cuánticamente como un todo simple, con un momento angular total bien definido).

Tomemos el electrón en reposo y consideremos sólo su estado de spin. El espacio de estados cuánticos (espacio de Hilbert) resulta ser ahora bidimensional, de modo que podemos tomar una base de sólo dos estados. Representaré estos estados como |↑〉 y |↓〉, con el propósito de indicar que para |↑〉 el spin gira hacia la derecha, alrededor de la dirección vertical hacia arriba, mientras que para |↓〉, gira hacia la derecha también, pero alrededor de la dirección hacia abajo (figura VI.24). Los estados |↑〉 y |↓〉 son mutuamente ortogonales y, suponemos, normalizados (|↑|² = |↓|² = 1). Cualquier posible estado de spin del electrón es una superposición lineal, digamos w|↑〉 + z|↓〉 , de sólo los dos estados ortonormales |↑〉 y |↓〉, es decir de arriba y abajo.

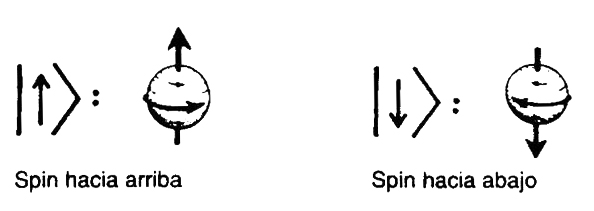
FIGURA VI.24. Una base para los estados de spin de un electrón consta de sólo dos estados. Éstos pueden tomarse como spin hacia arriba y spin hacia abajo.

Ahora bien, no hay nada especial en las direcciones «arriba» y «abajo». Exactamente igual podríamos haber descrito el spin girando en cualquier otra dirección (es decir, hacia la derecha o hacia la izquierda) cualquier otra dirección, pongamos por caso derecha |→〉 como opuesto a izquierda |←〉. Entonces (para una elección adecuada de la escala compleja para |↑〉 y |↓〉), encontramos^[6.15]

|→〉 = |↑〉 + |↓〉 y |←〉 = |↑〉 − |↓〉

Lo que nos da una nueva visión: cualquier estado de spin electrónico es una superposición lineal de los dos estados ortogonales |→〉 y |←〉, es decir, de derecha e izquierda. Podríamos escoger, en su lugar, alguna dirección completamente arbitraria, por ejemplo la dada por el vector de estado |↗〉. Esta es, nuevamente, una cierta combinación lineal compleja de |↑〉 y |↓〉. Digamos que

|↗〉 = w|↑〉 + z|↓〉

y todo estado de spin será una superposición lineal de ese estado y el estado ortogonal |↙〉, que apunta en dirección opuesta^[6.16] a |↗〉. (Nótese que el concepto de «ortogonal» en el espacio de Hilbert no corresponde necesariamente a la formación de «ángulos rectos» en el espacio ordinario. En estos casos, los vectores ortogonales del espacio de Hilbert corresponden más a direcciones diametralmente opuestas en el espacio, que a direcciones que forman ángulos rectos).

¿Cuál es la relación geométrica entre la dirección que determina |↗〉 en el espacio y los dos números complejos w y z? Puesto que el estado físico dado por |↗〉 queda inalterado si multiplicamos |↗〉 por un número complejo distinto de cero, únicamente la razón de z a w será la realmente significativa. Escribamos

q = z/w

para este cociente. Aquí q corresponderá simplemente a algún número complejo, excepto porque el valor «q = ∞» también está permitido cuando hay que cubrir la situación w = 0, es decir, cuando la dirección del spin es la vertical hacia abajo. A menos que q = ∞, podemos representar q como un punto en el plano de Argand, igual que hicimos en el capítulo III.

Imaginemos que este plano de Argand está situado horizontalmente en el espacio, con el eje real en la dirección hacia la «derecha» en la descripción anterior (esto es, en la dirección del estado de spin |→〉). Imaginemos una esfera de radio unidad cuyo centro está en el origen de este plano de Argand, de modo que los puntos 1, i, −1, −i están todos en el ecuador de la esfera. Consideremos el punto en el Polo Sur, que designaremos ∞. Proyectemos entonces desde este punto, de modo que el plano de Argand entero se aplique sobre la esfera. Así, cualquier punto q en el plano de Argand corresponderá a un punto q único en la esfera, obtenido al alinear los dos puntos con el Polo Sur (figura VI.25). Esta correspondencia se llama proyección estereográfica y tiene muchas propiedades geométricas hermosas (por ejemplo, conserva los ángulos y aplica círculos en círculos).

FIGURA VI.25. La esfera de Riemann, representada aquí como el espacio de estados físicamente distintos de una partícula de spin 1/2. La esfera se proyecta estereográficamente desde su Polo Sur (∞) en el plano de Argand que pasa por su ecuador.

La proyección nos da una caracterización de los puntos de la esfera con base en números complejos junto con ∞, mediante el conjunto de razones complejas q posibles. Una esfera caracterizada de esta forma particular se llama esfera de Riemann. Su importancia —para los estados de spin del electrón— reside en que la dirección del spin definido por |↗〉 = w|↑〉 + z|↓〉 viene dada por la dirección real desde el centro al punto q = z/w marcado en la esfera de Riemann. Notemos que el Polo Norte corresponde al estado |↑〉, que está dado por z = 0, es decir por q = 0, y el Polo Sur a |↓〉, dado por w = 0, es decir por q = ∞. El punto más extremo hacia la derecha está caracterizado por q = 1, que proporciona el estado |→〉 = |↑〉 + |↓〉, y el punto más extremo a la izquierda por q = −1, que proporciona el estado |←〉 = |↑〉 − |↓〉.

El punto más alejado hacia el fondo de la esfera esta caracterizado por q = i, correspondiente al estado |↑〉 + i|↓〉, en el que el spin apunta alejándose de nosotros, y el punto más próximo, q = −i, corresponde a |↑〉 − i|↓〉, en el que el spin apunta directamente hacia nosotros. El punto más general, caracterizado por q, corresponde a |↑〉 + q|↓〉.

¿Cómo enlaza todo esto con las mediciones que pudiéramos realizar sobre el spin del electrón?^[6.17] Seleccionemos alguna dirección en el espacio; y llamémosla dirección α. Si medimos el spin del electrón en esta dirección, la respuesta «sí» indica que el electrón está girando hacia la derecha, alrededor de α, mientras que «no» dice que gira en la dirección opuesta.

Ahora supongamos que la respuesta es «sí»; y caractericemos el estado resultante así: |α〉. Si repetimos la medición utilizando exactamente la misma dirección a que antes, entonces encontraremos que la respuesta es de nuevo «sí» (con 100% de probabilidad). Pero si para la segunda medición cambiamos la dirección a una nueva dirección β, entonces vamos a encontrar que hay una probabilidad más pequeña para la respuesta «sí», y que el estado salta ahora a |β〉. Por lo que existiría alguna posibilidad de que la respuesta a la segunda medición fuera «no», y que el estado saltara a la dirección opuesta a β. ¿Cómo calcular esa probabilidad? La respuesta está contenida en la receta dada al final de la sección previa. La probabilidad de «sí» resulta ser, para la segunda medición,

1/2(1 + cos θ),

donde θ es el ángulo entre las direcciones^[6.18] de α y β.

Y la probabilidad de «no» para la segunda medición es, en consecuencia,

1/2(1 − cos θ),

Como podemos ver, si la segunda medición se realiza en ángulo recto con la primera, la probabilidad de cualquiera de los resultados es del 50% (cos 90° = 0): entonces ¡el resultado de la segunda medición será completamente aleatorio! Si el ángulo entre las dos mediciones es agudo, entonces la respuesta «sí» es más probable que «no». Si es obtuso, entonces «no» es más probable que «sí». En el caso extremo en que β es opuesta a α, las probabilidades se hacen de 0% para «sí» y de 100% para «no». Por lo que es seguro que el resultado de la segunda medición será el contrario del correspondiente a la primera. (Véase Feynman et al, 1965, para más información sobre el spin).

La esfera de Riemann juega un papel fundamental (pero no siempre reconocido) en cualquier sistema cuántico de dos estados, describiendo el conjunto de estados cuánticos posibles (salvo proporcionalidad). Para una partícula de spin 1/2, su papel geométrico es particularmente evidente porque los puntos de la esfera corresponden a las posibles direcciones espaciales para el eje de giro. En otras situaciones es difícil observar ese papel. Consideremos un fotón que acaba de atravesar un par de rendijas, o que ha sido reflejado por un espejo semirreflectante. El estado del fotón es alguna combinación lineal tal como |ψ_m〉 + |ψ_i〉, |ψ_m〉 − |ψ_i〉 o |ψ_m〉 + i|ψ_i〉 de dos estados |ψ_m〉 y |ψ_i〉, los cuales describen dos localizaciones distintas. La esfera de Riemann describe todavía el conjunto de posibilidades físicamente distintas, pero ahora sólo de manera abstracta. El estado |ψ_m〉 está representado por el Polo Norte (cima) y |ψ_i〉 por el Polo Sur (fondo). Entonces, |ψ_m〉 + |ψ_i〉, |ψ_m〉 − |ψ_i〉 y |ψ_m〉 + i|ψ_i〉 están representados por los diversos puntos en el ecuador, y en general w|ψ_m〉 + z|ψ_i〉 está representado por el punto dado por q = z/w. En muchos casos, como éste, el «valor de posibilidades de la esfera de Riemann» está bastante oculto, como oculta queda su relación con la geometría espacial.