OBJETOS CON GRAN SPIN

Para un sistema cuántico en que el número de estados base es mayor que dos, el espacio de estados físicamente distinguibles es más complicado que la esfera de Riemann.

Sin embargo, en el caso del spin la propia esfera de Riemann tiene siempre por sí misma un papel geométrico directo que jugar. Consideremos una partícula o átomo en reposo con masa y de spin n × ℏ/2. El spin define entonces un sistema cuántico de (n + 1) estados. (Para una partícula sin masa que gira, es decir, una que viaje a la velocidad de la luz, tal como un fotón, el spin es siempre un sistema de dos estados como el descrito antes, pero para una partícula con masa el número de estados crece con el spin).

Si decidimos medir este spin en alguna dirección, encontramos que existen n + 1 diferentes resultados posibles, dependiendo de la cantidad del spin que se halle orientada a lo largo de dicha dirección. En términos de la unidad fundamental ℏ/2, los posibles resultados para el valor del spin en dicha dirección son n, n − 2, n − 4, …, 2 − n o n. Por lo cual, para n = 2 los valores son 2, 0 o −2; para n = 3, los valores son 3, 1, −1, o −3, etc. Los valores negativos corresponden al spin que apunta principalmente en la dirección opuesta a la que se está midiendo. El caso de spin 1/2, es decir n = 1, el valor 1 corresponde a «sí» y el valor −1 corresponde a «no».

Ahora bien, resulta, aunque no intentaré explicar las razones (Majorana, 1932; Penrose, 1987a), que todo estado de spin (salvo proporcionalidad) para spin ℏn/2 está caracterizado unívocamente por un conjunto (no ordenado) de n puntos en la esfera de Riemann —es decir, por n direcciones (habitualmente distintas) que salen del centro hacia afuera (véase figura VI.29)—. (Estas direcciones están caracterizadas por las mediciones que podríamos realizar en el sistema: si medimos el spin en una de ellas, es seguro que el resultado no estará completamente en la dirección opuesta, esto es, dará uno de los valores n, n − 2, n − 4, …, 2 − n, pero no −n). En el caso particular n = 1, como el electrón anterior, tenemos un punto en la esfera de Riemann, y éste es simplemente el punto caracterizado por q en las descripciones que hicimos.

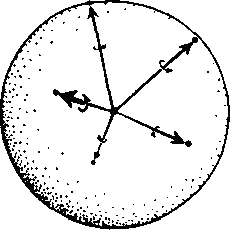
FIGURA VI.29. Un estado general de spin superior para una partícula con masa, puede describirse como una colección de estados de spin 1/2 apuntando en direcciones arbitrarias.

Pero para valores mayores del spin la imagen es más elaborada y es como la acabo de describir, aunque no es muy familiar a los físicos.

Hay algo enigmático en esta descripción. Frecuentemente se tiende a pensar que, en un sentido apropiado de límite, las descripciones cuánticas de los átomos (o las partículas elementales o las moléculas) coincidirán aproximadamente con las newtonianas clásicas cuando el sistema sea grande y complicado. Sin embargo, dicho así, esto es sencillamente falso porque —como hemos visto— los estados de spin de un objeto de gran momento angular corresponderán a un gran número de puntos salpicados por toda la esfera de Riemann.^[6.21]

Podemos considerar el spin del objeto como un lote completo de spines 1/2 apuntando en todas las direcciones que determinan estos puntos. Sólo algunos de esos estados combinados —a saber, aquellos en los que la mayoría de los puntos se concentran en una pequeña región de la esfera (es decir, en los que la mayoría de los spines y apuntan aproximadamente en la misma dirección)— corresponderán a los verdaderos estados de momento angular que encontramos normalmente con los objetos clásicos, como las bolas de cricket. Hubiéramos esperado que si escogemos un estado de spin para el que la medida total de éste es un número muy grande (en términos de ℏ/2), aunque al azar en todo lo demás, entonces empezara a emerger algo similar al spin clásico. Pero no es así como funcionan las cosas. ¡En general, los estados de spin cuánticos cuando el spin total es grande no se parecen en nada a los clásicos!

¿Cómo debe hacerse, entonces, la correspondencia con el momento angular de la física clásica? Aunque la mayoría de los estados cuánticos de spin grande no se parecen a los clásicos, ellos son combinaciones lineales de estados (ortogonales) cada uno de los cuales se parece a uno clásico. De algún modo se realiza automáticamente una «medición» en el sistema y el estado «salta» (con cierta probabilidad) a uno u otro de esos estados similares a los clásicos. La situación es análoga con otras propiedades del sistema clásicamente medibles, y no sólo el momento angular. Es este aspecto de la mecánica cuántica el que debe entrar en juego cuando se quiere que un sistema «alcance el nivel clásico». Antes de que podamos discutir los sistemas cuánticos «grandes» o «complicados», tendremos que poseer alguna noción acerca de la manera singular en que la mecánica cuántica trata los sistemas que incluyen más de una partícula.