LA TIERRA DE TOR'BLED-NAM

Imaginemos que hemos realizado un largo viaje a algún mundo lejano. Llamaremos a este mundo Tor'Bled-Nam. Nuestros sensores de detección remota han captado una señal que se muestra ahora en una pantalla frente a nosotros. La imagen se focaliza y vemos (figura III.1):

FIGURA III.1. Una primera impresión de un mundo extraño.

¿Qué puede ser? ¿Es algún insecto de extraña apariencia? Tal vez, en lugar de ello, sea un lago de color oscuro con muchas cadenas montañosas que se adentran en él. ¿O podría ser una inmensa ciudad extraterrestre con una forma extraña y con carreteras que salen en varías direcciones hacia las pequeñas ciudades y pueblos vecinos? Quizá sea una isla; tratemos entonces de descubrir si existe algún continente próximo al que está asociada. Podemos hacer esto «retrocediendo», reduciendo la amplificación de nuestro dispositivo sensor en un factor lineal de aproximadamente quince. Dicho y hecho, el mundo completo surge a la vista (figura III.2):

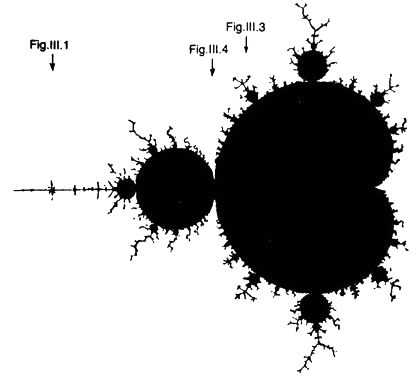
FIGURA III.2. «Tor'Bled-Nam» en su totalidad. Las localizaciones de las ampliaciones que se muestran en las figs. III.1, III.3 y III.4 son las indicadas bajo las flechas.

Nuestra «isla» se ve como un punto pequeño indicado bajo «figura III.1» en la figura III.2. Todos los filamentos (¿ríos, carreteras, puentes?) que parten de la isla original tienen un extremo final, con la excepción del que sale del interior de la grieta de su lado derecho, que acaba por unirse a un objeto mucho mayor que vemos representado en la figura III.2. Este objeto mayor es claramente similar a la isla que vimos primero, aunque no es exactamente igual. Si examinamos con mayor atención lo que parece ser la línea costera de este objeto vemos innumerables protuberancias —redondas—, si bien ellas mismas poseen sus propias protuberancias similares. Cada pequeña protuberancia parece estar unida a otra mayor en alguna región minúscula, dando lugar a una serie de verrugas sobre otras verrugas.

A medida que la imagen se hace más nítida, vemos miríadas de pequeñísimos filamentos que emanan de la estructura. Los propios filamentos se ramifican en varios lugares y a menudo serpentean de forma imprevisible. En ciertos puntos de los filamentos parecen apreciarse pequeños nudos de más complejidad que nuestro dispositivo sensor, con su amplificación actual, no puede resolver. Evidentemente el objeto no es una isla o continente real, ni ningún tipo de paisaje. Tal vez, después de todo, estamos viendo algún monstruoso escarabajo, y lo primero que vimos era parte de su prole, unida todavía a él por algún tipo de cordón umbilical filamentoso.

Tratemos de examinar la naturaleza de una verruga de nuestra criatura, aumentando la amplificación de nuestro dispositivo sensor en un factor lineal de aproximadamente diez (figura III.3 —cuya localización está indicada bajo «figura III.3» en la figura III.2—).

FIGURA III.3. Una verruga con una «quinariedad» en sus filamentos.

La propia verruga tiene un fuerte parecido con la criatura global —excepto sólo en el punto de unión—. Nótese que hay varios lugares en la figura III.3 en donde se juntan cinco filamentos. Hay quizá una cierta «quinariedad» en esta verruga particular (como habría una «ternariedad» en la verruga superior). De hecho, si examináramos la siguiente verruga de tamaño apreciable, hacia la parte inferior izquierda en la figura III.2, descubriríamos una «septenariedad» en ella; y una «nonariedad» en la siguiente, y así sucesivamente. A medida que nos adentramos en la grieta entre las dos regiones mayores de la figura III.2, encontramos verrugas a la derecha caracterizadas por números impares que incrementan de dos en dos. Examinemos más profundamente esta grieta, aumentando la ampliación de la figura III.2 en un factor de unos diez (figura III.4).

FIGURA III.4. La grieta principal. El «Valle de los caballos de mar» es apenas perceptible en la parte inferior Derecha.

Vemos otras numerosas verrugas minúsculas y también una agitada actividad. A la derecha, podemos distinguir algunas pequeñas «colas de caballo de mar» espirales —en un área que llamaremos «Valle de los caballos de mar»—. Aquí encontraremos, si la amplificación se aumenta lo suficiente, varias «anémonas de mar» o regiones con una apariencia floral diferente. Tal vez, después de todo, se trate realmente de alguna exótica línea costera —quizá algún arrecife coralino, con vida de todo tipo—. Lo que pudiera haber parecido una flor revelará, en una posterior ampliación, estar compuesto de miríadas de pequeñísimas aunque increíblemente complicadas estructuras, cada una con numerosos filamentos y colas espirales retorcidas. Examinemos con algún detalle una de las mayores colas de caballo de mar, a saber, la que es discernible donde se indica como «figura III.5» en la figura III.4 (que está unida a una verruga con una ¡«29-riedad»!). Con una posterior amplificación de 250 aumentos se nos presenta la espiral mostrada en la figura III.5.

FIGURA III.5. Un primer plano de una cola de caballo de mar.

Descubrimos que ésta no es una cola ordinaria sino que ella misma está formada por más complicados remolinos hacia uno u otro lado, con innumerables espirales minúsculas y regiones que semejan pulpos y caballos de mar.

En muchos lugares la estructura está entrelazada precisamente donde se juntan dos espirales. Examinemos uno de estos lugares (indicado bajo «figura III.6» en la figura III.5) incrementando nuestra amplificación en un factor de aproximadamente treinta.

FIGURA III.6. Una ampliación adicional de un punto de unión en el que se juntan dos espirales. Un pequeño bebé es apenas visible en el punto central.

¡Ya está!; ¿distinguimos un objeto extraño, aunque ahora familiar, en el centro? Una amplificación posterior en un factor de seis (figura III.7) revela una minúscula criatura bebé, ¡casi idéntica a la estructura global que hemos estado examinando!

FIGURA III.7. En una nueva ampliación se aprecia que el bebé se asemeja, mucho al mundo global.

Si miramos más de cerca vemos que los filamentos que emanan de ella difieren un poco de los de la estructura principal, y se retuercen y extienden hasta distancias relativamente mucho mayores. Pero la propia criatura minúscula apenas parece diferir de su progenitor, hasta el grado de poseer incluso su propia prole en posiciones estrechamente análogas. Podríamos examinarlas una vez más si quisiésemos aumentando la amplificación. Los nietos se parecerán también a su antepasado común, y ya nos sentimos dispuestos a creer que esto continúa indefinidamente.

Podemos explorar este extraordinario mundo de Tor'Bled-Nam hasta donde deseemos, ajustando nuestro dispositivo sensor a mayores y mayores grados de amplificación. Encontramos una variedad sin fin: no hay dos regiones que sean exactamente iguales, pero hay un aire general al que pronto nos acostumbramos. La ahora familiar criatura escarabajoide emerge en escalas más y más pequeñas. En todo momento las estructuras filamentosas vecinas difieren de las que habíamos visto antes, y se nos presentan fantásticas escenas nuevas de increíble complejidad.

¿Qué es esta extraña, variada y maravillosamente intrincada tierra con la que hemos topado? Sin duda muchos lectores ya lo sabrán, pero otros no. Este mundo no es más que un objeto de la matemática abstracta: el conjunto conocido como conjunto de Mandelbrot.^[3.1] Es complicado, sin duda; ¡pero está generado por una regla de notable simplicidad! Para explicar la regla adecuadamente tendré que explicar antes lo que es un número complejo. Eso es lo que voy a hacer ahora. Necesitaremos los números complejos más adelante. Son absolutamente fundamentales para la estructura de la mecánica cuántica y son, por consiguiente, básicos para el funcionamiento del propio mundo en que vivimos. También constituyen uno de los grandes milagros de la matemática. Para explicar lo que es un número complejo necesitaré antes recordar al lector lo que significa el término «número real». ¡Será útil, también, señalar la relación entre dicho concepto y la propia realidad del «mundo real»!