¿ES COMPUTABLE LA VIDA EN EL MUNDO DE LAS BOLAS DE BILLAR?

Permítaseme ilustrar primero, con un ejemplo absurdamente artificial, el hecho de que computabilidad y determinismo son diferentes, exhibiendo un «modelo de universo de juguete» que es determinista pero no computable. Describamos el «estado» del sistema en cualquier «instante» mediante un par de números naturales (m,n). Sea T_u una máquina universal de Turing bien determinada, por ejemplo la definida concretamente en el capítulo II. Para decidir cuál es el estado de este universo en el próximo «instante» debemos preguntar si la acción de T_u sobre m llegará a detenerse o no (es decir, si T_u(m) ≠ □ o T_u(m) = □ en la notación del capítulo II. Si se detiene, el estado en este próximo «instante» es (m + 1, n). Si no se detiene, será (n + 1, n). Vimos en el capítulo II que no existe algoritmo para el problema de la detención de la máquina de Turing. De ello se sigue que no puede haber algoritmo para predecir el «futuro» en este universo modelo, ¡a pesar de ser completamente determinista!^[5.14]

Por supuesto, este no es un modelo para tomar en serio, pero muestra que existe un problema. Podemos pedir a cualquier teoría física determinista que sea o no computable. De hecho, ¿es computable el mundo de las bolas de billar newtonianas?

El tema de la computabilidad física depende en parte del tipo de pregunta que nos propongamos plantearle al sistema. Puedo imaginar cierto número de preguntas que podrían plantearse y para las que mi conjetura sería que no son computables (esto es, que no es asunto algorítmico verificar la respuesta) en un modelo de bolas de billar newtonianas. Una de estas cuestiones podría ser: ¿choca alguna vez la bola A con la bola B? La idea es que se nos darían, como datos iniciales, las posiciones y velocidades de todas las bolas en cierto instante de tiempo (t = 0) y el problema consiste en calcular a partir de estos datos si las bolas A y B chocarán o no alguna vez en cualquier instante posterior (t > 0). Para hacer el problema más concreto (aunque no particularmente realista) podemos suponer que todas las bolas son del mismo radio y la misma masa y que hay, por ejemplo, una ley de fuerzas del tipo de la inversa del cuadrado actuando entre cada par de bolas.

Una razón para conjeturar que esta pregunta concreta no es de las que pueden resolverse algorítmicamente es que el modelo es en cierto modo semejante a un «modelo de bolas de billar para una computación» que fue introducido por Edward Fredkin y Tommaso Toffoli (1982). En su modelo (en lugar de tener una ley de fuerzas de la inversa del cuadrado) las bolas están limitadas por varias «paredes», pero rebotan elásticamente una sobre otra de modo semejante a como lo hacen las bolas newtonianas que acabo de describir (véase figura V.9).

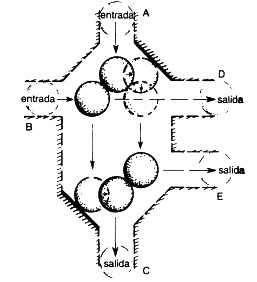
FIGURA V.9. Un conmutador (sugerido por A. Resler) en la computadora de bolas de billar de Fredkin-Toffoli. Si un bola entra por B, otra saldrá a continuación por D o por E dependiendo de si otra bola entra por A, en donde las entradas por A y B se suponen simultáneas.

En el modelo de Fredkin-Toffoli todas las operaciones lógicas básicas de un ordenador pueden ejecutarse mediante las bolas. Puede imitarse cualquier computación de una máquina de Turing: la elección particular de la máquina de Turing T_n define la configuración de las «paredes», etc., de la máquina de Fredkin-Toffoli; una vez hecho esto, un estado inicial de bolas codifica la información de la cinta de input, y la cinta de output de la máquina de Turing queda codificada en el estado final de las bolas. Así puede plantearse, en particular, la pregunta: ¿se parará alguna vez tal o cual máquina computadora de Turing? «Parada» puede entenderse como que la bola A choque finalmente con la bola B. El hecho de que esta cuestión no pueda ser resuelta algorítmicamente indica al menos que la pregunta newtoniana «¿choca alguna vez la bola A con la bola B?», que planteé inicialmente, tampoco podrá responderse algorítmicamente.

En realidad, el problema newtoniano es mucho más complicado que el desarrollado por Fredkin y Toffoli. Estos pudieron especificar los estados de su modelo conforme a parámetros discretos (es decir, mediante enunciados «si o no» como «o la bola está en el canal o no lo está»). Pero en el problema newtoniano completo las posiciones y velocidades de las bolas tienen que especificarse con precisión infinita según coordenadas que son números reales, y no en forma discreta.

De este modo, nos enfrentamos otra vez con todos los problemas que tuvimos que considerar cuando en el capítulo IV nos ocupábamos de la cuestión de si el conjunto de Mandelbrot es o no recursivo. ¿Qué significa «computable» cuando se admiten como datos de entrada y salida parámetros que varían de forma continua?^[5.15] Por el momento, el problema puede atenuarse suponiendo que todas las coordenadas de posición y velocidad iniciales vienen dadas por números racionales (aunque no podemos esperar que tales coordenadas sigan siendo racionales para posteriores valores racionales del tiempo t). Recordemos que un número racional es un cociente entre dos enteros; por consiguiente está definido en términos discretos finitos. Utilizando números racionales podemos aproximar, tanto como queramos, cualesquiera conjuntos de datos iniciales que hayamos decidido examinar. No es del todo descabellado conjeturar que, con datos iniciales racionales, pueda no existir algoritmo para decidir si finalmente chocarán las bolas A y B.

Sin embargo, esto no es realmente lo que queremos decir al afirmar que «el mundo de las bolas de billar newtonianas no es computable». El modelo particular que he estado comparando con nuestro mundo de bolas de billar newtonianas, a saber, la «computadora de bolas de billar» de Fredkin-Toffoli, actúa realmente de acuerdo con un cálculo. Éste, después de todo, era el punto esencial de la idea de Fredkin-Toffoli, que su modelo se comportara como una computadora (universal). El tipo de problema que trato de plantear es si es concebible que un cerebro humano pueda, aprovechando algunas leyes físicas «no computables», «superar» en algún sentido a una máquina de Turing. De nada sirve tratar de aprovechar algo como:

«Si la bola A nunca choca con la bola B entonces la respuesta a su problema es no».

¡Acaso habría que esperar indefinidamente para asegurar que las bolas en cuestión no chocan nunca! Este es, por supuesto, el modo en que se comporta una máquina de Turing.

Parece que, en efecto, hay claros indicios de que, en un sentido apropiado, el mundo de las bolas de billar newtonianas es computable (al menos si prescindimos del problema de los choques múltiples). Normalmente trataríamos de computar este comportamiento haciendo algunas aproximaciones. Podríamos imaginar que se especifica que los centros de las bolas están en una malla de puntos, en donde los puntos nodales de la malla son precisamente aquellos que miden las coordenadas (en centésimas de unidad, por ejemplo). El tiempo se considera también «discreto»: todos los instantes permitidos son múltiplos de alguna pequeña unidad (denotada por ∆t , por ejemplo). Esto plantea algunas posibilidades discretas para las «velocidades» (diferencias en los valores de la posición de los nodos en dos instantes permitidos sucesivos divididas por ∆t).

Las aproximaciones apropiadas para las aceleraciones se calculan utilizando la ley de fuerzas, y estas aceleraciones se utilizan para obtener las «velocidades» a partir de las que se calculan con el grado de aproximación requerido, las nuevas posiciones de los nodos en el próximo instante permitido. El cálculo continúa durante tantos intervalos temporales como sea posible mientras se mantenga la precisión deseada. Quizá no se puedan computar muchos instantes antes de que se pierda toda precisión. El método consiste entonces en empezar con una malla espacial considerablemente más fina y una división algo más fina de los instantes de tiempo permitidos. Esto permite alcanzar una mayor precisión y el cálculo puede llevarse más lejos que en el caso anterior antes de que se pierda la precisión. Con una malla espacial aún más fina, y una división más sutil de los intervalos de tiempo, la precisión puede aumentarse aún más y llevar el cálculo aún más lejos. De esta forma, el mundo de las bolas de billar newtonianas puede computarse tan concienzudamente como queramos (pasando por alto las colisiones múltiples) y, en este sentido, podemos decir que el mundo newtoniano es realmente computable.

Existe un sentido, no obstante, en el que este mundo es «no computable» en la práctica. Esto surge del hecho de que la precisión con que pueden conocerse los datos iniciales es siempre limitada. De hecho, existe una «inestabilidad» muy considerable inherente a este tipo de problemas. Un pequeñísimo cambio en los datos iniciales puede dar lugar rápidamente a un cambio absolutamente enorme en el comportamiento resultante. (¡Cualquiera que haya tratado de embuchacar una bola de billar americano, o pool, golpeándola con una bola intermedia que, a su vez, debe ser golpeada antes, sabrá lo que quiero decir!). Esto es particularmente evidente cuando se trata de colisiones (sucesivas), pero tales inestabilidades en el comportamiento pueden ocurrir también con la acción a distancia gravitatoria de Newton (con más de dos cuerpos). A menudo se utiliza el término «caos», o «comportamiento caótico», para este tipo de inestabilidad. El comportamiento caótico es importante, por ejemplo, en relación con el clima. ¡Aunque se conocen las ecuaciones newtonianas que gobiernan los elementos, las predicciones del tiempo a largo plazo son muy poco confiables!

Este no es en absoluto el tipo de «no computabilidad» que pueda «aprovecharse» de forma alguna. Consiste simplemente en que, puesto que hay un límite a la precisión con que puede conocerse el estado inicial, el estado futuro no puede ser computado confiablemente a partir del inicial. En efecto, se ha introducido un elemento aleatorio en el comportamiento futuro, pero esto es todo. Si el cerebro humano realmente recurre a los elementos no computables útiles que existen en las leyes físicas, éstos deben ser de un tipo completamente diferente, de un carácter mucho más positivo. Consiguientemente, no me referiré a este tipo de comportamiento «caótico» como «no computabilidad». Prefiero utilizar el término «impredecibilidad». La impredecibilidad es un fenómeno muy general en el tipo de leyes deterministas que aparecen en la física (clásica), como pronto veremos. ¡La impredecibilidad es algo que ciertamente, más que «aprovechar», nos gustaría minimizar al construir una máquina pensante!

Para ocuparnos de las cuestiones de computabilidad e impredecibilidad será conveniente adoptar un punto de vista más amplio que antes respecto a las leyes físicas. Esto nos facilitará el considerar no sólo el esquema de la mecánica newtoniana sino también las teorías posteriores que han venido a reemplazarla. Tendremos que echar una ojeada a la notable formulación hamiltoniana de la mecánica.