FIGURA 10.10. Variación del área y el volumen de una bola esférica en N dimensiones con radio igual a una unidad de longitud. El volumen tiene un máximo para N próximo a 5,3 pero luego decrece rápidamente.

A partir de esto vemos que las constantes de la Naturaleza tienen una influencia relativa mucho mayor cuando se trata de determinar los resultados de las leyes de la Naturaleza en tres dimensiones que la que tienen en universos con muchas más dimensiones espaciales.

El triste caso de Paul Ehrenfest

Ehrenfest no era solamente el mejor maestro en nuestra profesión que yo haya conocido; también estaba apasionadamente preocupado por el desarrollo y destino de los hombres, especialmente de sus estudiantes. Entender a los demás, ganar su amistad y confianza, ayudar a cualquiera enzarzado en luchas externas o interiores, animar el talento joven; todo esto era su elemento real, casi más que su inmersión en problemas científicos.

ALBERT EINSTEIN

Paul Ehrenfest era un santo Tomás dubitativo; pero era de sí mismo de quien dudaba. Era un físico austríaco de mucho talento que trabajó con muchos de los máximos nombres de la ciencia a principios del siglo XX: Einstein, Heisenberg, Schrödinger, Pauli, Dirac, todos se beneficiaron de su ayuda. Por encima de todo era un crítico incisivo, capaz de señalar los puntos débiles de cualquier argumento: la conciencia de la física. También era famoso por sus comentarios, como^[26]: «¿Por qué tengo tan buenos estudiantes? Porque yo soy muy estúpido». O «¿Usted dice eso por principio o sólo porque resulta que es cierto?».

Ehrenfest hizo importantes contribuciones a la física en varias áreas y los estudiantes de licenciatura que estudian mecánica cuántica llegan invariablemente al «teorema de Ehrenfest». Pero los niveles exigidos por Ehrenfest eran tan elevados que ni él podía estar a la altura. Su infancia había sido infeliz. Su madre murió en 1890, cuando él tenía diez años, y su padre, que había sufrido una mala salud crónica, murió seis años después.

A pesar de la alta estima en que otros lo tenían, y que le llevó a ser invitado a ocupar la cátedra de física en Leiden en 1912, cuando sólo tenía 32 años (figura 10.11), Ehrenfest sufría de baja autoestima. Llegó a estar frustrado por su incapacidad para seguir el rápido ritmo de los desarrollos en física cuántica y su Naturaleza cada vez más matemática. En mayo de 1931 escribió a Niels Bohr diciéndole:

He perdido por completo el contacto con la física teórica. No puedo leer nada más y me siento incompetente para tener siquiera la más modesta idea de lo que tiene sentido entre el diluvio de artículos y libros. Quizá ya no sirva para nada.

FIGURA 10.11. Paul Ehrenfest (1880-1933) con Albert Einstein^[27].

Su desesperación se ahondó, exacerbada por los graves problemas mentales de su hijo Wassik, con síndrome de Down. Ludwig Boltzmann, que fue supervisor de Ehrenfest, se había suicidado en 1906 desesperado por la falta de reconocimiento de su trabajo. Paul Ehrenfest hizo lo mismo el 25 de septiembre de 1933, pegándose un tiro después de haber disparado a su hijo en la sala de espera del médico. Su última carta de explicación a sus más íntimos amigos científicos y a sus estudiantes nunca fue enviada^[28].

Ehrenfest es parte de nuestra historia porque, en 1917, fue el primero en advertir^[29] cuántos aspectos de las leyes físicas dependían en gran manera del número de dimensiones del espacio. Desarrollando las ideas de Kant acerca de la conexión entre la ley de la inversa del cuadrado de la gravedad y las dimensiones del espacio, Ehrenfest advirtió que sólo era posible tener planetas moviéndose alrededor de una masa central (como el Sol) en órbitas estables si el mundo tenía tres dimensiones. Llevando esto a la escala de los átomos, donde la ley de la inversa del cuadrado de la electricidad y el magnetismo es responsable de la fuerza atractiva entre los núcleos atómicos cargados positivamente y los electrones cargados negativamente que se mueven a su alrededor, Ehrenfest demostró que en mundos con más de tres dimensiones no podían existir átomos estables en absoluto. O bien los electrones caían al núcleo en una trayectoria espiral o bien se dispersaban.

Ehrenfest advirtió también que las ondas tridimensionales tienen propiedades muy especiales. Sólo en tres dimensiones viajan las ondas en el espacio libre sin distorsión o reverberación. Si el número de dimensiones del espacio es par (dos, cuatro, seis…), entonces las diferentes partes de una perturbación ondulatoria viajarán a velocidades diferentes. Como resultado, si la emisión ondulatoria es continua habrá reverberación en el receptor: ondas que salen en instantes diferentes llegarán al mismo tiempo. Si el número de dimensiones del espacio es un número impar, todas las perturbaciones viajan a la misma velocidad, pero si no hay tres dimensiones la onda se distorsionará cada vez más. Las ondas tridimensionales son especiales.

El imaginativo estudio de Ehrenfest demostraba que la dimensionalidad del mundo tiene un efecto de largo alcance sobre cómo son las cosas. Los mundos tridimensionales son muy inusuales^[30]. Imponen propiedades especiales a las leyes y constantes de la Naturaleza.

Pese a todo, Ehrenfest no fue más lejos en 1917 y no extrajo conclusiones filosóficas especiales de sus resultados. No fue el primero en advertir que había algo especial en las órbitas planetarias en mundos tridimensionales. William Paley había explicado ya en 1802 las características únicas en apoyo a la ley inversa del cuadrado de la gravedad, y el examen que hizo Wallace en 1905 en El lugar del hombre en el Universo había reiterado estas características especiales. Pero estos autores habían escrito antes de que hubiera surgido la teoría cuántica de la materia y Ehrenfest podía hacer un razonamiento mucho más completo y más profundo sobre la singularidad física de los mundos tridimensionales.

El caso especial de Gerald Whitrow

El Universo es real, pero uno no puede verlo. Uno tiene que imaginarlo.

ALEXANDER CALDER^[31]

La conexión antrópica directa entre el número de dimensiones del espacio y la existencia de observadores vivos fue realizada por primera vez por el cosmólogo inglés Gerald Whitrow en 1955. Al plantear la cuestión «¿Por qué observamos que el Universo posee tres dimensiones?» trataba de ofrecer un nuevo tipo de respuesta^[32] argumentando que sólo podían existir observadores pensantes en mundos tridimensionales. De hecho, sugirió que sería posible deducir la dimensionalidad del mundo a partir del hecho de que nosotros, u otra forma de vida inteligente, existimos:

esta propiedad topológica fundamental del mundo… podría inferirse como el único concomitante natural de algunas otras características contingentes asociadas con la evolución de las formas superiores de vida terrestre, en particular del hombre, el formulador del problema.

Whitrow desarrolló sus argumentos en un libro de divulgación sobre cosmología publicado cuatro años después^[33] e intentó eliminar la posibilidad de un mundo bidimensional favorable para la vida argumentando que los inevitables cruces de conexiones entre células nerviosas en dos dimensiones cortocircuitarían la creación de una red neural compleja.

El enfoque de Whitrow es la primera aplicación de lo que ahora se llamaría el «principio antrópico». Es anterior a su aplicación por Dicke al problema de la G variable y a la hipótesis de los Grandes Números. Utilizando lo que sabemos hoy, podemos ampliarlo un poco más. Y si vamos a considerar qué sería el mundo si sus leyes continuaran siendo las mismas pero el número de dimensiones del espacio fuera diferente, ¿por qué detenernos allí? ¿Por qué no preguntar qué sucedería si el número de dimensiones del tiempo también fuera diferente^[34]?

La posibilidad de universos con diferentes dimensiones tanto de espacio como de tiempo ha sido explorada por varios científicos^[35]. Igual que hicimos cuando consideramos universos con otras dimensiones de espacio y una dimensión de tiempo, podemos suponer que las leyes de la Naturaleza mantienen la misma forma matemática pero permitir que el número de dimensiones del espacio y el tiempo recorran libremente todas las posibilidades. La situación está resumida en la imagen que se muestra^[36] en la figura 10.12.

La tabla de chequeo de todas las posibilidades puede reducirse drásticamente mediante la imposición de un pequeño número de requisitos razonables que parece probable que sean necesarios para que exista procesamiento de información, memoria, y por consiguiente vida. Si queremos que el futuro esté determinado por el presente, eliminamos todas las regiones de la tabla marcadas como «impredecible». Si queremos que existan átomos estables junto con órbitas estables de cuerpos (planetas) alrededor de estrellas, tenemos que recortar las franjas marcadas como «inestable». Recortando los mundos en los que hay sólo señalización más rápida que la luz, nos quedamos con nuestro propio mundo de 3 + 1 dimensiones de espacio más tiempo, junto con mundos muy simples que tienen 2 + 1, 1 + 1 y 1 + 2 dimensiones de espacio más tiempo. Normalmente se piensa que tales mundos son demasiado simples para contener seres vivos. Por ejemplo, en mundos 2 + 1 no hay fuerzas gravitatorias entre masas y hay una simplicidad impuesta a los diseños que desafía cualquier intento de desarrollar complejidad.

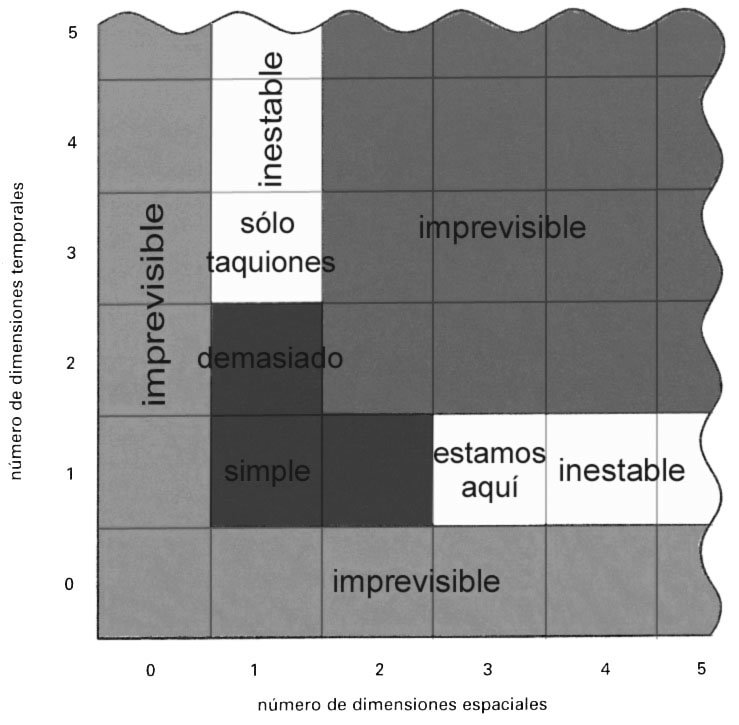
FIGURA 10.12. Las propiedades de universos con diferente número de dimensiones de espacio y tiempo. Un tiempo y tres dimensiones de espacio parece tener propiedades especiales que son necesarias para que existan estructuras tan complejas como seres vivos.

Independientemente de estas limitaciones, ha habido mucha especulación sobre cómo podrían construirse artefactos que funcionen en mundos bidimensionales^[37]. Ya hemos mencionado el interés de Whitrow en producir complejidad neural adecuada en un mundo bidimensional. Las redes son extremadamente limitadas porque los caminos no pueden cruzarse sin cortarse^[38].

Mundos con más de un tiempo son difíciles de imaginar y parecen ofrecer muchas más posibilidades. Desgraciadamente parecen ofrecer tantas posibilidades que las partículas elementales de materia son mucho menos estables que en mundos con una única dimensión temporal. Los protones pueden desintegrarse fácilmente en neutrones, positrones y neutrinos, y los electrones pueden desintegrarse en neutrones, antiprotones y neutrinos. El efecto global de dimensiones temporales extra es hacer altamente inestables las estructuras complejas a menos que estén congeladas en condiciones de temperatura extremadamente baja^[39].

Cuando consideramos mundos con dimensiones de espacio y tiempo distintas de 3 + 1 topamos con un problema sorprendente. Los mundos con más de una dimensión no permiten predecir el futuro a partir del presente. En este sentido son más bien como mundos sin dimensión temporal. Un sistema organizado complejo, como el necesario para la vida, no podría utilizar la información recogida en su entorno para conformar su comportamiento futuro. Seguiría siendo simple: demasiado simple para almacenar información y evolucionar.

Si el número de dimensiones de espacio y tiempo hubiera sido escogido aleatoriamente y todos los números fueran posibles, entonces esperaríamos que el número fuera muy grande. Es muy improbable escoger un número pequeño. Sin embargo, las ligaduras impuestas por la necesidad de tener «observadores» para hablar del problema significa que no todas las posibilidades están disponibles y que se nos impone un espacio tridimensional. Todas las alternativas estarían privadas de vida. Si científicos de otro Universo conociesen nuestras leyes pero no el número de dimensiones en que vivimos, podrían deducir su número simplemente a partir del hecho de nuestra existencia.

En resumen, hemos visto que la aproximación de Whitrow al problema de por qué el espacio tiene tres dimensiones lleva a una estimación de gran alcance de cómo y por qué son peculiares los mundos tridimensionales con una única flecha del tiempo. Las alternativas son demasiado simples, demasiado inestables o demasiado impredecibles para que observadores complejos evolucionen y perduren dentro de ellos. Como resultado, no debería sorprendernos encontrarnos viviendo en tres dimensiones espaciales sujetos a los caprichos de un único tiempo. No hay alternativa.

El extraño caso de Theodor Kaluza y Oskar Klein

Los dogmas del pasado apacible son inadecuados para el tormentoso presente. La ocasión está llena de dificultades y debemos superamos. Puesto que nuestro caso es nuevo, también debemos pensar de nuevo y actuar de nuevo. Debemos desencantamos.

ABRAHAM LINCOLN

Theodor Kaluza (1885-1954) fue el único hijo de una familia de estudiosos que había vivido durante más de tres siglos en lo que entonces^[40] era la ciudad alemana de Ratibor. Su padre, Max, era un reputado estudioso de la lengua y literatura inglesas, pero Theodor manifestó un temprano talento para las matemáticas y se matriculó como estudiante en la Universidad de Königsberg, donde se doctoró en 1910. Hasta aquí, el joven Kaluza parecía estar listo para una carrera como profesor universitario e investigador de éxito. Era un hombre afable con amplios intereses y buen sentido del humor que hablaba y escribía en quince lenguas, pero que evidentemente no estaba muy dotado para las cosas prácticas de la vida. Su hijo nos cuenta algo revelador sobre su forma de enfocar las cuestiones prácticas. Cuando Theodor tenía poco más de veinte años decidió aprender a nadar. Consiguió un libro sobre natación, lo leyó cuidadosamente, se lanzó al agua y nadó con éxito en su primer intento. Tal era, afirmaba, el poder del conocimiento teórico.

Pero por alguna razón la carrera de Kaluza encalló. En lugar de permanecer, como otros jóvenes científicos de talento, durante sólo dos o tres años en un puesto de ayudante en la universidad, se quedó allí durante veinte años, sin conseguir nunca la promoción a una cátedra.

Durante este largo aprendizaje decidió escribir a Einstein a propósito de sus nuevas ideas referentes a la electricidad, el magnetismo y la gravedad. Esto sucedía en abril de 1919 y Einstein ya era reconocido entre los físicos por su trabajo sobre relatividad, gravedad y física atómica, aunque para el gran público todavía no era un nombre familiar. Kaluza había advertido que añadiendo una dimensión espacial extra al mundo se hacía posible unir la teoría de la gravedad de Einstein con la teoría de la electricidad y el magnetismo de Maxwell de forma muy económica. Einstein se tomó mucho tiempo para responder a la carta de Kaluza pero finalmente respondió con entusiasmo, urgiéndole a preparar el trabajo para su publicación. Einstein añadió su imprimatur comunicando el trabajo al Journal of the Prussian Academy^[41] en diciembre de 1921.

La idea de Kaluza era ciertamente espectacular. El electromagnetismo, afirmaba, era realmente igual que la gravedad propagándose en una dimensión espacial extra.

Pero aunque la teoría era matemáticamente muy elegante, tenía que enfrentarse a una difícil pregunta: «Si hay una dimensión extra del espacio ¿por qué no sentimos sus efectos?». Kaluza no abordó esta difícil cuestión en absoluto.

Una respuesta a este enigma fue ofrecida en 1926 por el físico matemático sueco Oskar Klein (1894-1977), uno de los antiguos estudiantes de Kaluza. Klein había desarrollado ideas bastante similares a las de Kaluza, pero las dejó de lado cuando vio que Kaluza se le había adelantado. Había escrito a Niels Bohr que «el origen de la constante de Planck podría buscarse en la periodicidad de la quinta dimensión^[42]» Era sencillo. La dimensión espacial extra es extraordinariamente pequeña y circular (aproximadamente 10⁻³⁰ centímetros de circunferencia) y, por lo tanto, su presencia es imperceptible. La constante de estructura fina de la Naturaleza que vemos en tres dimensiones toma un valor numérico que está controlado por el tamaño de la dimensión extra.

Esta teoría de Kaluza-Klein, como llegó a conocerse, fue de interés durante cierto tiempo, pero luego desapareció hasta la década de 1980, cuando reemergió para convertirse en un foco de interés para los físicos.

La teoría de Kaluza y Klein mostró a los físicos que el mundo podía tener dimensiones espaciales extra sin adolecer de los problemas que Ehrenfest y otros habían demostrado que eran endémicos en mundos con más de tres dimensiones. El truco consistía simplemente en que la dimensionalidad tenía que ser antidemocrática: podía haber más de tres dimensiones espaciales pero tenían que ser pequeñas e invariables para no alterar el carácter del mundo que experimentamos. Las fuerzas de la Naturaleza no deben propagar democráticamente sus influencias en todas las dimensiones: las dimensiones espaciales extra tenían que ser mucho menores en extensión que las tres que nos son familiares.

En la década de 1980 los físicos empezaron a resucitar las ideas de Kaluza y Klein para ver si añadiendo aún más dimensiones sería posible unir las fuerzas fuerte y débil de la Naturaleza con el electromagnetismo y la gravedad. Si pudiera hacerse que esta idea funcionara, entonces las constantes de la Naturaleza que describían las intensidades de estas fuerzas estarían determinadas por el tamaño de cada una de las dimensiones responsables. Durante un tiempo pareció que esta nueva idea podría funcionar. Se hicieron intentos serios de calcular el valor de la constante de estructura fina en teorías con dimensiones extra^[43].

Pero poco a poco empezaron a manifestarse los fallos. Las simples dimensiones extra de Kaluza y Klein no podían imitar todas las complicadas propiedades de las fuerzas fuerte y débil de la Naturaleza ni acomodar las propiedades de las particulares partículas elementales que gobernaban. No obstante, las lecciones aprendidas de esta aproximación fueron importantes y pudieron aplicarse a las nuevas teorías de supercuerdas que reparaban los defectos de las teorías de Kaluza-Klein, como veremos. Lo más importante era que cuando abrimos nuestra mente a la posibilidad de que el mundo posea más de tres dimensiones espaciales, entonces las verdaderas constantes de la Naturaleza deben vivir en el número total de dimensiones. Las sombras de ellas que vemos en nuestro mundo tridimensional pueden tener un valor muy diferente y, lo más chocante de todo, ni siquiera tienen que ser constantes.

Kaluza consiguió finalmente una cátedra, primero en Kiel en 1929 y luego en Gotinga en 1935, después de que Einstein apoyase por escrito su nombramiento.

En su recomendación llamaba especialmente la atención sobre la novedad de su intento de unir gravedad y electromagnetismo con dimensiones extra.

Constantes variables en la brana

Hay dos maneras de difundir la luz: ser la vela o el espejo que la refleja.

EDITH WHARTON^[44]

La consecuencia más interesante de añadir dimensiones espaciales extra es que permite que cambien las constantes de la Naturaleza observadas. Si el mundo tiene realmente cuatro dimensiones espaciales, entonces las verdaderas constantes de la Naturaleza existen en cuatro dimensiones. Si nosotros nos movemos sólo en tres de esas dimensiones, veremos o sentiremos sólo «sombras» tridimensionales de las auténticas constantes tetradimensionales. Pero esas sombras no tienen por qué ser constantes. Si la dimensión extra aumenta en tamaño, igual que se están expandiendo nuestras tres dimensiones del Universo, entonces nuestras constantes tridimensionales decrecerán al mismo ritmo. Esto nos dice inmediatamente que si algunas dimensiones extra están cambiando, deben hacerlo de una forma bastante lenta; de lo contrario no las hubiéramos llamado «constantes» en absoluto.

Tomemos una constante tradicional de la Naturaleza, como la constante de estructura fina. Si el tamaño de la dimensión extra^[45] del espacio es R, entonces el valor de la «constante» de estructura fina tridimensional, α, variará en proporción a 1/R² cuando cambia R. Imaginemos que estamos en un Universo en expansión de cuatro dimensiones pero sólo podemos movemos en tres de ellas. Las fuerzas de la electricidad y magnetismo pueden «ver» las cuatro dimensiones y encontraremos que nuestra parte tridimensional de ellas se debilitará cuando la cuarta dimensión se haga mayor.

Sabemos que si la constante de estructura fina tridimensional está cambiando no puede hacerlo en ninguna parte tan rápido como se expande el Universo. Esto nos dice que cualquier cuarta dimensión debe ser muy diferente de las otras. La idea de Klein consistía en que es a la vez muy pequeña y estática. Alguna fuerza extra atrapa las dimensiones extra y las mantiene pequeñas. Si no cambian de tamaño de forma significativa no tenemos por qué ver que ninguna de nuestras constantes esté variando hoy. Un escenario posible imagina que el Universo empieza con todas sus dimensiones espaciales comportándose de una manera democrática, pero luego algunas de las dimensiones quedan atrapadas y permanecen estáticas y pequeñas desde entonces, dejando sólo tres para hacerse grandes, expandiéndose hasta convertirse en el Universo astronómico que observamos hoy (ver figura 10.13).

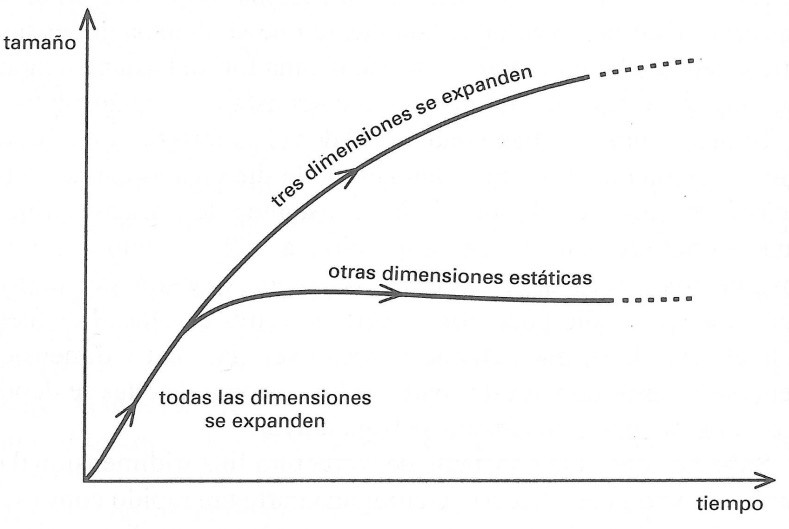
FIGURA 10.13. Un escenario en que el Universo empieza con más de tres dimensiones espaciales en expansión antes de sufrir un cambio hacia un estado en el que sólo tres siguen expandiéndose mientras las demás quedan atrapadas y estáticas.

En 1982, los teóricos de cuerdas sugirieron por primera vez una respuesta espectacular a un viejo problema: cómo casar la teoría cuántica de la materia con la teoría de la gravedad de Einstein. Todos los intentos previos habían fracasado miserablemente. Predecían invariablemente que alguna cantidad medida debería ser infinita^[46]. Estos «infinitos» plagaban todas las teorías con sólo tres dimensiones de espacio y una de tiempo. Pero en 1984 Michael Green y John Schwarz demostraron que este problema podía subsanarse combinando dos ideas radicales. Si se abandona la idea de que las entidades más básicas son puntuales, con tamaño cero, y se permite que haya más de tres dimensiones espaciales, entonces los infinitos desaparecen milagrosamente, cancelándose. Como sucede con las anteriores teorías de Kaluza-Klein, estas dimensiones extra no pueden estar cambiando hoy de forma significativa o veríamos cambios en las «constantes» de la Naturaleza que gobiernan la estructura de nuestro mundo tridimensional. De nuevo, se suponía que están atrapadas por fuerzas desconocidas en una escala muy pequeña, cerca de la escala de longitud fundamental de Planck de 10⁻³³ cm.

La simple idea de que sólo tres de las dimensiones del espacio toman parte en la expansión del Universo ilumina los misterios centrales sobre las dimensiones del espacio y el tiempo. Estamos descubriendo que las teorías de cuerdas seleccionan números especiales de dimensiones de espacio y tiempo juntos. No se ha encontrado en dichas teorías ninguna razón por la que sólo una de las dimensiones espacio-temporales especificadas en números sea un tiempo; ni por qué tres dimensiones se han hecho grandes. Si las otras están confinadas en una extensión muy pequeña, entonces necesitamos saber si tenían que ser tres dimensiones las que se hicieron grandes o si este número salió al azar y podían haber sido diferentes. Si el número de dimensiones espaciales se escogió al azar por la forma en que se desarrollaron los sucesos cerca del comienzo de la expansión del Universo, entonces podría haber un número diferente de dimensiones grandes en otro lugar del Universo más allá de nuestro horizonte. Una elección aleatoria significaría que este aspecto del mundo no permitía ninguna explicación adicional en el sentido reduccionista normal: sólo en mundos con tres dimensiones de espacio y una de tiempo estaríamos aquí para advertir el hecho.

Recientemente ha surgido otro enfoque del problema de las dimensiones y las constantes. En lugar de que las dimensiones extra estén simplemente atrapadas de modo que no puedan cambiar, permite que sólo la gravedad tenga influencia sobre todas las dimensiones del espacio. Las otras tres fuerzas básicas de la Naturaleza están confinadas a actuar solamente en tres de las dimensiones, en una parte del Universo total en la que habitamos llamada la «mundobrana» (ver figura 10.14), así llamada por ser similar a una membrana multidimensional.

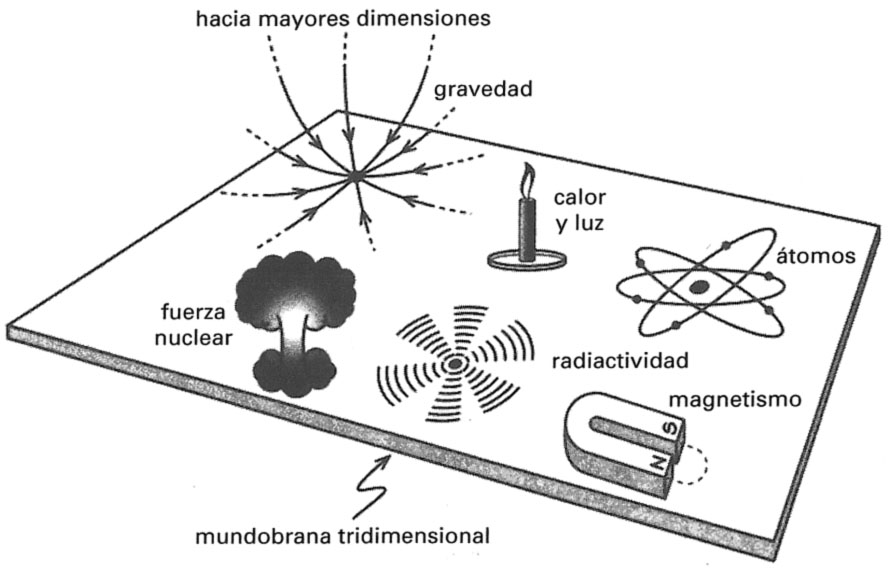
FIGURA 10.14. Las fuerzas de la Naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un «mundobrana» tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil.

El alcance multidimensional de la fuerza de la gravedad en las dimensiones superiores del espacio, lo que se llama el «volumen», es responsable de su relativa debilidad (por el famoso factor 10⁴⁰ de Eddington) comparada con las otras fuerzas que extienden sus «líneas» de fuerza a través de tres de las dimensiones. En este momento los mundobranas están sujetos a una intensa investigación de papel y lápiz por físicos de todo el mundo para ver si pueden dejar algún residuo decisivo en el Universo que permitiera una comprobación observacional. En los próximos años estas investigaciones quizá revelen la conexión entre las constantes de la Naturaleza que definen el verdadero espacio de dimensiones superiores en el que existen y los valores de sus sombras tridimensionales que gobiernan la evolución de la brana tridimensional que constituye todo lo que conocemos del verdadero Universo. Nuestras constantes estarán ligadas a los tamaños relativos de nuestro mundobrana y al volumen no observado del espacio de dimensiones superiores. Quizá estemos en el umbral de algún profundo descubrimiento que coloque a todo nuestro Universo visible en algún lugar del hiperespacio.