Capítulo 2

La gran verdad de la inversión: rentabilidad y riesgo

 

En este capítulo

   Cómo calcular la rentabilidad de tus inversiones

   Qué es el riesgo y cómo se cuantifica

   Valor del dinero en el tiempo (VDT)

 

“La gente subestima la importancia de unas pocas buenas

ideas simples. La lección es que unas pocas buenas ideas simples lealmente funcionan.”

 

CHARLIE MUNGER

Si has leído la introducción, sabrás que he prometido ayudarte a invertir tus ahorros sin que tengas que aprender fórmulas matemáticas ni complejos conceptos de economía, lo que no quita que tanto unas como otros deban aparecer en un momento u otro de este libro. Por ejemplo en este capítulo, que es en el que hay más matemáticas de todo el libro. Pero no te asustes, no tengo un especial interés en que te aprendas las fórmulas o su aplicación. El esfuerzo que te pido es mucho más simple: quédate con los conceptos. En estas páginas encontrarás los conceptos base de las finanzas y te servirán en todas las decisiones de inversión que tomes.

Este capítulo, pues, es fundamental porque, a la hora de invertir, más allá de los productos, los adornos y la película que te cuenten, todo se reduce a valorar dos dimensiones:

Y da igual si hablamos de invertir en acciones de Telefónica, en bonos del Estado o en apartamentos en la costa... ¿Qué rentabilidad esperas y qué riesgo vas a asumir a cambio?

Si la parte numérica de la inversión se te hace muy cuesta arriba, no te preocupes. El gran Warren Buffett (considerado uno de los mejores inversores de todos los tiempos y a quien dedicamos todo el capítulo 18) dijo una vez: “Si el cálculo o el álgebra fuesen imprescindibles para ser un buen inversor, tendría que volver a ser repartidor de periódicos”. En todo caso, no olvides el trato que acabamos de hacer: solo tendrás que aprenderte los conceptos.

La palabra fascinante: rentabilidad

Antes de adentrarnos en este capítulo, creo que estamos de acuerdo en que la rentabilidad es el beneficio que obtienes por el dinero que inviertes. ¿Y cuál es el valor de esa rentabilidad? Seguro que estás pensando: “¡Venga, hombre! ¿Cómo no voy a saber la rentabilidad de mi inversión si me la pone el banco en la información que me envía?”. Pues bien, ¿quieres que nos apostemos algo? Te acepto la apuesta. Y vas a perder.

Lo más intuitivo: la rentabilidad simple

Imagina que hace un año compraste una acción a 25 euros que hoy vale 30 euros. A la cuenta de la vieja has ganado 5 euros sobre una inversión de 25:

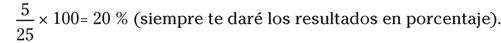
Acabas de aplicar el cálculo de rentabilidad simple. Si es una acción, seguramente te habrán pagado un dividendo (en el capítulo 5 verás qué es esto de los dividendos). Supón que te han pagado 0,10 euros de dividendo, pues prepárate que aquí llega una formulita que te valdrá para cualquier cálculo.

Un poco más sofisticado: la rentabilidad compuesta

Ahora supón que vas a un banco y te ofrece un depósito a plazo fijo al 6 % a un año. Como ya sabes calcular la rentabilidad simple, es fácil, pones 100 euros y dentro de un año tendrás 106.

Pero vas a otro banco y te ofrece algo nuevo. Te dice que también te paga un 6 % a un año pero con rentabilidad compuesta trimestral. Lo que te están diciendo es que los intereses no te los pagarán a un año, sino que el banco los liquidará cada trimestre y se irán sumando a la base de cálculo (recuerda el interés compuesto del capítulo 1). Veamos cómo se calcula:

Rentabilidad compuesta:

Cn = Co × (1 + I_m)^{T x m}

Donde:

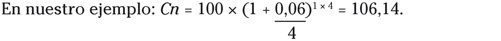
El “0,06” es el tipo de interés expresado en tanto por uno, que es la forma que se utiliza para hacer cálculos. Un 15 % expresado en tanto por uno sería 0,15, un 3 % expresado en tanto por uno es 0,03. La frecuencia “m” es de cuatro, ya que el banco nos liquida intereses de forma trimestral, es decir, cuatro veces al año.

Et voilà!, la magia del interés compuesto. Pagándonos lo mismo, un 6 % anual, el hacerlo con interés compuesto en lugar de simple hace que nuestra rentabilidad mejore y pase de un 6 a un 6,14 %.

Cuanto mayor sea la frecuencia de capitalización (las veces que te pagan los intereses durante la vida de tu inversión) más alta será la rentabilidad efectiva. Al 6,00 % anual que te pagan los dos bancos de los ejemplos anteriores se le llama Tipo de Interés Nominal, que verás en la publicidad de los bancos como TIN. Al tipo de interés que realmente obtienes (el 6,14%) se le llama Tipo de Interés Efectivo o TIE, y, por si querías más conceptos de tres letras, recuerda que, cuando contrates un depósito, las entidades tienen la obligación legal de darte la TAE, Tasa Anual Equivalente. La TAE indica la rentabilidad efectiva de un depósito (el TIE) incluyendo el impacto de las comisiones y los gastos (en la práctica no se suelen aplicar gastos y comisiones a un depósito o imposición a plazo fijo, por lo que la TIE casi siempre coincide con la TAE).

Cuando evalúes distintas ofertas bancarias para tus depósitos debes invertir en el que te ofrezca la TAE más alta... siempre y cuando la inversión sea al mismo plazo o similar. El cálculo de la TAE parte de la hipótesis de que los intereses pagados se reinvertirán al mismo tipo que el interés del depósito durante un año y eso, en la vida real, no funciona así. Una oferta tipo “depósito a tres meses TAE 3,25%” puede estar muy bien, pero fíjate en que la normativa legal obliga a dar el calculo anualizado (tasa anual) como si el depósito fuese a durar un año, independientemente de cuál será su vencimiento real. Así que ojo con comparar un depósito a tres meses con un depósito a un año. No funciona. Compara depósitos con el mismo plazo.

¿Te acuerdas del ca-rre-te?

Ya has visto dos formas de calcular la rentabilidad: la forma básica o rentabilidad simple y la compuesta. Todavía quedan algunas fórmulas por ver, y lo cierto es que a partir de aquí se complica un poco la cosa (solo un poco). En medio de tanta fórmula, me gustaría recordarte el famoso “carrete”, que es lo que, al fin y al cabo, utilizan en los bancos cuando te liquidan los intereses, tanto de las imposiciones a plazo fijo como de los créditos.

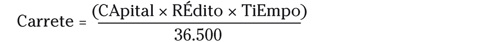
(La cifra de 36.500 del denominador se explica porque el 100 del porcentaje del crédito se multiplica por los 365 días del año.)

Supón una imposición a plazo fijo de 3.000 euros que te paga el 5 % a 90 días. La forma de calcularla sería:

Si eres un lector dummy perspicaz, te darás cuenta de que no te acaba de cuadrar: si te pagan el 5 % anual sobre 3.000 euros, son 150 euros anuales; como 90 días es un trimestre, una cuarta parte del año, si divido 150 entre 4 el resultado es 37,5 euros, entonces, ¿por qué salen 36,98 en nuestro cálculo?

Por el cambio de base. Es un concepto algo complejo y, si te pierdes con la explicación, no importa, es una herramienta de nivel profesional, aunque su lógica es básica: si un banco te aplica como base el año natural, puede perfecta y legalmente aplicar 365 días, lo que supone un divisor de 36.500, pero si aplica el año comercial, son 360 días, esto es, 36.000. Pudiera ser, y solo digo pudiera ser, que, cuando te liquiden un crédito, la base sea el año comercial (denominador menor, es decir, menos base, por lo tanto, resultado mayor, o sea, más intereses para el banco) y que cuando te paguen los intereses de una cuenta de ahorro a plazo fijo utilicen el año natural, 36.500 (denominador mayor, o sea, resultado más pequeño y, por lo tanto, menos intereses para ti). ¿Creías que los bancos son tontos o qué?

Cómo calcular la rentabilidad durante varios periodos

Ya hemos visto cómo calcular la rentabilidad simple de un periodo (un año, por ejemplo). Pero si tu inversión dura varios periodos y tienes la rentabilidad simple de cada uno, es muy sencillo calcular la rentabilidad total. Simplemente debes multiplicar (en tanto por uno, no te olvides) la rentabilidad de cada año.

Así, si en tres años has obtenido un 10 un 12 y un 6 % (en tanto por uno, 0,10, 0,12 y 0,06), tu rentabilidad acumulada es del:

R = [(1 + 0,10) × (1 + 0,12) × (1 + 0,06)] – 1 = 0,30592, y en porcentaje 30,59 %

Esta forma de mostrar la rentabilidad es válida, aunque tiene sus inconvenientes. De hecho, cuando veamos los fondos de inversión (llegaremos a ellos en el capítulo 20) verás que uno de los datos que se dan es la “rentabilidad acumulada de los últimos tres años”, en este caso, el 30,59 %. Pero los datos acumulados tienen una pega: no nos sirven para hacer demasiadas previsiones. Por ejemplo, hay periodos de cinco años en los que la bolsa ha arrojado ganancias acumuladas del 80 % y más, y otros en los que ha arrojado pérdidas acumuladas del 70 % y más.

Estos bloques de rentabilidades acumuladas de varios años son poco manejables, y no podemos utilizarlos para hacer previsiones basadas en probabilidades.

Rentabilidad media aritmética

Pensaba Aristóteles que la virtud consiste en saber encontrar el término medio entre dos extremos, y así debes ver la rentabilidad media aritmética.

La rentabilidad media aritmética es, simplemente, la suma de las rentabilidades dividida por el número de observaciones. Por ejemplo: mi cartera a lo largo de cinco años ha arrojado un 12, un 8, un 7, un –10 y un 3,5 %. La rentabilidad media aritmética será:

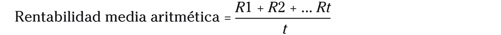
donde R1 es la rentabilidad del año 1, etc., y t el tiempo en años.

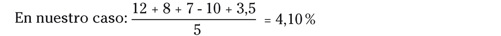
Recuerda este concepto, pues es una de las bases de la gestión de carteras que verás en el capítulo 16.

La media aritmética es una forma óptima de medir la rentabilidad media que has obtenido en un periodo de tiempo concreto. Además, es uno de los dos componentes básicos en la teoría moderna de carteras (te mueres por saber qué es eso, lo sé, pero paso a paso. Si no puedes esperar, consulta el capítulo 16).

Sin embargo, ¿estás seguro de que es una forma óptima para calcular la rentabilidad a lo largo del tiempo?

Vamos a comprobarlo con un ejemplo: supongamos que inviertes 100 euros y lo haces tan bien que el primer año ganas un 50 %. El segundo año la cosa pincha y pierdes un 50 %. Tu rentabilidad parece que sería nula, es decir, del 0 %, porque (+50 + –50) / 2 = 0. Lo comido por lo servido. Pues intenta ir a sacar los 100 euros que pusiste... ¡no los tienes! Solo te quedan 75 euros. Efectivamente, es así: invertiste 100 euros, ganaste un 50 %, por lo que tu saldo era de 150 euros (100 + 50), y luego esa inversión cayó un 50 %, por lo que tienes 75 euros (150 – 75). La media aritmética está bien calculada y no tiene ningún secreto, pero no muestra la realidad de lo que ha pasado.

Veámoslo con un ejemplo un poco más complejo. Supón una inversión con fuertes movimientos en su rentabilidad en la que has invertido 100 euros hace tres años. El primer año pierdes un 70 %, el segundo ganas un 266,67 % y el tercero pierdes un 54,55 %.

Es un valor que se mueve mucho, pero te ha ido muy bien. Tu gestor bancario te ha explicado que la rentabilidad media de la cartera es de nada más y nada menos que de un 47,37 % (–70 + 266,67 – 54,55 / 3). ¡Champán para todos! Un 47,37 % de rentabilidad media dobla la que consiguen los mejores gestores de carteras del mundo.

Pero tras el champán viene la resaca. Como puedes ver en la tabla 2-1, pusiste 100 euros y acabas con 50. ¿Qué ha ocurrido? Pues exactamente lo mismo que has visto en el caso más sencillo del +50 y del –50. La rentabilidad media aritmética da un resultado que no tiene nada que ver con la rentabilidad real que has obtenido.

Está claro que la rentabilidad media aritmética no muestra de forma adecuada la evolución de una inversión a lo largo del tiempo.

Rentabilidad media geométrica

La forma correcta de medir la rentabilidad de una inversión a lo largo del tiempo es a través de la media geométrica, y hay dos formas de calcularla:

La forma de interpretar estos datos es que nuestra inversión nos ha dado una pérdida anual compuesta del 20,63 % anual.

Para obtener la rentabilidad real de tu inversión debes aplicar la rentabilidad media geométrica, también llamada rentabilidad compuesta media. Y no te asustes, que no estás solo a la hora de hacer estos cálculos, ya que las hojas de cálculo de Excel te proporcionarán la forma automática de hacerlo a través de la función geomean; las calculadoras financieras están programadas para ello.

La regla del 72

Por el momento, vamos a dejar de lado las fórmulas complejas y te voy a explicar un pequeño truco que te permitirá saber rápidamente cuánto tiempo necesitas mantener una inversión para doblar tu capital ¿Quién no quiere doblar su capital?

Hay una curiosidad matemática con el tipo de interés compuesto y es que, haciendo un cálculo simple con el número 72, podemos determinar el número de años que necesitamos para doblar nuestra inversión.

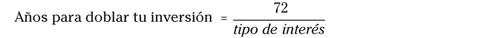
Así, si tu inversión crece al 4 % anual, la doblarás en 18 años (72 / 4), pero si consigues que crezca al 12 % podrías conseguirlo en 6 años (72 / 12).

Y si doblar te parece poco no hay problema, también tengo la regla del 115 para quien quiera jugar fuerte y triplicar su dinero. Tienes que hacer el mismo cálculo pero sustituyendo el 72 por 115. Si tu rentabilidad es del 12 %, tardarías 9 años y medio en triplicar tu inversión.

Fácil, ¿verdad?

Qué es el riesgo

La doctrina oficial dice que (léelo de carrerilla): el riesgo de una inversión corresponde exactamente a la volatilidad de las rentabilidades, entendida esta como la medida estadística conocida como desviación estándar (a veces la encontrarás como desviación típica) o lo que es lo mismo, la raíz cuadrada del desvío cuadrático medio con respecto a la rentabilidad media aritmética (ya puedes respirar).

Para saber cuál es el riesgo de una inversión, debes hacer algo tan “intuitivo” como aplicar la fórmula de la desviación estándar que te indico a continuación:

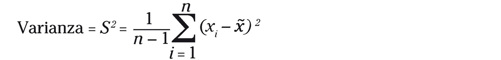
por lo que la desviación estándar será S = √S ²

En esta fórmula, X_i son cada una de las observaciones, 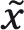es la media aritmética del conjunto de observaciones analizado y n el número total de observaciones. Pero ¿de verdad alguien se acuerda de hacer raíces cuadradas? La fórmula anterior no debe preocuparte, en productos financieros como los fondos de inversión, los planes de pensiones o los ETF (capítulos 8, 9 y 15) es un dato que te vendrá dado en la información comercial del producto y si alguna vez se te ocurre hacer de estadístico por tu cuenta, tanto en Excel como en las calculadoras financieras y científicas ofrecen el cálculo de la desviación estándar de forma automática.

¡Eooooo! ¿Sigues ahí o el libro ha salido volando por la ventana? No te asustes, esta frase podría resumirse más o menos diciendo que el riesgo de una inversión depende de lo fuertes que sean las subidas y bajadas de su rentabilidad. ¿Verdad que así se entiende mejor?

Pero vayamos por partes.

Más que ver fórmulas respecto al riesgo (la parte más técnica la encontrarás en el capítulo 16, dedicado a la gestión de carteras), lo mejor que puedes hacer es entenderlo: el riesgo es la probabilidad de que una inversión pierda valor. Si tienes claros los riesgos que asumes, no es tan importante conocer el número concreto que da la fórmula anterior.

Para acabar de entender qué es el riesgo nos ayudarán más los académicos de la Real Academia Española que la fórmula que has visto antes. Riesgo es “contingencia o proximidad de un daño” y contingencia la definen como la “posibilidad de que algo suceda o no suceda”. Y esto ocurre porque el proceso de invertir consiste en estimar el futuro, y como el futuro nadie lo conoce, nuestras inversiones siempre comportarán un determinado nivel de riesgo.

La clave es entender el riesgo, pensar y reflexionar sobre los distintos escenarios que pueden darse y cómo podrían afectar a tus inversiones.

No es “el riesgo”, son “los riesgos”

Reducir el riesgo a un único cálculo es un error. La volatilidad (la inestabilidad de la rentabilidad de un activo) es uno más de los muchos riesgos que podemos identificar en una inversión. Pero hay otros:

La pareja del año: rentabilidad y riesgo

Espero y deseo que este libro te aporte muchas cosas, pero si tuvieras que quedarte con un único concepto, solo uno y nada más que uno, por favor, que sea este. Te aseguro que habrás amortizado con creces el precio del libro:

No hay rentabilidad sin riesgo.

Las distintas clases de activos ofrecen diversas combinaciones de rentabilidad y riesgo. Veamos un ejemplo con las tres clases de activos tradicionales: liquidez, como un depósito bancario; renta fija, como un bono de una empresa; y renta variable, como una acción cotizada en bolsa. Entre esas tres podemos decir, sin temor a equivocarnos, que la acción tiene más riesgo que el bono y este, a su vez, más riesgo que un depósito bancario. En el caso del mercado español podemos ver la relación entre la rentabilidad y el riesgo del Ibex 35 y el del bono a 10 años:

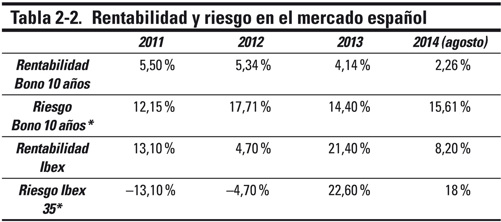
* Riesgo como rentabilidad histórica a tres meses.

Fuente: www.bde.es

Apúntatelo en tu cuaderno de inversiones, ponte un post-it o tatúatelo en el antebrazo para tenerlo siempre presente: no hay rentabilidad sin riesgo.

La forma rápida de “calcular” la fórmula de la desviación estándar (que es la medida del riesgo, como te decía en páginas anteriores) sin calculadora es la siguiente: si una inversión promete una rentabilidad del 10 y otra del 5 %, te puedo asegurar que la del diez tiene más riesgo que la del cinco. A mayor rentabilidad, más riesgo.

Repite en voz alta (en serio): no hay rentabilidad sin riesgo, no hay rentabilidad sin riesgo, no hay... ¿lo estás diciendo en voz alta? No hay rentabilidad sin riesgo, no hay...

Pero sin riesgo tampoco hay rentabilidad

Amigo, pensabas que esto era fácil y que se trata de invertir en activos de bajo riesgo, ¿verdad? Pero la clave para invertir bien y cumplir tus objetivos como inversor es hallar la combinación de rentabilidad y riesgo adecuada para ti. Y encontrar el equilibrio no es fácil.

En el apartado anterior te he dicho que “no hay rentabilidad sin riesgo” y te he pedido que lo memorices. Pero para encontrar la combinación adecuada de rentabilidad y riesgo también debes recordar que sin riesgo no hay rentabilidad.

Nos viene muy bien la tabla 2-2, que compara el Ibex 35 y el bono español a 10 años. Es una serie muy corta pero muestra el concepto que estamos tratando. En 2012, los inversores de la bolsa española asumieron un riesgo (volatilidad) muy elevado, del 31 %, para acabar el año con pérdidas de casi un 5 %. Pero al año siguiente esa inversión de riesgo proporcionó más de un 21 % anual, una rentabilidad magnífica. Por el contrario, los inversores en bonos no sufrieron la volatilidad de los inversores en bolsa, y ambos años obtuvieron beneficios. Haciendo el cálculo de la rentabilidad de varios periodos que ya conoces, los inversores en bolsa española obtuvieron una rentabilidad acumulada en ese periodo (2012-2013) del 15,69 %, mientras que los inversores en bonos ganaron un 9,70 %. El que quiso ganar más, tuvo que arriesgar más.

El “trabajo” de un inversor es asumir riesgos inteligentes y obtener un beneficio por ello.

Una muestra de que la volatilidad es buena y necesaria para que tu cartera de inversión alcance sus objetivos nos la ofrecen los gestores profesionales. En una entrevista que publicó la revista profesional Funds People en febrero de 2011, a uno de los mejores gestores de renta variable de España, Francisco García Paramés, este dijo: “Yo pongo una velita a mis santos favoritos para que aumente la volatilidad, cuanta más volatilidad a corto plazo, más rentabilidad a largo plazo. Lo decía Warren Buffet: prefiero un 10 % anual volátil que un 3 % sin volatilidad”. Y los gestores de Metagestión, en un comunicado a sus clientes publicado en la comunidad de profesionales de la inversión Funds People, en febrero de 2012, afirmaban que “la volatilidad tiene que ser nuestra aliada, no nuestra enemiga”.

Cómo calcular el riesgo de tus inversiones

Ahora sí. Ya podemos entrar en cálculos para ver plasmado en números lo que espero que conceptualmente tengas claro. Me refiero al nivel de riesgos de tu cartera de inversión. Algunos conceptos que siempre debes tener presentes a la hora de invertir son:

Me voy a detener un momento en el último concepto: control de riesgo frente a búsqueda de rentabilidad.

Supongamos que tienes una cartera que vale 100 y has tenido tan mala suerte que cae un 50 %. Te tranquilizas y quizá piensas: “Bueno, como tengo tiempo por delante, se trata de ser paciente porque si ha caído un 50 puede subir otro 50”. ¡Error! (Algo que ya sabías por el cálculo de la rentabilidad media geométrica que hemos visto antes.) Has caído en una trampa de percepción en la que absolutamente todos los inversores hemos caído en algún momento: la asimetría entre beneficios y pérdidas. Es muy sencillo: si inviertes 100 euros y la rentabilidad cae el 10 %, te quedas con 90 euros. Si más tarde la rentabilidad sube un 10 %, esos 90 euros se convertirán en 99, algo menos que los 100 que invertiste al principio. Así pues, si te has quedado en 90 y quieres volver a tus 100 iniciales, la rentabilidad tendrá que ser del 11,11 %. Observa la tabla 2-3:

 

La asimetría entre beneficios y pérdidas nos enseña que si tu inversión cae un 50 % no precisas otro 50 % para recuperarte: necesitarás un 100 % y obtener ese tipo de rentabilidades no es tarea fácil.

Hay dos clases de inversiones: la conservadora y la mala

El título de este apartado es contextual. No estoy diciendo que todo el mundo deba ser conservador en extremo. Dependiendo del contexto de cada inversor y de sus circunstancias personales (como el horizonte temporal, el objetivo buscado y el nivel de riesgo asumible) debe escogerse la inversión más conservadora posible y no buscar atajos que incrementen innecesariamente el nivel de riesgo. Si, después de valorar todos los factores, una cartera de inversión debe tener un máximo de un 50 % de bolsa, según la visión conservadora de ese perfil, lo que no debe tener es un 80 % porque “creo que este año va a subir” o porqué el gurú de turno ha dicho que es el año de la bolsa.

Ante todo, control del riesgo.

Como has visto, hay muchos tipos de riesgo, pero la forma de materializar el nivel de riesgo de una inversión es valorar lo volátiles que son las rentabilidades que proporciona a lo largo del tiempo. Este es el concepto clave que se maneja en la gestión de carteras. Cuanto más varía el precio de un activo a lo largo del tiempo, mayor es la incertidumbre de su valor futuro, mayor es su volatilidad y, por tanto, también lo será su riesgo. Para calcular esas variaciones se aplica una medida de dispersión estadística como la desviación estándar sobre las rentabilidades que proporciona dicho activo. Ahora, si quieres, puedes volver al principio del capítulo y aprenderte la fórmula de memoria (aunque no te lo recomiendo). En la tabla 2-4 te presento un ejemplo de aplicación del concepto de desviación estándar.

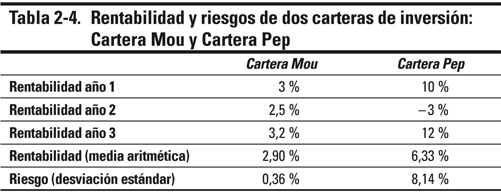
La desviación estándar mide la dispersión de las rentabilidades respecto de su valor medio y, a mayor dispersión, mayor riesgo. Puedes visualizarlo como la distancia media entre cada rentabilidad y su media. Imagínate la media como un camino: cuanto más se alejan las rentabilidades del camino, mayor es la dispersión, la incertidumbre sobre los resultados futuros y, por lo tanto, también el riesgo.

Según la tabla 2-4, la cartera Mou (los nombres los he tomado de una entretenida competición entre dos carteras de fondos que publiqué en mi blog durante un año entero) es más conservadora, así que asume menos riesgo. Un 0,36 % es nada, pero a cambio renuncias a rentabilidad potencial. Por otro lado tienes la cartera Pep con un riesgo veintidós veces superior al riesgo Mou, pero ofrece una mayor rentabilidad potencial.

Estas dos carteras muestran la gran verdad de la inversión, que no me cansaré de repetir, aun a riesgo de hacerme pesado: no hay rentabilidad sin riesgo.

Time is money (pero no al revés)

Si las fórmulas te agobian, no sigas leyendo. Mi objetivo con este capítulo es aclarar la relación entre rentabilidad y riesgo, y eso seguro que ya lo sabes.

Pero si no sigues leyendo te perderás de lo bueno lo mejor: cómo transformar euros del futuro en euros de hoy y viceversa, euros de hoy en euros del futuro. Te perderás la magia de las finanzas. Y si no sigues leyendo tampoco sabrás cuál ha sido el fichaje más caro de la historia del fútbol. Si fuera tú no me lo pensaba dos veces y seguiría leyendo. Ni que sea por el fútbol.

Valor del Dinero en el Tiempo (VDT)

¿Quieres tener hoy 100 euros en tu bolsillo o prefieres tenerlos dentro de un año? (Si tu respuesta es “dentro de un año” ¡háztelo mirar!)

Un euro recibido hoy tiene más valor que un euro recibido en el futuro (en el capítulo 1 encontrarás un ejemplo muy ilustrativo sobre una casa en Boadilla). ¿Por qué? Pues porque:

1.   A mayor plazo, mayor incertidumbre. Si le dejas 100 euros a tu amigo Juan hasta el próximo sábado es una cosa; si te dice que te los devolverá dentro de 10 años... ¡Quién sabe lo que habrá ocurrido en ese tiempo! Cambia a tu amigo Juan por el producto financiero que quieras. Un depósito a plazo fijo a 3 meses tiene menos incertidumbre que el mismo depósito en el mismo banco a cinco años. Es el mismo producto financiero y del mismo banco, pero amigo, recuperar el dinero a los tres meses no es lo mismo que esperar cinco años.

2.   La inflación, que, como hemos visto en el capítulo 1, es nuestro enemigo natural y recorta nuestra capacidad de compra.

3.   El euro que tenemos hoy podemos reinvertirlo y generar beneficios adicionales, teniendo más de un euro en el futuro.

Una inversión a largo plazo debe ofrecernos una promesa de rentabilidad mayor que una inversión de riesgo similar a corto plazo.

Valor presente y valor futuro

Ambos conceptos derivan del Valor del Dinero en el Tiempo (VDT) del que te acabo de hablar. El valor futuro de una inversión que se realiza hoy depende del tipo de interés que te den y del plazo transcurrido. Se expresa así:

VF = VP × (1 + I)^T

La fórmula puede parecer complicada pero deja de serlo si entiendes su lógica:

Para facilitarlo un poco, te pondré un ejemplo. ¿Cuál es el valor futuro de una inversión de 100 euros a tres años en la que obtengo un 4 % anual? Pues algo como esto:

VF = 100 × (1 + 0,04)³ = 112,49

Con el valor futuro nos movemos de hoy hacia delante. En términos financieros, esto se llama capitalizar. Transformo euros de hoy en euros futuros.

Pero también puedes hacer lo contrario, traer euros del futuro a euros de hoy o, como dicen los financieros, descontar. Sé que necesito que, dentro de tres años, mi plan de inversiones sea de 112,49 euros y tengo una inversión que promete un 4 % a tres años. De la formulita anterior podemos deducir lo siguiente:

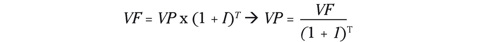
En nuestro ejemplo, y para calcular cuánto necesito invertir hoy para obtener 112,49 euros dentro de tres años, el valor presente será igual a

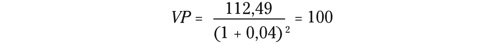
Resumiendo, puedes hacer simulaciones sobre tus planes de inversión de forma muy fácil con estos dos conceptos:

Tenlos presentes porque son básicos en el arte de la inversión.

Una herramienta de cálculo

Los conceptos anteriores me vienen muy bien para presentarte una herramienta de cálculo imprescindible en el mundo financiero como es el modelo de descuento de flujos de caja o DCF, discounted cash flow del que derivan el valor presente o actual, y la Tasa Interna de Rentabilidad (TIR), la piedra angular de la inversión. Este tipo de cálculo es fundamental tanto en renta fija (bonos) como en renta variable (acciones), ya que nos permite valorar ambos tipos de activos. No dejes que los nombres compuestos te amedranten, pues desde un punto de vista práctico no son más que operaciones aritméticas básicas que se pueden sacar con facilidad en un Excel y en las calculadoras financieras.

La fórmula general del descuento de flujos nos indica que el valor de un activo viene dado por dos factores:

Cuando 100 euros no valen 100 euros...

Si nos complicamos la vida con esto es por la realidad que muestra el valor del dinero en el tiempo. No podemos comparar euros percibidos en distintos momentos, ya que tienen diferente capacidad de compra (recuerda el efecto de la inflación que te explicaba en el capítulo 1). No podemos sumar euros a recibir dentro de un año con euros a recibir dentro de diez sin homogeneizarlos... Y ahí entra el cálculo del valor presente que te he explicado antes.

Fíjate en la siguiente fórmula:

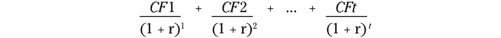
Para acabar de entender la fórmula, ten en cuenta que CF es aquí el flujo monetario (cash flow) que produce la inversión en cada periodo, mientras que r es la tasa de descuento (la rentabilidad, el tipo de interés que le pedimos a esa inversión) y t es el tiempo.

Imagina que una inversión nos promete un pago el primer año (flujo de caja o cash flosw) de 150 euros y el segundo año de 500, con una tasa de descuento del 6 % (te recuerdo que los tipos de interés se indican en tanto por uno, en este caso, 0,06).

El ingreso total que nos proporciona el activo es de 650 euros (150 y 500) pero, aplicando la tasa de descuento que, para este activo, consideramos del 6 %, el valor presente, el valor de ese activo hoy es de 586,51 euros. Matemáticamente, la conclusión es que nos da igual recibir hoy 586,51 euros que 150 dentro de un año más 500 euros dentro de dos. Como te he dicho en el apartado anterior, el paso del tiempo afecta al valor del dinero.

Y sigamos con las fórmulas, porque de la del valor actual se deduce otra básica en la valoración de inversiones que es el Valor Actual Neto (VAN). El único elemento nuevo que incorpora es la inversión realizada o CFo:

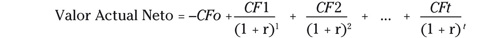
El CFo o cash flow cero es la inversión inicial y va con signo negativo, pues no es algo que ganes, sino el punto de partida. Supón que, en el caso anterior, la inversión ha sido de 500 euros.

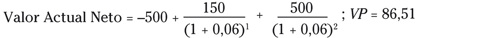
La regla general es que si el VAN es mayor que cero, la inversión nos aporta valor y es positiva para nuestro patrimonio. Si es menor que cero, no hay que invertir.

Una vieja conocida, la TIR

Y por fin llegamos a la llave inglesa de las finanzas, a la Tasa Interna de Rentabilidad o TIR. Acabamos de explicar el VAN y has visto que debemos aplicar una tasa de descuento (rentabilidad libre de riesgo + prima de riesgo). Pues bien, la Tasa Interna de Rentabilidad es la tasa de descuento que hace que el Valor Actual Neto de la inversión sea cero (VAN = 0). La fórmula es la misma que usamos para calcular el VAN pero, para hacerlo gráfico, vamos a cambiar la tasa de descuento r por la TIR. ¡No te líes! Es lo mismo que veíamos más arriba, simplemente es para que lo veas de forma más clara.

La regla general es que si la TIR es mayor que la tasa de descuento, la inversión nos interesa y, si es inferior, no. Si nos hubiese salido una TIR del 2 % cuando nuestra exigencia para esta inversión es de un mínimo de un 6 % no deberíamos invertir, mientras que un 16,12 % es un inversión que, si analizamos la TIR, nos conviene.

Otro uso estupendo que tiene la TIR es calcular la rentabilidad de una inversión activa.

Imagínate que compras acciones de una compañía por 500 euros. Como va bien y te gusta, inviertes 3.000 más, luego vendes una parte por valor de 1.500 euros y al final, viendo que ya ha subido mucho, decides liquidar tu inversión y sacas 4.500. ¿Qué rentabilidad te ha dado? Con la TIR es muy fácil plantear el cálculo:

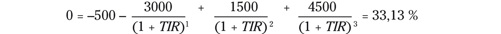
No te quiero engañar. Así como el cálculo del VAN no es complicado, sacar la TIR es algo más complejo. Pero recuerda, un Excel o la calculadora financiera te serán de gran ayuda.

La TIR es básica para determinar rentabilidades, especialmente en el ámbito de la renta fija (bonos), aunque es aplicable a cualquier tipo de inversión y su uso es continuo en el ámbito profesional.

Es posible que tanto en calculadoras financieras como en algún texto te encuentres con la expresión NPV, Net Present Value, que es nuestra VAN, y también con IRR, Internal Rate of Return, nuestra TIR.