ENTRELAZAMIENTO TRIPLE

En un capítulo anterior, dejamos a Michael Horne disfrutando del éxito de su trabajo con Abner Shimony, John Clauser y Richard Holt (CHSH) y de la prueba real del entrelazamiento mediante un test experimental de la desigualdad de Bell, con resultados a favor de la mecánica cuántica, llevado a cabo por Clauser y Freedman. El éxito de CHSH y sus demostraciones experimentales consiguientes recibió amplia atención en la literatura física y fue una novedad científica. Hubo artículos que informaban sobre los nuevos descubrimientos y hubo asimismo nuevos experimentos y un renovado entusiasmo hacia los fundamentos del extraño mundo del cuanto.

Poco después, Clauser, Horne y Shimony entraron en contacto con el hombre que lo había empezado todo: John Bell. Se entabló una comunicación frecuente entre los cuatro, que en parte apareció como artículos científicos, con la intención de responder cuestiones y discutir ideas propuestas por uno u otro lado. Esta fructífera comunicación dio como resultado una demostración del teorema de Bell con menos hipótesis restrictivas, y también mejoró nuestra comprensión del asombroso fenómeno del entrelazamiento.

En 1975, Mike Horne entró en un grupo de investigación dirigido por Cliff Shull del MIT, que realizaba experimentos con neutrones producidos en el reactor nuclear del MIT en Cambridge (Massachusetts). Mike pasó diez años en el reactor, realizando experimentos de interferencia con neutrones. También conoció allí a dos físicos que cambiarían el curso de su carrera, y cuyo trabajo en colaboración con él daría lugar a un salto gigantesco en nuestra comprensión del entrelazamiento. Los dos científicos eran Daniel Greenberger y Anton Zeilinger. Los tres escribirían un artículo fundamental en el que probarían que tres partículas podían estar correlacionadas, y pasarían años estudiando las propiedades de tales tríos entrelazados. Cuando, años después, les pregunté si ellos tres estaban de alguna manera «entrelazados», como los tríos de partículas que habían estudiado, Anton Zeilinger respondió rápidamente: «Sí, estábamos tan compenetrados que cuando uno abría la boca para decir algo, los otros acababan la frase por él…». La trayectoria de Michael Horne, desde los estudios de interferencia de dos partículas a la investigación sobre interferencias de una simple partícula, tenía detrás una buena razón. Después de hacer el trabajo CHSH que ayudaba a establecer el entrelazamiento como un principio clave en los fundamentos de la mecánica cuántica, Mike decidió estudiar otros problemas relacionados con esos fundamentos. Conocía muy bien la historia del desarrollo de las ideas en teoría cuántica a medida que esta disciplina evolucionaba. Sabía que cuando Young realizó su famoso experimento con la luz en los primeros años de 1800 y descubrió el patrón de interferencias que todavía nos intriga hoy, la luz (y otras radiaciones electromagnéticas) era la única «onda» microscópica conocida. Después, en 1905, Einstein propuso el fotón como una explicación del efecto fotoeléctrico, mostrando que la luz no era sólo una onda, sino también una corriente de partículas. Sabía asimismo que en 1924 De Broglie «conjeturó que incluso las partículas son ondas», en palabras de Mike, pero que «nadie por entonces era capaz de realizar un experimento del tipo doble rendija con electrones, aunque una confirmación directa de las ondas de De Broglie llegó enseguida de la difracción de electrones por sólidos cristalinos». Un cuarto de siglo después, en la década de 1950, el físico alemán Möellenstedt y sus colaboradores llevaron a cabo el experimento. Probaron que esas partículas, los electrones, muestran la misma naturaleza ondulatoria expuesta por un patrón de interferencia en una pantalla tras emerger del viejo dispositivo de doble rendija de Young.

Después, a mediados de los años setenta, primero Helmut Rauch en Viena y posteriormente Sam Werner en Missouri realizaron de forma independiente lo que esencialmente era un experimento de doble rendija con neutrones. Estos objetos cuánticos con masa muestran el mismo patrón de interferencia que asociamos con ondas en el dispositivo experimental de la doble rendija. Ambos grupos experimentales, de Viena y Missouri, usaron neutrones térmicos: neutrones producidos en reacciones que tenían lugar en un reactor nuclear. Esos neutrones viajaban a velocidades bajas (comparadas con la de la luz), de unos mil metros por segundo, y por tanto, según la fórmula de De Broglie, su longitud de onda asociada era de unos pocos amstrongs. Estos muy atrevidos experimentos eran ahora posibles por las nuevas tecnologías de superconductores, que permitían disponer de grandes y perfectos cristales de silicio. Los científicos usaban cristales de silicio de un tamaño del orden del decímetro para construir interferómetros para los neutrones térmicos provenientes del reactor. Como los neutrones interactuaban con la red cristalina, primero el haz de neutrones se dividió mediante difracción en una porción del cristal y después las otras porciones se usaron para redirigir y recombinar los haces a fin de producir finalmente el patrón de interferencia.

Mike estaba muy interesado en esos experimentos, que se llebavan a cabo por entonces. Sabía que Cliff Shull, uno de los pioneros del trabajo con neutrones en los años cuarenta (que recibiría el premio Nobel en 1994), tenía un laboratorio en el reactor del MIT y realizaba allí experimentos con neutrones térmicos. Mike tenía ya una plaza para enseñar física en el Stonehill College, pero allí no había un reactor ni ningún físico conocido que realizara experimentos interesantes. De manera que, un día de 1975, Mike se dirigió al laboratorio de Cliff Shull en el MIT para presentarse. Mencionó a Shull su trabajo sobre el entrelazamiento con Shimony y Clauser y le comentó su interés en los experimentos de interferometría de neutrones. Después le preguntó si podía participar.

«Ocupa esa mesa de la derecha», fue la respuesta de Shull, señalando una mesa a la derecha del laboratorio. Desde ese día, durante diez años, de 1975 a 1985, todos los veranos, todas las vacaciones de Navidad y todos los martes (el día que no daba clase) Mike Horne estaba en el laboratorio de Shull en el MIT trabajando en difracción de neutrones. Encontró particularmente atractivos dos experimentos con neutrones que se habían realizado en Viena y Missouri. El grupo de Shull realizaría otros muchos experimentos en el MIT.

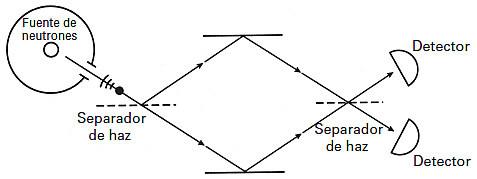
El experimento realizado por Sam Werner y colaboradores en la Universidad de Missouri en 1975 demostraba directamente la influencia de la gravedad sobre los neutrones en un experimento de interferencia tipo doble rendija, lo que no había sido demostrado anteriormente. El experimento de Missouri era elegante y conceptualmente simple, de modo que manifestaba lo esencial de tales experimentos cuánticos.

Las dos trayectorias a través del interferómetro se dispusieron en forma de diamante (de la baraja). La onda cuántica de un neutrón que penetraba en el diamante se dividía a la entrada, yendo la mitad de la onda hacia la derecha y la otra mitad hacia la izquierda. En el otro lado del diamante, cuando las dos ondas se recombinaban y salían, se encontraba un pico o un valle en la intensidad; igual que ocurría en la pantalla en el experimento clásico de Young, sólo que ahora esto sucedía en un punto y no en un continuo de puntos en la pantalla. Los científicos registraban si habían encontrado un pico o una depresión. Después, dándole la vuelta al cristal de silicio, giraban el diamante noventa grados, de manera que ahora estaba vertical y no horizontal. Notaron entonces que había cambiado el patrón. La razón de ello era que las dos ondas de neutrones se veían afectadas por la gravedad de manera distinta porque una de ellas estaba ahora más alta que la otra y un neutrón a un nivel más alto viajaba a menor velocidad, lo que cambiaba la longitud de onda de De Broglie a lo largo de una trayectoria respecto a la otra y, por consiguiente, desplazaba el patrón de interferencia. El experimento se muestra en la figura siguiente.

Otro experimento que efectuaron Helmut Rauch y sus colaboradores en Viena en 1975, así como un grupo de Missouri ese mismo año, fue el experimento 2π-4π con neutrones. El equipo de Rauch demostró utilizando interferometría una fascinante propiedad de los neutrones. Se usaba un campo magnético para girar 360 grados (2π) el neutrón en una trayectoria del interferómetro. Las partículas de espín entero (los llamados bosones) vuelven a su estado original cuando experimentan una rotación de ese tipo (han ido pues alrededor de un círculo completo), pero esto no sucede con el neutrón. Después de girar un ángulo de 360 grados, es decir, de dar una vuelta completa, se vio que los neutrones mostraban un cambio de signo, que podía observarse mediante la interferencia. Sólo cuando el campo magnético giraba los neutrones otra vez alrededor del círculo (esto es, una rotación de 4π), volvían éstos a su estado original.

Por esa misma época, en Boston, Abner Shimony y Mike Horne hablaban de realizar un experimento de ese tipo, con el fin de probar la propiedad 2π-4π del neutrón teóricamente conocida, sin saber que Rauch y sus estudiantes lo habían hecho ya en Viena. Mike y Abner escribieron su artículo y lo enviaron a una revista de física. Pero pronto descubrieron que el grupo de Viena había hecho lo mismo y había realizado el experimento. Uno de los estudiantes de Rauch en Viena era Anton Zeilinger.

Anton Zeilinger nació en mayo de 1945 en Ried/Innkreis, Austria. De 1963 a 1971 estudió física y matemáticas en la Universidad de Viena, obteniendo su doctorado en física por dicha universidad en 1971, con una tesis sobre despolarización de neutrones en cristales simples de disprosio, escrita bajo la supervisión del profesor H. Rauch. En 1979, realizó su trabajo de habilitación, sobre neutrones y física del estado sólido, en la Universidad Técnica de Viena. Entre 1972 y 1981, Zeilinger fue ayudante de universidad en el Instituto de Investigación Atómica de Viena, y trabajó de nuevo con Rauch.

Erice es una pintoresca ciudad medieval de Sicilia. Los físicos, no indiferentes a la belleza y a la naturaleza, se han enamorado de esa pequeña ciudad en el severo y montañoso entorno de Sicilia y han organizado allí congresos que atraen a físicos de todo el mundo. En 1976, el congreso de Erice estuvo dedicado a los fundamentos de la mecánica cuántica, incluyendo las desigualdades de Bell y el entrelazamiento. Cuando recibió el anuncio de la reunión, Rauch le dijo a Anton Zeilinger: «¿Por qué no vas a la reunión? No sabemos demasiado sobre el trabajo de Bell, pero podemos aprender y tal vez algún día realizar aquí en Viena unos experimentos tan apasionantes como se dice que son los que tratan del entrelazamiento… Ve y aprende lo que puedas». Anton, contento de obedecer, hizo la maleta y se fue a Sicilia.

Al mismo tiempo, en Boston, Abner, Mike y Frank Pipkin, de Harvard, hacían sus maletas y se disponían a partir hacia Sicilia con comunicaciones acerca de sus trabajos sobre el entrelazamiento que iban a presentar en la reunión. La de Mike Horne era sobre el trabajo que había hecho con Shimony durante años, una extensión del teorema de Bell a montajes de tipo probabilístico. En Sicilia, los físicos de Boston conocieron a Anton Zeilinger. «Enseguida hicimos buenas migas —dijo Mike Horne—. Anton estaba muy interesado e intentaba aprender de mí todo lo que pudiera sobre el teorema de Bell. Le fascinaba el entrelazamiento».

Un día, de vuelta en el laboratorio de Cliff Shull en el reactor nuclear del MIT, Cliff le preguntó a Mike con cierto desdén, mientras le mostraba la carta que tenía en la mano: «¿Conoces a una persona llamada Anton Zeilinger? Ha solicitado venir a trabajar aquí y menciona tu nombre en su carta». «¡Oh, por supuesto! ¡Fantástico! —contestó Mike—. Es un físico estupendo…, muy interesado en los fundamentos de la mecánica cuántica».

Anton Zeilinger se incorporó al equipo del MIT en el curso académico 1977-1978 como investigador posdoctoral, con la financiación de una beca Fulbright, y durante los diez años siguientes, siendo ya profesor en Viena, realizó estancias de varios meses en ese Instituto. Trabajó duramente haciendo el mismo tipo de experimento con neutrones que había hecho como estudiante de Rauch en Viena, y él y Mike Horne fueron coautores de docenas de trabajos a lo largo de esos años, junto con Cliff Shull y los estudiantes que por entonces trabajaban con ellos en el laboratorio, que cambiaban de un año para otro. Esto duró hasta la jubilación de Cliff Shull en 1987.

Mientras comían unos sándwiches, en los descansos del trabajo en el laboratorio, Anton y Mike discutían la interferencia de dos partículas, el viejo trabajo de Mike con Abner y John y Dick Holt. Pero su trabajo por entonces tenía que ver con la realización de estudios de interferencia de neutrones individuales. Las ideas del teorema de Bell para dos partículas eran por el momento solamente un apasionado hobby, un interés ajeno a su trabajo cotidiano. «Nos sentábamos allí, mientras comíamos, y yo le informaba detalladamente acerca del teorema de Bell y las teorías de variables ocultas locales y cómo son incompatibles con la mecánica cuántica —recordaba Mike Horne—, y él siempre escuchaba y quería que le siguiera explicando más y más cosas».

Daniel Greenberger nació en el Bronx (Nueva York) en 1933. Asistió al Instituto de Enseñanza Media de Ciencias del Bronx y fue compañero de clase de Myriam Sarachik (actual presidenta de la Sociedad Americana de Física y ahora compañera de Daniel en el City College of New York, CCNY) y de los premios Nobel Sheldon (Shelly) Glashow y Steven Weinberg. Estudió física en el MIT, graduándose en 1954. Fue después a la Universidad de Illinois para hacer la tesis doctoral en física de altas energías con Francis Low. Cuando Low se marchó para incorporarse al MIT, Greenberger lo siguió allí donde escribió la tesis doctoral y obtuvo el grado de doctor. En el MIT estudió física matemática, en particular métodos algebraicos para explorar las simetrías, tan populares ahora en física teórica. A principios de los años sesenta, se unió al grupo de Jeffrey Chew en la Universidad de California en Berkeley, y disfrutó de una beca posdoctoral para trabajar en física de altas energías. Estando en Berkeley, se enteró de que el CCNY había abierto una escuela de graduados con un programa en física, de manera que se marchó allí en 1963; desde entonces, es profesor en ese centro.

Danny se ha sentido siempre fascinado por la teoría cuántica. Él sostiene que la mecánica cuántica no es simplemente una teoría que converge en la física clásica cuando aumenta el tamaño de los objetos en cuestión, sino que, más bien, es una teoría independiente con una riqueza inmensa que no se nos muestra de forma inmediata. Le parece que la mecánica cuántica se asemeja a las islas Hawai. Cuando nos acercamos a las islas sólo vemos la parte por encima de la superficie del mar: las costas y las montañas. Pero por debajo de la superficie del mar existe una inmensa dimensión oculta que se extiende hasta el fondo del océano Pacífico. Y para demostrar que la mecánica cuántica no es una extensión de la física clásica sino que posee esta dimensión oculta, pone como ejemplo la rotación de los objetos físicos. El momento angular, nos recuerda, es un elemento de la física clásica y tiene su análogo en la mecánica cuántica, pero el espín es algo peculiar de los objetos que habitan el mundo cuántico y no tiene análogo en la física clásica.

Greenberger estaba interesado en la relación entre la teoría de la relatividad y la mecánica cuántica. En particular, le interesaba verificar si el importante principio einsteniano de la equivalencia de la masa inercial y la masa gravitatoria era cierto desde el punto de vista cuántico. Se dio cuenta de que para verificarlo necesitaba estudiar objetos cuánticos afectados también por la gravedad. Conocía uno de esos objetos: el neutrón. Los físicos habían buscado desde siempre la conexión entre la relatividad general, que es la teoría moderna de la gravedad, y el mundo cuántico. Los neutrones son objetos cuánticos porque son pequeños, pero también les afecta la gravedad. De manera que la conexión entre ambas teorías podría tal vez encontrarse mediante el estudio de los neutrones.

Greenberger se puso en contacto con los científicos que investigaban sobre neutrones en el reactor del Brookhaven National Laboratory en Long Island, pero le dijeron que ellos no realizaban estudios de interferencia con neutrones. Descubrió, sin embargo, que Cliff Shull hacía esa investigación en el MIT, y en 1970 viajó a Cambridge (Massachusetts) para entrar en contacto con él. Cinco años después, leyó un artículo de Colella, Overhauser y Werner sobre el efecto Aharonov-Bohm, y se puso en contacto con Overhauser e intercambió con él ideas acerca de tal efecto. Danny se dio cuenta de que había algún aspecto que precisaba ser investigado en detalle. Más tarde publicó un artículo sobre dicho efecto en Reviews of Modern Physics. En 1978 hubo un congreso sobre estos temas en el gran reactor nuclear de Grenoble, Francia. Overhauser, que no podía asistir al congreso, le pidió a Greenberger que fuera en su lugar.

En Grenoble, Danny conoció a Anton Zeilinger, quien por entonces trabajaba a tiempo parcial en el reactor del Instituto Laue-Langevin como investigador invitado. Y también conoció a Mike Horne, que asistía asimismo al congreso. Como los tres se interesaban por el mismo tema, se estableció una ligazón entre ellos. «Ese congreso cambió mi vida —recordaba Zeilinger—. Nosotros tres hicimos realmente buenas migas». Desde Grenoble Anton regresó a Austria para continuar allí su trabajo de investigación, y al ir de nuevo al MIT le encantó ver que Danny Greenberger se había incorporado al equipo del Instituto para una breve estancia. Pero la visita se repetiría numerosas veces durante muchos años —hasta el retiro de Cliff Shull en 1987—, posibilitando que los tres científicos trabajasen en común. Incluso después de dicho retiro, una ayuda concedida por la NSF (National Science Foundation) junto con Herbert Bernstein del Hampshire College les permitió continuar sus investigaciones.

Anton realizó después estancias en el MIT de varios meses, alguna incluso de un año; Danny fue allí para visitas cortas de algunas semanas cada una. La excepción fue la estancia larga de Danny en 1980, cuando disfrutó de un año sabático. Los tres físicos pronto se convirtieron en un grupo fuertemente unido dentro de la más extensa comunidad de científicos que trabajaban en el reactor del MIT, y pasaban además muchas horas hablando fuera del laboratorio acerca del entrelazamiento, un tema que revestía gran interés para los tres. Aunque en el laboratorio trabajaban únicamente en interferencias de una partícula (neutrón), muchas de sus discusiones fuera del laboratorio se centraban en interferencias de dos partículas y el teorema mágico de Bell.

El entrelazamiento entre los tres físicos fue completo. Danny y Mike se dieron cuenta simultáneamente de algunos problemas teóricos en relación con el famoso efecto Bohm-Aharonov de los años cincuenta y trabajaron independientemente en este tema. Danny Greenberger publicó sus hallazgos en una revista. Anton y Danny propondrían ideas estrechamente relacionadas sobre física, y lo mismo sucedería entre Mike y Anton, quienes durante diez años escribirían artículos en colaboración sobre su investigación en interferometría de una partícula basados en su trabajo en el laboratorio de Shull. En 1985, Mike y Anton publicaron entre los dos un artículo sobre entrelazamiento que proponía un experimento para probar que el fenómeno existe también para las posiciones (además de para el espín o la polarización) de las dos partículas, y que el teorema de Bell se aplicaría asimismo en este caso.

Un día de 1985, Anton y Mike vieron un anuncio de un congreso en Finlandia organizado para celebrar el quincuagésimo aniversario del artículo de Einstein, Podolsky y Rosen (EPR) y de la revolución en la ciencia por él engendrada, y decidieron que sería formidable asistir. Pero necesitaban poder presentar en el congreso una comunicación sobre interferencia de dos partículas, puesto que su investigación sobre una partícula no parecía adecuada a tal fin. Unos días más tarde tenían un diseño de «doble diamante» para un nuevo tipo de experimento de tests de las desigualdades de Bell, lo cual constituyó su contribución al congreso. La idea era producir fotones entrelazados y después realizar un experimento de interferencia con estos fotones, usando el doble diamante. Su diseño se muestra a continuación.

En este diseño experimental, una fuente especial emite simultáneamente dos partículas, A y B, que viajan en direcciones opuestas. Así pues, las partículas del par pueden pasar a través de los agujeros a y b o de los agujeros a’ y b’. Supongamos que la partícula B es capturada en uno de los detectores que «vigilan» los agujeros b y b’. Si la partícula B pasa por b, sabemos que la partícula A atraviesa el agujero a. Igualmente, si la partícula B pasa por b’, la partícula A lo hará por a’. Entonces, por cada cien partículas producidas por esta fuente, cada uno de los detectores de la derecha registrará cincuenta partículas «A»; es decir, no hay interferencias simples (de una sola partícula) en este caso, porque el acceso a la partícula B puede revelar qué camino toma la partícula A. De hecho, ni siquiera es necesario poner detectores junto a los agujeros b y b’; el simple hecho de que pudiéramos determinar el agujero por el que pasa la partícula B basta para destruir las interferencias (tipo una partícula) para la partícula A.

Así pues, imaginemos que se quitan los detectores junto a b y b’ y que los dos detectores de la derecha («A») y los dos de la izquierda («B») se controlan mientras la fuente emite cien pares. La mecánica cuántica predice que cada detector contará cincuenta partículas; es decir, no hay interferencia de una partícula para A ni para B porque podríamos determinar la ruta de cada partícula «atrapando» la otra cerca de la fuente. Pero la mecánica cuántica sí predice una asombrosa correlación entre las cuentas registradas. Si B «cae» en el detector inferior izquierdo, entonces A caerá ciertamente en el superior derecho; y si B se detecta en el superior izquierdo, A se detectará en el inferior derecho. Los detectores superior derecho y superior izquierdo nunca se disparan al unísono, como tampoco lo hacen el inferior derecho y el inferior izquierdo. Sin embargo, si movemos uno de los separadores de haz una distancia apropiada hacia uno u otro lado, las correlaciones cambiarán completamente. Los dos detectores de arriba (y de abajo) se disparan ahora en coincidencia, mientras que los detectores en diagonal nunca lo hacen (en coincidencia). No obstante, la tasa de cuentas de cada uno de los detectores sigue siendo cincuenta, con independencia de las posiciones de los separadores de haz. Este comportamiento se explica en mecánica cuántica diciendo que cada par de partículas se emite a través de ambos agujeros a y b, y a través de ambos agujeros a’ y b’. Este misterioso estado cuántico es un ejemplo de entrelazamiento de dos partículas.^[17.1]

Un día, mientras estaban sentados en la cocina de Mike Horne, Danny Greenberger le preguntó: «¿Qué crees que pasaría en el caso de entrelazamiento de tres partículas?». En primer lugar, la pregunta era: ¿cuáles son los detalles del entrelazamiento de tres partículas? Pero también era: ¿cómo podrían las hipótesis de EPR tratar el caso de tres partículas? ¿Existiría alguna dificultad especial al tratar de dar cuenta de manera realista y local del entrelazamiento, o el conflicto entre la mecánica cuántica y la localidad einsteniana sería esencialmente el mismo que en el caso de dos partículas? Danny se convenció de que ésa era una línea de investigación muy apropiada para desarrollar durante su año sabático, a punto de empezar. Y, previendo posibles experimentos, recordó que en el montaje de Wu-Shaknov de emisión del positronio, cuando las dos partículas (electrón y positrón) se aniquilaban mutuamente, se emitían normalmente dos fotones, pero, según las leyes de la probabilidad de la mecánica cuántica, con cierta frecuencia tendrían que emitirse tres fotones. Éste era un posible montaje experimental que considerar durante el proyecto de investigación. Mike Horne meditó sobre la pregunta de Danny y contestó: «Creo que sería un buen proyecto para desarrollar». Greenberger se fue a casa y reflexionó sobre el problema. Unos meses después volvió a ver a Mike y le dijo: «Estoy obteniendo grandes resultados sobre el entrelazamiento de tres partículas. Tengo desigualdades que surgen de todas partes. Creo que el entrelazamiento de tres partículas puede ser un desafío a EPR mayor que el de dos partículas». Mike se interesó por ello, pero también sabía que el teorema de Bell y los experimentos habían probado que EPR estaban equivocados y, por tanto, no existía una necesidad acuciante de otra prueba. No obstante, estaba lo bastante interesado en la física del entrelazamiento de tres partículas como para discutir la situación con Danny, así que le animó a continuar.

En 1986, cuando Anton estaba de regreso en Viena trabajando con Rauch, Danny obtuvo una beca Fulbright, lo que le permitió viajar a Europa en su año sabático. Decidió aprovechar la oportunidad para encontrarse con Anton en Austria y trabajar con él. Mientras viajaba a través del Atlántico tenía en la cabeza permanentemente el asunto del entrelazamiento de tres partículas. Cuando llegó a Viena, ya tenía algunas buenas ideas. Sentía que se hallaba cerca del teorema de Bell sin desigualdades. En Viena, Anton y Danny compartieron despacho, y Danny siempre le mostraba a Anton el desarrollo de sus resultados teóricos, que los dos discutían extensamente. Por fin, Danny Greenberger tuvo frente a sí una situación en la que una correlación perfecta entre tres partículas bastaba para probar el teorema de Bell. Ya no había necesidad de trabajar con una correlación parcial entre dos fotones, como habían hecho experimentalmente Clauser y Freedman, Aspect y otros. Ahí tenía una prueba tremendamente poderosa —y no obstante, conceptualmente más simple— del teorema de Bell. «Publiquémoslo», dijo Danny, y Anton repuso que Mike y él habían hecho cierto trabajo relacionado con ello que debería incluirse en el mismo artículo. Ambos hablaron por teléfono con Mike Horne, que estaba en Boston, y decidieron poner a punto un artículo sobre el tema.

En 1988, mientras ojeaba un volumen de la revista Physical Review Letters en el laboratorio de Shull, Mike vio un artículo de Leonard Mandel. El artículo contenía un diseño experimental casi idéntico al que habían propuesto Anton y él en su colaboración para el congreso de Finlandia. La única diferencia es que el diseño de interferencia de dos partículas de Mandel era un «diamante» plegado, no extendido como en la figura de Horne-Zeilinger. Pero Mandel, que no había visto las actas del congreso de Finlandia, había llevado a cabo el experimento; utilizó el método de conversión a la baja para producir fotones entrelazados. De manera que la interferencia de dos partículas no sólo era un experimento ideal, sino también algo real. Y, además, los experimentos tipo Bell podían ahora hacerse con entrelazamiento del haz y sin espín o polarización.

Como Anton y Mike habían presentado sólo en congresos su propuesta de experimentos de interferencia de dos partículas y desigualdades de Bell sin polarización, y puesto que su concepción del entrelazamiento como base de la interferencia era diferente y más simple que la de Mandel, decidieron publicar un artículo en Physical Review Letters presentando sus resultados. Abner colaboró con ellos en la redacción. Como el artículo era esencialmente un comentario sobre el importante artículo de Mandel, éste fue designado árbitro (referee) para su publicación. Siguió entonces un largo período de actividad y cooperación, en el que se prosiguió el trabajo de interferometría de dos partículas por parte del equipo de Boston, Mandel en Rochester, Shih en Maryland y otros.

Tras haber decidido en 1986 trabajar juntos en un artículo sobre entrelazamiento de tres partículas, Anton, Mike y Danny dejaron de alguna manera en suspenso el proyecto de escribir y continuaron su trabajo habitual. Danny Greenberger dejó Viena y viajó por Europa. Cuando acabó su año sabático, volvió a Nueva York y a su trabajo regular de enseñanza. Durante los dos años siguientes, no se hizo nada con los emocionantes nuevos resultados acerca del entrelazamiento de tres partículas. Entonces, en 1988, a Danny le concedieron una beca Alexander von Humboldt para trabajar como investigador en el Instituto Max Planck de Garching, Alemania, donde pasaría ocho meses como investigador visitante. Cuando estaba allí, llamó a Anton a Viena. «Ahora tengo tiempo para escribir —le dijo—. Tengo ya setenta páginas, y apenas he comenzado». Pero la redacción formal no progresaba. Danny viajó por Europa, dando charlas acerca de su trabajo con Anton y Mike sobre las propiedades de las tres partículas entrelazadas y cómo estaban relacionadas con el teorema de Bell y con el trabajo de EPR. Al final del verano de 1988, Danny Greenberger fue al congreso de ese año en Erice, Sicilia, y dio una charla sobre el entrelazamiento de tres partículas. David Mermin, de la Universidad de Cornell —otro físico cuántico— estaba entre el público. Según Danny, su sensación fue que el trabajo no atraía realmente la atención de Mermin.

Pero cuando regresó a Nueva York, Danny empezó a recibir artículos de diversos grupos de físicos que hacían referencia a su propio trabajo con Mike y Anton. Uno de esos grupos estaba dirigido por Michael Redhead, de la Universidad de Cambridge. El grupo de Redhead aseguraba haber mejorado el trabajo de Greenberger-Horne-Zeilinger sobre el entrelazamiento de tres partículas, que Danny había presentado en Erice y otros lugares de Europa. Danny llamó a Anton y a Mike. «Debemos hacer algo enseguida —les dijo—. La gente cita nuestro trabajo sin haberse publicado».

En 1988, Danny presentó una comunicación en un congreso de la Universidad George Mason (EE.UU.), que fue publicada en las actas correspondientes. Mientras tanto, David Mermin recibió el artículo de Redhead, que citaba el trabajo de Greenberger, Horne y Zeilinger, y escribió un artículo para su columna «Reference Frame» (Sistema de Referencia) en Physics Today titulado «¿Qué pasa con estos elementos de realidad?». Physics Today es el boletín de la Sociedad Americana de Física y, por tanto, el artículo tuvo una gran distribución. La comunidad de físicos se enteró perfectamente de los nuevos descubrimientos, refiriéndose a ellos como el «entrelazamiento GHZ», a pesar incluso de que el artículo anticipado de Greenberger, Horne y Zeilinger todavía no se había publicado (en muchas ramas de la ciencia, un artículo incluido en las actas de un congreso cuenta menos que un artículo publicado en una revista con referee). De hecho, dos de los autores ni siquiera sabían que se había presentado en un congreso y publicado en sus actas una comunicación que llevaba sus nombres, porque Danny había olvidado mencionárselo.

Un día Abner le preguntó a Mike: «¿Qué es eso que has probado con Danny y Anton?». «¿A qué te refieres?», le preguntó a su vez Mike Horne. Abner le entregó el artículo de David Mermin, donde se atribuía con toda claridad a Geenberger, Horne y Zeilinger la prueba que en él se describía de que la mecánica cuántica era incompatible con las variables ocultas en un sentido fuerte en el caso de tres partículas entrelazadas. Antes de saberlo, Mike estuvo recibiendo correspondencia de la comunidad científica felicitándolo por el éxito de GHZ. El 25 de noviembre de 1990, John Clauser le envió una postal desde Berkeley:

Entre las felicitaciones había algunas de personas que estaban en la cima de la profesión, incluyendo premios Nobel. Los tres físicos se dieron cuenta enseguida de que sería mejor publicar su investigación en una revista adecuada. Para hacerlo, invitaron a Abner Shimony a unirse a ellos, ya que había estado trabajando en las desigualdades de Bell desde el principio. En 1990, el artículo «El teorema de Bell sin desigualdades», de Greenberger, Horne, Shimony y Zeilinger, se publicó en el American Journal of Physics, aunque la idea del entrelazamiento de tres partículas y el teorema de Bell perfeccionado se sigue llamando GHZ.^[17.2]

El dispositivo de tres partículas para presentar el teorema de GHZ puede ser o bien una versión de espín o polarización del experimento, o bien una versión tipo entrelazamiento del haz. La versión de polarización del dispositivo experimental de GHZ se muestra en la figura siguiente.

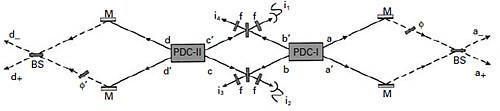
Lo más sorprendente del entrelazamiento de tres partículas, y la razón principal del interés que despertó la propuesta de GHZ, es que puede emplearse para probar el teorema de Bell sin el pesado uso de desigualdades.

Quedaba en pie la pregunta: ¿cómo crear tres fotones entrelazados en el laboratorio? Esto puede lograrse mediante una verdaderamente extraña propiedad cuántica, como se explica en la propuesta de Zeilinger y colaboradores de 1997. El diseño se muestra en la figura siguiente. Si dos pares de fotones entrelazados se introducen en un cierto dispositivo experimental que hace que un miembro de un par sea indistinguible de un miembro del otro par, y se captura uno de los dos fotones indistinguibles, entonces los tres fotones restantes quedan entrelazados. Lo que resulta aquí increíble es que los fotones quedan entrelazados porque un observador externo no puede ya decir a cuál de los dos pares pertenecía el fotón capturado. Entonces, dejando aparte el fotón capturado, los otros tres están entrelazados. Zeilinger y colaboradores construyeron realmente un dispositivo así en 1999.

Hay versiones accesibles de la prueba de GHZ del teorema de Bell usando tres fotones entrelazados. David Mermin, los mismos GHZ y, recientemente, un libro de texto de Daniel Styer han presentado la argumentación de forma comprensible para lectores no especializados.

Estas tres argumentaciones son comprensibles por dos razones que tienen en común: primera, las predicciones cuánticas no se deducen, sino que simplemente se exponen, ahorrándose por tanto al lector las deducciones matemáticas; segunda, no se detallan todas las predicciones cuánticas, sino sólo las necesarias para la argumentación. La siguiente versión es de Mike Horne, quien la utilizó en mayo de 2001 en su «Distinguished Scholar Lecture» dada para el claustro y estudiantes del Stonehill College (Massachusetts). Se basa bastante en argumentos anteriores, con la simplificación adicional de que hace uso de la versión de entrelazamiento del haz de GHZ, evitando así utilizar espín o polarización. La argumentación expuesta aquí ha sido adaptada de la presentación de Mike con la amable autorización y ayuda de éste.

La figura inferior muestra el montaje de GHZ con haz entrelazado, el cual es claramente una generalización directa de la interferometría de dos partículas al caso de tres partículas. Un espejo semiplateado (BS) colocado en cada una de las tres posiciones puede disponerse en una de las dos posiciones, la izquierda (I) o la derecha (D). Los resultados experimentales dependen de estas disposiciones.

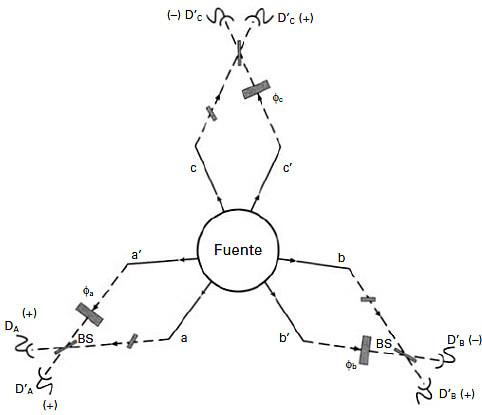
La figura presenta un montaje en el que una fuente muy especializada en el centro emite simultáneamente tres partículas entrelazadas. Puesto que estas partículas (o fotones) son objetos cuánticos, y están entrelazados, cada trío de partículas pasa a la vez a través de los agujeros a, b, c y de los agujeros a’, b’, c’. Mientras viajan a lo largo del diseño de «triple-diamante», cada partícula encuentra un separador de haz (un espejo semiplateado), que puede estar en la posición I o en la D.

La mecánica cuántica predice que, para cada partícula, los resultados (+) y (–) (que son los análogos a espín «arriba» o «abajo» para una partícula, o polarización vertical u horizontal para un fotón) se darán con la misma frecuencia: la mitad de las veces (+) y la otra mitad (–), independientemente de las posiciones de los separadores de haz. Si observamos pares de partículas, no veremos ningún patrón interesante: todos los pares de resultados (+,+), (–,–), (+,–) y (–,+) aparecerán con la misma frecuencia (una cuarta parte de las veces cada uno) para las partículas A y B (e igualmente para los otros pares B y C, y A y C), independientemente de las posiciones de los separadores de haz. Sin embargo, la mecánica cuántica predice que un observador vería una danza verdaderamente mágica si mirara lo que les sucede a las tres partículas. Por ejemplo, la mecánica cuántica predice que, si los separadores de haz para las partículas B y C se colocan ambos en la posición I, y las dos partículas acaban en, digamos, los detectores (–), y además el separador de haz para la partícula A se coloca en la posición D, entonces la partícula A acabará en el detector (+) con certeza. Ésta es una predicción notablemente fuerte, y existen otras similares para otros montajes. En la tabla siguiente se resumen los diversos montajes y las predicciones correspondientes de la mecánica cuántica:

Las predicciones de la derecha para las combinaciones particulares de la izquierda fueron obtenidas por Greenberger, Horne, Shimony y Zeilinger por medio de las matemáticas de la mecánica cuántica, aplicadas desde el principio al estado entrelazado de tres partículas. Como sabemos, el entrelazamiento es una superposición de estados, y para tres partículas, cada una de ellas pasando por dos aberturas, dicha superposición de estados puede escribirse, de una forma algo simplificada, como:

(abc + a’b’c’)

Esta ecuación es la expresión matemática del entrelazamiento de tres partículas, en donde el signo «+» encierra la propiedad «ambas-y» antes mencionada.

A partir de esta ecuación, que describe la superposición de estados —esto es, describe de forma matemática lo que significa el hecho de que tres partículas estén entrelazadas en el contexto específico de este experimento con seis aberturas—, los físicos desarrollan el aparato matemático y deducen las predicciones que se muestran en la tabla anterior. Los detalles precisos pueden encontrarse en el apéndice del artículo «Bell’s theorem without inequalities» (El teorema de Bell sin desigualdades), de Greenberger, Horne, Shimony y Zeilinger (American Journal of Physics, 58 [12], diciembre de 1990). Nótese que incluso en su artículo científico, los autores relegan su deducción algebraica basada en la ecuación del estado a un apéndice; era demasiado larga y es mecánica cuántica elemental. El lector interesado y amante de las matemáticas puede buscar esos detalles allí. Lo que es importante que comprenda el lector es que las predicciones de la tabla anterior son exactamente lo que la mecánica cuántica nos dice que sucederá en cada una de las situaciones. Tales predicciones se obtienen simplemente mediante la aplicación de las reglas de la mecánica cuántica a un montaje particular y al estado entrelazado de las tres partículas. Consideraremos, pues, válidas esas predicciones, consecuencia directa del entrelazamiento de las tres partículas.

Volviendo a la mencionada tabla, podemos observar que: dadas las posiciones de los separadores de haz (I o D) y los resultados específicos para B y C, el resultado para la partícula A puede predecirse con absoluta certeza. Por ejemplo, supongamos que los separadores de haz para las partículas B y C están ambos en la posición I y que la partícula B llega al detector (–), entonces, si el separador de haz de la partícula A está en la posición D, la partícula A irá con certeza al detector (+). Existen correlaciones perfectas análogas, como puede deducirse de la tabla, para otras elecciones para los separadores de haz y otros resultados para dos partículas. Dicho en pocas palabras: dadas las posiciones de los separadores de haz (I o D) y los resultados específicos para B y C, el resultado para la partícula A puede predecirse con absoluta certeza.

Ahora viene la parte importante del trabajo de GHZ. Para entender qué es ello y por qué el estado de GHZ proporciona una demostración tan convincente del teorema de Bell, así como una extensión del mismo, hemos de volver a lo que dijeron Einstein y sus colegas cincuenta y cinco años atrás, en el artículo de EPR de 1935.

Einstein y sus colaboradores observaron las correlaciones asombrosamente perfectas presentes en el entrelazamiento de dos partículas. Sostuvieron que esas correlaciones perfectas causan perplejidad, a no ser que revelen simplemente propiedades preexistentes, objetivamente reales de los objetos entrelazados. Afirmaron su adhesión a la existencia de una realidad objetiva como sigue (en el artículo de EPR de 1935): «Si, sin perturbar en modo alguno un sistema, podemos predecir con certeza el valor de una cantidad física, entonces existe un elemento de realidad física correspondiente a esa cantidad física».

Ahora bien, la llegada de la partícula A en su detector (+) es un «elemento de realidad» de acuerdo con la definición de Einstein, porque podemos predecir que esto sucederá con certeza, y claramente no perturbamos la partícula A por nuestra elección de los montajes de los separadores de haz en lugares distantes B y C. El resultado de A puede como mucho depender del montaje del separador de haz en la «estación» A, no en B o C. De modo que la llegada de la partícula A al detector (+) es un «elemento de realidad», llamémoslo A(D). Por consiguiente, A(D) es un elemento de realidad en la localización A, el cual muestra el resultado en la estación A cuando el separador de haz que controla la partícula A se ha dispuesto en la posición derecha (D). Para el resultado específico de que la partícula A llega al detector (+), decimos que el elemento de realidad es +1 y lo escribimos como: A(D) = +1. Análogamente para otras localizaciones y combinaciones de posiciones de los separadores de haz, tenemos, siguiendo a Einstein, finalmente seis elementos de realidad: A(D), B(D), C(D), A(I), B(I) y C(I). Cada uno de ellos puede valer +1 o –1.

Veamos ahora el teorema de GHZ.

Supongamos que los elementos de realidad de Einstein verdaderamente existen y son capaces de explicar las de otra manera desconcertantes predicciones mecánico-cuánticas dadas en la tabla anterior (las cuales han sido ya verificadas mediante un experimento de entrelazamiento de tres partículas realizado por Zeilinger en 1999). El acuerdo con las predicciones 1, 2, 3 y 4 de dicha tabla impone las siguientes restricciones sobre los elementos de realidad:

Estas igualdades son ciertas por lo siguiente. En el caso (1) las posiciones de los separadores de haz son DII y, según la mecánica cuántica, como se ve en la tabla, «o 0 o 2 partículas van a (–)». Entonces, o bien ninguno o dos elementos de realidad A(D), B(I) y C(I) son iguales a –1. Y cuando se multiplican los tres, se obtiene: 1 × 1 × 1 = 1 (en el caso de que ninguna de las partículas va a (–1) y 1 × (–1) × (–1) = 1 (para el caso en que dos partículas vayan a (–1), sin importar el orden). Análogamente, para los casos (2) y (3) se obtiene que el producto de los elementos de realidad es igual a 1, bien porque todos ellos sean iguales a 1 (ninguna partícula va a (–1)) o porque dos de ellos valen (–1) (el caso en que dos partículas van a (–1) y el tercero es +1).

En el caso (4) la predicción cuántica es que o 1 o 3 partículas van a –1. Entonces los productos posibles de los tres elementos de realidad A(D), B(D) y C(D) son: –1 × 1 × 1, o bien –1 × (–1) × (–1), y en ambos casos el resultado es –1.

Ahora llega el gran truco: multiplicar (todas) las tres primeras ecuaciones. La multiplicación de los miembros de la izquierda da:

A(D) A(I) A(I) B(I) B(D) B(I) C(I) C(I) C(D) = A(D) B(D) C(D)

La razón de que esta última igualdad sea cierta es que cada uno de los términos de la izquierda que no están en la derecha aparecen en la izquierda dos veces, y, por lo tanto, su producto es siempre +1 porque (+1 × +1 = +1; –1 × –1 = +1).

Ahora, multiplicando los miembros de la derecha de las ecuaciones (1), (2) y (3) se obtiene +1 × +1 × +1 = +1, así que tenemos: A(D) B(D) C(D) = +1.

Pero la predicción mecánico-cuántica, ecuación (4), dice que A(D) B(D) C(D) = –1.

Hemos llegado entonces a una contradicción. Por tanto, los «elementos de realidad» y la localidad de Einstein no pueden existir si la mecánica cuántica es correcta. Las variables ocultas son imposibles en el marco de la mecánica cuántica. Las partículas entrelazadas no actúan del modo en que lo hacen porque estén «preprogramadas» de alguna manera. Tal programación es imposible si las partículas se comportan según las reglas de la teoría cuántica. El teorema hace ver que cualesquiera conjuntos de instrucciones que pudieran poseer las partículas deben ser internamente inconsistentes y, por lo tanto, son imposibles. Las partículas responden instantáneamente a través de cualquier distancia que las separe a fin de proporcionarnos los resultados que la teoría cuántica afirma que se obtendrán. Ésa es la magia del entrelazamiento.

Además, los experimentos han probado que la teoría cuántica es cierta, y por tanto el realismo local de Einstein no lo es. El teorema de GHZ muestra la contradicción de una manera más directa y más fácil de entender (y sin carácter estadístico) en comparación con el teorema original de Bell.

«En todo nuestro trabajo nunca ha habido competición alguna. Ha sido maravilloso», recordaba Mike Horne al describirme su trabajo con sus colegas hasta llegar al diseño de GHZ y el descubrimiento del estado entrelazado de tres partículas de GHZ. «Tuvimos la suerte de trabajar en un campo en el que estaba trabajando muy poca gente, y entonces todo el mundo daba la bienvenida a quienes estaban interesados en los mismos problemas de los fundamentos de la mecánica cuántica», dijo.

Estos físicos, trabajando en armonía, hicieron una contribución muy importante a la física moderna. Su trabajo se desarrollaría y extendería en los años siguientes, y ayudaría a crear nuevas tecnologías que únicamente algunos escritores de ciencia ficción podrían haber imaginado tan sólo unos años antes.

Los anillos de Borromeo se llaman así a causa de la familia Borromeo, cuyos miembros pertenecen a la nobleza italiana. Esta familia es dueña de las bellas islas de Borromeo en el lago Maggiore, en el norte de Italia. El escudo de armas de la familia consta de tres anillos entrelazados de un modo interesante: si uno se rompe, los otros dos ya no siguen enlazados. Estos anillos tal vez representan la idea de «unidos, nos mantenemos de pie; divididos, nos derrumbamos». El físico P. K. Aravind, que ha estudiado el entrelazamiento, ha descubierto ciertas conexiones entre estados cuánticos entrelazados y diversas clases de nudos topológicos. En particular, Aravind ha sostenido que existe una correspondencia biunívoca entre el estado entrelazado de GHZ y los anillos de Borromeo, los cuales se muestran a continuación.^[17.3]

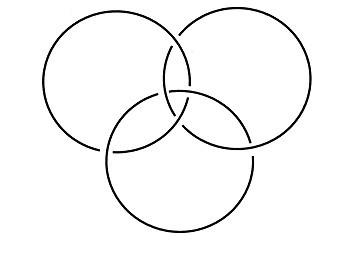
La prueba de Aravind tiene que ver con el entrelazamiento según una dirección particular del espín (la dirección z). También ha demostrado que si se mide el espín de las partículas entrelazadas según otra dirección, la dirección x, el estado entrelazado es diferente. Ahora ya no es análogo a los anillos de Borromeo, sino a los anillos de Hopf. Los tres anillos de Hopf están trabados entre sí de tal manera, que si se corta uno de ellos, los otros dos permanecen trabados. Los tres anillos de Hopf se muestran en la figura siguiente.

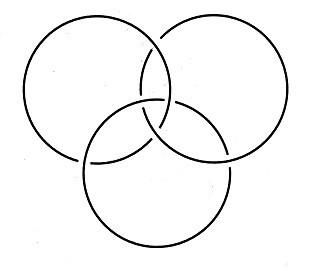
Aravind también ha probado que un estado de GHZ general de n partículas entrelazadas puede verse como una generalización de los tres anillos de Borromeo. Un enlazamiento así de varias partículas es análogo a una cadena enlazada con un aspecto como el de los anillos en la figura siguiente.

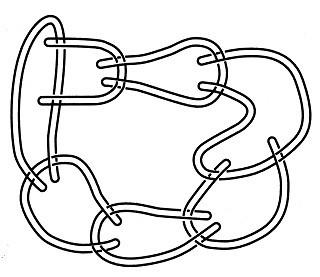
Danny Greenberger todavía visita en ocasiones a Mike Horne en Boston y en ocasiones a Anton Zeilinger en Viena, manteniendo así vivo el entrelazamiento entre estos tres buenos amigos. En Austria, Danny pasa algún tiempo con el grupo de investigación de Anton en la Universidad de Viena, un grupo importante que lleva a cabo trabajos punteros en muy diversos aspectos del comportamiento cuántico y del entrelazamiento, incluida la teleportación. Recientemente, Danny asistió a una fiesta del grupo de investigación, y en ella conoció a la hija y al nieto (de otra madre) de Schrödinger. El joven, miembro del grupo de investigación, no había descubierto que el gran físico era su abuelo hasta que fue adulto y se hizo él mismo físico.