8.

Il sistema del mondo

L’invenzione del calcolo infinitesimale

Lo sviluppo che da solo ha avuto la più grande influenza nella storia della matematica è stato il calcolo infinitesimale, inventato in maniera indipendente nel 1680 circa da Isaac Newton e Gottfried Leibniz. Quest’ultimo pubblicò per primo, ma Newton, incitato da alcuni amici con un esagerato amor di patria, rivendicò la precedenza e tacciò Leibniz di plagio. La contesa inasprì le relazioni tra i matematici inglesi e quelli dell’Europa continentale per un secolo, e gli inglesi furono i principali perdenti.

Il sistema del mondo

Anche se la precedenza spetta forse a Leibniz, Newton trasformò il calcolo infinitesimale in una tecnica fondamentale nel campo appena nato della fisica matematica, la via più nota e più efficace per l’umanità di comprendere il mondo naturale. Newton definì la sua teoria come «il sistema del mondo». Può sembrare una definizione poco modesta, ma era abbastanza corretta. Prima di Newton, la comprensione da parte dell’uomo dei modelli naturali si limitava di fatto alle idee di Galileo sui corpi in moto, in particolare la traiettoria parabolica di un oggetto come una palla di cannone, e alla scoperta di Keplero dell’orbita ellittica di Marte nel cielo. Dopo Newton, i modelli matematici regolavano quasi ogni fenomeno nel mondo fisico: il moto dei corpi terrestri e celesti, il flusso di aria e acqua, la trasmissione di calore, luce e suono, e la forza di gravità.

Stranamente, però, la più importante pubblicazione di Newton sulle leggi matematiche della natura, i Principia mathematica, non fa alcun riferimento al calcolo infinitesimale: si fonda invece su un’ingegnosa applicazione della geometria alla maniera degli antichi greci. Ma le apparenze ingannano: alcuni documenti inediti noti come i Portsmouth Papers mostrano che mentre lavorava ai Principia, Newton aveva già concepito l’idea alla base del calcolo infinitesimale. È probabile che Newton avesse usato i metodi del calcolo infinitesimale per giungere ad alcune delle sue scoperte, ma avesse scelto di non presentarle in quella maniera. La sua versione del calcolo infinitesimale fu pubblicata dopo la sua morte nell’opera The Method of Fluxions, nel 1732.

Il calcolo infinitesimale

Che cos’è il calcolo infinitesimale? I metodi di Newton e Leibniz si comprendono più facilmente se anticipiamo le idee di base. Il calcolo infinitesimale è la matematica delle velocità istantanee di variazione: quanto rapidamente una data quantità varia in questo preciso istante? Vediamo un esempio fisico. Un treno viaggia lungo un binario: che velocità ha proprio adesso? Il calcolo infinitesimale si divide in due aree principali. Il calcolo differenziale fornisce metodi per calcolare le velocità di variazione, e ha molte applicazioni geometriche, in particolare per trovare la tangente a una curva. Il calcolo integrale fa l’opposto: data la velocità di variazione di una determinata quantità, ricava la quantità stessa. Le applicazioni geometriche del calcolo integrale comprendono la stima di aree e volumi. La scoperta più significativa è forse questa insospettata relazione tra due problemi di geometria classica in apparenza distinti: trovare la tangente a una curva e calcolare un’area.

Il calcolo infinitesimale studia le funzioni: procedimenti che si applicano a un numero e determinano un altro numero a questo associato. Il procedimento è in genere definito da una formula, che assegna a un dato numero x (possibilmente in un intervallo specificato) un numero associato f(x). Esempi sono la funzione radice quadrata (che richiede che x sia positivo) e la funzione quadrato f(x) = x² (dove non ci sono vincoli su x).

La prima idea alla base del calcolo infinitesimale è la differenziazione, che calcola la derivata di una funzione. La derivata è la velocità con cui f(x) varia, confrontata con la variazione di x: la velocità di variazione di f(x) rispetto a x.

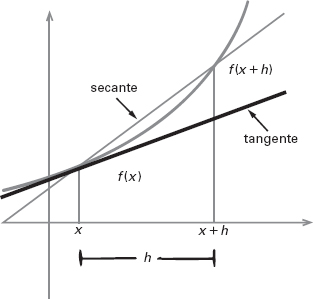
In termini geometrici, la velocità di variazione è la pendenza della tangente al grafico di f in corrispondenza del valore x. Si può approssimare trovando la pendenza della secante, una retta che taglia il grafico di f in due punti vicini, corrispondenti a x e x + h, rispettivamente, dove h è piccolo. La pendenza della secante è

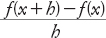
Supponiamo ora che h diventi molto piccolo. In questo caso la secante si avvicina alla tangente del grafico in x. In un certo senso dunque la pendenza richiesta (la derivata di f in x) è il limite di questa espressione quando h diventa piccolo a piacere.

Proviamo a eseguire questo calcolo con un semplice esempio, f(x) = x². Ora

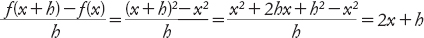
Quando h diventa molto, molto piccolo, la pendenza 2x + h si avvicina sempre più a 2x. La derivata di f è dunque la funzione g per cui g(x) = 2x.

Il concetto fondamentale è la definizione di limite, e ci volle più di un secolo per trovare una definizione logica.

L’altra idea fondamentale nel calcolo infinitesimale è quella di integrazione. Questo concetto si può comprendere molto facilmente come il procedimento inverso della differenziazione. L’integrale di g quindi, scritto

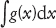
è la funzione f(x) che ha come derivata g(x). Per esempio, dal momento che la derivata di f(x) = x² è g(x) = 2x, l’integrale di g(x) = 2x è f(x) = x².

In simboli

Figura 8.1

Geometria delle approssimazioni alla derivata.

La necessità del calcolo infinitesimale

L’ispirazione per l’invenzione del calcolo infinitesimale venne da due direzioni. Nell’ambito della matematica pura, il calcolo differenziale si sviluppò a partire dai metodi per trovare la tangente a una curva, e il calcolo integrale si sviluppò a partire dai metodi per calcolare le aree delle figure piane e il volume di solidi. La spinta principale per il calcolo infinitesimale venne però dalla fisica, dalla convinzione sempre più radicata del fatto che la natura presenti modelli regolari. Per ragioni che ancora non comprendiamo pienamente, molti dei modelli fondamentali in natura implicano qualche velocità di variazione. E questi valori hanno senso, e possono essere scoperti, soltanto per mezzo del calcolo infinitesimale.

Prima del Rinascimento, il modello più accurato per il movimento del Sole, della Luna e dei pianeti era quello concepito da Tolomeo. In questo modello, la Terra era fissa, e tutto il resto, in particolare il Sole, le girava attorno in un sistema di circonferenze (reali o immaginarie, a seconda della tendenza). Le circonferenze nascevano come sfere nel lavoro dell’astronomo greco Ipparco; le sue sfere ruotavano attorno a giganteschi assi, e alcune di esse erano attaccate ad altre sfere insieme alle quali si muovevano. Questo tipo di moto composto sembrava necessario per modellare il movimento complesso dei pianeti. Ricordate che alcuni pianeti, come Mercurio, Venere e Marte, sembrano seguire complicate traiettorie che includono anelli chiusi. Altri – Giove e Saturno erano gli unici altri pianeti conosciuti all’epoca – si comportavano in maniera più tranquilla, ma anche questi corpi presentavano strane irregolarità, note sin dal tempo dei babilonesi.

Abbiamo già incontrato il sistema di Tolomeo, quello degli epicicli, che sostituiva le sfere con circonferenze, ma conservava il moto composto. Il modello di Ipparco non era molto accurato, confrontato con le osservazioni, mentre il modello di Tolomeo si adattava molto bene alle osservazioni, e per oltre un migliaio di anni fu considerato come la parola definitiva sulla questione. I suoi scritti, tradotti in arabo con il titolo di Almagesto, furono usati dagli astronomi di molte civiltà.

Dio e scienza

Neppure l’Almagesto comunque riusciva a rendere conto di tutti i moti planetari, e per di più era piuttosto complicato. Attorno all’anno 1000, uno sparuto numero di pensatori arabi ed europei cominciò a chiedersi se il movimento giornaliero del Sole potesse essere spiegato con una Terra in rotazione, e alcuni di essi indugiarono anche nell’idea che la Terra girasse attorno al Sole. A quel tempo però si ottenne poco da tali speculazioni.

Nell’Europa rinascimentale, invece, la pratica scientifica cominciò a radicarsi, e una delle prime vittime fu il dogma religioso. A quel tempo, la chiesa cattolica romana esercitava un pesante controllo sulla concezione dell’universo da parte dei suoi adepti. Non si trattava soltanto del fatto che l’esistenza dell’universo, e il suo dispiegarsi quotidiano, erano attribuiti al Dio cristiano. Il punto era che si credeva che la natura dell’universo riflettesse un’interpretazione molto letterale della Bibbia. La Terra era quindi vista come il centro di tutte le cose, il solido fondamento attorno al quale ruotavano i cieli. E gli esseri umani erano il punto più alto della creazione, la ragione per l’esistenza dell’universo.

Nessuna osservazione scientifica può mai confutare l’esistenza di un creatore invisibile e inconoscibile. Le osservazioni possono però – e lo fecero – smentire la concezione della Terra al centro dell’universo, e questo causò un enorme scombussolamento, e determinò la morte di molte persone innocenti, talvolta con metodi terribili e crudeli.

Copernico

Gli eventi precipitarono nel 1543, quando lo studioso polacco Niccolò Copernico (Mikołaj Kopernik) pubblicò un libro sorprendente, originale e per certi versi eretico: il De revolutionibus orbium coelestium. Come Tolomeo, egli usava gli epicicli per una maggiore accuratezza. Diversamente da Tolomeo, poneva al centro del sistema il Sole, mentre tutti gli altri corpi, compresa la Terra ma senza la Luna, giravano attorno al Sole. La Luna girava da sola attorno alla Terra.

La principale motivazione che aveva condotto Copernico a formulare questa ipotesi radicale era di carattere pragmatico: sostituiva i 77 epicicli con 34 soltanto. Tra gli epicicli immaginati da Tolomeo, c’erano molte ripetizioni di una circonferenza particolare: circonferenze con quella specifica dimensione, e velocità di rotazione, continuavano a presentarsi, associate con molti corpi celesti distinti. Copernico comprese che se tutti questi epicicli fossero stati trasferiti alla Terra, ne sarebbe bastato soltanto uno. Noi oggi interpretiamo questo risultato in termini dei moti planetari relativi alla Terra. Se per errore assumiamo che la Terra sia fissa, come potrebbe sembrare a un ingenuo osservatore, allora il movimento della Terra attorno al Sole viene trasferito a tutti i pianeti come un epiciclo aggiuntivo.

Un altro vantaggio della teoria di Copernico era che trattava tutti i pianeti esattamente nello stesso modo. Tolomeo aveva bisogno di meccanismi differenti per spiegare i pianeti interni e quelli esterni. Ora, l’unica differenza era che i pianeti più interni erano più vicini al Sole rispetto alla Terra, mentre i pianeti più esterni erano ancora più lontani. L’intera costruzione sembrava molto sensata, ma nel complesso fu respinta, per una varietà di motivi, non tutti di carattere religioso.

La teoria di Copernico era complicata, strana e il suo libro era difficile da leggere. Tycho Brahe, uno dei migliori osservatori astronomici dell’epoca, trovò alcune discrepanze tra la teoria eliocentrica di Copernico e alcune acute osservazioni, che pure erano in disaccordo con la teoria di Tolomeo: tentò alla fine di trovare un compromesso migliore.

Keplero

Quando Brahe morì, le sue carte furono ereditate da Johannes Kepler (detto Keplero), che impiegò anni a studiare le osservazioni, alla ricerca di una struttura o di un modello regolare. Keplero era una specie di mistico, nella tradizione pitagorica, e tendeva a sovrapporre modelli artificiali ai dati osservati. Il più famoso di questi maldestri tentativi di trovare regolarità nei cieli fu la sua meravigliosa ma completamente sbagliata spiegazione della spaziatura dei pianeti in termini di solidi regolari. Ai suoi tempi, i pianeti conosciuti erano sei in tutto: Mercurio, Venere, Terra, Marte, Giove e Saturno. Keplero si chiese se la loro distanza dal Sole seguisse un modello geometrico, e si chiese inoltre perché i pianeti erano sei. Notò che sei pianeti lasciavano spazio per cinque forme intermedie, e dal momento che erano noti esattamente cinque solidi regolari, questo poteva spiegare il limite di sei pianeti. Concepì una serie di sei sfere, poste una all’interno dell’altra, e identificò l’equatore di ogni sfera con l’orbita di un pianeta. Tra le sfere, annidati strettamente all’esterno di una sfera e all’interno della successiva, collocò i cinque solidi, nell’ordine

Mercurio
	Ottaedro
Venere
	Icosaedro
Terra
	Dodecaedro
Marte
	Tetraedro
Giove
	Cubo
Saturno

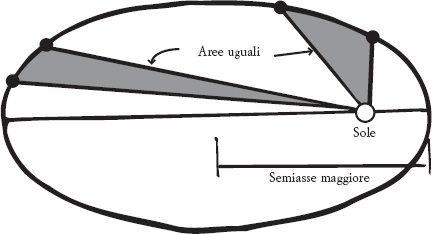
Figura 8.2

I pianeti si muovono lungo un dato intervallo di tempo.

I numeri andavano abbastanza bene, soprattutto considerata la limitata accuratezza delle osservazioni a quei tempi. Esistono però 120 modi diversi per disporre i cinque solidi, e di conseguenza abbiamo tantissime spaziature differenti. È abbastanza sorprendente che in un caso si ottenesse un accordo molto vicino con la realtà. La successiva scoperta di altri pianeti diede un duro colpo alla ricerca di un modello regolare in questa direzione, relegandola tra i rifiuti della storia.

Nel frattempo, comunque, Keplero aveva scoperto alcune regole che sono valide ancora oggi, e sono note come leggi di Keplero del moto planetario. Le aveva derivate, dedicando circa vent’anni ai calcoli necessari, dalle osservazioni di Brahe su Marte. Le leggi affermano:

(i) i pianeti si muovono attorno al Sole in orbite ellittiche;

(ii) i pianeti percorrono aree uguali in tempi uguali;

(iii) il quadrato del periodo di rivoluzione di ogni pianeta è proporzionale al cubo della sua distanza media dal Sole.

La caratteristica più originale del lavoro di Keplero consiste nella rinuncia alla circonferenza classica (ritenuta la forma più perfetta possibile) in favore dell’ellisse. Keplero lo aveva fatto con una certa riluttanza, convincendosi di aver scelto l’ellisse dopo aver eliminato tutte le altre forme. Non c’è una particolare ragione per aspettarsi che queste tre leggi riflettano una relazione più stretta con la realtà rispetto all’ipotetica configurazione di solidi regolari, ma come accadde, le tre leggi rivelarono una reale importanza scientifica.

Galileo

Un’altra figura di spicco del periodo fu Galileo Galilei, che scoprì alcune regolarità matematiche nel moto di un pendolo e nei corpi in caduta libera. Nel 1589, professore di matematica all’Università di Pisa, condusse diversi esperimenti sui corpi in caduta lungo un piano inclinato, ma non pubblicò i suoi risultati. Fu in questo periodo che comprese l’importanza degli esperimenti controllati nello studio dei fenomeni naturali, un’idea che è ora fondamentale in tutta la scienza. Si occupò di astronomia, producendo una serie di scoperte fondamentali, che alla fine lo condussero ad abbracciare la teoria copernicana eliocentrica. Questo lo mise in contrasto con la Chiesa, tanto che alla fine fu processato per eresia e condannato agli arresti domiciliari.

Durante gli ultimi anni di vita, ormai malato, scrisse i Discorsi e dimostrazioni matematiche intorno a due nuove scienze, dove spiegava i suoi studi sul moto dei corpi lungo un piano inclinato. Affermò che la distanza percorsa da un corpo in principio stazionario e soggetto ad accelerazione uniforme è proporzionale al quadrato del tempo. Questa legge è alla base della sua scoperta precedente in merito alla traiettoria parabolica seguita da un proiettile. Insieme alle leggi di Keplero del moto planetario, aprì la via a una nuova materia, la meccanica, lo studio matematico dei corpi in movimento.

Queste sono le basi fisiche astronomiche che condussero al calcolo infinitesimo. In seguito, approfondiremo le basi matematiche.

L’invenzione del calcolo infinitesimale

L’invenzione del calcolo infinitesimale fu il risultato di una serie di ricerche precedenti su quelli che sembrano problema lontani, ma rivelano in realtà un’omogeneità nascosta. Tra questi vi erano il calcolo della velocità istantanea di un oggetto in moto a partire dalla distanza percorsa in un tempo determinato, il calcolo della tangente a una curva, il calcolo della lunghezza di una curva, la determinazione dei valori massimi e minimi di una quantità variabile, il calcolo dell’area di una certa figura nel piano e il volume di un determinato solido nello spazio. Alcuni importanti concetti ed esempi furono sviluppati da Fermat, Descartes e un inglese meno famoso, Isaac Barrow, ma i metodi si limitavano a problemi particolari. Era necessario un metodo generale.

Leibniz

Il primo vero passo avanti fu compiuto da Gottfried Wilhelm Leibniz, un avvocato di professione, che aveva dedicato gran parte della sua vita alla matematica, alla logica, alla filosofia, alla storia e a molte branche della scienza. Intorno al 1637 cominciò a dedicarsi al problema classico di trovare la tangente a una curva, e notò che questo era di fatto il problema inverso rispetto alla ricerca di aree e volumi. L’ultimo si riduceva a trovare una curva date le sue tangenti; il primo problema era esattamente il contrario.

Leibniz usò questo collegamento per definire che cosa erano, in realtà, gli integrali, usando l’abbreviazione omn (da omnia, il termine latino per «tutto»). Nei suoi manoscritti troviamo infatti formule come

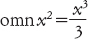
Nel 1675 sostituì omn con il simbolo ∫ usato ancora oggi, che è una lettera s allungata, per indicare la somma. Lavorò in termini di piccoli incrementi dx e dy alle quantità x e y, e usò il loro rapporto dx/dy per determinare la velocità di variazione di y in funzione di x. Di fatto, se f è una funzione allora Leibniz scriveva

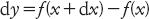
in modo che

che è la normale approssimazione secante alla pendenza della tangente.

Leibniz sapeva che questa notazione presenta alcuni problemi: se dy e dx sono diversi da zero, allora dy/dx non è la velocità istantanea di variazione di y, ma un’approssimazione. Tentò di aggirare questo problema assumendo dx e dy piccoli in maniera infinitesima. Un infinitesimo è un numero diverso da zero che è più piccolo di qualunque altro numero diverso da zero. Purtroppo, è facile vedere che un numero del genere non può esistere (la metà di un infinitesimo è sempre un numero diverso da zero, ma più piccolo), e dunque questo modo di affrontare il problema non fa altro che spostare il problema altrove.

Nel 1676 Leibniz sapeva come integrare e differenziare qualunque potenza di x, scrivendo la formula

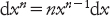
che noi scriveremmo ora come

Nel 1677 derivò regole per differenziare la somma, il prodotto e il quoziente di due funzioni, e nel 1680 ricavò la formula per la lunghezza di un arco di curva, e il volume di un solido di rivoluzione, come integrali di varie quantità collegate.

Anche se conosciamo questi eventi, e le date associate, dai suoi manoscritti inediti, Leibniz pubblicò per la prima volta le sue idee sul calcolo infinitesimale soltanto in seguito, nel 1684. Jakob e Johann Bernoulli trovarono questo lavoro piuttosto oscuro, e lo descrissero come «un enigma piuttosto che una spiegazione». A posteriori, sappiamo che a quel tempo Leibniz aveva scoperto una parte importante delle fondamenta del calcolo infinitesimale, con applicazioni a curve complicate come la cicloide, e aveva una buona comprensione di concetti come la curvatura. Purtroppo, i suoi scritti erano frammentari e di fatto illeggibili.

Newton

L’altro padre del calcolo infinitesimale fu Isaac Newton. Due dei suoi amici, Isaac Barrow ed Edmond Halley, ne riconobbero le notevoli abilità, e lo incoraggiarono a pubblicare il suo lavoro. Newton non amava le critiche, e quando nel 1672 pubblicò le sue teorie sulla luce, il suo lavoro attirò moltissime obiezioni, che rinsaldarono la sua riluttanza ad affidare alle stampe i propri pensieri. Nonostante questo, continuò a pubblicare in maniera sporadica, e scrisse due libri. In privato continuò a sviluppare la sua teoria della gravità, e nel 1684 Halley tentò di convincerlo a pubblicare il lavoro. A parte il generale atteggiamento di rifiuto di Newton nei confronti delle critiche, c’era però un ostacolo tecnico. Era stato costretto a modellare i pianeti come particelle puntiformi, con massa diversa da zero ma dimensione nulla, e questo a suo parere era irrealistico e avrebbe suscitato molte obiezioni. Avrebbe voluto sostituire questi punti irrealistici con sfere solide, ma non era in grado di dimostrare che l’attrazione gravitazionale di una sfera è uguale a quella di una particella puntiforme della stessa massa.

Nel 1686 riuscì a colmare la lacuna, e nel 1687 i Principia videro la luce. L’opera conteneva molte idee innovative. Le più importanti riguardavano le leggi matematiche del moto, che estendevano il lavoro di Galileo, e la gravità, fondata sulle leggi formulate da Keplero.

La principale legge del moto di Newton (ne esistono altre secondarie) afferma che l’accelerazione di un corpo in movimento, moltiplicata per la sua massa, è uguale alla forza che agisce sul corpo. Ora, la velocità è la derivata della posizione, e l’accelerazione è la derivata della velocità. Di conseguenza, anche solo per enunciare la legge di Newton, occorre la derivata seconda (la derivata della derivata) della posizione rispetto al tempo, che noi scriviamo come

Newton aggiungeva invece due puntini sopra la

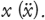
La legge di gravità afferma che due particelle di materia si attraggono reciprocamente con una forza che è proporzionale alle loro masse, e inversamente proporzionale al quadrato della distanza che le separa. Così, per esempio, la forza che attrae la Terra alla Luna si ridurrebbe a un quarto se la Luna fosse spostata al doppio della distanza, o a un nono se la distanza fosse triplicata. Di nuovo, poiché riguarda le forze, la legge implica la derivata seconda della posizione.

Newton dedusse questa legge dalle tre leggi di Keplero sul moto dei pianeti. La deduzione pubblicata era un capolavoro di geometria euclidea. Newton scelse questo stile di presentazione perché si basava su una matematica familiare, che non poteva essere criticata facilmente. Molti aspetti dei Principia devono però la loro genesi all’invenzione mai pubblicata del calcolo infinitesimale da parte di Newton.

Tra i primi lavori di Newton sull’argomento c’era un articolo intitolato De analysi per aequationes numero terminorum infinitas, che fece circolare tra alcuni corrispondenti nel 1669. Nella terminologia moderna, Newton si chiedeva che cos’è l’equazione di una funzione f(x), se l’area sotto il grafico è della forma x^m. (In realtà chiedeva qualcosa di più generale, ma facciamola semplice). Dedusse, per soddisfazione personale, che la risposta era f(x) = mx^m−l.

L’approccio di Newton al calcolo della derivata era più simile a quello di Leibniz, tranne per il fatto che egli usava o al posto di dx, e dunque il suo metodo sconta lo stesso problema logico: sembra soltanto un’approssimazione. Newton riuscì, però, a dimostrare che assumendo o molto piccolo, l’approssimazione era ancora migliore. Al limite, quando o diventa piccolo a piacere, l’errore scompare. Newton sosteneva, dunque, che il suo risultato finale fosse esatto. Introdusse un nuovo termine, flussione, per esprimere il concetto fondamentale, quello di una quantità che fluisce verso lo zero ma non assume mai questo valore.

Nel 1671, scrisse una trattazione più estesa, il Methodus fluxionum et serierum infinitorum. Il primo libro sul calcolo infinitesimale non fu pubblicato fino al 1711; il secondo apparve nel 1736. È chiaro che alla data del 1671 Newton aveva già sviluppato la maggior parte dei concetti fondamentali sul calcolo infinitesimale.

Gli oppositori di questo procedimento, e in particolare il vescovo George Berkeley nel suo libro del 1734 The Analyst, a Discourse Addressed to an Infidel Mathematician, sottolinearono come fosse illogico dividere numeratore e denominatore per o se in seguito si pone o uguale a 0. In effetti, il procedimento nasconde che la frazione è in realtà 0/0, e com’è noto non ha senso. Newton rispose che di fatto egli non aveva posto o uguale a 0: egli calcolava quello che succedeva quando o si avvicinava a piacere a 0 ma senza mai assumere quel valore. Il metodo riguardava le flussioni, non i numeri.

I matematici cercarono riparo nelle analogie fisiche (Leibniz parlava dello «spirito di finezza» contrapposto allo «spirito della logica») ma Berkeley aveva perfettamente ragione. Ci volle più di un secolo per trovare una risposta valida alle sue obiezioni, con la definizione del concetto intuitivo di «passaggio al limite» in una maniera rigorosa. Il calcolo infinitesimo si tramutò poi in un argomento più raffinato, l’analisi. Per un secolo, però, dopo l’invenzione del calcolo, nessuno tranne Berkeley si preoccupò molto delle fondamenta logiche, e il calcolo infinitesimo si diffuse nonostante questa lacuna.

Si diffuse perché Newton aveva ragione, ma ci vollero circa duecento anni prima che il suo concetto di flussione fosse formulato in una maniera accettabile dal punto di vista logico, in termini di limiti. Fortunatamente per la matematica, il progresso non si fermò prima della scoperta di un fondamento logico accettabile. Il calcolo infinitesimale era troppo utile, e troppo importante, per essere frenato da qualche cavillo logico. Berkeley era infuriato, e sosteneva che il metodo sembrava funzionare soltanto perché i diversi errori si cancellavano l’un l’altro. Aveva ragione, ma non ebbe la prontezza di chiedere perché si cancellavano comunque. Perché se accadeva così, allora non erano veri errori!

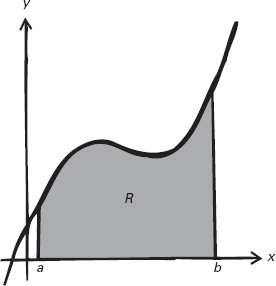
La differenziazione è associata con il suo processo inverso, l’integrazione. L’integrale di f(x), scritto ∫f(x)dx, è la funzione che ha come derivata f(x). In termini geometrici, esso rappresenta l’area compresa sotto il grafico della funzione f. L’integrale definito 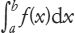è l’area compresa sotto questo grafico e limitata tra i valori x = a e x = b.

Le derivate e gli integrali risolsero problemi che in passato avevano messo a dura prova l’ingegnosità dei matematici. Velocità, tangenti, massimi e minimi potevano tutti essere trovati usando la differenziazione. Lunghezze, aree e volumi potevano essere calcolati tramite l’integrazione. C’era però molto di più. Inaspettatamente, sembrava che i modelli e le regolarità della natura fossero scritti nel linguaggio del calcolo infinitesimale.

L’inglese rimane indietro

Quando l’importanza del calcolo infinitesimale si fece ancora più evidente, maggiore prestigio ne derivò per il suo inventore. Ma chi era l’inventore?

Abbiamo visto che Newton iniziò a concepire il calcolo infinitesimale nel 1665, ma non pubblicò nulla sull’argomento fino al 1687. Leibniz, le cui linee di pensiero erano molto vicine a quelle di Newton, aveva iniziato a studiare la questione nel 1673, per pubblicare i primi lavori in merito nel 1684. I due lavorarono in maniera indipendente, ma Leibniz potrebbe aver appreso degli studi di Newton in occasione di un viaggio a Parigi nel 1672 e a Londra nel 1673: Newton aveva inviato una copia del suo De analysi a Barrow nel 1669, e Leibniz aveva parlato con diverse persone che pure conoscevano Barrow, e potevano quindi essere venute a conoscenza di questo lavoro.

Quando Leibniz pubblicò il suo lavoro nel 1684, alcuni degli amici di Newton si offesero (forse perché Newton era stato anticipato nella pubblicazione e avevano compreso troppo tardi la posta in gioco) e accusarono Leibniz di aver rubato le idee dell’inglese. I matematici continentali, soprattutto i Bernoulli, presero le parti di Leibniz, sostenendo che colpevole di plagio fosse Newton, e non Leibniz. A dire il vero, entrambi erano giunti alla scoperta in maniera del tutto indipendente, come mostrano i loro manoscritti inediti; per confondere le acque, entrambi avevano tratto molto materiale da un lavoro precedente di Barrow, che forse aveva maggiori motivi di risentimento nei confronti di entrambi.

Figura 8.3

L’integrale definito.

Le accuse avrebbero potuto essere lasciate cadere facilmente, ma la disputa si fece invece più accesa: Johann Bernoulli estese la sua avversione da Newton all’intera nazione inglese. Il risultato finale fu un disastro per la matematica inglese, perché in Inghilterra i matematici rimasero tenacemente fedeli alla concezione geometrica di Newton, che era difficile da usare, mentre gli analisti continentali adottarono i metodi algebrici di Leibniz, più formali, e portarono avanti l’argomento a grande velocità. La maggior parte dei risultati in fisica matematica si dovette quindi a francesi, tedeschi, svizzeri e olandesi, mentre la matematica inglese rimase a languire.

L’equazione differenziale

Il concetto più importante che emerse dalla messe di lavoro sul calcolo infinitesimale fu l’esistenza, e l’applicazione, di un nuovo tipo di equazione: l’equazione differenziale. Le equazioni algebriche mettono in relazione diverse potenze di un numero ignoto. Le equazioni differenziali sono più grandiose: mettono in relazione diverse derivate di una funzione incognita.

Le leggi del moto di Newton ci dicono che se y(t) è l’altezza di una particella in moto soggetta a gravità vicino alla superficie della Terra, allora la derivata seconda d²y/dt² è proporzionale alla forza g che agisce su di essa; in particolare

dove m è la massa della particella. Questa equazione non specifica direttamente la funzione y, ma una proprietà della sua derivata seconda. Dobbiamo risolvere l’equazione differenziale per trovare y. Due integrazioni successive portano alla soluzione

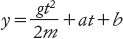
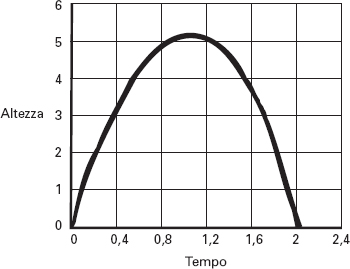
dove b è l’altezza iniziale della particella e a è la sua velocità iniziale. La formula ci dice che il grafico di altezza y rispetto al tempo t è una parabola sottosopra. Questa è l’osservazione di Galileo.

Gli sforzi pionieristici di Copernico, Keplero, Galileo e altri scienziati del Rinascimento condussero alla scoperta di modelli e regolarità matematiche nel mondo naturale. Alcune regolarità si rivelarono false, e furono abbandonate; altre fornirono modelli molto accurati della natura, e furono analizzate ancora e sviluppate. Da questi primi inizi, emerse il concetto che viviamo in un «universo a orologeria», che si muove secondo regole rigide e inevitabili, nonostante una dura opposizione religiosa, in particolare da parte della chiesa di Roma.

Figura 8.4

La traiettoria parabolica di un proiettile.

La meravigliosa scoperta di Newton era che i modelli della natura sembrano manifestarsi non come regolarità espresse in determinate quantità, ma come relazioni tra le loro derivate. Le leggi della natura sono scritte nel linguaggio del calcolo infinitesimale; quello che importa non sono i valori delle variabili fisiche, ma le velocità con cui queste cambiano. Fu una profonda intuizione, e determinò una rivoluzione, che condusse più o meno direttamente alla scienza moderna, e trasformò per sempre il nostro pianeta.