6.
Curve e coordinate
Geometria è algebra è geometria
Anche se di solito classifichiamo la matematica in aree separate, come aritmetica, algebra, geometria e così via, questa distinzione è più dovuta a questioni di nostra convenienza piuttosto che alla struttura stessa della materia. In matematica, non esistono confini netti e definiti tra aree apparentemente diverse, e i problemi che sembrano di pertinenza di un’area possono essere risolti usando i metodi propri di un’altra. In effetti, i principali progressi dipendono spesso dall’instaurarsi di un collegamento inatteso tra argomenti in precedenza distinti.
Fermat
La matematica greca ha tracce di tali connessioni, con collegamenti tra il teorema di Pitagora e i numeri irrazionali, e l’uso da parte di Archimede di analogie meccaniche per trovare il volume della sfera. La vera portata e influenza di tali contaminazioni incrociate divenne innegabile in un breve periodo dal 1620 al 1640. Durante quel breve periodo, due dei più importanti matematici a livello mondiale scoprirono un importante collegamento tra l’algebra e la geometria, e di fatto mostrarono che ognuna di queste aree può essere convertita nell’altra per mezzo di coordinate. Tutta la geometria di Euclide, e il lavoro dei suoi successori, può essere ridotta a calcoli algebrici. Al contrario, ogni concetto algebrico può essere interpretato in termini di geometria di curve e superfici.
Potrebbe sembrare che tali connessioni rendano superflua una delle due aree. Se tutta la geometria può essere sostituita dall’algebra, perché ci serve la geometria? La risposta è che ogni area ha il suo punto di vista caratteristico, che può all’occorrenza essere molto forte e potente. Qualche volta è meglio pensare in termini geometrici, e qualche volta il punto di vista algebrico è migliore.
La prima persona a parlare di coordinate fu Pierre de Fermat. Fermat è noto soprattutto per il suo lavoro sulla teoria dei numeri, ma si dedicò anche a molte altre aree della matematica, compresa la probabilità, la geometria e le applicazioni all’ottica. Nel 1620 circa Fermat stava tentando di comprendere la geometria delle curve, e iniziò ricostruendo, a partire dalle poche informazioni disponibili, un libro di Apollonio andato perduto, i Luoghi piani. In seguito, Fermat intraprese le sue ricerche; le mise per iscritto nel 1629 ma le pubblicò soltanto cinquant’anni dopo, con il titolo di Ad locos planos et solidos isagoge. Così facendo scoprì i vantaggi conseguenti alla riformulazione di concetti geometrici in termini algebrici.
Luogo, è un termine obsoleto oggi, ma era molto comune ancora nel 1960. Parliamo di luogo quando cerchiamo tutti i punti nel piano o nello spazio che soddisfano particolari condizioni geometriche. Per esempio, potremmo cercare il luogo di tutti i punti la cui distanza da due altri punti fissati dà come somma sempre lo stesso valore. Questo luogo è un’ellisse con i due punti come fuochi. Questa proprietà dell’ellisse era nota ai greci.
Fermat notò un principio generale: se le condizioni imposte sul punto possono essere espresse con una singola equazione con due incognite, il luogo corrispondente è una curva, o una linea retta, che consideriamo come un tipo speciale di curva per evitare distinzioni inutili. Fermat illustrò questo principio con un diagramma nel quale le due quantità incognite A ed E sono rappresentate come distanze in due direzioni distinte.
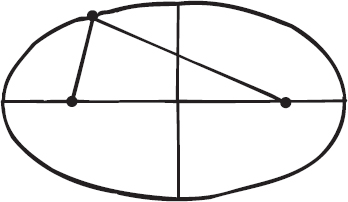
Figura 6.1
La proprietà dei fuochi di un’ellisse.
Figura 6.2
L’approccio di Fermat alle coordinate.
Egli elencò poi alcuni tipi particolari di equazione che mettevano in relazione A ed E, e spiegò quali curve rappresentavano. Per esempio, se A2 = 1 + E2, allora il luogo in questione è un’iperbole.
Nella terminologia moderna, Fermat introdusse assi obliqui nel piano (obliqui significa che non si incontrano necessariamente con un angolo retto). Le variabili A ed E sono le due coordinate, che noi chiameremmo x e y, di ogni punto dato rispetto a questi assi. Il principio di Fermat quindi afferma che qualunque equazione espressa in variabili a due coordinate definisce una curva, e i suoi esempi ci dicono quale tipo di equazioni corrispondono a quale tipo di curva, tracciando le curve tradizionali note ai greci.
Descartes
Il concetto moderno di coordinate ebbe la sua piena realizzazione nel lavoro di Descartes. Nella vita quotidiana, siamo abituati a spazi di due e tre dimensioni, e ci occorre un grande sforzo di immaginazione per prendere in considerazione altre possibilità. Il nostro sistema visivo fa sì che ognuno dei nostri occhi veda il mondo esterno come un’immagine bidimensionale, come la figura su uno schermo televisivo. Le immagini leggermente diverse provenienti dai due occhi sono combinate dal cervello per aggiungere un senso di profondità, attraverso il quale noi percepiamo il mondo circostante nelle sue tre dimensioni.
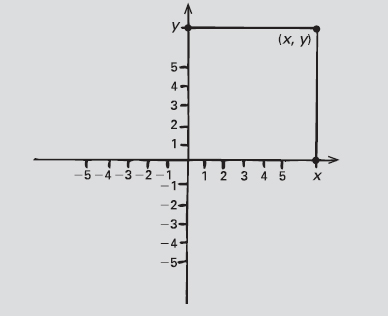
La chiave per visualizzare gli spazi multidimensionali è quella di pensare a un sistema di coordinate, che fu introdotto da Descartes in un’appendice annessa al suo libro Discours de la méthode e intitolata La géométrie. La sua idea è che la geometria del piano possa essere reinterpretata in termini algebrici, e questa impostazione è di fatto analoga a quella di Fermat. Scegliamo un punto nel piano e lo identifichiamo come l’origine. Tracciamo due assi, cioè rette che passano attraverso l’origine e si incontrano ad angolo retto. Indichiamo un asse con il simbolo x e l’altro con il simbolo y. Ora, ogni punto P nel piano è determinato dalla coppia di valori (x, y) che indicano le distanze del punto dall’origine, parallelamente rispetto all’asse x e y.
René Descartes (1596-1650)
Descartes iniziò a studiare matematica nel 1618, come allievo dello scienziato olandese Isaac Beeckman. Lasciò l’Olanda per viaggiare in Europa, e si unì all’esercito bavarese nel 1619. Continuò a viaggiare tra il 1620 e il 1628, visitando la Boemia, l’Ungheria, la Germania, l’Olanda, la Francia e l’Italia. Nel 1622, a Parigi, incontrò Mersenne, con il quale in seguito intrattenne una regolare corrispondenza. Mersenne lo mise anche in contatto con la maggior parte dei più eminenti studiosi del tempo.
Nel 1628, Descartes si trasferì in Olanda, e iniziò il suo primo libro, Le Monde, ou Traité de la lumière, sulla fisica della luce. La pubblicazione fu ritardata perché, quando venne a sapere degli arresti domiciliari di Galileo Galilei, Descartes si fece molto più cauto. Il libro fu pubblicato, in una forma incompleta, dopo la sua morte. Sviluppò invece le sue idee sul pensiero logico in un importante lavoro pubblicato nel 1637: il Discours de la méthode. Il libro aveva tre appendici: La Dioptrique, Les Météores e La Géométrie.
Il suo libro più ambizioso, i Principia Philosophiae, fu pubblicato nel 1644. Era diviso in quattro parti: Principi della conoscenza umana, Principi delle cose materiali, Il mondo visibile e La terra. Si presentava come un tentativo di fornire un fondamento matematico unificato all’intero universo fisico, riducendo alla meccanica tutto quanto vi è in natura.
Nel 1649, Descartes si trasferì in Svezia, come precettore della regina Cristina. La regina era mattiniera, mentre Descartes era solito alzarsi verso le 11. Le lezioni di matematica impartite alla regina tutte le mattine alle 5, in un clima rigido, diedero un duro colpo alla salute di Descartes. Dopo pochi mesi, morì di polmonite.
Le coordinate come sono usate oggi
La formulazione iniziale della geometria delle coordinate sarà più chiara se prima spieghiamo come funziona la versione moderna. Esistono diverse varianti, ma la più comune si ha tracciando nel piano due rette perpendicolari tra loro, dette assi, il cui punto di incontro si chiama origine. Per convenzione si assume che gli assi siano uno orizzontale e l’altro verticale.
Lungo i due assi scriviamo i numeri interi, con i numeri negativi che vanno in una direzione e i positivi nell’altra. Tradizionalmente, l’asse orizzontale si chiama asse x, quello verticale asse y. I simboli x e y sono usati per rappresentare punti su quei rispettivi assi, cioè distanze dall’origine. Un punto generico nel piano, con una distanza x lungo l’asse orizzontale e una distanza y lungo l’asse verticale, è individuato da una coppia di numeri (x, y). Questi numeri rappresentano le coordinate del punto.
Un’equazione che contiene x e y limita i punti possibili a quelli le cui coordinate soddisfano l’equazione. Per esempio, se x2 + y2 = 1 allora (x, y) deve trovarsi a distanza 1 dall’origine, per il teorema di Pitagora. Tali punti formano una circonferenza, centrata nell’origine, di raggio 1. Diciamo che x2 + y2 = 1 è l’equazione di quella circonferenza. Ogni equazione corrisponde a una curva nel piano; viceversa ogni curva corrisponde a un’equazione.
Per esempio, su una mappa, x può essere la distanza a est dall’origine (con i numeri negativi che rappresentano le distanze verso ovest), mentre y può essere la distanza a nord dall’origine (con i numeri negativi che rappresentano le distanze verso sud).
Le coordinate funzionano anche nello spazio tridimensionale; ora però per individuare un punto non sono sufficienti due numeri, ma tre numeri sì. Oltre alle distanze est-ovest e nord-sud dobbiamo conoscere la distanza del punto sopra o sotto l’origine. In genere si usa un numero positivo per le distanze al di sopra, e un numero negativo per le distanze al di sotto. Le coordinate nello spazio hanno la forma (x, y, z).
Questo è il motivo per cui il piano si dice bidimensionale, mentre lo spazio è tridimensionale. Il numero di dimensioni corrisponde al numero di valori necessari per specificare un punto.
Nello spazio tridimensionale, un’unica equazione contenente x, y e z definisce in genere una superficie. Per esempio, x2 + y2 + z2 = 1 asserisce che il punto (x, y, z) è sempre alla distanza di una unità dall’origine, e questo implica che si trovi sulla sfera unitaria con centro nell’origine.
Si noti che il termine «dimensione» in questo caso non è affatto definito nel significato che gli è proprio. Non troviamo il numero di dimensioni di uno spazio trovando cose chiamate dimensioni e poi contandole. Calcoliamo invece quanti numeri sono necessari per specificare dove si trova una posizione nello spazio, e quello è il numero di dimensioni.
Coordinate cartesiane
La geometria delle coordinate cartesiane rivela un’unità algebrica dietro le sezioni coniche, curve che i greci avevano costruito come sezioni di un doppio cono. In termini algebrici, si ha che le sezioni coniche sono le curve più semplici dopo le rette. Una retta corrisponde a un’equazione lineare
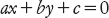
con a, b, c costanti. Una sezione conica corrisponde a un’equazione quadratica

con a, b, c, d, e, f costanti. Descartes affermò questo fatto, ma non fornì alcuna dimostrazione. Ad ogni modo, studiò un caso speciale, basato su un teorema dovuto a Pappo che caratterizzava le sezioni coniche, e dimostrò che in questo caso l’equazione risultante è quadratica.
Proseguì a considerare equazioni di grado maggiore, definendo curve più complesse della maggior parte di quelle che si presentano nella geometria greca classica. Un esempio tipico è il folium di Descartes, con equazione

che forma un anello con due estremi che tendono all’infinito.
Il contributo forse più importante derivato dal concetto di coordinate compare a questo punto: Descartes si distaccò dalla concezione greca delle curve come cose che sono costruite con significati geometrici precisi, e le vide come rappresentazione visiva delle formule algebriche. Come sottolineò Newton nel 1707, «i moderni andando molto oltre [rispetto ai greci] hanno incluso nella geometria tutte le curve che possono essere espresse da equazioni».

Figura 6.3
Il folium di Descartes.
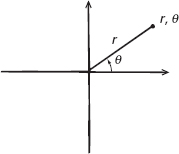
Figura 6.4
Coordinate polari.
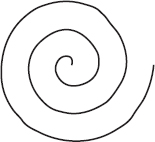
Figura 6.5
La spirale di Archimede.
Quale Bernoulli fece cosa? Prontuario sui Bernoulli
La famiglia svizzera dei Bernoulli ebbe un’enorme influenza sullo sviluppo della matematica. Nell’arco di quattro generazioni i Bernoulli produssero grandi risultati in matematica, sia pura che applicata. Spesso descritta come una mafia matematica, i Bernoulli in genere mossero i primi passi in settori come la legge, la medicina o la chiesa, ma alla fine cambiarono strada e diventarono matematici, professionisti o dilettanti.
Molti concetti matematici diversi portano il nome di Bernoulli. Non si tratta sempre dello stesso Bernoulli. Piuttosto che fornire dettagli biografici sui componenti della famiglia, presento un riassunto di chi fece cosa.
Jacob I (1654-1705)
Coordinate polari, formula per il raggio di curvatura di una curva piana. Curve speciali, come la catenaria e la lemniscata. Dimostrò che un’isocrona (una curva lungo la quale un corpo cade con velocità verticale uniforme) è una cicloide invertita. Discusse le figure isoperimetriche, che hanno lunghezza minima sotto determinate condizioni, un argomento che in seguito portò al calcolo delle variazioni. Tra i primi studiosi di probabilità, e autore del primo libro sull’argomento, Ars Conjectandi. Chiese che sulla sua pietra tombale fosse incisa una spirale logaritmica, accompagnata dall’iscrizione Eadem mutata resurgo (risorgo uguale eppure diversa).
Johann I (1667-1748)
Sviluppò l’analisi infinitesimale e la divulgò in Europa. Un suo allievo, il marchese de l’Hôpital, incluse il lavoro di Johann nel suo primo trattato di analisi infinitesimale. La regola di l’Hôpital per il calcolo dei limiti che si riducono a 0/0 si deve a Johann. Nei suoi scritti trattò l’ottica (riflessione e rifrazione), le traiettorie ortogonali di famiglie di curve, le lunghezze delle curve e la valutazione di aree con serie, la trigonometria analitica e la funzione esponenziale. Brachistocrona (curva che permette di scendere nel minor tempo possibile), lunghezza della cicloide.
Nicolaus I (1687-1759)
Coprì la cattedra di matematica che era stata di Galileo a Padova. Scrisse di geometria ed equazioni differenziali. In seguito, insegnò logica e legge. Matematico dotato ma non molto produttivo. Intrattenne una corrispondenza con Leibniz, Eulero e altri; i suoi maggiori successi sono sparsi in circa 560 lettere. Formulò il paradosso di San Pietroburgo in probabilità.
Criticò l’uso indiscriminato da parte di Eulero delle serie divergenti. Collaborò alla pubblicazione dell’Ars Conjectandi di Jacob Bernoulli. Sostenne Leibniz nella sua controversia con Newton.
Nicolaus II (1695-1726)
Chiamato all’Accademia di San Pietroburgo, morì per annegamento otto mesi dopo. Discusse il paradosso di San Pietroburgo con Daniel.
Daniel (1700-1782)
Il più noto dei tre figli di Johann. Studiò probabilità, astronomia, fisica e idrodinamica. Il suo trattato del 1738, Hydrodynamica, contiene il principio di Bernoulli sulla relazione tra pressione e velocità. Scrisse sulle maree, la teoria cinetica dei gas e le corde vibranti. Pioniere nelle equazioni differenziali parziali.
Johann II (1710-1790)
Il più giovane dei tre figli di Johann. Studiò legge ma divenne professore di matematica a Basilea. Studiò la teoria matematica del calore e della luce.
Johann III (1744-1807)
Come suo padre, studiò legge, ma si dedicò poi alla matematica. Chiamato all’Accademia di Berlino all’età di 19 anni. Scrisse di astronomia, probabilità e decimali ricorrenti.
Jacob II (1759-1789)
Importanti lavori sull’elasticità, l’idrostatica e la balistica.
Gli studiosi successivi inventarono numerose variazioni sul sistema di coordinate cartesiano. In una lettera del 1643, Fermat riprese le idee di Descartes e le estese a tre dimensioni. Qui egli faceva riferimento a superfici come ellissoidi e paraboloidi, che sono definiti da equazioni quadratiche nelle tre variabili x, y e z. Un contributo influente fu l’introduzione di coordinate polari a opera di Jacob Bernoulli nel 1691. Per individuare i punti nel piano, questi usò un angolo θ e una distanza r invece di una coppia di assi. In questo caso, le coordinate sono (r, θ).
Di nuovo, le equazioni espresse in queste variabili rappresentano curve. Ma ora, equazioni semplici possono rappresentare curve che sarebbero molto complicate in coordinate cartesiane. Per esempio, l’equazione r = θ corrisponde a una spirale, del tipo noto come spirale di Archimede.
Funzioni
Un’importante applicazione delle coordinate in matematica è un metodo per rappresentare graficamente le funzioni.
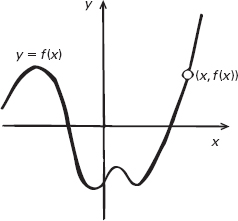
Figura 6.6
Il grafico di una funzione f.
Una funzione non è un numero, ma una ricetta che a partire da un certo numero calcola un numero associato. La ricetta in questione è spesso enunciata come una formula, che assegna a ogni numero, x (possibilmente in un intervallo limitato), un altro numero, f(x).
Per esempio, la funzione radice quadrata è
definita dalla regola 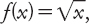 che indica infatti di
estrarre la radice quadrata del numero dato. Questa ricetta
richiede che il valore di x sia positivo. In maniera
analoga, la funzione quadrato è definita da f(x)
= x2, e questa volta non abbiamo vincoli su
x.
che indica infatti di
estrarre la radice quadrata del numero dato. Questa ricetta
richiede che il valore di x sia positivo. In maniera
analoga, la funzione quadrato è definita da f(x)
= x2, e questa volta non abbiamo vincoli su
x.
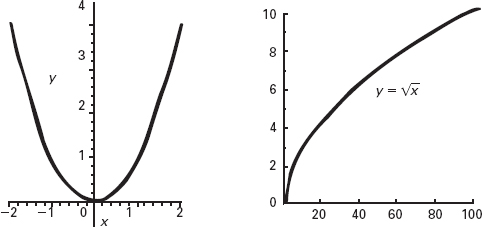
Figura 6.7
Grafici della funzione quadrato e della funzione radice quadrata.

Figura 6.8
Grafico della funzione seno.
Quello che le coordinate fecero per loro
La geometria delle coordinate può essere usata su superfici più complicate del piano, come la sfera. Le coordinate più usate sulla sfera sono la longitudine e la latitudine. La cartografia e l’uso delle mappe in navigazione si possono quindi considerare come applicazioni della geometria delle coordinate.
Il principale problema di navigazione per un comandante era la determinazione della latitudine e della longitudine della nave. La latitudine è relativamente semplice, perché l’angolo del Sole sopra l’orizzonte varia con la latitudine e può essere registrato in una tabella. Dal 1730, lo strumento standard per trovare la latitudine era il sestante (ora reso per lo più obsoleto dal GPS). Questo era stato inventato da Newton, il quale però non aveva pubblicato il risultato. Il sestante venne riscoperto in maniera indipendente dal matematico inglese John Hadley e dall’inventore americano Thomas Godfrey. In precedenza, i naviganti avevano usato l’astrolabio, che risale alla civiltà araba medievale.
La longitudine è più complessa. Il problema fu alla fine risolto per mezzo della costruzione di un orologio molto accurato, che era regolato sull’ora locale all’inizio del viaggio. L’ora dell’alba e del tramonto, e il movimento della Luna e delle stelle, dipendono dalla longitudine, e rendono possibile determinarne il valore confrontando l’ora locale con quella indicata dall’orologio. La storia dell’invenzione del cronometro a opera di John Harrison, che risolse il problema, è raccontata nel famoso libro di Dava Sobel Longitudine.
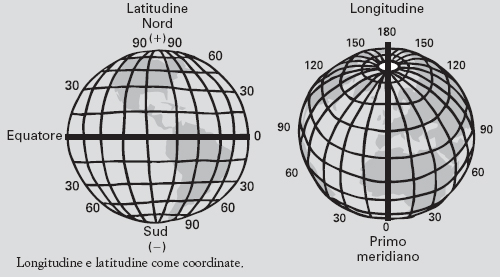
Longitudine e latitudine come coordinate.
Possiamo rappresentare una funzione in termini geometrici definendo la coordinata y, per un determinato valore di x, con y = f(x). Questa equazione stabilisce una relazione tra le due coordinate, e determina quindi una curva, che è detta grafico della funzione f.
Il grafico della funzione f(x)
= x2 è una parabola; quello della radice
quadrata 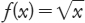 è metà di una parabola, ma
adagiata sul fianco. Funzioni più complicate portano a curve più
complicate. Il grafico della funzione seno y =
senx è una curva ondulata.
è metà di una parabola, ma
adagiata sul fianco. Funzioni più complicate portano a curve più
complicate. Il grafico della funzione seno y =
senx è una curva ondulata.
Quello che le coordinate fanno per noi
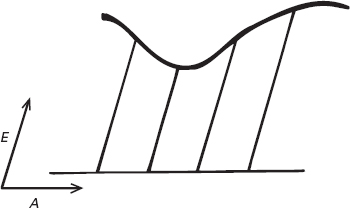
Noi continuiamo a usare le coordinate per le mappe, ma un altro uso comune della geometria delle coordinate si ha nel mercato azionario, dove le fluttuazioni di un prezzo sono registrate come una curva. In questo caso la coordinata x rappresenta il tempo, mentre la coordinata y è il prezzo. Enormi quantità di dati economici e scientifici sono registrati nella stessa maniera.
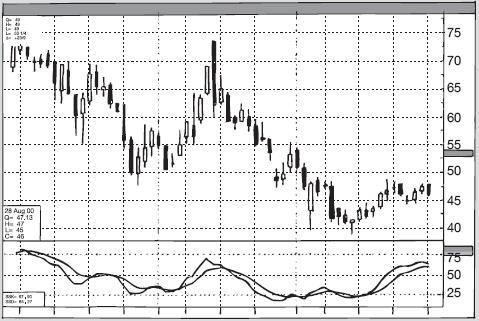
Fluttuazioni del mercato azionario rappresentate in termini di coordinate.
La geometria delle coordinate oggi
Le coordinate sono una di quelle idee semplici che hanno avuto una pesante influenza sulla vita quotidiana. Noi le usiamo ovunque, e in genere non ce ne accorgiamo neppure. Di fatto, tutta la grafica dei computer impiega un sistema di coordinate interno, e la geometria che compare sullo schermo è trattata in termini algebrici. Un’operazione tanto semplice come ruotare di pochi gradi una fotografia digitale, per mettere in orizzontale l’orizzonte, fa affidamento sulla geometria delle coordinate.
Il messaggio principale della geometria delle coordinate riguarda le connessioni incrociate in matematica. Concetti la cui realizzazione fisica sembra totalmente diversa possono rivelarsi come aspetti differenti della stessa cosa. L’apparenza può essere fuorviante. Buona parte dell’efficacia della matematica come strumento per comprendere l’universo deriva dalla sua capacità di adattare idee, e trasferirle da un’area della scienza a un’altra. La matematica è il massimo se si tratta di trasferire tecnologia. Ed è questa connessione incrociata, rivelata a noi negli ultimi 4000 anni, che rende la matematica una materia unica e unificata.