4.
Le lusinghe dell’ignoto
La x indica il tesoro
In matematica, i simboli non sono usati soltanto per rappresentare i numeri, come si capisce subito sfogliando qualunque testo sull’argomento. Il primo passo importante verso il ragionamento simbolico, diverso dalla pura rappresentazione simbolica, fu fatto nell’ambito del problem solving, cioè l’insieme delle attività finalizzate alla risoluzione di un problema. Numerosi testi antichi, che risalgono al periodo antico-babilonese, presentano ai lettori alcuni dati su una certa quantità ignota, e poi chiedono di trovarne il valore. Una comune formula (in senso letterale) trovata sulle tavolette babilonesi suona come: «Ho trovato una pietra ma non l’ho pesata». Dopo alcune informazioni supplementari («quando ho aggiunto una seconda pietra pesante la metà, il peso totale era 15 gin») allo studente si richiede di calcolare il peso della prima pietra.
Algebra
Problemi di questo tipo diedero in seguito origine a quella che ora chiamiamo algebra, dove i numeri sono rappresentati da lettere. La quantità incognita è per tradizione indicata con la lettera x, le condizioni che si applicano a x sono enunciate come varie formule matematiche, e allo studente si insegnano metodi standard per derivare il valore di x da quelle formule. Per esempio, il problema babilonese esposto sopra si potrebbe scrivere come x + 1/2 x = 15, e impareremmo come ricavare che x = 10.
A livello scolastico, l’algebra è una branca della matematica in cui i numeri incogniti sono rappresentati da lettere, le operazioni dell’aritmetica sono rappresentate da simboli e lo scopo principale è ricavare da alcune equazioni i valori delle quantità incognite. Un problema tipico dell’algebra scolastica è trovare un numero incognito x, data l’equazione x2 + 2x = 120. Questa equazione quadratica ha una sola soluzione positiva, x = 10. In questo caso x2 + 2x = 102 + 2 × 10 = 100 + 20 = 120. L’equazione ha anche una soluzione negativa, x = −12. Con questo valore, x2 + 2x = (−12)2 + 2 × (−12) = 144 − 24 = 120. Gli antichi avrebbero accettato la soluzione positiva, ma non quella negativa. Oggi noi le ammettiamo entrambe, perché in molti problemi i numeri negativi hanno un significato sensato e corrispondono a risposte fisiche possibili, e perché la matematica di fatto diventa più semplice se si permettono i numeri negativi.
Nella matematica avanzata, l’uso di lettere al posto di numeri è soltanto un piccolo aspetto dell’algebra, il contesto in cui ebbe inizio. L’algebra si occupa delle proprietà di espressioni simboliche in quanto tali: riguarda la struttura e la forma, non semplicemente il numero. Questa visione più generale dell’algebra si sviluppò quando i matematici cominciarono a porsi domande generali sull’algebra di livello scolastico. Invece di tentare di risolvere equazioni specifiche, si concentrarono sulla struttura più profonda del processo di soluzione in sé.
Come nacque l’algebra? Dapprima vennero i problemi e i metodi di risoluzione. Soltanto in seguito fu inventata la notazione simbolica, quella che noi ora riteniamo sia l’aspetto centrale della questione. Esistevano diversi sistemi di notazione, ma alla fine uno soltanto sbaragliò tutti gli altri. Il termine «algebra» comparve a metà di questo processo, ed è di origine araba. (Il suffisso iniziale «al», l’articolo arabo, ne indica la provenienza).
Equazioni
Quella che ora per noi è la soluzione di un’equazione, in cui una quantità incognita deve essere ricavata a partire da una opportuna informazione, è antica quasi quanto l’aritmetica. Esiste una testimonianza indiretta del fatto che i babilonesi risolvessero equazioni abbastanza complicate già nel 2000 a. C., e una prova diretta per soluzioni di problemi più semplici, descritti su tavolette cuneiformi, che risalgono al 1700 a. C. circa.
La porzione che rimane della Tavoletta YBC 4652, risalente al periodo antico-babilonese (1800-1600 a. C.), contiene undici problemi da risolvere; il testo sulla tavoletta indica che in origine i problemi erano 22. Una questione tipica è:
«Ho trovato una pietra, ma non l’ho pesata. Dopo che ho pesato sei volte il suo peso, ho aggiunto 2 gin e ho aggiunto un terzo di un settimo moltiplicato per 24, l’ho pesata. Il risultato è stato 1 ma-na. Qual era il peso originario della pietra?»
Un peso di 1 ma-na equivale a 60 gin.
Nella notazione moderna, indicheremmo con x il peso richiesto in gin. Il problema ci dice che
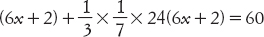
e i metodi algebrici tradizionali permettono di ottenere la risposta x = 4⅓ gin. La tavoletta riporta questa soluzione ma non fornisce alcuna chiara indicazione di come ottenerla. Possiamo essere sicuri che non sia stata ricavata con metodi simbolici simili a quelli che usiamo noi ora, perché tavolette di epoca successiva descrivono metodi di soluzione in termini di esempi tipici, come «dimezza questo numero, somma il prodotto di questi due, calcola la radice quadrata…» e così via.
Questo problema, insieme agli altri che compaiono sulla tavoletta YBC 4652, rappresenta quella che noi ora chiamiamo equazione lineare, in quanto l’incognita x compare soltanto alla prima potenza. Tutte le equazioni di questo tipo possono essere riscritte nella forma
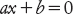
con soluzione x = −b/a. Nei tempi antichi però, quando non esisteva il concetto di numero negativo e neppure la manipolazione simbolica, trovare una soluzione non era così semplice. Anche oggi, molti studenti avrebbero qualche difficoltà con il problema esposto sulla tavoletta YBC 4652.
Più interessanti sono le equazioni quadratiche, in cui l’incognita può anche comparire elevata alla seconda potenza, cioè al quadrato. L’espressione moderna ha la forma
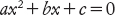
ed esiste una formula standard per ricavare il valore di x. Il metodo dei babilonesi è illustrato da un problema decifrato sulla tavoletta BM 13901:
«Ho sommato sette volte il lato del mio quadrato e undici volte l’area, [ottenendo] 6;15».
(Qui 6;15 è la forma semplificata della notazione
sessagesimale babilonese, e significa 6 più 15/60, cioè 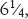 nella notazione moderna). La soluzione riportata dice:
nella notazione moderna). La soluzione riportata dice:
«Scrivi 7 e 11. Moltiplichi 6;15 per 11, [ottenendo] 1,8;45. Calcoli la metà di 7, [ottenendo] 3;30 e 3;30. Moltiplichi, [ottenendo] 12;15. Sommi [questo] a 1,8;45 [ottenendo] come risultato 1,21. Questo è il quadrato di 9. Sottrai 3;30, che moltiplichi, da 9. Si ottiene 5;30. Il reciproco di 11 non si può trovare. Per che cosa devo moltiplicare 11 per ottenere 5;30? [La risposta è] 0;30, il lato del quadrato è 0;30».
Si noti che la tavoletta dice al lettore che cosa fare, ma non perché. È una ricetta. Qualcuno deve aver compreso perché funzionava, in modo da descriverla la prima volta, ma una volta scoperta poteva poi essere usata da chiunque fosse opportunamente istruito. Non sappiamo se le scuole babilonesi insegnassero semplicemente la ricetta, o spiegassero perché funzionava.
La ricetta, per com’è enunciata, suona misteriosa, ma è più semplice da interpretare rispetto a quanto potremmo credere. I numeri complicati di fatto aiutano: rendono più chiare le regole usate. Per trovarle, dobbiamo semplicemente essere sistematici. Nella notazione moderna scriviamo:
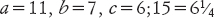
Allora l’equazione prende la forma
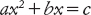
con quei particolari valori per a, b, c. Dobbiamo ricavare x. La soluzione babilonese ci dice di:
(1) moltiplicare c per a, per ottenere ac;
(2) dividere b per 2, per ottenere b/2;
(3) elevare al quadrato b/2, per ottenere b2/4;
(4) sommare questo valore ad ac, per ottenere ac + b2/4;
(5) estrarre la radice quadrata 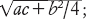
(6) sottrarre b/2,
per ottenere 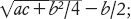
(7) dividere questo valore per a, per ottenere la soluzione
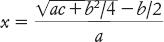
Questo procedimento equivale alla formula

insegnata oggi perché nell’equazione scriviamo il temine c a sinistra, dove diventa −c.
È abbastanza chiaro che i babilonesi sapevano che il loro procedimento era generale. L’esempio citato è troppo complesso perché la soluzione sia di tipo speciale, concepito per adattarsi a quel problema soltanto.
Come arrivarono i babilonesi al loro metodo, e in che modo lo consideravano? Doveva esserci un’idea abbastanza semplice sotto un procedimento così complicato. Sembra plausibile, anche se non ne abbiamo testimonianza diretta, che avessero un’idea geometrica, quella di completare il quadrato. Una versione algebrica di questo problema è insegnata anche oggi. Possiamo rappresentare il problema, che per chiarezza scegliamo di scrivere nella forma x2 + ax = b, con un’illustrazione:
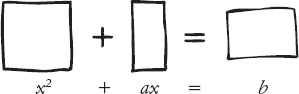
In questo caso, il quadrato e il primo rettangolo hanno altezza x; le loro larghezze sono rispettivamente x e a. Il rettangolo più piccolo ha area b. La ricetta babilonese in realtà scompone il primo rettangolo in due porzioni,
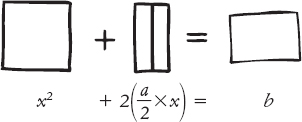
Possiamo quindi disporre diversamente le due nuove porzioni di rettangolo e affiancarle ai lati del quadrato:
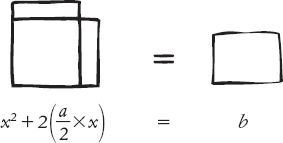
Il disegno a sinistra aspetta ora di essere completato per diventare un quadrato più grande, aggiungendo il quadratino ombreggiato:
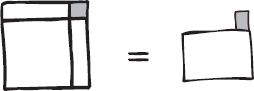
Per mantenere valida l’equazione, aggiungiamo lo stesso quadratino ombreggiato anche all’altro disegno. Ora però riconosciamo che il disegno a sinistra rappresenta il quadrato di lato (x + a/2), e la rappresentazione geometrica è equivalente all’enunciato algebrico
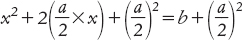
Dal momento che il membro a sinistra è un quadrato, possiamo riscriverlo come
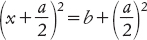
e a questo punto è naturale calcolare una radice quadrata
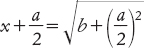
e finalmente riscrivere l’espressione per dedurre che
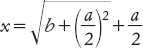
e questa è esattamente la procedura seguita dalla ricetta babilonese.
Non abbiamo alcuna testimonianza su tavoletta a sostegno dell’idea che questa costruzione geometrica abbia condotto i babilonesi alla loro ricetta. Ad ogni modo, questa ipotesi è plausibile, ed è supportata in via indiretta da diversi disegni rinvenuti su tavolette di argilla.
«Al-jabr»
Il termine «algebra» deriva dall’arabo al-jabr, un’espressione usata da Muhammad ibn Mūsā al-Khwārizmī, che visse intorno all’anno 820. La sua opera al-Kitāb al-mukhtasar fī hisāb al-jabr wa al-muqābala spiega metodi generali per risolvere equazioni manipolando quantità incognite.
Al-Khwārizmī usa parole, non simboli, ma i suoi metodi sono chiaramente simili a quelli insegnati oggi. Al-jabr significa «sommare quantità uguali da entrambe le parti di un’equazione», che è quanto facciamo quando partiamo da
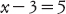
per ricavare
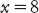
In realtà, giungiamo a questo risultato sommando 3 da entrambe le parti. Al-muqābala ha due significati. Ha un significato speciale: «sottrarre uguali quantità da entrambe le parti di un’equazione», che applichiamo per passare da
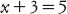
alla soluzione
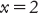
ma ha anche il significato generale di «confronto».
Al-Khwārizmī fornisce regole generali per risolvere sei tipi di equazioni, che combinate possono essere applicate per risolvere tutte le equazioni lineari e quadratiche. Nella sua opera, poi, troviamo le idee dell’algebra elementare, ma non l’uso di simboli.
Equazioni cubiche
I babilonesi erano in grado di risolvere le equazioni quadratiche, e di fatto il loro metodo era simile a quello insegnato oggi. In termini algebrici, non richiede nulla di più complicato di una radice quadrata, oltre le operazioni elementari dell’aritmetica (addizione, sottrazione, moltiplicazione, divisione). Il naturale passo successivo è rappresentato dalle equazioni cubiche, che contengono il cubo dell’incognita. Scriviamo le equazioni di questo tipo come
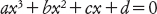
dove x rappresenta l’incognita e i coefficienti a, b, c, d sono numeri noti. Prima di ammettere i numeri negativi però, i matematici classificavano le equazioni cubiche in molti tipi differenti, e dunque, per esempio, x3 + 3x = 7 e x3 − 3x = 7 erano considerate equazioni completamente diverse, e richiedevano metodi diversi di soluzione.
I greci avevano scoperto come usare le sezioni coniche per risolvere alcune equazioni cubiche. L’algebra moderna mostra che se una conica interseca un’altra conica, i punti di intersezione sono determinati da un’equazione di terzo o quarto grado (dipende dalla conica). I greci non conoscevano il risultato generale, ma ne sfruttavano le conseguenze in casi particolari, e usavano le coniche come un nuovo tipo di strumento geometrico.
Questo metodo di soluzione fu perfezionato e formalizzato dal persiano Omar Khayyām, più noto per la sua opera in quartine Rubaiyat. Intorno al 1075, nel suo trattato Sulle dimostrazioni dei problemi di al-jabr e al-muqabalah, Khayyām catalogò le equazioni cubiche in quattordici tipi, e mostrò come giungere in ogni caso alla soluzione usando le coniche. Il trattato si presentava come un tour de force di geometria, e affrontava in maniera quasi completa il problema geometrico. Un matematico moderno solleverebbe qualche obiezione: alcuni dei casi di Omar non sono completamente risolti perché egli si basa sull’ipotesi che certi punti costruiti geometricamente esistano, quando talvolta non è così. Questo significa che Omar assume che le sue coniche si incontrino, quando magari non lo fanno, ma questi sono peccati veniali.
Le soluzioni geometriche delle equazioni cubiche andavano benissimo, ma potevano esistere soluzioni algebriche, che non implicassero oggetti matematici più complicati delle radici cubiche? I matematici italiani del Rinascimento compirono uno dei maggiori progressi in algebra quando scoprirono che la risposta era affermativa.
A quei tempi, i matematici costruivano la propria fama partecipando a particolari gare pubbliche di abilità matematica, i «cartelli di matematica disfida». Ognuno dei contendenti sottoponeva all’avversario i propri quesiti, e chi riusciva a risolverne il maggior numero era dichiarato vincitore. Il pubblico poteva scommettere sul vincitore e anche i contendenti scommettevano spesso ingenti somme di denaro (in un caso di cui abbiamo testimonianza, lo sconfitto dovette offrire al vincitore, e ai suoi amici, trenta banchetti). Il vincitore aveva inoltre una maggiore probabilità di attrarre discepoli a pagamento, soprattutto di nobile estrazione. I «duelli» matematici pubblici erano davvero una cosa seria.
Nel 1535 si tenne proprio una di queste disfide, tra Antonio Maria Fior e Niccolò Fontana, soprannominato Tartaglia, per l’evidente difficoltà ad articolare le parole. Tartaglia sbaragliò completamente Fior, e la notizia della vittoria si diffuse, fino a giungere alle orecchie di Girolamo Cardano, che si fecero attente. Questi stava scrivendo un trattato di matematica, e i problemi con i quali Fior e Tartaglia si erano sfidati erano… equazioni cubiche. A quei tempi, le equazioni cubiche erano classificate in tre tipi distinti, sempre perché i numeri negativi non erano ammessi. Fior sapeva soltanto come risolvere le equazioni cubiche di un tipo. Al principio, Tartaglia sapeva soltanto come risolvere le equazioni di un tipo diverso. Nella simbologia moderna, la sua soluzione di un’equazione cubica del tipo x3 + ax = b è

In un lampo di genio ispirato dalla disperazione, circa una settimana prima della disfida Tartaglia scoprì come risolvere anche gli altri tipi di equazioni, e sapendo quali erano le equazioni che Fior non sapeva risolvere, sottopose all’avversario proprio problemi di quel tipo.
Cardano, venuto a conoscenza della disfida, comprese che i due matematici avevano concepito metodi per risolvere le equazioni cubiche. Con l’intenzione di trattare questi argomenti nel suo libro, avvicinò Tartaglia e gli chiese di spiegargli i suoi metodi. Tartaglia si mostrò naturalmente restio, perché quelle tecniche rappresentavano la sua fonte di sostentamento, ma alla fine fu convinto a rivelare il segreto. Secondo Tartaglia, Cardano promise di non rivelare mai il metodo. È quindi comprensibile che Tartaglia si sia risentito quando la sua scoperta apparve nell’Ars magna di Cardano, il grande trattato sull’algebra. Tartaglia reclamò a gran voce e accusò Cardano di plagio.
A dire il vero, Cardano non era proprio un puro. Era un incallito giocatore d’azzardo, che aveva vinto e perso notevoli somme di denaro a carte, ai dadi e anche a scacchi. Aveva dilapidato in questo modo tutte le fortune di famiglia, ed era ridotto in povertà. Era anche un genio, un valido medico, un brillante matematico e un abile promotore di se stesso, per quanto le sue qualità positive fossero ridimensionate dalla schiettezza che spesso si trasformava in un modo di fare brusco e offensivo. Possiamo quindi perdonare Tartaglia per aver supposto che Cardano gli avesse mentito con lo scopo di rubargli la scoperta. Il fatto che Cardano nel suo libro riconosca la paternità a Tartaglia non fece che peggiorare le cose: Tartaglia sapeva che sarebbe passato alla storia il nome dell’autore del libro, e non qualche ignoto personaggio citato in un punto.
Serie di Fibonacci
La terza parte del Liber abaci contiene un problema che sembra risalire a Leonardo: «Un tale mise una coppia di conigli in un luogo completamente circondato da pareti. Quante coppie di conigli possono discendere da quella coppia in un anno se ogni mese ogni coppia genera una nuova coppia, che dal secondo mese di vita comincia a procreare?»
Questo problema piuttosto bizzarro conduce a una strana, e famosa, successione di numeri:

e così via. Ogni numero è la somma dei due che lo precedono. Questa successione è nota come «serie di Fibonacci», e si presenta più volte sia in matematica che in natura. In particolare, il numero dei petali di molti fiori compare nella serie. Non si tratta di una coincidenza, ma è una conseguenza del modello di crescita della pianta e della geometria dei «primordi», piccoli insiemi di cellule all’apice del germoglio che danno origine a importanti strutture, compresi i petali.
Anche se la regola di Fibonacci per la crescita della popolazione di conigli è poco realistica, andamenti più generali di questo tipo (i modelli di Leslie) sono usati oggi per certi problemi di dinamica delle popolazioni, cioè lo studio dell’andamento delle popolazioni di animali in seguito alla nascita e alla morte dei singoli individui.
Ad ogni modo, Cardano aveva una scusa, assolutamente valida, e aveva anche una buona ragione per non mantenere la sua promessa a Tartaglia. La ragione era che un allievo di Cardano, Ludovico Ferrari, aveva trovato un metodo per risolvere le equazioni quartiche, nelle quali compare la quarta potenza dell’incognita. Questo fatto era completamente nuovo e di estrema importanza. Cardano naturalmente voleva trattare nel suo libro anche le equazioni quartiche. Dal momento che era stato un suo allievo a fare la scoperta, questo era assolutamente legittimo. Il metodo di Ferrari però riduceva la soluzione di qualunque quartica a quella di una cubica associata, e dunque faceva affidamento alla soluzione di Tartaglia per le equazioni cubiche. Cardano non poteva pubblicare il lavoro di Ferrari senza svelare anche quello di Tartaglia.
Quello che l’aritmetica fece per loro
Diversi capitoli del Liber abaci contengono problemi geometrici importanti per questioni commerciali. Uno, che non ha un’utilità pratica particolare, è così esposto: «Un uomo compra 30 uccelli: pernici, colombi e passeri. Una pernice costa 3 monete d’argento, un colombo 2 e un passero 1/2. L’uomo paga 30 monete d’argento. Quanti uccelli di ogni tipo compra?»
Nella notazione moderna, se indichiamo con x il numero di pernici, con y il numero di colombi, e con z il numero di passeri, dobbiamo risolvere le due equazioni
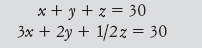
Considerando i numeri reali o razionali, queste equazioni avrebbero un numero infinito di soluzioni, ma il problema implica una condizione aggiuntiva, i numeri x, y e z devono essere interi. Di conseguenza esiste soltanto una soluzione: 3 pernici, 5 colombi e 22 passeri.
Leonardo cita anche una serie di problemi relativi all’acquisto di un cavallo. Un uomo dice all’altro: «Se mi dai un terzo del tuo denaro, io posso comprare il cavallo». L’altro gli risponde: «Se tu dai a me un quarto del tuo denaro, io posso comprare il cavallo». Quanto costa il cavallo? Questa volta esistono più soluzioni: la più piccola in numeri interi prevede che il cavallo costi 11 monete d’argento.
Girolamo Cardano (1501-1576)
Girolamo Cardano era figlio illegittimo del notaio milanese Fazio Cardano e della giovane vedova Clara Micheria. La donna aveva già tre figli, i quali morirono di peste a Milano mentre lei dava alla luce Girolamo nella vicina Pavia. Fazio era un abile matematico, e aveva trasmesso a Girolamo la sua passione per la materia. Contro il volere del padre, Girolamo studiò medicina all’Università di Pavia; Fazio avrebbe voluto che studiasse legge.
Ancora studente, Cardano fu eletto rettore dell’Università di Padova, dove si era trasferito, per un unico voto. Dopo aver speso la piccola eredità ricevuta dal padre morto da poco, per migliorare le proprie finanze Cardano cominciò a giocare d’azzardo: carte, dadi e scacchi. Portava sempre con sé un coltello, e una volta ferì al volto un avversario, convinto che quello barasse.
Nel 1525, Cardano divenne dottore in medicina, ma la sua domanda di far parte del Collegio dei medici praticanti di Milano venne respinta, forse per la sua cattiva reputazione. Esercitò la professione di medico a Sacco, e sposò Lucia Bandarini, figlia del capitano della milizia locale. Come medico non ebbe successo, e nel 1533 Girolamo ritornò al gioco d’azzardo, ma le cose andarono talmente male che fu costretto a dare in pegno le gioie della moglie e alcuni arredi di famiglia.
Cardano ebbe però un colpo di fortuna, poiché gli fu offerta la cattedra di matematica che era stata del padre alla Fondazione Piatti di Milano. Continuò anche a esercitare la medicina, poiché alcune cure miracolose valsero a far crescere la sua reputazione come medico. Nel 1539, dopo diversi tentativi, fu finalmente ammesso al Collegio dei medici e iniziò a scrivere testi di studio su vari argomenti, compresa la matematica. Scrisse anche un’importante autobiografia, il De vita propria, una raccolta di capitoli su vari argomenti. La sua carriera era al culmine, quando si recò a Edimburgo per curare l’arcivescovo di Sant’Andrea, John Hamilton, che soffriva di una grave forma d’asma. Con le cure di Cardano, la salute di Hamilton migliorò notevolmente, e Cardano lasciò la Scozia con 2000 corone d’oro in più. Divenne professore all’Università di Pavia, e le cose andarono bene fino a quando il figlio primogenito Giambattista, all’insaputa del padre, sposò Brandonia de’ Seroni, «una donna sfrontata e di nessun valore», a parere di Cardano. Lei e la sua famiglia schernirono pubblicamente Giambattista, che la avvelenò. Nonostante tutti gli sforzi di Cardano, Giambattista fu giustiziato. Nel 1570, Cardano fu accusato di eresia, per aver elaborato l’oroscopo di Gesù. Fu imprigionato, poi rilasciato, ma bandito dagli incarichi universitari. Si trasferì a Roma, dove il Papa inaspettatamente gli concesse una pensione, e fu nominato membro del Collegio dei medici.
Pronosticò la data della propria morte, e a quanto si dice fece in modo di confermarla commettendo suicidio. Nonostante tante tragedie, rimase un ottimista fino alla fine.
Fu allora che gli giunse una notizia che gli offriva una via di scampo. Fior, che aveva perso nella disfida con Tartaglia, era un allievo di Scipione del Ferro. Cardano era venuto a sapere che del Ferro aveva risolto tutti i tre tipi di cubiche, e non soltanto quella che aveva comunicato a Fior. Si diceva inoltre che un certo Annibale della Nave fosse in possesso dei manoscritti non pubblicati di del Ferro. Cardano e Ferrari si recarono a Bologna nel 1543 per incontrare della Nave, consultarono le carte… e là, chiare come il sole, c’erano le soluzioni di tutti i tre tipi di cubiche. Cardano poteva in onestà dire di non aver pubblicato il metodo di Tartaglia, ma quello di del Ferro.
Tartaglia non la pensava allo stesso modo, ma non fu in grado di controbattere in maniera efficace a Cardano quando questi affermò che la soluzione non era affatto una scoperta di Tartaglia ma di del Ferro. Tartaglia pubblicò una lunga e dura diatriba sulla questione, e fu sfidato pubblicamente da Ferrari, in difesa del suo maestro. Ferrari vinse a mani basse, e Tartaglia non si riprese più dalla sconfitta.
Simbolismo algebrico
I matematici italiani del Rinascimento avevano sviluppato diversi metodi algebrici, ma usavano una notazione ancora rudimentale. Ci vollero centinaia di anni per lo sviluppo del simbolismo algebrico moderno.
Uno dei primi a usare simboli al posto di numeri incogniti fu Diofanto di Alessandria. La sua Arithmetica, scritta intorno al 250, consisteva in origine di 13 libri, sei dei quali sopravvissuti come copie successive. Il tema principale è la soluzione delle equazioni algebriche, in numeri interi o razionali, cioè frazioni p/q dove p e q sono numeri interi. La notazione di Diofanto è molto diversa da quella che usiamo oggi. Anche se l’Arithmetica è l’unico documento in merito giunto fino a noi, c’è una certa evidenza del fatto che Diofanto facesse parte di una corrente più ampia, e non fosse soltanto una figura isolata. La notazione di Diofanto non è molto adatta ai calcoli, ma li rappresenta in una forma compatta.
I matematici arabi del periodo medievale avevano sviluppato metodi sofisticati per la risoluzione di equazioni, ma le esprimevano in parole, non in simboli.
Il passaggio alla notazione simbolica ebbe un’accelerazione nel periodo rinascimentale. Il primo dei grandi algebristi a usare simboli fu François Viète, che enunciò molti dei suoi risultati in forma simbolica, con una notazione che comunque differisce molto da quella attuale. Questi usava comunque le lettere dell’alfabeto per rappresentare quantità note, e anche le incognite. Per distinguerle, stabilì che le consonanti B, C, D, F, G… rappresentassero quantità note, mentre le vocali A, E, I… rappresentassero le incognite.
Nel XV secolo, comparvero alcuni primi simboli, in particolare le lettere p e m per l’addizione e la sottrazione: plus e minus. Si trattava di abbreviazioni più che di simboli veri e propri. Anche i simboli + e − comparvero all’incirca in questo periodo, e in particolare in ambito commerciale, dove erano usati dai mercanti tedeschi per distinguere gli articoli sottopeso e quelli sovrappeso. Anche i matematici li adottarono presto, e il primo esempio scritto risale al 1481. William Oughtred introdusse il simbolo × per la moltiplicazione, e fu criticato apertamente (e a ragione) da Leibniz perché poteva essere confuso con la lettera x con estrema facilità.
La notazione di Diofanto e la nostra
| Significato | Simbolo moderno | Simbolo di Diofanto |
| L’incognita | x | γ |
| Il suo quadrato | x2 | Δγ |
| Il suo cubo | x3 | Kγ |
| La sua quarta potenza | x4 | ΔγΔ |
| La sua quinta potenza | x5 | ΔKγ |
| La sua sesta potenza | x6 | KγK |
| Addizione | + | Giustapposizione dei termini (AB per A + B) |
| Sottrazione | − |  |
| Eguaglianza | = | ισ |
Nel 1557, nel suo The Whetstone of
Witte, il matematico inglese Robert Recorde inventò il simbolo
= per l’eguaglianza, usato ancora oggi. Egli scrisse che non poteva
pensare a due cose più simili di due segmenti uguali paralleli. In
ogni caso, il simbolo usato da Recorde era molto più lungo rispetto
a quello che usiamo oggi, e assomigliava a  Viète
inizialmente aveva scritto la parola aequalis per indicare
l’eguaglianza, ma in seguito l’aveva sostituita con il simbolo ∼.
René Descartes usava un segno diverso,
Viète
inizialmente aveva scritto la parola aequalis per indicare
l’eguaglianza, ma in seguito l’aveva sostituita con il simbolo ∼.
René Descartes usava un segno diverso, 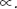
I simboli > e < usati oggi al posto di «maggiore di» e «minore di», sono dovuti a Thomas Harriot. Le parentesi rotonde ( ) comparvero nel 1544, mentre quelle quadrate [ ] e le graffe { } furono usate da Viète nel 1593 circa. Descartes usava il simbolo di radice quadrata √, che è un’elaborazione della lettera r di radice, ma scriveva √c per la radice cubica.
Per comprendere come la notazione algebrica rinascimentale fosse diversa dalla nostra, consideriamo un breve estratto dall’Ars magna di Cardano:

Nella notazione moderna scriveremmo
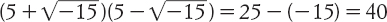
Qui dunque troviamo p: e m: per più e meno,
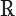 per «radice quadrata», e qd.
est per abbreviare l’espressione latina «il quale è». Cardano
scriveva
per «radice quadrata», e qd.
est per abbreviare l’espressione latina «il quale è». Cardano
scriveva
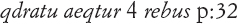
dove noi scriveremmo
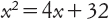
e quindi usava abbreviazioni diverse, rebus e qdratu, per l’incognita (la cosa) e il suo quadrato. Altrove usò R per l’incognita, Z per il suo quadrato e C per il suo cubo.
Un personaggio influente ma poco noto fu il francese Nicolas Chuquet, il cui libro Triparty en la science de nombres del 1484 discuteva tre argomenti matematici importanti: aritmetica, radici e incognite. La sua notazione per le radici era molto simile a quella di Cardano, ma egli cominciò a studiare in maniera sistematica il trattamento di potenze per l’incognita, usando gli apici per gli esponenti. Indicava le prime quattro potenze dell’incognita con premier, champs, cubiez e champs de champs. Per le nostre espressioni moderne 6x, 4x2 e 5x3 egli scriveva .6.1, .4.2, e .5.3. Usava la potenza zero e le potenze negative, scrivendo .2.0 e .3.1.m. dove noi scriveremmo 2 e 3x−1. In breve: usava la notazione esponenziale (apici) per le potenze dell’incognita, ma non aveva alcun simbolo esplicito per l’incognita in sé.
Quella mancanza fu colmata da Descartes: la sua notazione era molto simile alla nostra, con un’eccezione. Al posto della nostra formula
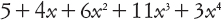
per esempio, Descartes scriveva
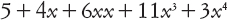
Questo significa che usava xx per il quadrato, anche se talvolta usava x2. Newton scriveva le potenze dell’incognita esattamente come facciamo noi adesso, compresi gli esponenti frazionari e negativi, come x3/2 per la radice quadrata di x3. Fu Gauss che infine abolì xx in favore di x2; e una volta che il Grande Maestro fece questo, tutti gli altri si adeguarono.
La logistica speciosa
L’algebra era nata come metodo per formulare in maniera sistematica i problemi aritmetici, ma al tempo di Viète aveva acquisito dignità di per sé. Prima di Viète, il simbolismo algebrico e la manipolazione erano visti come un modo per enunciare ed eseguire procedimenti algebrici, ma i numeri erano ancora il punto centrale. Viète fece una distinzione cruciale tra quella che chiamava la logistica speciosa e la logistica numerosa. Nella sua concezione, un’espressione algebrica rappresentava un’intera classe (specie) di espressioni aritmetiche. Era un concetto differente. Nella sua opera del 1591, In artem analyticam isagoge, Viète spiegava che l’algebra è un metodo per operare su forme generali, mentre l’aritmetica è un metodo per operare su numeri specifici.
Questo può sembrare un cavillo logico, ma la differenza concettuale era significativa. Per Viète, un calcolo algebrico come (nella nostra notazione)
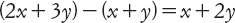
esprime un modo per manipolare espressioni simboliche. I singoli termini 2x + 3y e così via sono anch’essi oggetti matematici. Possono essere sommati, sottratti, moltiplicati e divisi senza mai essere considerati come rappresentazioni di numeri specifici. Per i predecessori di Viète, invece, quella stessa equazione era semplicemente una relazione numerica che era valida ogni volta che ai simboli x e y si sostituivano numeri particolari. L’algebra acquisì dunque una vita propria, come la matematica delle espressioni simboliche. Fu il primo passo verso la liberazione dell’algebra dalle catene dell’interpretazione matematica.
Quello che l’algebra fa per noi
I principali fruitori di algebra nel mondo moderno sono gli scienziati, che rappresentano le regolarità della natura con equazioni algebriche. Queste equazioni possono essere risolte per rappresentare quantità incognite in termini di quantità note. La tecnica è diventata così comune che nessuno si accorge di usare l’algebra.
L’algebra è stata persino applicata all’archeologia in un episodio di Time Team, quando l’intrepido archeologo televisivo vuole calcolare la profondità di un pozzo medievale. La prima idea è quella di buttare giù un oggetto, e calcolare il tempo impiegato a raggiungere il fondo: sei secondi. La formula algebrica in questo caso è

dove s è l’altezza, t il tempo impiegato per raggiungere il fondo, e g l’accelerazione dovuta alla gravità, circa 10 metri per secondo al quadrato. Considerando t = 6, la formula ci dice che il pozzo è profondo circa 180 metri.
Pensando di non ricordare bene la formula, che in realtà ricordano bene, i protagonisti di Time Team usano tre lunghi metri a nastro legati insieme.
La profondità misurata è in effetti molto vicina a 180 metri.
L’algebra entra in maniera più ovvia se conosciamo la profondità e vogliamo calcolare il tempo. Ora abbiamo da risolvere l’equazione per t in termini di s, per ottenere la soluzione
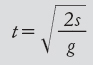
Sapendo che s = 180 metri per esempio, prevediamo che t sia la radice quadrata di 360/10, cioè la radice quadrata di 36, che è 6 secondi.