11.
Saldi fondamenti
Il calcolo infinitesimale ha senso
Nel 1800 i matematici e i fisici avevano trasformato il calcolo infinitesimale in uno strumento indispensabile per lo studio del mondo naturale, e i problemi che sorsero da questo collegamento condussero a una messe di nuovi concetti e metodi (per esempio, metodi di risoluzione di equazioni differenziali) che fecero del calcolo infinitesimale una delle più ricche e più attive aree di ricerca di tutta la matematica. La bellezza e la potenza del calcolo infinitesimale erano diventate innegabili. In ogni caso, le critiche del vescovo Berkeley in merito ai fondamenti logici rimasero senza risposta, e quando gli studiosi cominciarono ad affrontare argomenti più sofisticati, l’intero edificio cominciò a sembrare davvero traballante. Il primo brusco tentativo di usare le serie infinite, senza tener conto del loro significato, produsse sia risultati insensati sia indizi. I fondamenti dell’analisi di Fourier erano inesistenti, e diversi matematici annunciavano dimostrazioni di teoremi contraddittori. Termini come «infinitesimo» furono banditi senza essere definiti; i paradossi logici abbandonati; persino il significato della parola «funzione» fu messo in discussione. È chiaro che queste circostanze negative non potevano protrarsi all’infinito.
Per mettere ordine in tutto questo ci volle una mente chiara, e la buona volontà di sostituire l’intuizione con la precisione, anche se c’era da pagare un prezzo in termini di comprensibilità. I principali protagonisti furono Bernhard Bolzano, Augustin-Louis Cauchy, Niels Abel, Peter Dirichlet e, soprattutto, Karl Weierstrass. Grazie ai loro sforzi, nel 1900 anche le più complicate elaborazioni di serie, limiti, derivate e integrali potevano essere tranquillamente affrontate, in maniera accurata e senza paradossi. Fu fondata una nuova materia: l’analisi. Il calcolo infinitesimale divenne un aspetto fondamentale dell’analisi, ma concetti più sottili e più fondamentali, come quelli di continuità e di limite, guadagnarono la precedenza logica, ancorando le idee del calcolo infinitesimale. Gli infinitesimi furono banditi, completamente.
Fourier
Prima che Fourier comparisse sulla scena, i
matematici erano abbastanza contenti di sapere che cos’era una
funzione. Era un tipo di procedimento, f, che prendeva un
numero, x, e produceva un altro numero,
f(x). I numeri x che permettono di avere
una funzione sensata dipendono dalle caratteristiche di f.
Se f(x) = 1/x, per esempio, allora
x deve essere diverso da zero. Se 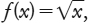 e lavoriamo con
i numeri reali, allora x deve essere positivo. Pressati
però a dare una definizione, i matematici tendevano a essere un po’
vaghi.
e lavoriamo con
i numeri reali, allora x deve essere positivo. Pressati
però a dare una definizione, i matematici tendevano a essere un po’
vaghi.
Le loro difficoltà, ora lo capiamo, derivavano dall’essere alle prese con molte caratteristiche diverse del concetto di funzione: non soltanto che cos’è una regola che associa un numero x a un altro numero f(x), ma quali proprietà quella regola possiede, come continuità, differenziabilità, capacità di essere rappresentata da un certo tipo di formula e così via.
In particolare, erano incerti sul come trattare le funzioni discontinue, come

Questa funzione salta all’improvviso da 0 a 1 quando x attraversa lo 0. C’era la diffusa convinzione che il salto derivasse in maniera ovvia dalla duplice definizione della formula: da f(x) = 0 a f(x) = 1. Allo stesso tempo si pensava che soltanto in questi casi si avesse un salto; che ogni formula definita in maniera unica evitasse tali salti, e che una piccola variazione in x determinasse sempre una piccola variazione in f (x).
Un’altra fonte di difficoltà veniva dalle funzioni complesse, per le quali, come abbiamo visto, funzioni naturali come la radice quadrata assumono due valori, e i logaritmi hanno un numero infinito di valori. Chiaramente il logaritmo deve essere una funzione, ma quando i valori sono in numero infinito, qual è la regola per ottenere f(z) da z? Sembrava esistesse un numero infinito di regole diverse, tutte ugualmente valide. Per risolvere queste difficoltà concettuali, i matematici dovevano osservarle bene da vicino per capire quanto la situazione reale fosse confusa. E fu Fourier che davvero li irritò, con la sua fantastica idea di scrivere ogni funzione come una serie infinita di seni e coseni, sviluppata in occasione delle sue ricerche sul flusso di calore.
L’intuizione fisica di Fourier gli suggerì che il suo metodo doveva essere davvero molto originale. In termini sperimentali, possiamo immaginare di mantenere una barra di metallo a 0 gradi per metà della sua lunghezza e a 10, 50 gradi o qualunque altro valore per l’altra metà. La fisica non sembra turbarsi per le funzioni discontinue, con formule che variano improvvisamente. La fisica, ad ogni modo, non lavora con le formule. Siamo noi che usiamo le formule per modellare la realtà fisica, ma si tratta soltanto di una tecnica, è il modo in cui ci piace pensare. Naturalmente la temperatura non sarà tanto precisa nel punto di incontro delle due regioni, ma i modelli matematici sono sempre approssimazioni della realtà fisica. Il metodo di Fourier delle serie trigonometriche, applicato a una funzione discontinua di questo tipo, sembra fornire risultati assolutamente sensati. Le barre di acciaio di fatto distribuivano la temperatura proprio come descriveva la loro equazione di calore, risolta usando serie trigonometriche. Nella sua Théorie analytique de la chaleur Fourier chiariva la sua posizione: «In generale, la funzione f(x) rappresenta una successione di valori o ordinate ognuna delle quali è arbitraria. Pensiamo che queste ordinate non siano soggette a una legge comune. Si succedono una dopo l’altra in una maniera qualsiasi».
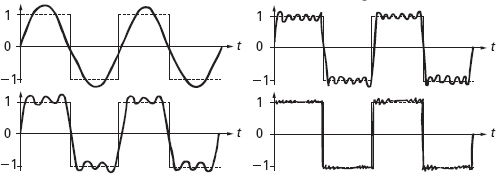
Figura 11.1
L’onda quadra e alcune delle approssimazioni di Fourier.
Parole sante; purtroppo la sua testimonianza in loro difesa non equivaleva a una dimostrazione matematica. Era, se possibile, ancora più sciatta del ragionamento usato da personaggi come Eulero e Bernoulli. Inoltre, se Fourier aveva ragione, allora la sua serie di fatto derivava una legge comune per le funzioni discontinue. La funzione precedente, con valori 0 e 1, ha una parente periodica, l’onda quadra. E l’onda quadra ha un’unica serie di Fourier, piuttosto bella, che funziona altrettanto bene nelle regioni in cui la funzione vale 0 e nelle regioni in cui la funzione vale 1. Di conseguenza, una funzione che sembra essere rappresentata da due leggi diverse può essere riscritta in termini di un’unica legge.
Gradualmente i matematici del XIX secolo cominciarono a separare le diverse questioni concettuali affrontate in questa complessa area. La prima era il significato del termine, un’altra riguardava i diversi modi di rappresentare una funzione: con una formula, una serie di potenze, una serie di Fourier o altro. Una terza questione riguardava le proprietà della funzione e una quarta questione stabiliva quali erano le rappresentazioni che garantivano determinate proprietà. Un unico polinomio, per esempio, definisce una funzione continua. Una singola serie di Fourier, come sembrava, poteva non definirla.
L’analisi di Fourier divenne presto il banco di prova per le idee sul concetto di funzione. Qui il problema assunse rilievi più netti e le distinzioni tecniche esoteriche si rivelarono importanti. E fu in un articolo sulle serie di Fourier, nel 1837, che Dirichlet introdusse la moderna definizione di funzione. Di fatto, egli concordava con Fourier: una variabile y è una funzione di un’altra variabile x se per ogni valore di x (in un intervallo determinato) è definito un unico valore di y. Dirichlet affermava in maniera esplicita che non era necessaria alcuna particolare legge o formula: è sufficiente che y sia specificata tramite una successione ben definita di operazioni matematiche, applicata a x. Quello che al tempo dovette sembrare un esempio estremo è un déjà vu, del 1829: una funzione f(x) che assume un valore quando x è razionale, e un valore diverso quando x è irrazionale. Questa funzione è discontinua in ogni punto. (Oggi funzioni di questo tipo sono considerate piuttosto tranquille: conosciamo comportamenti molto peggiori).
Per Dirichlet, la radice quadrata non era una funzione a due valori, ma due funzioni a un valore. Per x reale, è naturale, ma non fondamentale, prendere la radice quadrata positiva come uno dei due valori, e la radice quadrata negativa come l’altro. Per i numeri complessi, non esistono scelte naturali ovvie, anche se si può fare qualcosa per rendere la vita più semplice.
Funzioni continue
I matematici cominciavano ora a pensare che anche se spesso avevano enunciato definizioni del termine «funzione», erano soliti assumere proprietà aggiuntive che non seguivano dalla definizione. Per esempio, ipotizzavano che ogni formula sensata, come un polinomio, definisse automaticamente una funzione continua, ma non l’avevano mai dimostrato. Di fatto, non potevano dimostrarlo, perché non avevano definito il significato di «continuo». L’intera disciplina era costellata di vaghe intuizioni, la maggior parte delle quali erano sbagliate.
Il personaggio che per primo cercò di mettere ordine in tutto questo fu un prete boemo, filosofo e matematico. Il suo nome era Bernhard Bolzano. Questi attribuì un fondamento logico ragionevole alla maggior parte dei concetti basilari del calcolo infinitesimale: la principale eccezione derivò dal fatto che considerò scontata l’esistenza di numeri reali. Sostenne che numeri infinitesimi e infinitamente grandi non esistono, e dunque non possono essere usati, per quanto possano essere suggestivi. Fornì inoltre la prima definizione efficace di funzione continua: f è continua se la differenza f(x + a) − f(x) può essere resa piccola a piacere scegliendo a sufficientemente piccolo. Gli autori precedenti erano portati a sostenere affermazioni come «se a è infinitesimo allora f(x + a) − f(x) è infinitesimo». Per Bolzano invece, a era soltanto un numero, come tutti gli altri. Il punto centrale per lui era che ogni volta che specifichiamo quanto vogliamo piccola la differenza f(x + a) − f(x), dobbiamo allora specificare un valore opportuno per a. Non era necessario che lo stesso valore andasse bene in ogni caso.
Per esempio, quindi, f(x) = 2x è continua, perché 2(x + a) − 2x = 2a. Se vogliamo che 2a sia più piccolo di un certo numero determinato, per esempio 10−10, allora dobbiamo rendere a più piccolo di 10−10/2. Se tentiamo una funzione più complicata, come f(x) =x2, allora i particolari sono un po’ più complicati perché il giusto valore di a dipende da x e anche dal valore scelto, 10−10, ma qualunque matematico con un minimo di preparazione può calcolare il valore in pochi minuti. Usando questa definizione, Bolzano dimostrò – per la prima volta in assoluto – che una funzione polinomiale è continua. Per cinquant’anni però, nessuno ne se accorse. Bolzano aveva pubblicato il suo lavoro in una rivista che i matematici raramente leggevano, o consultavano. Oggi, al tempo di Internet, è difficile credere quanto fossero limitate le comunicazioni soltanto cinquant’anni fa, per non parlare di 180 anni fa.
Nel 1821 Cauchy disse più o meno la stessa cosa, ma usando una terminologia poco chiara. La sua definizione di continuità di una funzione f prevedeva che f(x) e f(x + a) differissero per una quantità infinitesima ogni volta che a era infinitesimo, e a prima vista assomigliava alla vecchia, mal definita impostazione. Per Cauchy però l’infinitesimo non era un unico numero che era in qualche modo infinitamente piccolo, ma una successione di numeri con andamento decrescente costante. Per esempio, la successione 0,1, 0,01, 0,001, 0,0001 e così via, è infinitesima nel senso di Cauchy, ma ogni singolo numero, come 0,0001, non è altro che un numero reale tradizionale, piccolo, magari, ma non infinitamente piccolo. Tenendo in considerazione questa terminologia, vediamo che il concetto di continuità di Cauchy equivale esattamente a quello di Bolzano.
Un altro che si oppose a un’analisi approssimativa dei processi infiniti fu Abel, il quale contestò che i matematici usassero le serie infinite senza verificare se le somme avessero un senso. Le sue obiezioni colpirono il segno, e gradualmente l’ordine emerse dal caos.
Limiti
Le idee di Bolzano diedero l’avvio a questi sviluppi. Egli rese possibile definire il limite di una successione infinita di numeri, e da quello la serie, che è la somma di una successione infinita. In particolare, il suo formalismo implicava che

prosegue per sempre, è una somma significativa, e il suo valore è esattamente 2. Non poco meno, non meno per un infinitesimo, esattamente 2.
Per vedere come funziona, supponiamo di avere una successione di numeri,
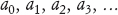
che continua all’infinito. Diciamo che an tende al limite a al tendere di n all’infinito se, per un numero qualsiasi ε > 0 esiste un numero N tale che la differenza tra an e a è minore di ε per ogni n > N. (Il simbolo ε, che è quello tradizionalmente usato, è la epsilon greca). Si noti che tutti i numeri in questa definizione sono finiti: non compaiono infinitesimi o infiniti.
Per sommare la serie infinita precedente, consideriamo le somme finite
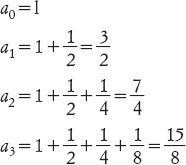
e così via. La differenza tra an e 2 è 1/2n. Per renderla minore di ε prendiamo n > N = log2(1/ε).
Una serie che ha un limite finito si dice convergente. Una somma finita è definita come il limite della successione di somme finite, ottenuta sommando un numero sempre maggiore di termini. Se tale limite esiste, la serie è convergente. Derivate e integrali sono semplicemente limiti di diverso tipo. Esistono – cioè hanno un senso matematico – a patto che quei limiti convergano. I limiti, proprio come sosteneva Newton, sono il valore cui si avvicinano certe grandezze quando un altro numero si avvicina all’infinito o a zero. Il numero non deve raggiungere l’infinito o zero.
Quello che l’analisi fece per loro
La fisica matematica del XIX secolo portò alla scoperta di molte importanti equazioni differenziali. In assenza di computer superveloci, capaci di trovare soluzioni numeriche, i matematici dell’epoca inventarono nuove funzioni speciali per risolvere queste equazioni. Queste funzioni sono usate ancora oggi. Un esempio è fornito dall’equazione di Bessel, definita per la prima volta da Daniel Bernoulli e in seguito generalizzata da Bessel. L’equazione ha la forma
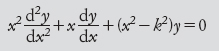
e le funzioni standard, come esponenziali, seni, coseni e logaritmi, non forniscono una soluzione.
In ogni caso, è possibile usare l’analisi per trovare soluzioni, sotto forma di serie di potenze. La serie di potenze determina nuove funzioni, le funzioni di Bessel. I tipi più semplici di funzioni di Bessel sono indicati come Jk(x), ma ne esistono molti altri. Le serie di potenze permettono il calcolo di Jk(x) con la precisione voluta.
Le funzioni di Bessel si presentano naturalmente in molti problemi relativi a cerchi e cilindri, come la vibrazione di una membrana circolare, la propagazione di onde elettromagnetiche in una guida d’onda cilindrica, la conduzione di calore in una barra metallica cilindrica, e la fisica dei laser.
Tutto il calcolo infinitesimale si fondava ora su basi solide. Il lato negativo era che ogni volta che si usava un procedimento di limite, bisognava essere sicuri che convergesse. Il modo migliore per farlo era dimostrare teoremi sempre più generali su quali tipi di funzioni sono continue, o differenziabili o integrabili, e quali successioni o serie convergono. Questo è quanto l’analista si apprestava a fare, ed è il motivo per cui noi non ci curiamo più delle difficoltà sottolineate dal vescovo Berkeley. È anche il motivo per cui non ragioniamo più sulle serie di Fourier: sappiamo bene quando convergono, quando non lo fanno e quindi in che senso convergono. Ci sono diverse variazioni sul tema fondamentale, e come serie di Fourier dobbiamo considerare quelle giuste.
Serie di potenze
Weierstrass comprese che le stesse idee erano
valide per i numeri complessi come per i numeri reali. Ogni numero
complesso z = x + iy ha un valore
assoluto 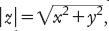 che per il teorema di
Pitagora è la distanza da 0 a z nel piano complesso. Se
misuriamo la dimensione di un’espressione complessa usando il suo
valore assoluto, allora i concetti nel mondo dei numeri reali di
limite, serie e così via, per come furono formulati da Bolzano,
possono subito essere trasferiti all’analisi complessa.
che per il teorema di
Pitagora è la distanza da 0 a z nel piano complesso. Se
misuriamo la dimensione di un’espressione complessa usando il suo
valore assoluto, allora i concetti nel mondo dei numeri reali di
limite, serie e così via, per come furono formulati da Bolzano,
possono subito essere trasferiti all’analisi complessa.
Weierstrass notò che un tipo particolare di serie infinita sembrava particolarmente utile. Si tratta della serie di potenze, e si presenta come un polinomio di grado infinito:
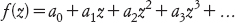
dove i coefficienti an sono numeri determinati. Weierstrass intraprese un vasto programma di ricerca, con l’obiettivo di fondare tutta l’analisi complessa sulle serie di potenze. Funzionò egregiamente.
Per esempio, possiamo definire la funzione esponenziale come
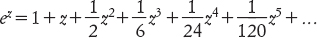
dove i numeri 2, 4, 6 e così via sono fattoriali: prodotti di interi consecutivi (per esempio 120 = 1 × 2 × 3 × 4 × 5). Eulero aveva già ottenuto questa formula in maniera euristica; ora Weierstrass poteva attribuirle un senso rigoroso. Di nuovo prendendo spunto dal libro di Eulero, Weierstrass fu allora in grado di mettere in relazione le funzioni trigonometriche con la funzione esponenziale, definendo
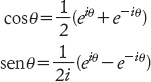
Tutte le consuete proprietà di queste funzioni seguivano dalla loro espressione in serie di potenze. Era anche possibile definire π, e dimostrare che eiπ= − 1, come Eulero aveva sostenuto. E questo allora significava che i logaritmi complessi facevano quello che Eulero aveva affermato. Tutto aveva un senso. L’analisi complessa non era soltanto un’estensione mistica dell’analisi reale: era un concetto ragionevole con una propria dignità. Di fatto, spesso era più semplice lavorare nel dominio complesso, e interpretare il risultato reale alla fine.
L’ipotesi di Riemann
Il più famoso problema irrisolto in tutta la matematica è l’ipotesi di Riemann, un problema dell’analisi complessa che nasce a proposito dei numeri primi ma ha ripercussioni in tutta la matematica.
Intorno al 1793 Gauss congetturò che il numero di primi minori di x fosse approssimativamente x/log x. Di fatto egli aveva suggerito un’approssimazione più accurata chiamata integrale logaritmico. Nel 1737 Eulero aveva notato un’interessante relazione tra la teoria dei numeri e l’analisi: la serie infinita
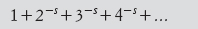
è uguale al prodotto, su tutti i primi p, della serie
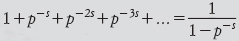
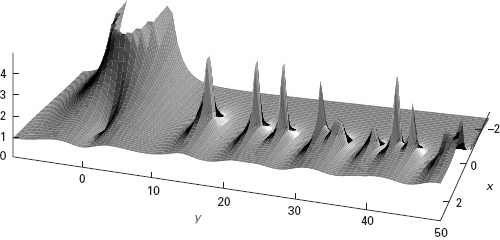
In questo caso dobbiamo considerare s > 1 perché la serie converga. Nel 1848 Pafnuty Chebyshev si avvicinò in qualche modo a una dimostrazione della congettura di Gauss, usando una funzione complessa collegata alla serie di Eulero, in seguito chiamata funzione zeta ζ(z). Il ruolo di questa funzione fu chiarito da Riemann nel suo articolo del 1859 Über die Anzahl der Primzahlen unter einer gegebenen Grösse. Riemann mostrò che le proprietà statistiche dei primi sono strettamente collegate con gli zeri della funzione zeta, cioè le soluzioni, z, dell’equazione ζ(z) = 0.
Nel 1869 Jacques Hadamard e Charles de la Vallée Poussin usarono la funzione zeta per dimostrare il teorema dei numeri primi. Il passo principale consiste nel mostrare che ζ(z) è diversa da zero per tutti gli z della forma 1 + it. Maggiore è il controllo che possiamo avere sulla posizione degli zeri della funzione zeta, più sappiamo dei primi. Riemann ipotizzò che tutti gli zeri, diversi da quelli banali per interi pari negativi, giacciono sulla retta critica z = 1/2 ± it.
Nel 1914 Hardy dimostrò che su questa retta giace un numero infinito di zeri. Estese dimostrazioni al computer supportano altresì la congettura. Tra il 2001 e il 2005 il programma ZetaGrid di Sebastian Wedeniwski ha verificato che i primi 100 miliardi di zeri si trovano sulla retta critica.
L’ipotesi di Riemann era parte del Problema 8 nel famoso elenco compilato da Hilbert sui 23 grandi problemi matematici irrisolti, e figura tra i Millenium Prize Problems del Clay Mathematics Institute.
Per Weierstrass, tutto questo era soltanto l’inizio: la prima fase di un ampio programma. Quello che però importava era porre correttamente le fondamenta. Una volta fatto questo, gli argomenti più sofisticati sarebbero facilmente seguiti.
Weierstrass aveva le idee particolarmente chiare, e poteva vedere come proseguire senza confondersi attraverso complicate combinazioni di limiti e derivate e integrali. Riusciva anche a individuare le potenziali difficoltà. Uno dei suoi più stupefacenti teoremi dimostra che esiste una funzione f(x) di una variabile reale x, che è continua in ogni punto, ma non è differenziabile in alcun punto. Il grafico di f è un’unica curva ininterrotta, ma una curva così sinuosa da non avere una tangente ben definita in alcun punto. I suoi predecessori non ci avrebbero creduto: i suoi contemporanei si chiesero a che cosa servisse. I suoi successori svilupparono questo concetto in una delle più eccitanti nuove teorie del XX secolo, i frattali.
Ma tratteremo questa storia più dettagliatamente in seguito.
Una solida base
I primi inventori del calcolo infinitesimale si avvicinarono piuttosto bruscamente alle operazioni infinite. Eulero aveva assunto che le serie di potenze fossero come i polinomi, e aveva applicato questa ipotesi con effetti devastanti. Nelle mani dei comuni mortali però, questo tipo di ipotesi può facilmente condurre a risultati insensati. Anche Eulero aveva fatto alcune affermazioni assolutamente sciocche. Per esempio, era partito dalla serie di potenze
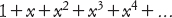
che dà come somma 1/(1 − x), posto x = − 1, per dedurre che
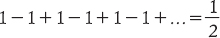
che non ha senso. La serie di potenze non converge a meno che x non sia strettamente compreso tra − 1 e 1, come spiega bene la teoria di Weierstrass.
Quello che l’analisi fa per noi
L’analisi è usata in biologia per studiare la crescita delle popolazioni di organismi. Un semplice esempio è fornito dal modello logistico o di Verhulst-Pearl. In questo caso la variazione nella popolazione, x, in funzione del tempo t è modellata da un’equazione differenziale
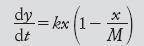
dove la costante M è la capacità massima, cioè la popolazione massima sostenibile dall’ambiente.
Metodi analitici tradizionali producono la soluzione esplicita
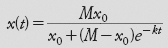
che è chiamata curva logistica. Il corrispondente modello di crescita inizia con un aumento rapido (esponenziale), ma quando la popolazione raggiunge metà della capacità massima comincia a stabilizzarsi, e alla fine si attesta sulla capacità massima.
Questa curva non è del tutto realistica, anche se si adatta molto bene a diverse popolazioni reali. Modelli più complicati dello stesso tipo forniscono un migliore adattamento con i dati reali. Anche il consumo da parte degli uomini delle risorse umane può seguire un modello simile alla curva logistica, rendendo possibile stimare la domanda futura, e il tempo di durata delle risorse.
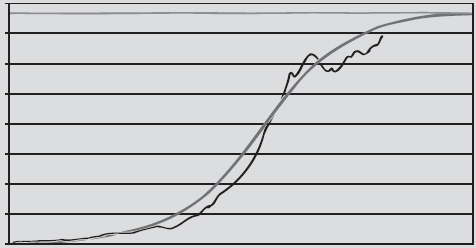
Consumo mondiale di greggio, 1900-2000: curva regolare, equazione logistica; curva frastagliata, dati reali.
Figura 11.2
Valore assoluto della funzione zeta di Riemann.
L’attenta valutazione di obiezioni come quelle sollevate dal vescovo Berkeley permise alla lunga di arricchire la matematica e di porla su un saldo fondamento. Più complicate si facevano le teorie, più importante era avere la sicurezza di poggiare su basi solide.
Oggi, la maggior parte dei fruitori di matematica ancora una volta ignora questi dettagli, ma sa che sono stati ponderati e che tutto quel che sembra ragionevole ha probabilmente una giustificazione rigorosa. Devono ringraziare Bolzano, Cauchy e Weierstrass per questa sicurezza. Nel frattempo, i matematici di professione continuano a sviluppare concetti rigorosi sui processi infiniti. Esiste anche un movimento, noto con il nome di analisi non standard, propenso a far rivivere il concetto di infinitesimo, ed è del tutto rigoroso e utile dal punto di vista tecnico per alcuni problemi altrimenti intrattabili. Evita contraddizioni logiche considerando gli infinitesimi come un nuovo tipo di numero, non un numero reale convenzionale. Nello spirito, è vicino al modo di pensare di Cauchy. Rimane una specializzazione di minoranza, ma tenetela d’occhio.