18.

Quanto è probabile?

L’approccio razionale al caso

Nel XX secolo e nei primi anni del XXI la matematica ha avuto uno sviluppo esplosivo. Abbiamo avuto più scoperte matematiche negli ultimi cento anni che in tutta la storia precedente dell’umanità. Anche per presentarle soltanto a grandi linee servirebbero migliaia di pagine, e siamo così costretti a proporre pochi assaggi dell’enorme quantità di materiale disponibile.

Una branca della matematica particolarmente nuova è la teoria della probabilità, che studia le possibilità associate con eventi casuali. È la matematica dell’indeterminazione. Le età precedenti avevano scalfito la superficie, con i calcoli combinatori delle probabilità nei giochi d’azzardo e alcuni metodi per migliorare l’accuratezza delle osservazioni astronomiche a dispetto degli errori di misurazione, ma soltanto all’inizio del XX secolo la teoria della probabilità si impose come una disciplina a sé.

Probabilità e statistica

Oggi, la teoria della probabilità è un’area importante della matematica, e il suo ramo applicato, la statistica, ha un importante influsso sulla nostra vita quotidiana, forse anche più importante rispetto ad altre branche importanti della matematica. La statistica è una delle principali tecniche di analisi in campo medico. Nessun farmaco è immesso sul mercato, e nessuna terapia è introdotta in un ospedale, prima che i trial clinici non ne abbiano garantito la sicurezza e l’efficacia. La sicurezza in questo caso è un concetto relativo: le terapie possono essere praticate su pazienti affetti da malattie altrimenti letali, qualora le possibilità di successo siano troppo basse in casi meno seri.

La teoria della probabilità può rivelarsi anche l’area della matematica più ampiamente fraintesa, e abusata. Se usata in maniera appropriata e intelligente offre però un importante contributo al benessere dell’umanità.

Giochi di probabilità

Alcune questioni probabilistiche risalgono all’antichità. Nel Medioevo, venne analizzata la probabilità di ottenere i diversi numeri in seguito al lancio di due dadi. Per capire come funziona, iniziamo con un dado. Ipotizzando che il dado non sia truccato – un concetto che è difficile da capire – ognuno dei sei numeri 1, 2, 3, 4, 5 e 6 dovrebbe presentarsi un numero uguale di volte, alla lunga. Sul breve termine, l’eguaglianza è impossibile: il primo lancio darà come risultato uno di quei numeri, per esempio. Di fatto, dopo sei lanci è in realtà piuttosto improbabile che sia uscito ogni numero esattamente una volta. In una lunga serie di lanci però, o prove, ci aspettiamo che ogni numero si sia presentato esattamente una volta su sei, vale a dire con probabilità 1/6. Se questo non è accaduto, molto facilmente il dado era truccato.

Un evento con probabilità 1 è certo, e uno con probabilità 0 è impossibile. Le probabilità hanno tutte un valore compreso tra 0 e 1, e la probabilità di un evento rappresenta la frazione di prove in cui l’evento in esame si è presentato.

Torniamo ora al problema medievale. Supponiamo di lanciare simultaneamente due dadi (come in molti giochi da craps a Monopoli™). Qual è la probabilità che la loro somma sia 5? Il risultato di diverse argomentazioni, e di alcuni esperimenti, è che la risposta è 1/9. Perché? Supponiamo di distinguere i due dadi, colorandone uno di blu e l’altro di rosso. Ogni dado può presentare indipendentemente sei numeri diversi, per un totale di 36 possibili coppie di numeri, tutte equamente probabili. Le combinazioni (blu + rosso) che danno come risultato 5 sono 1 + 4, 2 + 3, 3 + 2, 4 + 1. questi sono casi distinti perché il dado blu produce risultati distinti in ogni caso, e lo stesso vale per il dado rosso. Sul lungo termine ci aspettiamo allora di trovare una somma di 5 in quattro casi su 36, con una probabilità di 4/36 = 1/9.

Un altro antico problema, con un’evidente applicazione pratica, riguarda il modo di dividere la posta in un gioco di probabilità se la partita è interrotta per qualche ragione. Gli algebristi rinascimentali Pacioli, Cardano e Tartaglia scrissero tutti sull’argomento. In seguito il cavalier de Meré pose a Pascal lo stesso interrogativo, e Pascal e Fermat si scambiarono diverse lettere sull’argomento.

Da questo primo lavoro si comprese in maniera implicita che cosa sono le probabilità e come calcolarle. Tutta la questione era però mal posta e confusa.

Combinazioni

Una definizione operativa della probabilità di un certo evento è data dalla frazione di casi in cui questo si presenta. Se gettiamo un dado, e le sei facce sono equiprobabili, allora la probabilità di ottenere una particolare faccia è 1/6. Molti dei primi lavori sulla probabilità poggiavano sul calcolo del numero di modi in cui un evento si poteva presentare, per poi dividere il valore per il numero totale di possibilità.

Un problema fondamentale a questo punto è quello delle combinazioni. Dato, per esempio, un mazzetto di sei carte, quanti sottoinsiemi diversi di quattro carte possiamo formare? Uno dei metodi prevede di elencare questi sottoinsiemi: se le carte sono 1-6, allora abbiamo

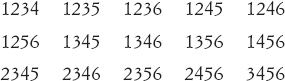
per un numero di 15 combinazioni. Questo metodo però è troppo laborioso se abbiamo un grande numero di carte, ed è meglio trovare un procedimento più sistematico.

Immaginiamo di scegliere i quattro membri del sottoinsieme, uno alla volta. Possiamo scegliere il primo in sei modi, il secondo soltanto in cinque (poiché una carta è stata eliminata), il terzo in quattro modi, il quarto in tre modi. Il numero totale di scelte, in questo ordine, è 6 × 5 × 4 × 3 = 360. Ogni sottoinsieme è contato comunque 24 volte: infatti come 1234 troviamo 1243, 2134, e così via, e ci sono 24 (4 × 3 × 2) modi di disporre quattro oggetti. La risposta corretta è dunque 360/24, che è uguale a 15. Questo ragionamento mostra che il numero di modi di scegliere m oggetti da un totale di n oggetti è

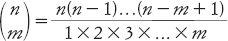
Le espressioni di questo tipo sono chiamate coefficienti binomiali, perché si presentano anche in algebra. Se li disponiamo in una tabella, in modo che la riga n-esima contenga i coefficienti binomiali

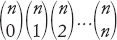
allora il risultato ha la forma mostrata nella figura 18.1.

Nella settima riga leggiamo i numeri 1, 6, 15, 20, 15, 6, 1.

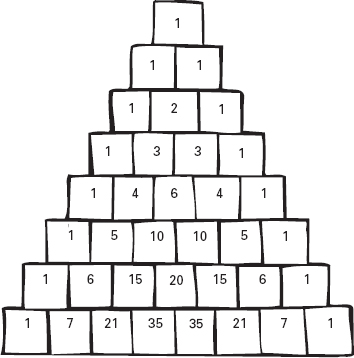
Figura 18.1

Il triangolo di Pascal.

Facciamo il confronto con la formula

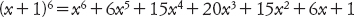
e vediamo che gli stessi numeri compaiono come coefficienti. Questa non è una coincidenza.

Il triangolo di numeri è detto triangolo di Pascal perché fu studiato da Pascal nel 1655. Era comunque già noto molto tempo prima: si ritrova nel 950 circa in un commentario su un antico testo indiano chiamato Chandas Shastra. Era anche noto ai matematici persiani Al-Karaji e Omar Khayyām, e nell’Iran moderno è chiamato triangolo di Khayyām.

Teoria della probabilità

I coefficienti binomiali furono usati con ottimi risultati nel primo libro di probabilità: l’Ars Conjectanti di Jacob Bernoulli (1713, postuma). Il curioso titolo è spiegato nel testo:

Noi definiamo l’arte di congetturare, o stocastica, come quella di valutare il più esattamente possibile le probabilità delle cose, affinché sia sempre possibile, nei nostri giudizi e nelle nostre azioni, orientarci su quella che risulta la scelta migliore, più appropriata, più sicura, più prudente; il che costituisce il solo oggetto della saggezza del filosofo e della prudenza del politico.

Una traduzione forse più appropriata del titolo sarebbe l’arte dell’azzeccarci.

Bernoulli dava per scontato che un numero sempre maggiore di tentativi portasse a una stima sempre migliore della probabilità:

Supponiamo che in un’urna, senza che tu lo sappia, ci siano 3000 sassolini bianchi e 2000 neri. Procedendo per tentativi tu vuoi determinare il loro rapporto, estraendo un sassolino dopo l’altro (e rimettendolo nell’urna dopo averlo estratto) e osservando quante volte esce un sassolino bianco e quante uno nero. Ci si chiede se tu puoi ripetere l’operazione tanto spesso, da far sì che diventi dieci, cento, mille volte più probabile […] che il numero delle volte in cui estrai un sassolino bianco rispetto al numero delle volte in cui estrai un sassolino nero assuma lo stesso rapporto di 3:2 che hanno tra loro i sassolini nell’urna, o questi numeri non formino un tutt’altro rapporto diverso da quello.

Qui Bernoulli poneva una domanda fondamentale, e inventava anche un esempio illustrativo classico, quello delle palline in un’urna. Egli chiaramente credeva che un rapporto di 3:2 fosse il risultato ragionevole, ma riconosceva anche che gli esperimenti reali si sarebbero soltanto avvicinati a questo rapporto. Era però convinto che con un numero sufficiente di tentativi, questa approssimazione avrebbe dovuto migliorare sempre più.

Sorge una difficoltà a questo punto, che ostacolò tutta la ricerca per lungo tempo. In un esperimento del genere, è certamente possibile che per puro caso ogni sassolino estratto sia bianco. Non abbiamo quindi una garanzia veloce e sicura che il rapporto debba sempre tendere a 3:2. Al massimo possiamo dire che con probabilità molto alta, i numeri dovrebbero avvicinarsi a quel rapporto. Ora però si pone un pericolo di logica circolare: usiamo i rapporti osservati nei tentativi per dedurre le probabilità, ma possiamo anche usare le probabilità per arrivare a quella deduzione. Come possiamo osservare che la probabilità che tutti i sassolini siano bianchi è molto piccola? Se decidiamo per un grande numero di tentativi, siamo di fronte alla possibilità di un risultato fuorviante, per la stessa ragione; e l’unica via di uscita sembra quella di effettuare un numero maggiore di tentativi per mostrare che questo evento è di per sé altamente improbabile. Siamo caduti in quella che assomiglia terribilmente a una regressione infinita.

Per fortuna, i primi studiosi di teoria della probabilità non permisero che questa difficoltà logica li fermasse. Come nel caso del calcolo infinitesimale, sapevano che cosa volevano fare, e come farlo. Una giustificazione filosofica era meno interessante rispetto alla scoperta delle risposte.

Il libro di Bernoulli conteneva una messe di importanti idee e risultati. Uno di questi, la legge dei grandi numeri, definisce esattamente in che senso i rapporti delle osservazioni a lungo termine corrispondono alle probabilità. Sostanzialmente, Bernoulli dimostra che la probabilità che il rapporto non diventi molto vicino alla probabilità corretta tende a zero quando il numero di tentativi cresce senza limite.

Un altro teorema fondamentale può essere visto in termini del lancio ripetuto di una moneta truccata, con una probabilità p di ottenere testa, e q = 1 − p di ottenere croce. Se la moneta è lanciata due volte, qual è la probabilità di ottenere esattamente 2, 1 o 0 teste? La risposta di Bernoulli fu p², 2pq e q². Questi sono i termini che si ottengono dall’espansione del binomio (p + q)² come p² + 2pq + q². In maniera analoga, se la moneta è lanciata tre volte, le probabilità di avere 3, 2, 1 oppure 0 teste sono i termini successivi in (p + q)³ = p³ + 3p²q + 3pq² + q³.

In termini più generali, se la moneta è lanciata n volte, la probabilità di avere esattamente m teste è uguale a

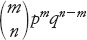
cioè il termine corrispondente nell’espansione di (p + q)ⁿ.

Tra il 1730 e il 1738 Abraham De Moivre estese il lavoro di Bernoulli alle monete truccate. Quando m e n sono grandi, è difficile calcolare esattamente il coefficiente binomiale, e De Moivre derivò una formula approssimata, che mette in relazione la distribuzione binomiale di Bernoulli con quella che ora chiamiamo funzione errore o distribuzione normale

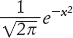
De Moivre fu di fatto il primo a esplicitare questa relazione, che si rivelò fondamentale per lo sviluppo tanto della teoria della probabilità quanto della statistica.

La definizione di probabilità

Un importante problema concettuale nella teoria della probabilità fu la definizione della probabilità. Anche esempi semplici – casi di cui tutti conoscevano la risposta – presentavano difficoltà logiche. Se lanciamo una moneta allora, nel lungo termine, ci aspettiamo un numero uguale di teste e di croci, per cui la probabilità di ognuno dei due casi è 1/2. Per essere più precisi, questa è la probabilità nell’ipotesi che la moneta sia buona. Una moneta truccata potrebbe presentare sempre testa. Che cosa significa però «buona»? Presumibilmente, che testa e croce siano egualmente probabili. L’espressione «egualmente probabili» fa però riferimento alle probabilità. La logica sembra circolare. Per poter definire la probabilità, dobbiamo sapere che cos’è la probabilità.

La via di uscita a questo impasse risale a Euclide, e fu perfezionata dagli algebristi della fine del XIX secolo e dell’inizio del XX. Definiamo un sistema di assiomi. Smettiamola di chiederci cosa siano le probabilità. Stiliamo un elenco delle proprietà che riteniamo le probabilità debbano avere, e consideriamo che siano assiomi. Deduciamo tutto il resto da questi.

La questione era: quali sono gli assiomi giusti? Se le probabilità si riferiscono a insiemi finiti di eventi, questa domanda ha una risposta abbastanza semplice. Le applicazioni della teoria della probabilità implicano però spesso la scelta da un insieme potenzialmente infinito di possibilità. Se misuriamo l’angolo tra due stelle, per esempio, allora in linea di principio questo può avere un valore reale qualunque compreso tra 0° e 180°. I numeri reali sono infiniti. Se lanciamo una freccetta su un bersaglio, in modo che alla lunga questa abbia la stessa probabilità di colpire qualsiasi punto su di esso, allora la probabilità di colpire una data regione dovrebbe essere data dall’area di quella regione divisa per l’area totale del bersaglio. Il bersaglio contiene però un numero infinito di punti, e anche un numero infinito di regioni.

Queste difficoltà causavano problemi di ogni tipo, e paradossi di ogni tipo. Alla fine furono risolte con una nuova idea mutuata dall’analisi, il concetto di misura.

Gli analisti che studiavano la teoria dell’integrazione reputarono necessario andare oltre Newton, e definire concetti via via più sofisticati del significato di funzione integrabile, e di integrale. Dopo una serie di tentativi da parte di diversi matematici, Henri Lebesgue riuscì a definire un tipo molto generale di integrale, ora chiamato integrale di Lebesgue, con diverse proprietà simpatiche e utili in termini analitici.

Il punto centrale nella sua definizione era la misura di Lebesgue, che è un modo per assegnare un concetto di lunghezza a sottoinsiemi della retta reale molto complicati. Supponiamo che l’insieme sia costituito da intervalli che non si sovrappongono di lunghezze 1, 1/2, 1/4, 1/8 e così via. Questi numeri formano una serie convergente, con somma 2. Lebesgue sosteneva di conseguenza che questo insieme avesse misura 2. Il concetto di Lebesgue ha una nuova caratteristica: è numerabilmente additivo. Se mettiamo insieme una collezione infinita di insiemi che non si sovrappongono, e se questa collezione è numerabile nel senso di Cantor, con cardinalità ℵ₀, allora la misura dell’insieme completo è la somma della serie infinita formata dalle misure dei singoli insiemi.

Per molti versi l’idea di una misura era più importante rispetto all’integrale al quale essa conduceva. In particolare, la probabilità è una misura. Questa proprietà era stata resa esplicita negli anni trenta del Novecento da Andrej Kolmogorov, il quale aveva enunciato alcuni assiomi per le probabilità. Più precisamente, egli aveva definito uno spazio di probabilità. Questo comprende un insieme X, una collezione B di sottoinsiemi di X chiamati eventi, e una misura m su B. Gli assiomi dicono che m è una misura, e che m(X) = 1 (cioè che la probabilità che qualcosa accada è sempre 1). La collezione B deve anche soddisfare alcune proprietà della teoria degli insiemi che consentono di supportare una misura.

Per un dado, l’insieme X è formato dai numeri 1-6, e l’insieme B contiene ogni sottoinsieme di X. La misura di un insieme qualunque Y in B è il numero di membri di Y, diviso per 6. Questa misura è coerente con l’idea intuitiva che ogni faccia del dado si presenti con probabilità 1/6. L’uso di una misura implica però che consideriamo non soltanto facce, ma insiemi di facce. La probabilità associata con un insieme del genere Y è la probabilità che si presenti una certa faccia in Y. Intuitivamente, questa è la dimensione di Y divisa per 6.

Con questa semplice idea, Kolmogorov mise la parola fine a una controversia spesso accesa durata centinaia di anni, e diede vita a una teoria rigorosa della probabilità.

Dati statistici

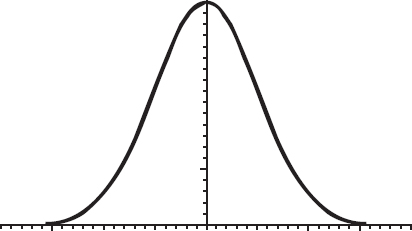
Il braccio applicato della teoria della probabilità è la statistica, che usa le probabilità per analizzare i dati del mondo reale. Si sviluppò a partire dall’astronomia del XVIII secolo, quando fu necessario stimare gli errori di osservazione. Dal punto di vista empirico e teorico, tali errori sono distribuiti secondo la funzione errore o distribuzione normale, spesso chiamata curva a campana per la sua forma. In questo caso l’errore è misurato in orizzontale, con il valore zero al centro, mentre l’altezza della curva rappresenta la probabilità di un errore di entità data. Piccoli errori sono abbastanza probabili, mentre quelli grandi sono molto improbabili.

Nel 1835 Adolphe Quetelet usò la curva a campana per modellare alcuni dati sociali: nascite, decessi, divorzi, crimini e suicidi. Scoprì che, anche se imprevedibili per i singoli, quando sono osservati per un’intera popolazione gli eventi di questo tipo seguono un modello statistico. Diede corpo a questa idea in termini dell’«uomo medio», un individuo di fantasia che era medio sotto ogni aspetto. Per Quetelet, l’uomo medio non era soltanto un concetto matematico: era l’obiettivo di una giustizia sociale.

A partire dal 1880 circa le scienze sociali cominciarono a sfruttare ampiamente i concetti statistici, in particolare la curva a campana, in sostituzione degli esperimenti. Nel 1865 Francis Galton studiò l’ereditarietà umana. Che relazione ha l’altezza di un figlio rispetto a quella dei genitori? Che dire del peso, o delle capacità intellettuali? Adottò la curva a campana di Quetelet, ma la vide come un metodo per separare popolazioni distinte, non come un imperativo morale. Se certi dati mostravano due picchi, invece che l’unico picco della curva a campana, allora quella popolazione doveva essere composta da due sottopopolazioni distinte, ognuna con la propria curva a campana. Nel 1877 le ricerche di Galton lo condussero a inventare l’analisi di regressione, una tecnica usata per confrontare un insieme di dati con un altro per trovare la relazione più probabile.

Figura 18.2

La curva a campana.

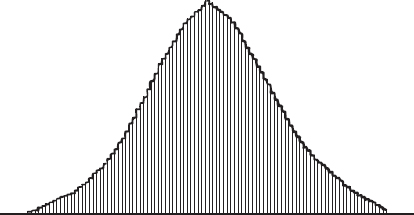
Figura 18.3

Il grafico di Quetelet relativo al numero di persone che hanno una data altezza: l’altezza è indicata in orizzontale, il numero di persone in verticale.

Un’altra figura di spicco fu Francis Ysidro Edgeworth. Questi non aveva la percezione di Galton, ma era un tecnico molto più abile, e fondò le idee di Galton su una solida base matematica. Un terzo personaggio fu Karl Pearson, che sviluppò notevolmente la matematica. Pearson ebbe però soprattutto un ruolo commerciale: convinse il mondo esterno dell’utilità della statistica.

Newton e i suoi successori avevano dimostrato che la matematica può essere una maniera molto efficace per comprendere le regolarità della natura. L’invenzione della teoria della probabilità, e del suo braccio applicato, la statistica, facevano lo stesso con le irregolarità della natura. È degno di nota che gli eventi casuali rivelino modelli numerici. Questi modelli si mostrano però soltanto in quantità statistiche, come tendenze e medie a lungo termine. Fanno previsioni, ma queste riguardano la probabilità che qualche evento accada oppure no. Non sono in grado di prevedere se accadrà. Nonostante questo, la probabilità è ora una delle tecniche matematiche più ampiamente usate, adottata dalla scienza e dalla medicina per garantire che ogni deduzione derivata dalle osservazioni sia significativa, piuttosto che un modello fittizio risultante da associazioni casuali.