12.
Triangoli impossibili
La geometria di Euclide è l’unica possibile?
Il calcolo infinitesimale fu basato su principi geometrici, ma la geometria fu ridotta a calcoli simbolici, che furono allora formalizzati come analisi. Ad ogni modo, in matematica si stava anche sviluppando il ruolo della visualizzazione, in una direzione nuova e all’inizio piuttosto sbalorditiva. Per più di 2000 anni il nome di Euclide è stato sinonimo di geometria. I successori ne svilupparono le idee, soprattutto quelle contenute nella sua opera sulle sezioni coniche, ma non operarono un cambio radicale al concetto stesso di geometria. Di fatto, l’ipotesi era che potesse esistere soltanto una geometria, quella di Euclide, e che questa fosse una descrizione matematica esatta della vera geometria dello spazio fisico. I matematici trovavano difficile persino concepire un’alternativa.
Non poteva durare.
Geometria sferica e proiettiva
Il primo significativo allontanamento dalla geometria euclidea ebbe spunto da una questione molto pratica di navigazione. Sulle distanze brevi, la Terra è quasi piatta, e le sue caratteristiche fisiche sono rappresentabili su un piano. Quando però le navi effettuano viaggi più lunghi, occorre tener conto della forma reale del pianeta. Molte civiltà antiche sapevano che la Terra è rotonda: gli indizi sono molti, dal modo in cui le navi sembrano scomparire all’orizzonte, all’ombra del pianeta sulla Luna durante le eclissi lunari. In genere si assumeva che la Terra fosse una sfera perfetta.
In realtà, la sfera è leggermente appiattita: il diametro all’equatore è 12 756 km, mentre ai poli è 12 714 km. La differenza è relativamente piccola, una parte su 300. Al tempo in cui i naviganti erano soliti commettere errori di diverse centinaia di chilometri, una Terra sferica forniva un modello matematico assolutamente accettabile. A quel tempo, comunque, l’enfasi era sulla trigonometria piuttosto che sulla geometria sferica: i dettagli essenziali dei calcoli di navigazione, non l’analisi logica della sfera come tipo di spazio. Poiché la sfera si colloca naturalmente in uno spazio euclideo tridimensionale, nessuno pensava che la geometria sferica fosse diversa da quella euclidea. Qualunque differenza era il risultato della curvatura della Terra. La geometria dello spazio in sé rimaneva euclidea.
Un allontanamento più significativo da Euclide venne con l’introduzione, a partire dai primi anni del XVII secolo, della geometria proiettiva. La questione non nasceva dalla scienza ma dall’arte: gli studi teorici e applicativi sulla prospettiva condotti dagli artisti del Rinascimento italiano. Lo scopo era quello di far sì che i dipinti apparissero più realistici: il risultato fu un nuovo modo di pensare la geometria. Di nuovo però questo sviluppo poteva essere visto come un’innovazione all’interno del contesto classico euclideo. Riguardava il nostro modo di vedere lo spazio, non lo spazio.
La scoperta che Euclide non era da solo, che potevano esistere tipi diversi di geometria consistenti dal punto di vista logico, in cui molti dei teoremi di Euclide smettevano di essere validi, emerse da un rinnovato interesse nei fondamenti logici della geometria, discussi e sviluppati a partire dalla metà del XVIII fino alla metà del XIX secolo. La questione principale era il quinto postulato di Euclide, che, in maniera maldestra, affermava l’esistenza di rette parallele. I diversi tentativi di dedurre il quinto postulato dagli altri assiomi di Euclide condussero alla fine alla conclusione che non fosse possibile alcuna deduzione del genere. Esistono geometrie consistenti diverse da quella euclidea. Oggi, queste geometrie non euclidee sono strumenti indispensabili nella matematica pura e nella fisica matematica.
Geometria e arte
In Europa, tra il 300 e il 1600 la geometria visse un momento difficile. La ripresa della geometria come argomento di studio fu stimolata dal problema della prospettiva in campo artistico: come riprodurre un mondo tridimensionale su una tela bidimensionale in maniera realistica.
Gli artisti del Rinascimento non creavano soltanto dipinti. Molti si dedicavano alla realizzazione di opere di ingegneria, per scopi pacifici o di guerra. La loro arte aveva un lato pratico, e la geometria della prospettiva era una ricerca pratica, applicabile all’architettura come alle arti visive. C’era anche un crescente interesse per l’ottica, la matematica della luce, che si ampliò una volta che furono inventati il cannocchiale e il microscopio. Il primo artista di rilievo a pensare alla matematica della prospettiva fu Filippo Brunelleschi. Di fatto, la sua arte fu perlopiù un tramite per la sua matematica. Un libro seminale è il Della pittura di Leon Battista Alberti, scritto nel 1435 e pubblicato nel 1511. Alberti cominciava facendo alcune importanti, e relativamente innocue, semplificazioni: l’atteggiamento tipico di un vero matematico. La visione umana è un argomento complesso. Per esempio, noi usiamo due occhi separati di poco per generare immagini stereoscopiche, che forniscono la sensazione di profondità. Alberti semplificò la realtà ipotizzando un unico occhio con una pupilla a punta di spillo, che funzionava come il foro dell’obiettivo di una macchina fotografica. Immaginò un artista che dipinge una scena, sistemando il suo cavalletto e tentando di far sì che l’immagine sulla tela corrisponda a quella percepita dal suo (unico) occhio. La tela e la realtà proiettano le loro immagini sulla retina, dietro l’occhio. Il modo più semplice (concettuale) di garantire una perfetta corrispondenza è rendere la tela trasparente, guardare attraverso di essa da una posizione fissa e disegnare sulla tela esattamente quello che vede l’occhio. Allora la scena tridimensionale è proiettata sulla tela. Si unisca ogni particolare della scena con l’occhio per mezzo di una linea diritta, e si noti dove questa linea incontra il piano della tela: quello è il punto in cui disegnare quel particolare.
Questa idea non è del tutto praticabile se presa alla lettera, anche se alcuni artisti fecero proprio così, usando un materiale traslucido, o vetro, al posto della tela. Spesso iniziarono il lavoro in questo modo, trasferendo poi il contorno ottenuto sulla tela per completare il dipinto vero e proprio. Un approccio più pratico consiste nell’usare questa formulazione concettuale per mettere in relazione la geometria della scena tridimensionale con quella dell’immagine bidimensionale. La geometria euclidea ordinaria studia caratteristiche che rimangono invariate per traslazioni rigide, come lunghezze e angoli. Euclide non la formulò in quel modo, ma il suo uso dei triangoli congruenti come strumento fondamentale ha lo stesso effetto. (Questi sono triangoli di uguale dimensione e forma, ma in posizioni diverse). Analogamente, la geometria della prospettiva si riduce a caratteristiche che rimangono invariate per proiezione. È facile vedere che le lunghezze e gli angoli non si comportano in questo modo. Possiamo coprire la Luna con un dito, e dunque le lunghezze possono cambiare. Gli angoli non se la passano meglio: quando osserviamo l’angolo di un edificio, un angolo retto, questo appare come un angolo retto soltanto se lo osserviamo di fronte.
Quali proprietà delle figure geometriche, allora, sono preservate per proiezione? Quelle più importanti sono così semplici che è facile perderne di vista il significato. I punti rimangono punti. Le linee diritte rimangono diritte. L’immagine di un punto su una linea diritta rimane sull’immagine di quella linea. Di conseguenza, se due linee si incontrano in un punto, le loro immagini si incontrano nel punto corrispondente. Le relazioni di incidenza di punti e linee sono preservate per proiezione.
Una caratteristica importante che non si preserva affatto è la relazione di «parallelismo». Immaginate di trovarvi al centro di una lunga strada diritta e di guardare avanti. I due lati della strada, che nella realtà tridimensionale sono paralleli, e dunque non si incontrano mai, non appaiono paralleli, ma convergono verso un unico punto nel lontano orizzonte. Si comportano così su un piano ideale infinito, non soltanto su una Terra lievemente arrotondata. In effetti, si comportano esattamente in questo modo soltanto su un piano. Sopra una sfera, ci sarebbe un piccolo punto, troppo piccolo da vedere, dove le linee incontrano l’orizzonte. E tutta la questione delle rette parallele su una sfera è difficile comunque.
Questa caratteristica delle rette parallele è molto utile nei disegni prospettici, ed è alla base del modo consueto in cui disegniamo le scatole ad angolo retto in prospettiva, usando una linea di orizzonte e due punti che scompaiono, in corrispondenza della posizione in cui gli spigoli paralleli della scatola incontrano l’orizzonte in prospettiva. Piero della Francesca, nella sua opera De Prospettiva Pingendi (1482-87), applicò il metodo di Alberti nello sviluppo di alcune tecniche pratiche per gli artisti, e le usò con grande effetto nei suoi dipinti drammatici e molto realistici.
Gli scritti dei pittori del Rinascimento risolsero molti problemi nella geometria della prospettiva, ma erano semiempirici, e mancavano di un fondamento logico paragonabile a quello fornito da Euclide per la geometria ordinaria. Queste questioni fondamentali furono finalmente risolte da Brook Taylor e Johann Heinrich Lambert nel XVIII secolo. Allora però, la geometria aveva visto sviluppi più stimolanti.
Desargues
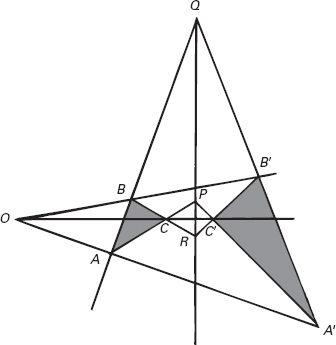
Il primo teorema non banale della geometria proiettiva fu concepito dall’ingegnere e architetto Girard Desargues, e fu pubblicato nel 1648 in un libro da Abraham Bosse. Desargues dimostrò il seguente importante teorema. Si supponga che i triangoli ABC e A′B′C′ siano in prospettiva, nel che i tre segmenti AA′, BB′, CC′ passano tutti attraverso lo stesso punto O. Allora i tre punti P, Q e R in cui si incontrano i lati corrispondenti dei due triangoli giacciono tutti sulla stessa linea. Oggi questo risultato è noto come teorema di Desargues. Non parla né di lunghezze né di angoli: riguarda soltanto le relazioni di incidenza tra linee e punti. È dunque un teorema proiettivo.
Esiste un trucco che rende il teorema ovvio: immaginatelo come il disegno di una figura tridimensionale, in cui i due triangoli giacciono in due piani. Allora la retta lungo cui questi piani si intersecano è la retta che contiene i tre punti di Desargues P, Q e R. Con una certa attenzione, il teorema si può anche dimostrare in questo modo, costruendo un’opportuna figura tridimensionale la cui proiezione appaia come i due triangoli. Possiamo quindi usare i metodi euclidei per dimostrare teoremi proiettivi.
Figura 12.1
Il teorema di Desargues.
Assiomi di Euclide
La geometria proiettiva differisce dalla geometria euclidea quando il suo punto di osservazione si allontana (gioco di parole), ma rimane sempre in relazione con la geometria euclidea. È lo studio di nuovi tipi di trasformazioni, proiezioni, ma il modello sottostante dello spazio in trasformazione è euclideo. Nonostante questo, la geometria proiettiva rese i matematici più ricettivi alla possibilità di un nuovo tipo di pensiero geometrico. E una vecchia questione, che era rimasta silente per secoli, venne ancora una volta alla ribalta.
Quasi tutti gli assiomi di Euclide per la geometria erano talmente ovvi che nessuna persona sana di mente avrebbe potuto metterli in discussione. Tutti gli angoli retti sono uguali, per esempio. Se quell’assioma non era valido, allora doveva esserci qualcosa di sbagliato nella definizione di angolo retto. Il quinto postulato invece, quello che riguardava proprio le rette parallele, aveva un carattere leggermente diverso: era complicato. Euclide lo enunciava in questo modo: se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, allora le due rette, se prolungate all’infinito, si incontreranno dalla parte in cui la somma dei due angoli è minore di due angoli retti.
Sembra più un teorema che un assioma. Era un teorema? Potrebbe esistere il modo di dimostrarlo, magari partendo da qualcosa di più semplice e più intuitivo?
Un passo avanti fu fatto da John Playfair nel 1795. Questi modificò l’enunciato dicendo che per ogni retta data, e ogni punto non appartenente a essa, esiste ed è unica una retta passante per il punto che è parallela alla retta data. Questo enunciato è equivalente in termini logici al quinto postulato di Euclide: vale a dire che uno è conseguenza dell’altro, dati gli altri assiomi.
Legendre
Nel 1794 Adrien-Marie Legendre scoprì un altro enunciato equivalente, l’esistenza di triangoli simili, cioè triangoli che hanno angoli uguali ma lati di dimensione diversa. Questi però, come anche la maggior parte degli altri matematici, cercava qualcosa di ancora più intuitivo. In effetti, la sensazione era che il quinto postulato fosse semplicemente superfluo, come una conseguenza degli altri assiomi. Tutto quello che serviva era una dimostrazione. Legendre tentò allora il tutto per tutto. Usando soltanto gli altri assiomi, dimostrò (in ogni caso con una certa soddisfazione personale) che la somma degli angoli interni di un triangolo è minore o uguale a 180°. (Legendre doveva sapere che nella geometria sferica la somma è maggiore, ma quella è la geometria della sfera e non del piano). Se la somma è sempre 180°, segue il quinto postulato. Egli suppose quindi che la somma potesse essere minore di 180° e derivò le implicazioni di quell’ipotesi.
Come incredibile conseguenza si otteneva una relazione tra l’area del triangolo e la somma dei suoi angoli. In particolare, l’area è proporzionale alla differenza tra 180° e la somma degli angoli. Questo risultato sembrava promettente: se fosse riuscito a costruire un triangolo con i lati doppi rispetto a quelli di un triangolo dato, ma con gli stessi angoli, allora avrebbe ottenuto una contraddizione, perché il triangolo maggiore non avrebbe avuto la stessa area del minore. Comunque tentasse di costruire il triangolo più grande, si trovava però a far ricorso al quinto postulato.
Da questo lavoro riuscì a salvare un risultato positivo. Senza assumere il quinto postulato, dimostrò che per alcuni triangoli la somma degli angoli interni non può mai essere maggiore di 180°, mentre per altri la somma è minore di 180°. Se la somma degli angoli interni di un triangolo supera 180°, allora lo stesso vale per ogni triangolo; lo stesso vale se la somma è minore di 180°. Si verificano quindi tre casi possibili:
– la somma degli angoli interni di ogni triangolo è esattamente 180° (geometria euclidea);
– la somma degli angoli interni di ogni triangolo è minore di 180°;
– la somma degli angoli interni di ogni triangolo è maggiore di 180° (un caso che Legendre pensava di aver escluso; si scoprì in seguito che per farlo aveva considerato altre ipotesi non dette).
Saccheri
Nel 1733 Gerolamo Saccheri, un padre gesuita di Pavia, pubblicò un’opera eroica, Euclides ab omni naevo vindicatus. Anch’egli considerò tre casi, dei quali il primo era la geometria euclidea, ma usò un quadrilatero per operare la distinzione. Supponiamo che il quadrilatero sia ABCD, con A e B angoli retti e AC = BD. Allora, affermava Saccheri, la geometria euclidea implica che gli angoli C e D siano retti. In maniera meno ovvia, se C e D sono angoli retti in un quadrilatero di questo tipo, allora segue il quinto postulato.
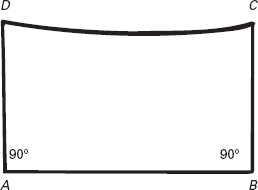
Figura 12.2
Il quadrilatero di Saccheri: il segmento CD deve essere tracciato curvo per aggirare le ipotesi euclidee sugli angoli C e D.
Senza usare il quinto postulato, Saccheri dimostrò che gli angoli C e D sono uguali. Questo lasciava quindi aperte due distinte possibilità:
– ipotesi dell’angolo ottuso: sia C che D sono maggiori di un angolo retto;
– ipotesi dell’angolo acuto: sia C che D sono minori di un angolo retto.
L’idea di Saccheri era assumere una alla volta ognuna di queste ipotesi, per dedurre una contraddizione logica, che avrebbe condotto alla geometria euclidea come unica possibilità logica.
Saccheri iniziò con l’ipotesi dell’angolo ottuso, e in una serie di teoremi dedusse (così egli pensava) che gli angoli C e D dovessero di fatto essere comunque rettangoli. Questa era una contraddizione, e dunque l’ipotesi dell’angolo ottuso doveva essere falsa. Assunse poi l’ipotesi dell’angolo acuto, che condusse a un’altra serie di teoremi, tutti corretti, e abbastanza interessanti di per sé. Alla fine dimostrò un teorema piuttosto complicato su una famiglia di rette tutte passanti attraverso un punto, il quale implicava che due di queste rette avessero una perpendicolare comune all’infinito. Questa non è in realtà una contraddizione, ma Saccheri pensava che lo fosse e dichiarò che anche l’ipotesi dell’angolo acuto dovesse essere scartata.
Tutto questo lasciava soltanto la geometria euclidea, e dunque Saccheri pensò che il suo programma fosse stato soddisfatto, insieme con Euclide. Altri però notarono che egli non aveva in realtà ottenuto una contraddizione dall’ipotesi dell’angolo acuto: soltanto un teorema piuttosto sorprendente. Nel 1759 d’Alembert definì il quinto postulato «lo scandalo degli elementi di geometria».
Quello che la geometria non euclidea fece per loro
Nel 1813 Gauss si stava sempre più convincendo che quella che in principio chiamava geometria anti-euclidea, poi astrale e infine non euclidea era una possibilità logica. Cominciò a chiedersi quale fosse la vera geometria dello spazio, e misurò gli angoli di un triangolo che ha come vertici le cime di tre monti vicino a Göttingen: Hohenhagen, Brocken e Inselberg. Effettuò le misurazioni lungo la linea di visibilità (lungo l’asse LOS, line of sight, in termini tecnici) in modo da poter trascurare la curvatura della Terra. La somma degli angoli misurati era 15 secondi di arco maggiore di 180°. Se non altro, questo era il caso dell’angolo ottuso, ma la probabilità di errori di misurazione rese discutibile tutto l’esercizio. Gauss aveva bisogno di un triangolo molto più grande, e di strumenti molto più accurati per misurarne gli angoli.
Lambert
Un matematico tedesco, Georg Klügel, lesse il libro di Saccheri, ed espose l’opinione non ortodossa e piuttosto sconvolgente che credere nella verità del quinto postulato era una questione di esperienza piuttosto che di logica. In sostanza, egli diceva che qualcosa nel nostro modo di pensare allo spazio ci fa credere nell’esistenza di rette parallele del tipo immaginato da Euclide.
Nel 1766, Johann Heinrich Lambert, seguendo il suggerimento di Klügel, intraprese una ricerca simile a quella di Saccheri, prendendo però avvio da un quadrilatero con tre angoli retti. L’angolo rimanente doveva essere retto (geometria euclidea), acuto oppure ottuso. Come Saccheri, Lambert pensava che il caso dell’angolo ottuso conducesse a una contraddizione. Più precisamente, concluse che portava alla geometria sferica, nella quale si sapeva da tempo che la somma degli angoli di un triangolo supera 180°. Dal momento che la sfera non è il piano, il caso ottuso era scartato.
In ogni caso, non affermò lo stesso nel caso dell’angolo acuto. Al contrario, dimostrò alcuni curiosi teoremi, il più particolare dei quali è una formula per l’area di un poligono con n lati. Si sommino tutti gli angoli, e si sottragga questo valore da 2n − 4 angoli retti: il risultato è proporzionale all’area del poligono. Questa formula ne ricordò a Lambert una simile per la geometria sferica: si sommino tutti gli angoli, e si sottraggano 2n − 4 angoli retti da questo valore: di nuovo il risultato è proporzionale all’area del poligono. La differenza è minima: la sottrazione è effettuata nell’ordine opposto. Lambert fu portato a formulare una previsione particolarmente profetica ma oscura: la geometria del caso dell’angolo acuto è uguale a quella su una sfera con raggio immaginario.
Lambert scrisse allora un breve articolo sulle funzioni trigonometriche di angoli immaginari, ottenendo alcune belle formule assolutamente consistenti. Noi ora conosciamo queste funzioni con il nome di funzioni iperboliche, che possono essere definite senza usare i numeri immaginari, e soddisfano tutte le formule di Lambert. Chiaramente qualcosa di interessante deve esserci sotto questa curiosa, enigmatica ipotesi. Ma che cosa?
Il dilemma di Gauss
A questo punto i geometri più preparati si stavano convincendo che il quinto postulato di Euclide non potesse essere dimostrato a partire dagli altri assiomi. Il caso dell’angolo acuto sembrava troppo autocoerente per portare a una contraddizione. D’altra parte, una sfera di raggio immaginario non era il tipo di oggetto che poteva essere proposto per giustificare quella convinzione.
Uno di questi geometri era Gauss, che si era convinto da molto tempo che una geometria non euclidea logicamente coerente fosse possibile, e dimostrò numerosi teoremi nel contesto di questa geometria. Come però rese chiaro nel 1829 in una lettera a Bessel, non aveva alcuna intenzione di pubblicare parte di questo lavoro, perché temeva quelle che egli definiva le «strida dei beoti». Le persone prive di immaginazione non avrebbero capito, e nella loro ignoranza sostenuta dalla rigida fedeltà alla tradizione, avrebbero messo alla berlina il suo lavoro. In questo Gauss aveva forse subito l’influenza dell’eccelsa notorietà del celeberrimo lavoro filosofico di Kant: questi aveva sostenuto che la geometria dello spazio doveva essere euclidea.
Nel 1799, Gauss scriveva all’amico ungherese Wolfgang Bolyai, informandolo che la ricerca «sembra piuttosto indurmi a dubitare della verità della geometria stessa. È vero che ho raggiunto molti risultati che la maggioranza delle persone direbbe che costituiscono una dimostrazione [della deducibilità del quinto postulato dagli altri assiomi]; ma ai miei occhi non dimostrano proprio niente».
Altri matematici furono meno circospetti. Nel 1826 Nikolaj Ivanovič Lobačevskij, all’Università di Kazan in Russia, tenne alcune lezioni sulla geometria non euclidea. Non era a conoscenza del lavoro di Gauss, ma aveva dimostrato teoremi simili usando metodi propri. Due articoli sull’argomento apparvero nel 1829 e nel 1835. Piuttosto che sollevare clamore, come Gauss aveva temuto, questi articoli caddero nell’oblio senza lasciare traccia. Nel 1840 Lobačevskij stava pubblicando un libro sull’argomento, in cui lamentava la mancanza di interesse. Nel 1855 pubblicò un altro libro sull’argomento.
In maniera indipendente, il figlio di Wolfgang Bolyai, János, ufficiale dell’esercito, intorno al 1825 espose alcune idee simili, in un articolo di ventisei pagine che fu pubblicato come appendice all’opera di geometria del padre Tentamen juventum studiosam in elementa matheseos, apparsa nel 1832. «Ho fatto scoperte talmente meravigliose da rimanerne sbalordito anch’io», scrisse János al padre.
Gauss lesse il lavoro, ma spiegò a Wolfgang che non poteva lodare gli sforzi del giovane senza elogiare se stesso. L’atteggiamento di Gauss fu forse poco cortese, ma il grande matematico era solito comportarsi in questo modo.
Geometria non euclidea
La storia della geometria non euclidea è troppo complicata per descriverla nei minimi dettagli, ma possiamo riassumere che cosa venne dopo questi sforzi pionieristici. C’è un’unità di fondo nei tre casi individuati da Saccheri, da Lambert e da Gauss, Bolyai e Lobačevskij. Quello che li unisce è il concetto di curvatura. La geometria non euclidea è davvero la geometria naturale di una superficie curva.
Se la superficie ha curvatura positiva come una sfera, allora abbiamo il caso dell’angolo ottuso. Questo fu scartato perché la geometria sferica differisce da quella euclidea in maniera ovvia: per esempio, due linee qualsiasi, cioè circonferenze massime (i cui centri si trovano al centro della sfera) si incontrano in due punti, non in uno come ci aspettiamo con due rette dritte euclidee.
In realtà, comprendiamo ora che questa obiezione è priva di fondamento. Se identifichiamo punti diametralmente opposti della sfera (supponiamo cioè che siano identici) allora le linee (circonferenze massime) hanno ancora senso, perché se un punto giace su una circonferenza massima, lo stesso farà il punto diametralmente opposto. Con questa identificazione, quasi tutte le proprietà geometriche rimangono invariate, ma ora le rette si incontrano in un solo punto.
Dal punto di vista della topologia, la superficie che si ottiene è il piano proiettivo, anche se la geometria implicata non è la geometria proiettiva ortodossa. Ora la chiamiamo geometria ellittica, e la consideriamo ragionevole come quella euclidea.
Se la superficie ha curvatura negativa, come una sella, allora abbiamo il caso dell’angolo acuto. La geometria che ne risulta è chiamata iperbolica. Presenta diverse caratteristiche interessanti, che la distinguono dalla geometria euclidea.
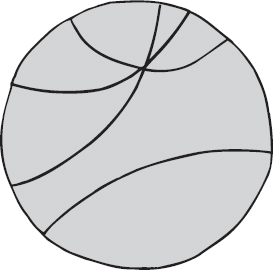
Figura 12.3
Il modello di Poincaré di una geometria iperbolica rende chiaro che esiste un numero infinito di rette parallele che passano per un punto che non interseca una data retta.
Quello che la geometria non euclidea fa per noi
Che forma ha l’universo? La domanda può sembrare semplice ma rispondere è difficile, intanto perché l’universo è immenso, ma soprattutto perché noi ci siamo dentro e non possiamo fare un passo indietro per osservarlo nella sua integrità. Per usare un’analogia che risale a Gauss, una formica che vive su una superficie, osservandola soltanto da quella prospettiva, non è in grado di dire facilmente se la superficie è un piano, una sfera, un toro o qualcosa di più complicato.
La relatività generale dice che vicino a un corpo materiale, come una stella, lo spazio-tempo è curvo. Le equazioni di Einstein, che mettono in relazione la curvatura con la densità di materia, hanno molte soluzioni differenti. Nelle più semplici, l’universo nel suo complesso ha curvatura positiva e di conseguenza ha la topologia di una sfera. Per quanto possiamo dire però, la curvatura complessiva dell’universo reale potrebbe invece essere negativa. Non sappiamo neppure se l’universo è infinito, come lo spazio euclideo, o se ha dimensione finita, come una sfera. Alcuni fisici sostengono che l’universo sia infinito, ma il supporto sperimentale offerto all’ipotesi è grandemente opinabile. La maggior parte degli scienziati sostiene che l’universo sia finito.
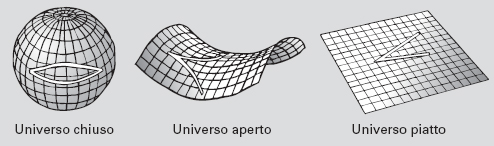
Spazio con curvatura positiva, negativa e nulla.
Un universo chiuso si curva su se stesso. Le rette che sarebbero divergenti si incontrano. La densità è maggiore della densità critica.
Un universo aperto si curva allontanandosi da se stesso. Le rette divergenti si allontanano l’una dall’altra con un angolo crescente. La densità è minore della densità critica.
Un universo piatto non ha curvatura. Le rette divergenti mantengono un angolo costante l’una rispetto all’altra. La densità è pari alla densità critica.
Stranamente, un universo finito può esistere senza avere un confine. La sfera è come quella in due dimensioni, e lo stesso vale per il toro. Il toro può essere dotato di una geometria piatta, derivata da un quadrato identificando i lati opposti. Gli studiosi di topologia hanno anche scoperto che lo spazio può essere finito ma con curvatura negativa: un modo per costruire spazi del genere è prendere un poliedro finito nello spazio iperbolico e identificare, cioè «incollare» insieme facce diverse, in modo che una retta che esce dal poliedro in una faccia rientri immediatamente in un’altra faccia (un po’ quello che succede in molti videogame quando un oggetto esce da un bordo dello schermo per rientrare istantaneamente dall’altro).
Se lo spazio è finito, allora dovrebbe essere possibile osservare la stessa stella in direzioni diverse, anche se potrebbe sembrare molto più lontana in certe direzioni rispetto ad altre, e la regione osservabile dell’universo potrebbe essere comunque troppo piccola. Se uno spazio finito ha una geometria iperbolica, queste diverse osservazioni della stessa stella in direzioni diverse determinano nei cieli un sistema di gigantesche circonferenze, e la geometria di quelle circonferenze determina qual è lo spazio iperbolico osservato. Le circonferenze potrebbero però essere ovunque tra i miliardi di stelle osservabili, e finora tutti i tentativi di osservarle, basati su correlazioni statistiche tra le posizioni apparenti delle stelle, non hanno fornito alcun risultato.
Nel 2003 i dati provenienti dalla sonda anisotropa a microonde Wilkinson (Wilkinson microwave anisotropy probe, WMAP) hanno indotto Jean-Pierre Luminet e i suoi collaboratori a supporre che lo spazio sia finito ma con curvatura positiva. Questi ricercatori hanno trovato che lo spazio dodecaedrico di Poincaré – ottenuto identificando le facce opposte di un dodecaedro curvo – fornisce il miglior accordo con le osservazioni. Questa ipotesi non è stata confermata, e ad oggi non abbiamo idea di quale sia la vera forma dello spazio. Ad ogni modo, abbiamo capito molto meglio che cosa dovremmo fare per trovarla.
Per ottenere lo spazio dodecaedrico di Poincaré, si identifica ogni faccia con quella opposta.
Se la superficie ha curvatura nulla, come un piano euclideo, allora è il piano euclideo, e otteniamo la geometria euclidea.
Tutte e tre le geometrie soddisfano tutti gli assiomi di Euclide tranne il quinto postulato. La decisione di Euclide di includere il suo postulato è giustificata.
Queste diverse geometrie possono essere modellate in modi differenti. La geometria iperbolica è particolarmente versatile sotto questo aspetto. In un modello lo spazio coinvolto è la metà superiore del piano complesso, tralasciando l’asse reale e tutto quello che sta sotto. Una linea è una semicirconferenza che interseca l’asse reale ad angoli retti. Dal punto di vista della topologia, questo spazio è uguale a un piano, e le linee sono identiche a rette ordinarie. La curvatura delle linee riflette la curvatura negativa dello spazio sottostante.
In un secondo modello della geometria iperbolica, introdotto da Poincaré, lo spazio è rappresentato come l’interno di un cerchio, senza includere il contorno, e le linee sono circonferenze che intersecano il contorno ad angoli retti. Anche in questo caso la geometria distorta riflette la curvatura dello spazio sottostante. L’artista Maurits Escher ha realizzato diverse opere basandosi su questo modello di geometria iperbolica, che aveva imparato dallo studioso di geometria canadese Coxeter.
I due modelli suggeriscono qualche profonda relazione tra la geometria iperbolica e l’analisi complessa. Questi collegamenti si riferiscono a certi gruppi di trasformazioni del piano complesso; la geometria iperbolica è la geometria dei loro invarianti, in accordo con il programma di Erlangen di Felix Klein. Un’altra classe di trasformazioni, chiamate trasformazioni di Möbius, chiama in gioco anche la geometria ellittica.
La geometria dello spazio
Che dire della geometria dello spazio? Noi ora concordiamo con Klügel, e abbiamo abbandonato Kant. È una questione di esperienza, non qualcosa che si può dedurre soltanto con il pensiero. La relatività generale di Einstein ci dice che lo spazio (e il tempo) può essere curvo: la curvatura è l’effetto gravitazionale della materia. La curvatura può variare da una posizione all’altra, a seconda del modo in cui è distribuita la materia. La vera questione non è quindi la geometria dello spazio. Lo spazio può avere differenti geometrie in luoghi differenti. La geometria di Euclide funziona bene alla scala umana, nel mondo umano, perché la curvatura gravitazionale è talmente piccola che non la osserviamo nel quotidiano. Là fuori però, nell’universo più grande, prevalgono geometrie non euclidee.
Per gli antichi e per buona parte del XIX secolo, la matematica e il mondo reale erano disperatamente confusi. C’era la convinzione generale che la matematica fosse una rappresentazione di caratteristiche fondamentali e inevitabili del mondo reale, e che la verità matematica fosse assoluta. E questa ipotesi era radicata profondamente soprattutto nella geometria classica. Lo spazio era euclideo, per quasi tutti quelli che avevano riflettuto sulla questione. Che altro poteva essere?
Questo problema cessò di essere retorico quando cominciarono ad affacciarsi alcune alternative alla geometria di Euclide, consistenti dal punto di vista logico. Ci volle tempo per riconoscere che erano consistenti dal punto di vista logico – almeno consistenti quanto la geometria di Euclide – e un tempo ancora più lungo per comprendere che il nostro spazio fisico può non essere perfettamente euclideo. Come sempre, la colpa fu del provincialismo umano: stavamo proiettando nell’universo globale le nostre limitate esperienze raccolte in un angolino dell’universo. La nostra fantasia sembra preferire un modello euclideo, forse perché, sulla piccola scala della nostra esperienza, è un modello eccellente e anche il più semplice disponibile.
Grazie alle idee di alcuni personaggi lungimiranti e non ortodossi, spesso violentemente avversati da una maggioranza meno lungimirante, è ora accettato – almeno da matematici e fisici – che esistono alternative diverse alla geometria di Euclide, e che la natura dello spazio fisico è una questione di osservazione, non di pensiero puro. Facciamo ora una chiara distinzione tra i modelli matematici della realtà, e la realtà stessa. Per inciso, gran parte della matematica non ha alcuna relazione ovvia con la realtà, ma è utile, comunque.