17.

La forma della logica

Porre la matematica su fondamenta abbastanza salde

Mentre la superstruttura della matematica cresceva sempre più, un piccolo numero di matematici cominciò a chiedersi se le fondamenta potessero reggerne il peso. Le diverse crisi dei fondamenti della matematica, in particolare la controversia sui concetti di base del calcolo infinitesimale e la generale confusione sulle serie di Fourier, avevano chiarito la necessità di definire i concetti matematici in maniera molto accurata e precisa allo scopo di evitare trappole logiche. Le torri di deduzione della materia avrebbero altrimenti potuto collassare con facilità in contraddizioni logiche, a causa di qualche imprecisione o ambiguità di base.

In un primo tempo, le preoccupazioni di questo genere si concentravano su idee complicate e sofisticate, come la serie di Fourier. Lentamente però il mondo matematico giunse a comprendere che anche principi molto elementari potevano essere messi in dubbio, e primo tra tutti il concetto di numero. La terribile verità era che i matematici si erano concentrati con tanta passione sulla scoperta di proprietà particolari dei numeri che avevano tralasciato di chiedersi che cosa erano i numeri. E quando venne il momento di proporre una definizione logica, non lo sapevano.

Dedekind

Nel 1858, docente di un corso di analisi infinitesimale, Dedekind cominciò a interrogarsi sui fondamenti dell’analisi, e non sull’uso dei limiti, ma sul sistema dei numeri reali. Pubblicò i suoi pensieri nel 1872 nel lavoro Stetigkeit und irrationale Zahlen, sottolineando come proprietà in apparenza ovvie dei numeri reali non fossero mai state dimostrate in alcuna maniera rigorosa. A titolo di esempio citava l’equazione 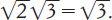Questo risultato, com’è ovvio, seguiva applicando la funzione quadrato a entrambi i membri dell’equazione, peccato però che la moltiplicazione di numeri irrazionali non fosse stata mai definita. Nel suo libro del 1888 Was sind und was sollen die Zahlen? evidenziò serie lacune insite nei fondamenti logici del sistema dei numeri reali. Nessuno aveva davvero dimostrato che i numeri reali esistono.

Propose anche una maniera per colmare queste lacune, introducendo quelli che ora chiamiamo tagli di Dedekind. L’idea era di partire da un sistema numerico accettato, i numeri razionali, ed estenderlo, per ottenere il sistema più ricco dei numeri reali. La sua impostazione prendeva in esame le proprietà richieste dei numeri reali, trovava il modo di riformularle soltanto in termini dei numeri razionali e poi invertiva il procedimento, interpretando quelle caratteristiche dei numeri razionali come una definizione dei reali. Questo tipo di ingegneria inversa per formulare nuovi concetti a partire dai vecchi è stato da allora ampiamente usato.

Supponiamo, per il momento, che i numeri reali esistano. Che relazione hanno con i numeri razionali? Alcuni reali non sono razionali, e un esempio ovvio è 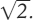Ora, anche se non è una frazione esatta, il valore può essere approssimato dai razionali con la precisione voluta. Si colloca da qualche parte in una posizione specifica, infilato nella fitta schiera dei possibili razionali. Ora però come possiamo determinare quella posizione? Dedekind comprese che 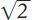separa nettamente l’insieme dei numeri razionali in due parti: quelli che sono minori di 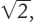e quelli che sono maggiori. In un certo senso, questa separazione − o taglio − definisce il numero 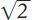in termini dei razionali. L’unico problema è che usiamo 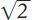per definire le due parti del taglio. Esiste però una via di uscita. I numeri razionali maggiori di 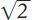sono esattamente quelli positivi, per i quali il quadrato è maggiore di 2. I numeri razionali minori di 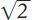sono tutti gli altri. Questi due insiemi di numeri razionali sono ora definiti senza alcun ricorso esplicito a 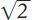, ma ne specificano esattamente la posizione sulla retta dei numeri reali.

Dedekind dimostrò che se ipotizziamo, a titolo di esempio, che i numeri reali esistano, allora possiamo associare a qualunque numero reale un taglio che soddisfi queste due proprietà, formando due insiemi: l’insieme D di tutti i razionali maggiori di quel numero reale, e l’insieme S di tutti i razionali minori di quel numero reale, o uguali ad esso. (La condizione finale è necessaria per associare un taglio a ogni numero razionale: non vogliamo trascurarne nessuno). Qui S e D possono essere letti come sinistra e destra nella consueta rappresentazione della retta dei numeri reali.

Questi due insiemi S e D soddisfano alcune condizioni piuttosto severe. In primo luogo, ogni numero razionale appartiene esattamente a uno dei due. Secondo, ogni numero in D è maggiore di ogni numero in S. Infine, esiste una condizione tecnica che tiene conto dei numeri razionali in quanto tali: S può avere un massimo oppure no, ma D non ha mai un minimo. Ogni coppia di sottoinsiemi dei razionali con queste proprietà è definita come un taglio.

Nell’ingegneria inversa, non abbiamo bisogno di assumere che i numeri reali esistano. Al contrario, possiamo usare tagli per definire i numeri reali, tanto che di fatto un numero reale è un taglio. In genere non pensiamo a un numero reale in questo modo, ma Dedekind comprese che se vogliamo lo possiamo fare. La difficoltà principale è definire come sommare e moltiplicare tagli, in modo che l’aritmetica dei numeri reali abbia un senso, e questo si rivela facile. Per sommare due tagli (S₁, D₁) e (S₂, D₂), definiamo S₁ + S₂ come l’insieme di tutti i numeri ottenibili sommando un numero in S₁ a un numero in S₂, e in maniera analoga definiamo D₁ + D₂. Allora la somma di questi due tagli è il taglio (S₁ + S₂, D₁ + D₂). La moltiplicazione è simile, ma numeri positivi e negativi si comportano in maniera leggermente diversa.

Infine, dobbiamo verificare che l’aritmetica dei tagli abbia tutte le caratteristiche dei numeri reali che ci aspettiamo. Queste includono le leggi ordinarie dell’algebra, che seguono tutte da analoghe caratteristiche dei numeri razionali. La caratteristica fondamentale, che distingue i reali dai razionali, è che il limite di una successione infinita di tagli esiste (sotto certe condizioni tecniche). In maniera equivalente, esiste un taglio in corrispondenza di qualunque espansione decimale infinita (anche questo è abbastanza semplice).

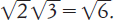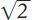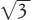Assumendo che tutto questo sia possibile, vediamo dunque come Dedekind può dimostrare che Abbiamo visto che corrisponde al taglio (S₁, D₁) dove D₁ è formato da tutti i razionali positivi il cui quadrato è maggiore di 2. In maniera simile, corrisponde al taglio (S₂, D₂) dove D₂ è formato da tutti i razionali positivi il cui quadrato è maggiore di 3. Si dimostra facilmente che il prodotto di questi tagli è (S₃, D₃) dove D₃ è formato da tutti i razionali positivi il cui quadrato è maggiore di 6. Questo taglio corrisponde però a Fatto!

La bellezza dell’impostazione di Dedekind consiste nel ridurre tutte le questioni riguardanti i numeri reali a questioni corrispondenti sui numeri razionali, e nello specifico, su coppie di insiemi di numeri razionali. Definisce pertanto i numeri reali soltanto in termini di numeri razionali e operazioni su quei numeri. Il risultato è che i numeri reali esistono (in termini matematici) a patto che esistano i numeri razionali.

C’è un piccolo prezzo da pagare: un numero reale è ora definito come una coppia di insiemi di razionali, e questo non è la maniera consueta con cui pensiamo a un numero reale. Se questo suona bizzarro, tenete a mente che la rappresentazione abituale di un numero reale come decimale infinito richiede una successione infinita di cifre decimali 0-9. Questo è concettualmente complicato tanto quanto un taglio di Dedekind. È in realtà molto macchinoso definire la somma o il prodotto di due decimali infiniti, perché i metodi aritmetici tradizionali per sommare o moltiplicare decimali si applicano a partire dall’estremità destra, e quando un decimale è infinito non ha un’estremità destra.

Assiomi per numeri interi

L’opera di Dedekind era ottima come esercizio sui fondamenti, ma quando il punto generale circa la definizione dei termini decadde, fu presto chiaro che il libro aveva semplicemente spostato l’attenzione dai reali ai razionali. Come facciamo a sapere che i numeri razionali esistono? Certo, se assumiamo che gli interi esistano, allora è facile: definiamo un razionale p/q come una coppia di interi (p, q) e calcoliamo le formule per somma e prodotto. Se gli interi esistono, lo stesso vale per le coppie di interi.

Sì, ma come sappiamo che gli interi esistono? A parte il segno più o meno, gli interi sono comuni numeri naturali. Tener conto del segno è facile, e dunque gli interi esistono a patto che i numeri naturali esistano.

Non abbiamo ancora finito però. Siamo talmente abituati ai numeri naturali che non ci capita mai di domandarci se i familiari numeri 0, 1, 2, 3 e così via esistono davvero. E se esistono, che cosa sono?

Nel 1889, Giuseppe Peano eluse la questione sull’esistenza prendendo esempio dal libro di Euclide. Invece di discutere l’esistenza di punti, rette, triangoli e similari, Euclide semplicemente stilò un elenco di assiomi, cioè proprietà da assumere senza ulteriori domande. Non importa se punti e compagnia bella esistono, mentre una questione più interessante è: se esistono, quali proprietà seguono? Peano scrisse quindi un elenco di assiomi per i numeri naturali. Le caratteristiche principali erano:

– esiste un numero 0;

– ogni numero n ha un successore, s(n) (che pensiamo come n + 1);

– se P(n) è una proprietà dei numeri, tale che P(0) è vera, e ogni volta che P(n) è vera allora P(s(n)) è vera, allora P(n) è vera per ogni n (principio dell’induzione matematica).

Peano definì quindi i numeri 1, 2 ecc. in termini di questi assiomi, ponendo di fatto

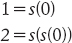
e così via. Definì anche le operazioni fondamentali dell’aritmetica e dimostrò che obbediscono alle leggi consuete. Nel suo sistema, 2 + 2 = 4 è un teorema dimostrabile, enunciato come s(s(0)) + s(s(0)) = s(s(s(s(0)))).

Questa impostazione assiomatica offre un grande vantaggio perché si focalizza esattamente su quello che dobbiamo provare se vogliamo mostrare, con un mezzo o con l’altro, che i numeri naturali esistono. Dobbiamo soltanto costruire un sistema che soddisfi tutti gli assiomi di Peano.

Il concetto fondamentale a questo punto è il significato di «esistenza» in matematica. Nel mondo reale, qualcosa esiste se possiamo osservarlo, o in alternativa, dedurre la sua necessaria presenza da cose che possono essere osservate. Noi sappiamo che la gravità esiste perché possiamo osservarne gli effetti, anche se nessuno può vedere la gravità. Nel mondo reale, dunque, possiamo ragionevolmente parlare dell’esistenza di due gatti, due biciclette o due panini. In ogni caso, il numero due è un’altra cosa. Non è un oggetto, ma un artefatto concettuale. Non incontriamo mai il numero due nel mondo reale. Ci possiamo al più avvicinare a un simbolo, 2, scritto o stampato su carta, o visualizzato sullo schermo del computer. Nessuno però crede che un simbolo sia equivalente alla cosa che esso rappresenta. La parola «gatto» scritta con l’inchiostro non è un gatto. Analogamente, il simbolo 2 non è il numero due.

Il significato di «numero» è un problema concettuale e filosofico sorprendentemente complicato. Tutto è reso più disastroso dal fatto che noi tutti sappiamo benissimo come usare i numeri. Sappiamo come si comportano, ma non sappiamo che cosa sono.

Insiemi e classi

Intorno al 1880 Gottlob Frege tentò di risolvere questo problema concettuale costruendo i numeri naturali a partire da oggetti più semplici, tipo insiemi, o classi come li chiamava. Il suo punto di partenza fu l’associazione tradizionale dei numeri con l’azione del contare. Secondo Frege, due è una proprietà di quegli insiemi, e soltanto di quelli, che possono essere messi in corrispondenza biunivoca con un insieme standard {a, b} formato da due membri distinti a e b. Di conseguenza gli insiemi

possono tutti avere una corrispondenza con {a, b}, e dunque determinano tutti, qualunque cosa questo significhi, lo stesso numero.

Purtroppo, l’uso di un elenco di insiemi tipo come numeri porta a presupporre di aver già risolto la questione: è proprio come confondere un simbolo con quello che esso rappresenta. Come possiamo però caratterizzare «una proprietà di quegli insiemi che possono essere messi in corrispondenza biunivoca con un insieme tipo»? Che cos’è una proprietà? Frege ebbe una meravigliosa intuizione. Esiste un insieme ben definito che è associato con qualunque proprietà: di fatto, l’insieme che consiste di tutto quello che possiede quella proprietà. La proprietà «primo» è associata con l’insieme di tutti i numeri primi; la proprietà «isoscele» è associata con l’insieme di tutti i triangoli isosceli, e così via.

Frege ipotizzò così che il numero due è l’insieme formato da tutti gli insiemi che possono essere messi in corrispondenza biunivoca con l’insieme tipo {a, b}. In termini più generali, un numero è l’insieme di tutti gli insiemi che possono essere messi in corrispondenza con ogni insieme dato. Per esempio allora il numero 3 è l’insieme

anche se probabilmente è meglio usare oggetti matematici al posto di gatti o lettere.

Con queste premesse, Frege scoprì di poter fondare su una base logica l’intero corpus aritmetico dei numeri naturali. Tutto si riduceva a proprietà ovvie degli insiemi. Espose il risultato nel suo capolavoro del 1884 Die Grundlagen der Arithmetik, ma con suo grande disappunto Georg Cantor, un eminente logico matematico, liquidò il libro come opera di nessun valore. Nel 1893 Frege, intrepido, pubblicò il primo volume di un altro libro, Die Grundgesetze der Arithmetik, nel quale introduceva un sistema intuitivo e convincente di assiomi per l’aritmetica. Peano lo recensì, mentre tutti gli altri lo ignorarono. Dieci anni dopo, Frege era finalmente pronto per la pubblicazione del secondo volume, ma a quel tempo aveva individuato nei suoi assiomi una lacuna di fondo, che anche altri avevano notato. Mentre il secondo volume era in stampa, accadde il fattaccio. Frege ricevette una lettera da parte del filosofo matematico Bertrand Russell, al quale egli aveva inviato le bozze finali del libro. Per parafrasare, la lettera diceva a grandi linee così: «Caro Gottlob, considera l’insieme di tutti gli insiemi che non sono membri di se stessi. Tuo, Bertrand».

Frege era un ottimo logico e immediatamente comprese l’appunto di Russell: di fatto egli era già conscio delle potenziali difficoltà. Tutta l’impostazione di Frege supponeva, senza dimostrarlo, che qualunque proprietà ragionevole definisse un insieme sensato, formato da quegli oggetti che possiedono la proprietà considerata. Qui c’era però una proprietà apparentemente ragionevole, non essere membro di se stesso, che chiaramente non corrispondeva ad alcun insieme.

Uno sconsolato Frege aggiunse un’appendice alla sua opera magna, discutendo l’obiezione di Russell. Ideò un veloce espediente: eliminare dal regno degli insiemi tutti quelli che sono membri di se stessi. Questo stratagemma comunque non lo soddisfò mai pienamente.

Russell, da parte sua, tentò di colmare la lacuna nella costruzione dei numeri naturali operata da Frege a partire dagli insiemi. La sua idea era di limitare il tipo di proprietà che poteva essere usata per definire un insieme. Naturalmente doveva trovare una dimostrazione del fatto che questo tipo limitato di proprietà non conducesse in alcun caso a un paradosso. In collaborazione con Alfred North Whitehead, pervenne a una complicata e tecnica teoria dei tipi che faceva allo scopo, almeno per la loro personale soddisfazione. Esposero il loro metodo in una corposa opera in tre volumi, i Principia mathematica, pubblicata tra il 1910 e il 1913. La definizione del numero 2 si trova quasi alla fine del primo volume, e il teorema 1 + 1 = 2 è dimostrato a pagina 86 del secondo volume. In ogni caso, i Principia mathematica non posero fine al dibattito sui fondamenti. Anche la teoria dei tipi era controversa. I matematici erano alla ricerca di qualcosa di più semplice e più intuitivo.

Cantor

Questi studi sul ruolo fondamentale della computazione come base per i numeri condussero a una delle più audaci scoperte di tutta la matematica: la teoria di Cantor dei numeri transfiniti, con la quale si introduceva il concetto di differenti dimensioni di infinito.

L’infinito, per diversi aspetti, sembra inevitabile in matematica. Non esiste un numero naturale massimo, perché aggiungendo un’unità otteniamo sempre un numero maggiore, e dunque i numeri naturali sono infiniti. Euclide applicò la sua geometria su un piano infinito, e dimostrò che esiste un numero infinito di primi. Nel periodo che precedette l’introduzione del calcolo infinitesimale, molti matematici, e tra questi Archimede, trovarono utile pensare a un’area o a un volume come alla somma di un numero infinito di porzioni infinitamente piccole. Nel periodo che seguì lo sviluppo del calcolo infinitesimale, la stessa concezione di aree e volumi era usata per scopi euristici, anche se le dimostrazioni erano condotte ormai in maniera diversa.

Queste manifestazioni dell’infinito potrebbero essere riformulate in termini finiti per evitare molte difficoltà filosofiche. Invece di dire «i numeri naturali sono infiniti», per esempio, potremmo invece affermare «non esiste un numero naturale massimo». La seconda affermazione evita un’esplicita introduzione dell’infinito, per quanto in termini logici sia equivalente alla prima. Di fatto, l’infinito è qui pensato come un processo, che può essere portato avanti senza alcun limite particolare, ma non è mai davvero completato. I filosofi definiscono come infinito potenziale questo tipo di infinito. Diversamente, l’uso esplicito dell’infinito come oggetto matematico in quanto tale è davvero infinito.

I matematici prima di Cantor avevano notato che gli infiniti reali avevano caratteristiche paradossali. Nel 1632 Galileo scrisse il suo Dialogo sopra i due massimi sistemi del mondo, in cui due personaggi di fantasia, il sagace Salviati e Sagredo, un laico intelligente, discutono le cause delle maree, dal punto di vista geocentrico ed eliocentrico. Ogni riferimento alle maree fu cancellato su richiesta delle autorità ecclesiastiche, rendendo il libro un esercizio ipotetico che nondimeno rese una forte testimonianza a favore della teoria eliocentrica di Copernico. Nel corso del dialogo, i due personaggi discutono alcuni dei paradossi dell’infinito. Salviati domanda se «i numeri sono più dei quadrati?», e osserva che dal momento che i numeri naturali per la maggior parte non sono quadrati perfetti, la risposta deve essere affermativa. Aggiunge poi che ogni numero può essere messo in corrispondenza univoca con il proprio quadrato:

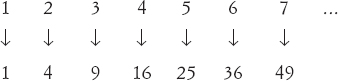
Pertanto i numeri naturali devono essere tanti quanti i quadrati, e dunque la risposta è negativa.

Cantor risolse questa difficoltà riconoscendo che nel dialogo, il termine «più» è usato in due maniere diverse. Salviati nota che l’insieme di tutti i quadrati è un sottoinsieme proprio dell’insieme di tutti i numeri naturali. L’osservazione successiva è più sottile: egli sostiene che esiste una corrispondenza biunivoca tra l’insieme di tutti i quadrati e l’insieme di tutti i numeri naturali. Queste affermazioni sono diverse, ed entrambe possono essere vere senza innescare alcuna contraddizione.

Seguendo questa linea di pensiero, Cantor giunse all’invenzione di un’aritmetica dell’infinito, che spiegava i precedenti paradossi introducendone comunque di nuovi. Quest’opera faceva parte di un programma più esteso definito come Mengenlehre, la matematica degli insiemi (Menge in tedesco significa «insieme» o «unione»). Cantor fu indotto a riflettere sugli insiemi partendo da alcuni problemi complicati nell’analisi di Fourier, e dunque le idee erano radicate nelle teorie matematiche convenzionali. Le risposte cui però egli giunse erano così strane che molti matematici del tempo le rifiutarono completamente. Altri però ne compresero la validità, in particolare David Hilbert, che affermò: «Nessuno ci caccerà dal paradiso che Cantor ha creato».

La dimensione di un insieme

Il punto di partenza di Cantor fu il concetto elementare di insieme, che è una raccolta di oggetti, i suoi membri. Una maniera di specificare un insieme è quella di elencarne i membri, usando le parentesi graffe. Per esempio, l’insieme di tutti i numeri naturali compresi tra 1 e 6 si scrive

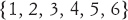
In alternativa, un insieme può essere definito enunciando la regola di appartenenza:

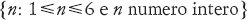
Gli insiemi sopra definiti sono identici. La prima notazione è riservata agli insiemi finiti, mentre la seconda non ha limitazioni di tal sorta. Pertanto, gli insiemi

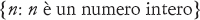
e

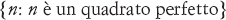
sono entrambi definiti in maniera precisa, e sono entrambi infiniti.

Una delle cose più semplici che possiamo fare con un insieme è contarne i membri. Quanto è grande? L’insieme {1, 2, 3, 4, 5, 6} ha sei membri. Lo stesso vale per l’insieme {1, 4, 9, 16, 25, 36} che è formato dai quadrati corrispondenti. Diciamo che la cardinalità dell’insieme è 6, e definiamo 6 un numero cardinale. (Esiste un concetto differente, quello di numero ordinale, associato con l’ordinamento dei numeri, e per questo motivo in questo caso l’aggettivo «cardinale» non è superfluo). L’insieme di tutti i numeri naturali non può essere contato in questo modo, ma Cantor notò che possiamo comunque stabilire una corrispondenza biunivoca tra l’insieme di tutti i numeri naturali e l’insieme di tutti i quadrati, usando lo stesso schema proposto da Galileo. Ogni numero naturale n è accoppiato con il suo quadrato n².

Cantor definì due insiemi come equinumerosi (non con questo termine) se esiste una corrispondenza biunivoca tra essi. Se gli insiemi sono finiti, questa proprietà è equivalente ad «avere lo stesso numero di membri». Se però gli insiemi sono infiniti, sembra che non abbia senso parlare del numero di membri; nonostante questo il concetto di equinumerosità è assolutamente sensato. Cantor però andò oltre. Introdusse un sistema di numeri transfiniti, o cardinali infiniti, che rese possibile dire quanti membri ha un insieme infinito. Due insiemi, inoltre, erano equinumerosi se e soltanto se avevano lo stesso numero di membri, cioè la stessa cardinalità.

Il punto di partenza era un nuovo tipo di numero, che egli distinse con il simbolo ℵ₀, la prima lettera dell’alfabeto ebraico, l’aleph, con l’aggiunta dell’indice zero, da leggersi aleph-null in tedesco, e ora aleph-zero. Questo numero è per definizione la cardinalità dell’insieme di tutti i numeri interi. Insistendo sul fatto che gli insiemi equinumerosi avessero la stessa cardinalità, Cantor richiese poi che anche ogni insieme che si potesse mettere in corrispondenza biunivoca con l’insieme di tutti i numeri naturali avesse cardinalità ℵ₀. Per esempio, l’insieme di tutti i quadrati ha cardinalità ℵ₀, e lo stesso si può dire per l’insieme di tutti i numeri pari:

La stessa osservazione vale per l’insieme di tutti i numeri dispari:

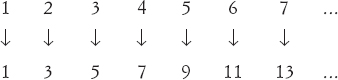
Queste definizioni implicano che un insieme più piccolo può avere la stessa cardinalità di uno più grande. Non esiste però alcuna contraddizione logica qui nelle definizioni di Cantor, e così egli considerò questa caratteristica come una naturale conseguenza del suo apparato, e un prezzo da pagare. Dobbiamo semplicemente stare attenti a non assumere che i cardinali infiniti si comportino esattamente come quelli finiti. Ma perché dovrebbero? Non sono finiti!

I numeri interi (positivi e negativi) sono più dei numeri naturali? Non sono forse il doppio? No, perché possiamo far corrispondere i due insiemi in questa maniera:

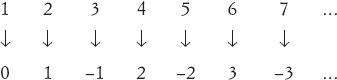
L’aritmetica dei cardinali infiniti è pure stravagante. Per esempio, abbiamo appena visto che gli insiemi dei numeri naturali pari e dispari hanno cardinalità ℵ₀. Poiché questi insiemi non hanno membri in comune, la cardinalità della loro unione (l’insieme formato dalla loro combinazione) dovrebbe, per analogia con gli insiemi finiti, essere ℵ₀ + ℵ₀. Sappiamo però che cosa è l’unione: è rappresentata dai numeri naturali, che hanno cardinalità ℵ₀. A quanto pare siamo allora costretti a dedurre che

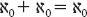
Ed è tutto. Di nuovo però, non esiste contraddizione: non possiamo dividere per ℵ₀, per dedurre che 1 + 1 = 1, perché ℵ₀ non è un numero naturale e la divisione non è stata definita (non abbiamo neppure dimostrato che sia sensata). Questa equazione mostra allora che la divisione per ℵ₀ non ha sempre senso. Di nuovo, accettiamo questo come prezzo per il progresso.

Tutto questo va bene, ma sembra che ℵ₀ sia soltanto un grazioso simbolo per il buon vecchio ∞, e non si dica nulla di nuovo. Non è forse vero che tutti gli insiemi infiniti hanno cardinalità ℵ₀? Siamo sicuri che tutti gli infiniti siano uguali?

Un candidato per una cardinalità infinita maggiore di ℵ₀, cioè un insieme infinito che non possa essere messo in corrispondenza biunivoca con l’insieme di tutti i numeri naturali, è l’insieme di tutti i numeri razionali, indicato in genere con Dopo tutto, ci sono infiniti numeri razionali nell’intervallo compreso tra due interi consecutivi, e il trucchetto che abbiamo usato per gli interi non funziona più.

Ad ogni modo, nel 1873 Cantor dimostrò che anche ha cardinalità ℵ₀. La corrispondenza biunivoca mescola i numeri accuratamente, ma nessuno aveva detto che dovevano rimanere in ordine numerico. Sembrava proprio che ogni insieme infinito avesse cardinalità ℵ₀.

Nello stesso anno, però, Cantor fece un passo avanti. Dimostrò che l’insieme di tutti i numeri reali non ha cardinalità ℵ₀, in uno stupefacente teorema che pubblicò nel 1874. Anche nel senso speciale di Cantor, allora, esistono più reali che interi. Un infinito può essere più grande di un altro infinito.

Quanto è grande la cardinalità dei reali? Cantor sperava che sarebbe stata ℵ₁, il cardinale più grande dopo ℵ₀, ma non fu in grado di dimostrarlo, e così chiamò il nuovo cardinale c, per continuo. L’agognata equazione c = ℵ₁ fu battezzata ipotesi del continuo. Soltanto nel 1960 i matematici evinsero la relazione tra c e ℵ₀, quando Paul Cohen dimostrò che la risposta dipende da quali assiomi scegliamo per la teoria degli insiemi. Con alcuni assiomi ragionevoli, i due cardinali sono uguali, mentre con altri assiomi, parimenti ragionevoli, sono diversi.

Anche se la validità dell’equazione c = ℵ₁ dipende dagli assiomi scelti, lo stesso non vale per un’eguaglianza associata, cioè c = 2^ℵ°. Per ogni cardinale A possiamo definire 2^A come la cardinalità dell’insieme di tutti i sottoinsiemi di A, e possiamo dimostrare, in maniera molto semplice, che 2^A è sempre maggiore di A. Questo significa che non soltanto alcuni infiniti sono più grandi di altri, ma anche che non esiste un cardinale infinito massimo.

Contraddizioni

Il compito principale della matematica dei fondamenti, ad ogni modo, non era dimostrare che i concetti matematici esistono. Era dimostrare che la matematica è coerente in termini logici, perché tutti i matematici sapevano – di fatto, perché tutti loro lo sanno oggi – che potrebbe esistere una certa successione di passi logici, tutti perfettamente corretti, che conducono a una conclusione assurda. Forse potremmo dimostrare che 2 + 2 = 5, oppure che 1 = 0, per esempio. O ancora che 6 è primo, o magari che π = 3.

Ora, potrebbe sembrare che un’unica minima contraddizione abbia conseguenze limitate. Nella vita quotidiana, ci muoviamo in genere molto allegramente in un contesto contraddittorio, sostenendo prima, per esempio, che il riscaldamento globale sta distruggendo il pianeta, e dopo che i voli di linea low-cost sono una grande invenzione. In matematica però, le conseguenze non sono limitate, e non possiamo scampare alle contraddizioni logiche semplicemente ignorandole. In matematica, una volta che abbiamo dimostrato qualcosa, possiamo servircene in altre dimostrazioni. Dalla dimostrazione che 0 = 1, derivano conseguenze molto dannose. Per esempio, tutti i numeri sono uguali. Perché se x è un numero qualunque, partiamo da 0 = 1 e moltiplichiamo ambo i membri per x. Allora 0 = x. In maniera analoga, se y è un altro numero qualunque, 0 = y. Ma allora x = y.

Come risultato ancora peggiore, il metodo standard di dimostrazione per assurdo significa che tutto può essere dimostrato una volta che abbiamo dimostrato che 0 = 1. Per dimostrare l’ultimo teorema di Fermat, per esempio, ragioniamo in questo modo:

Supponiamo che l’ultimo teorema di Fermat sia falso.

Allora (come già dimostrato) 0 = 1.

Contraddizione.

Perciò l’ultimo teorema di Fermat è vero.

Oltre a essere insoddisfacente, questo metodo dimostra anche che l’ultimo teorema di Fermat è falso:

Supponiamo che l’ultimo teorema di Fermat sia vero.

Allora (come già dimostrato) 0 = 1.

Contraddizione.

Perciò l’ultimo teorema di Fermat è falso.

Una volta che tutto è vero – oppure falso – non si può dire nulla di sensato. Tutto l’apparato matematico sarebbe uno stupido gioco, senza alcun contenuto.

Hilbert

Lo sviluppo successivo venne da David Hilbert, forse il più eminente matematico dell’epoca. Hilbert aveva l’abitudine di dedicarsi allo stesso argomento matematico per una decina di anni, risolverne i problemi principali, per poi dedicare l’attenzione a un’altra area. Hilbert si convinse che dovesse essere possibile dimostrare che la matematica non poteva mai condurre a una contraddizione logica. Comprese anche che l’intuizione fisica non sarebbe stata utile in un progetto del genere. Se la matematica è contraddittoria, deve essere possibile dimostrare che 0 = 1, e in questo caso esiste un’interpretazione fisica: 0 mucche = 1 mucca, e dunque le mucche possono scomparire in una nuvola di fumo. Questo sembrava improbabile. Ad ogni modo, non esiste garanzia che la matematica dei numeri naturali renda davvero conto della fisica delle mucche, ed è almeno concepibile che una mucca possa improvvisamente scomparire. (Nella meccanica quantistica, questo potrebbe accadere, ma con una probabilità molto bassa). Esiste un limite al numero di mucche in un universo finito, ma non esiste limite alcuno alla dimensione degli interi matematici. L’intuizione fisica poteva dunque essere fuorviante, e doveva essere ignorata.

Hilbert pervenne a questa convinzione nel suo lavoro sulle basi assiomatiche della geometria euclidea. Scoprì alcune lacune logiche nel sistema di assiomi di Euclide, e comprese che queste lacune si erano aperte perché Euclide era stato deviato dalla sua abitudine a rappresentare il problema in termini visivi. Poiché egli sapeva che una retta era un lungo oggetto sottile, una circonferenza era rotonda e un punto era una macchiolina, aveva inconsciamente assunto certe proprietà di questi oggetti, senza enunciarle come assiomi. Dopo molti tentativi, Hilbert espose un elenco di 21 assiomi e ne discusse il ruolo nella geometria euclidea nella sua opera del 1899 Grundlagen der Geometrie.

Hilbert sosteneva che una deduzione logica deve essere valida, indipendentemente dall’interpretazione assegnatale. Qualunque cosa dipenda da una certa particolare interpretazione degli assiomi, ma fallisca in altre interpretazioni, implica un errore logico. È questa concezione dell’assiomatica, piuttosto che la specifica applicazione alla geometria, la più importante influenza di Hilbert sui fondamenti della matematica. In effetti, la stessa concezione influenzò anche il contenuto della matematica, rendendo molto più semplice (e più rispettabile) inventare nuovi concetti elencando assiomi per essi. Gran parte dell’astrazione della matematica dell’inizio del XX secolo è derivata dalla concezione di Hilbert.

Nell’opinione di molti, Hilbert sosteneva l’idea che la matematica è un gioco di simboli senza senso, ma questo esagera la sua posizione. La sua idea era che allo scopo di porre la materia su una base logica solida, dobbiamo pensare a essa come se fosse un gioco di simboli senza senso. Tutto il resto è irrilevante per la struttura logica. Nessuno però che prenda in seria considerazione le scoperte matematiche di Hilbert, e il suo profondo impegno sull’argomento, può a ragione dedurre che egli pensasse di giocare un gioco senza significato.

Dopo i successi in geometria, Hilbert dedicò le sue attenzioni a un progetto molto più ambizioso: fondare l’intero corpus della matematica su una solida base logica. Seguì da vicino il lavoro dei più eminenti logici, e sviluppò un programma esplicito per classificare i fondamenti della matematica una volta per tutte. Oltre a dimostrare che la matematica era priva di contraddizioni, egli credeva anche che in linea di principio ogni problema potesse essere risolto: ogni enunciato matematico poteva essere dimostrato oppure confutato. Alcuni risultati iniziali positivi lo convinsero di essere sulla strada giusta: il successo non doveva essere lontano.

Gödel

Ci fu un logico, però, che si mostrò scettico in merito alla proposta di Hilbert di dimostrare la consistenza della matematica in termini logici. Il suo nome era Kurt Gödel, e le sue perplessità sul programma di Hilbert mutarono per sempre la nostra visione della verità matematica.

Prima di Gödel, si pensava che la matematica fosse semplicemente vera, e che fosse il più alto esempio di verità, perché la verità di un enunciato come 2 + 2 = 4 era qualcosa che abitava nel regno del pensiero puro, indipendente dal nostro mondo fisico. Le verità matematiche non erano cose che si potevano confutare con esperimenti successivi. In questo esse erano superiori alle verità fisiche, come la legge di gravità di Newton dell’inverso del quadrato, che fu invalidata dall’osservazione del moto del perielio di Mercurio, a supporto della nuova teoria gravitazionale propugnata da Einstein.

Dopo Gödel, la verità matematica si rivelò un’illusione. Quello che esisteva erano dimostrazioni matematiche, che potevano avere una logica interna assolutamente perfetta, ma si collocavano in un contesto più ampio (la matematica dei fondamenti), dove non poteva esserci garanzia che tutto il gioco avesse un qualche significato. Gödel non soltanto sosteneva questo: egli lo dimostrò. Di fatto, fece due cose che insieme trascinarono in rovina l’accurato e ottimistico programma di Hilbert.

Gödel dimostrò che se la matematica è coerente in termini logici, allora è impossibile dimostrarlo. Non soltanto egli non poteva trovare una dimostrazione, ma non esisteva alcuna dimostrazione. Così, come risultato notevole, se riusciamo a dimostrare che la matematica è coerente, segue immediatamente che non lo è. Egli dimostrò anche che alcuni enunciati matematici non possono essere né dimostrati né confutati. Anche in questo caso, non soltanto non era in grado di farlo, ma era proprio impossibile. Enunciati di questo tipo sono detti indecidibili.

In principio Gödel dimostrò questi enunciati nell’ambito di una particolare formulazione logica della matematica, quella adottata da Russell e Whitehead nei Principia Mathematica. Tanto per cominciare, Hilbert pensava che potesse esistere una scappatoia: trovare un fondamento migliore. Quando però i logici studiarono il lavoro di Gödel, fu presto evidente che le stesse idee avrebbero funzionato in qualunque formulazione logica della matematica, abbastanza potente da esprimere i concetti elementari dell’aritmetica.

Un’interessante conseguenza delle scoperte di Gödel è che qualunque sistema assiomatico per la matematica deve essere incompleto: non possiamo mai scrivere un elenco finito di assiomi che distingua in maniera univoca tutti i teoremi come veri o falsi. Non c’era scampo: il programma di Hilbert non poteva funzionare. Quando seppe del lavoro di Gödel, a quanto pare, Hilbert si infuriò moltissimo. La sua collera era forse diretta a se stesso, perché l’idea di fondo nel lavoro di Gödel era molto semplice. (L’implementazione tecnica di quell’idea è particolarmente complicata, ma Hilbert era bravo con i tecnicismi). Hilbert probabilmente comprese che avrebbe dovuto prevedere i teoremi di Gödel.

Russell affondò il libro di Frege con un paradosso logico, quello del barbiere del villaggio che rade soltanto gli uomini che non si radono da sé: l’insieme di tutti gli insiemi che non sono membri di se stessi. Gödel demolì il programma di Hilbert con un altro paradosso logico, quello di qualcuno che dice: «Questa affermazione è una bugia». Perché di fatto l’enunciato indecidibile di Gödel – sul quale poggia tutto il resto – è un teorema T che afferma: «Questo teorema non può essere dimostrato».

Se ogni teorema può essere dimostrato, oppure confutato, allora l’enunciato di Gödel T è contraddittorio in entrambi i casi. Supponiamo che T possa essere dimostrato: allora T afferma che T non può essere dimostrato, e questa è una contraddizione. D’altra parte, se T può essere confutato, allora l’enunciato T è falso, e dunque è sbagliato affermare che T non può essere dimostrato. Di conseguenza T può essere dimostrato, e questa è un’altra contraddizione. L’ipotesi che ogni teorema possa essere dimostrato o confutato ci dice quindi che T può essere dimostrato se e soltanto se T non può essere dimostrato.

Dove siamo ora?

I teoremi di Gödel cambiarono il nostro modo di vedere i fondamenti logici della matematica. Essi implicano che i problemi attualmente irrisolti possono non avere affatto una soluzione: né veri né falsi, ma nel limbo dell’indecidibilità. Molti problemi interessanti si sono rivelati di fatto indecidibili. Ad ogni modo, il lavoro di Gödel non ha avuto, in pratica, l’effetto di estendere molto oltre la regione dei fondamenti in cui si svolse. A ragione o a torto, i matematici impegnati sulla congettura di Poincaré, o sull’ipotesi di Riemann, dedicano il loro tempo alla ricerca di una dimostrazione o di una confutazione. Sanno bene che il problema potrebbe essere indecidibile, e potrebbero anche concepire una dimostrazione di indecidibilità se solo sapessero da che parte cominciare. La maggior parte dei problemi indecidibili noti ha però un aspetto autoreferenziale, e in mancanza di questo, una dimostrazione di indecidibilità sembra comunque inarrivabile.

Mentre la matematica costruiva teorie sempre più complicate sulle spalle di quelle precedenti, la superstruttura della matematica cominciava a cadere a pezzi a causa di ipotesi misconosciute che si rivelavano false. Per puntellare l’edificio, era necessario rinsaldare opportunamente i fondamenti.

Gli studi successivi analizzarono la vera natura dei numeri, lavorando a ritroso dai numeri complessi ai reali, ai razionali per arrivare ai numeri naturali. Il processo però non si fermò lì, mentre anche i sistemi numerici furono reinterpretati in termini di ingredienti ancora più semplici, gli insiemi.

La teoria degli insiemi condusse a notevoli progressi, compreso un ragionevole, per quanto poco ortodosso, sistema di numeri infiniti. Rivelò anche alcuni paradossi fondamentali relativi al concetto di insieme. La soluzione di questi paradossi non risultò, come sperava Hilbert, in una rivendicazione completa della matematica assiomatica, e in una dimostrazione della sua consistenza logica. Fu invece la dimostrazione del fatto che la matematica ha limiti intrinseci, e che alcuni problemi non hanno soluzione. Il risultato fu che il nostro modo di pensare la verità e la certezza matematiche mutò profondamente. È meglio essere consapevoli dei nostri limiti piuttosto che vivere nel paradiso degli stolti.