20.
Caos e complessità
Anche le irregolarità hanno un modello
Alla metà del XX secolo, la matematica ha vissuto una rapida fase di sviluppo, stimolata dalle sue diffusissime applicazioni e potenti nuovi metodi. Una storia completa del periodo moderno della matematica sarebbe lunga almeno quanto un resoconto di tutti gli antefatti. Il meglio che possiamo fare è presentare qualche esempio emblematico, per dimostrare che l’originalità e la creatività in matematica sono vive e vegete. Uno di questi argomenti, che ha raggiunto pubblica notorietà negli anni settanta e ottanta, è dato dalla teoria del caos, che è il nome dato dai mezzi di comunicazione alla dinamica non lineare. La teoria si è evoluta in maniera naturale dai modelli tradizionali usando il calcolo infinitesimale. Un altro esempio è dato dai sistemi complessi, che adottano modi di pensare meno ortodossi, e stanno stimolando la nascita di nuovi concetti matematici e scientifici.
Caos
Prima degli anni sessanta, il termine «caos» aveva un unico significato: disordine senza forma. Da allora però, alcune fondamentali scoperte nella scienza e nella matematica hanno attribuito alla parola un nuovo significato, più sottile, che combina gli aspetti del disordine con quelli della forma. I Philosophiae Naturalis Principia Mathematica di Newton avevano ridotto il sistema del mondo a equazioni differenziali, e queste sono deterministiche. Vale a dire che, una volta noto lo stato iniziale del sistema, il suo futuro è determinato in maniera univoca per tutto il tempo. La concezione di Newton è quella di un universo a orologeria, messo in moto dalla mano del creatore e quindi su un unico percorso inevitabile. È una rappresentazione che sembra non lasciare adito al libero arbitrio, e può essere stata una delle prime fonti della convinzione che la scienza sia fredda e disumana. È comunque una concezione che ci è stata molto utile, e ci ha regalato radio, televisione, radar, telefoni cellulari, velivoli commerciali, satelliti per le comunicazioni, fibre artificiali, plastica e computer.
Lo sviluppo del determinismo scientifico è anche andato di pari passo con una vaga ma ben radicata fede nella conservazione della complessità. Si tratta dell’ipotesi che cause semplici debbano produrre effetti semplici, la quale implica che effetti complessi debbano avere cause complesse. Questa convinzione fa sì che osserviamo un oggetto o un sistema complesso e ci domandiamo da dove venga la complessità. Da dove è venuta, per esempio, la complessità della vita, visto che deve aver avuto origine su un pianeta senza vita? Difficilmente pensiamo che la complessità possa presentarsi di propria iniziativa, ma questa è l’indicazione che proviene dalle ultime tecniche matematiche.
Un’unica soluzione?
La determinatezza delle leggi della fisica segue da un semplice fatto matematico: esiste al più una soluzione di un’equazione differenziale con condizioni iniziali assegnate. In The Hitchhiker’s Guide to the Galaxy di Douglas Adams il supercomputer Pensiero Profondo intraprende una ricerca lunga cinque milioni di anni per fornire la risposta alla domanda fondamentale sulla vita, l’universo e tutto quanto, e come tutti sanno risponde «42». Questo episodio è una parodia di una famosa affermazione in cui Laplace riassumeva la concezione matematica del determinismo:
Un’intelligenza che, in un istante dato, conoscesse tutte le forze che animano la natura e la rispettiva posizione degli esseri che la compongono, e che fosse abbastanza vasta da sottoporre questi dati ad analisi, abbraccerebbe in un’unica formula i movimenti dei più grandi corpi dell’universo e dell’atomo più leggero: per una tale intelligenza nulla sarebbe incerto, e l’avvenire come il passato sarebbe presente ai suoi occhi.
Laplace poi riporta di colpo il lettore con i piedi per terra, aggiungendo:
Lo spirito umano offre, con la perfezione che ha saputo dare all’astronomia, un pallido abbozzo di questa intelligenza.
Ironicamente, era nella meccanica celeste, quella parte della fisica più chiaramente deterministica, che il determinismo laplaciano avrebbe subito un brusco arresto. Nel 1886 re Oscar II di Svezia (che governava anche la Norvegia) mise in palio un premio per la soluzione del problema della stabilità del sistema solare. Il nostro piccolo angolo di universo a orologeria avrebbe continuato a ticchettare per sempre, oppure un pianeta avrebbe potuto entrare in collisione con il Sole o sfuggire nello spazio interstellare? A rigore, le leggi fisiche di conservazione dell’energia e della quantità di moto non impediscono l’una o l’altra eventualità; ma potrebbe la dinamica dettagliata del sistema solare fare maggiore luce?
Poincaré era determinato a vincere il premio, e si riscaldò studiando nel dettaglio un problema più semplice, un sistema di tre corpi celesti. Le equazioni per tre corpi non sono molto più complicate di quelle per due, e hanno più o meno la stessa forma. Poincaré trovò però incredibilmente difficile il suo esercizio con i tre corpi, e scoprì qualcosa di sconvolgente. Le soluzioni di quelle equazioni erano completamente diverse rispetto al caso con due corpi. Di fatto, le soluzioni erano così complicate da non poter essere espresse come una formula matematica. Quel che era peggio, poteva capire abbastanza della geometria (più precisamente, la topologia) della soluzione da dimostrare, senza alcuna ombra di dubbio, che i movimenti rappresentati da quelle soluzioni potevano a volte essere altamente disordinati e irregolari. Poincaré scriveva: «Si rimarrebbe sbalorditi dalla complessità di questa figura che non cerco nemmeno di tracciare. Niente è più adatto a darci un’idea della complessità del problema dei tre corpi». Questa complessità è ora vista come un esempio classico del caos.
Il suo lavoro vinse il premio di re Oscar II, anche se non risolveva del tutto il problema posto. Circa sessant’anni dopo, innescò una rivoluzione nella maniera in cui concepiamo l’universo e le sue relazioni con la matematica.
Negli anni 1926-27 l’ingegnere olandese Balthazar Van der Pol costruì un circuito elettronico per simulare un modello matematico del cuore, e scoprì che sotto certe condizioni l’oscillazione risultante non è periodica, come quella di un normale battito, ma irregolare. Il suo lavoro fu completato da una solida base matematica durante la seconda guerra mondiale, per opera di John Littlewood e Mary Cartwright, in uno studio che traeva origine dall’elettronica dei radar. Ci vollero più di quarant’anni prima che fosse chiara l’ampia portata del loro lavoro.
Dinamica non lineare
Nei primi anni sessanta il matematico americano Stephen Smale inaugurò l’era moderna della teoria dei sistemi dinamici cercando di classificare in maniera esauriente i tipi fondamentali di comportamento dei circuiti elettronici. Al principio si aspettava di trovare delle combinazioni di moti periodici, ma presto comprese la possibilità di un comportamento molto più complicato. In particolare sviluppò il moto complesso scoperto da Poincaré nel problema dei tre corpi ristretto, semplificando la geometria per ottenere un sistema noto come «ferro di cavallo di Smale». Dimostrò che il sistema a ferro di cavallo, per quanto deterministico, presenta alcune caratteristiche casuali. Altri esempi di fenomeni di questo tipo furono sviluppati dalla scuola americana di dinamica e da quella russa, con un contributo particolarmente degno di nota da parte di Oleksandr Sharkovskij e Vladimir Arnold, tanto che cominciò a delinearsi una teoria generale. Il termine «caos» fu introdotto nel 1975 da James Yorke e Tien-Yien Li, in un breve articolo che semplificava uno dei risultati della scuola russa: il teorema di Sharkovskii del 1964, che descriveva un curioso andamento nelle soluzioni periodiche di un sistema dinamico discreto (in cui il tempo scorre per passi discreti invece che in maniera continua).
Nel frattempo, i sistemi caotici facevano la loro comparsa nella letteratura applicata, e di nuovo erano largamente sottovalutati dalla vasta comunità scientifica. Il più famoso di questi fu introdotto dal meteorologo Edward Lorenz nel 1963. Lorenz si era proposto di modellare la convezione atmosferica, approssimando le complicatissime equazioni che regolano questo fenomeno con equazioni molto più semplici in tre variabili. Risolvendole numericamente al computer, scoprì che la soluzione oscillava in una maniera irregolare, quasi casuale. Scoprì anche che risolvendo le stesse equazioni con valori iniziali delle variabili poco diversi, allora le differenze erano amplificate fino a che la nuova soluzione era completamente diversa da quella originaria. La sua descrizione di questo fenomeno nell’ambito di alcune conferenze condusse poi alla definizione, ora popolare, di «effetto farfalla», per indicare come il battito d’ali di una farfalla possa generare, dopo un mese, un uragano dalla parte opposta del globo.
Questo strano scenario è originale, ma in un senso piuttosto particolare. Supponiamo di poter osservare l’evoluzione a livello mondiale del tempo atmosferico due volte: una volta con la farfalla e una volta senza. Saremmo allora sicuri di trovare certamente notevoli differenze, che comprendono magari una volta un uragano e l’altra volta nessun uragano. Simulando al computer le equazioni normalmente usate per prevedere il tempo si ottiene proprio questo effetto, il quale rende molto problematiche le previsioni. Sarebbe però un errore concludere che la farfalla ha causato l’uragano. Nel mondo reale, il tempo non è condizionato da una sola farfalla ma dalle proprietà statistiche di trilioni di farfalle e di altre minuscole interferenze. Nell’insieme, queste alla fine influenzano il luogo e l’istante in cui gli uragani si formeranno, e la direzione che prenderanno in seguito.
L’abbaglio di Poincaré
June Barrow-Green, esaminando gli archivi dell’Institut Mittag-Leffler di Stoccolma, ha recentemente scoperto un aneddoto imbarazzante che era stato occultato in precedenza. Il lavoro che aveva permesso a Poincaré di vincere il premio conteneva un grave errore. Lungi dallo scoprire il caos, come si era ipotizzato, Poincaré aveva sostenuto di dimostrare che non si presentasse. Il lavoro sottoposto in origine dimostrava che tutti i movimenti nel problema dei tre corpi hanno un comportamento del tutto regolare.
In seguito, dopo l’assegnazione del premio, Poincaré individuò un errore, e capì subito che invalidava completamente la sua dimostrazione. L’articolo vincitore del premio era però già stato pubblicato come un numero speciale della rivista dell’istituto. La rivista fu ritirata e Poincaré si accollò i costi di una completa ristampa, che includeva la sua scoperta delle connessioni omocliniche e quello che ora noi chiamiamo caos. Tutta l’operazione gli costò molto di più dell’importo vinto come premio per il lavoro sbagliato. Quasi tutte le copie della versione sbagliata furono ritirate e distrutte, ma una, conservata negli archivi dell’istituto, era sfuggita.
Usando metodi mutuati dalla topologia, Smale, Arnold e i loro collaboratori dimostrarono che le bizzarre soluzioni osservate da Poincaré erano l’inevitabile conseguenza di attrattori strani nelle equazioni. Un attrattore strano è una traiettoria complessa verso la quale il sistema inevitabilmente si dirige. Può essere visualizzato come una forma nello spazio degli stati formato dalle variabili che descrivono il sistema. L’attrattore di Lorenz, che descrive le equazioni di Lorenz in questa maniera, assomiglia un po’ alla maschera del Ranger Solitario, ma quelle che sembrano superfici hanno in realtà un numero infinito di livelli.
Mary Lucy Cartwright (1900-1998)
Mary Cartwright si laureò alla Oxford University nel 1923, una delle sole cinque donne a studiare matematica all’università. Dopo un breve periodo come insegnante, conseguì un dottorato a Cambridge, ufficialmente sotto la guida di Godfrey Hardy, ma in realtà con Edward Titchmarsh, perché Hardy era a Princeton. La sua tesi riguardava l’analisi complessa. Nel 1934 fu nominata assistente professore a Cambridge, e nel 1936 divenne direttore di studi al Girton College.
Nel 1938, in collaborazione con John Littlewood, e su incarico del Dipartimento della ricerca scientifica e industriale, intraprese uno studio delle equazioni differenziali collegate alle applicazioni radar. Insieme scoprirono che queste equazioni hanno soluzioni molto complicate, anticipando in qualche modo il fenomeno del caos. Per questo lavoro fu la prima matematica donna a essere eletta Fellow della Royal Society, nel 1947. Nel 1948 fu eletta Mistress di Girton, e dal 1959 al 1968 fu lettrice all’Università di Cambridge. Ricevette numerosi premi e riconoscimenti, e nel 1969 fu nominata Dama Comandante dell’Impero britannico.
La struttura degli attrattori spiega una curiosa caratteristica dei sistemi caotici: è possibile prevederne il comportamento nel breve termine (diversamente, per esempio, da quello che avviene per il lancio di un dado) ma non nel lungo termine. Perché non possiamo mettere in sequenza molte previsioni a breve termine per creare una previsione a lungo termine? Perché l’accuratezza con la quale possiamo descrivere un sistema caotico si deteriora nel tempo, con velocità sempre crescente, in maniera tale che esiste un orizzonte della previsione oltre il quale non possiamo penetrare. Nondimeno, il sistema rimane sullo stesso attrattore strano, ma la sua traiettoria sull’attrattore cambia in maniera significativa.
Questo risultato cambia il nostro modo di vedere l’effetto farfalla. Tutto quello che le farfalle possono fare è spingere il tempo in posizioni diverse ma sempre sullo stesso attrattore strano, in modo che esso appaia sempre come un tempo perfettamente plausibile. È soltanto poco diverso da quello che sarebbe stato senza tutte quelle farfalle.
David Ruelle e Floris Takens trovarono presto una potenziale applicazione degli attrattori strani in fisica: lo sconcertante problema del flusso turbolento in un fluido. Le equazioni tradizionali per il flusso di fluido, chiamate equazioni di Navier-Stokes, sono equazioni differenziali parziali, e come tali sono deterministiche. Un tipo comune di flusso, il flusso laminare, è regolare e costante, proprio quello che ci aspetteremmo da una teoria deterministica. Un altro tipo di flusso però, quello turbolento, è vorticoso e irregolare, quasi casuale. Teorie precedenti sostenevano che la turbolenza fosse una combinazione estremamente complicata di modelli, peraltro semplici e regolari se considerati a livello singolo, o che le equazioni di Navier-Stokes cessassero di valere nel regime turbolento. Ruelle e Takens proposero però una terza teoria, e ipotizzarono che la turbolenza fosse la manifestazione fisica di un attrattore strano.
In principio questa teoria fu accolta con un certo scetticismo, ma ora sappiamo che era corretta nello spirito, anche se alcuni dei dettagli erano piuttosto discutibili. Seguirono altre fortunate applicazioni, e il termine caos fu accettato come nome adeguato per tutti i comportamenti di questo tipo.
Mostri teorici
Nella nostra storia entra ora un secondo protagonista. Tra il 1870 e il 1930 un altro gruppo di matematici dissidenti inventò una serie di forme bizzarre, con l’unico scopo di mostrare i limiti dell’analisi classica. Nelle prime fasi del calcolo infinitesimale, i matematici avevano ipotizzato che qualunque quantità che variasse in maniera continua dovesse possedere quasi ovunque una velocità di variazione ben definita. Per esempio, un oggetto che si muove nello spazio in maniera continua ha una velocità ben definita, tranne che in un numero relativamente limitato di istanti, in cui la sua velocità cambia bruscamente. Nel 1872, però, Weierstrass mostrò che questa ipotesi da tempo accettata era sbagliata. Un oggetto può muoversi in maniera continua, ma con un comportamento talmente irregolare che, in effetti, la sua velocità cambia bruscamente in ogni istante. Questo significa che in realtà esso non ha affatto una velocità rilevabile.
Tra i membri di questo strano zoo di anomalie vi sono anche una curva che riempie un’intera regione di spazio (una era stata trovata da Peano nel 1890, un’altra da Hilbert nel 1891), una curva che interseca se stessa in ogni punto (scoperta da Waclaw Sierpinski nel 1915) e una curva di lunghezza infinita che racchiude un’area finita. Quest’ultimo esempio di bizzarria geometrica, inventato da Helge von Koch nel 1906, è la curva a fiocco di neve, e si genera come segue. Si parte da un triangolo equilatero, e si aggiungono promontori triangolari al centro di ogni lato per creare una stella a sei punte. Si aggiungono poi promontori più piccoli al centro dei dodici lati della stella, e si procede all’infinito. Vista la sua simmetria di ordine sei, il risultato assomiglia a un complicato fiocco di neve (fig. 20.2). La crescita dei fiocchi di neve reali segue altre regole, ma questa è un’altra storia.
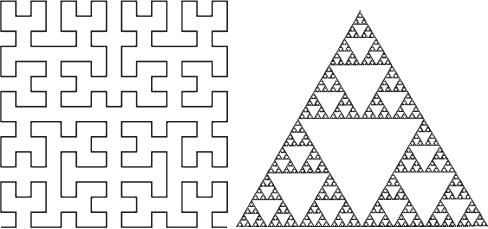
Figura 20.1
Fasi nella costruzione della curva di Hilbert che riempie lo spazio e il triangolo di Sierpinski.
Figura 20.2
La curva a fiocco di neve.
La matematica ortodossa prontamente etichettò queste stranezze come «patologiche» e le collocò in una «galleria di mostri». Con il passare degli anni, però, alcuni imbarazzanti insuccessi richiesero una maggiore attenzione, e le idee dei dissidenti guadagnarono posizioni. La logica sottesa dall’analisi è così raffinata che saltare a conclusioni plausibili può essere pericoloso: i mostri ci avvertono circa quello che può andare storto. Così, al volgere del secolo, i matematici presero confidenza con i pezzi originali esposti dai dissidenti nel loro negozio di curiosità: svilupparono la teoria senza avere alcun serio impatto sulle applicazioni. Di fatto nel 1900 Hilbert poteva definire l’area di ricerca come un paradiso senza scatenare un finimondo.
Negli anni sessanta, contrariamente a tutte le aspettative, la galleria di mostri teorici ebbe un inaspettato impulso in direzione delle scienze applicate. Benoit Mandelbrot comprese che queste curve mostruose aprivano la strada a una teoria delle irregolarità nella natura, che poteva avere conseguenze di vasta portata. Le ribattezzò frattali. Fino ad allora, la scienza era stata soddisfatta di rimanere ancorata a forme geometriche tradizionali come rettangoli e sfere, ma Mandelbrot sosteneva che questa impostazione fosse troppo limitativa. Il mondo naturale è costellato di strutture complesse e irregolari – linee costiere, montagne, nubi, alberi, ghiacciai, sistemi fluviali, onde marine, crateri, cavolfiori – a proposito delle quali la geometria tradizionale non ha nulla da dire. Era necessaria una nuova geometria della natura.
Oggi, gli scienziati hanno inglobato i frattali nel loro schema mentale, proprio come alla fine del XIX secolo i loro predecessori fecero con quelle stravaganti mostruosità matematiche. La seconda parte dell’articolo scritto da Lewis Fry Richardson nel 1926, Atmospherics Diffusion Shown on a Distance-Neighbour Graph, è intitolata «Ha una velocità il vento?» Questa ora è considerata una domanda assolutamente ragionevole. Il flusso atmosferico è turbolento, la turbolenza è frattale e i frattali possono comportarsi come la funzione mostruosa di Weierstrass: possono muoversi in maniera continua senza avere una velocità ben definita. Mandelbrot trovò esempi di frattali in molti settori sia interni che esterni all’ambito scientifico: la forma di un albero, il percorso ramificato di un fiume, le fluttuazioni del mercato azionario.
Caos dappertutto!
Gli attrattori strani dei matematici, visti in termini geometrici, si rivelarono frattali, e i due filoni di pensiero confluirono in quella che è ora universalmente nota come teoria del caos.
Il caos si può presentare di fatto in qualunque area della scienza. Jack Wisdom e Jacques Laskar hanno trovato che la dinamica del sistema solare è caotica. Conosciamo tutte le equazioni, le masse e le velocità necessarie per prevedere il moto futuro per sempre, ma a causa del caos dinamico esiste un orizzonte delle previsioni di circa dieci milioni di anni. Se quindi vogliamo sapere da che lato del Sole si troverà Plutone nell’anno 10 000 000, scordiamocelo! Questi astronomi hanno anche dimostrato che le maree lunari stabilizzano la Terra rispetto agli influssi che condurrebbero altrimenti a un moto caotico, causando una rapida variazione del clima da periodi caldi a età del ghiaccio e ritorno; la teoria del caos dimostra così che senza la Luna, la Terra sarebbe un posto abbastanza inospitale in cui vivere.
Il caos emerge in quasi tutti i modelli matematici delle popolazioni biologiche, ed esperimenti recenti (come permettere agli scarafaggi di riprodursi in condizioni controllate) indicano che si presenta anche in popolazioni biologiche reali. Gli ecosistemi non si assestano normalmente in un qualche tipo di equilibrio naturale statico: al contrario vagano attorno agli attrattori strani, con un andamento abbastanza simile, ma sempre mutante. L’incapacità di comprendere le sottili dinamiche degli ecosistemi è una delle ragioni per cui le risorse ittiche mondiali sono sull’orlo del collasso.
Complessità
Dal caos, passiamo alla complessità. Molti dei problemi che la scienza si trova oggi ad affrontare sono estremamente complicati. Per gestire una barriera corallina, una foresta o una zona di pesca è necessario comprendere un ecosistema altamente complesso, in cui variazioni in apparenza innocue possono innescare problemi inattesi. Il mondo reale è così complicato, e può essere così difficile da misurare, che i metodi tradizionali di modellazione sono difficili da mettere in atto, e persino più difficili da verificare. In risposta a queste sfide, un numero crescente di scienziati è giunto a credere che sia necessario cambiare nettamente il modo in cui modelliamo il nostro mondo.
Nei primi anni ottanta George Cowan, già responsabile di ricerca a Los Alamos, decise che le nuovissime teorie della dinamica non lineare offrissero una via d’uscita. Qui piccole cause possono determinare effetti di vasta portata, regole rigide possono condurre all’anarchia e l’intero spesso ha capacità che non esistono, neppure in forma rudimentale, nei suoi componenti. In termini generali, queste sono esattamente le caratteristiche osservate nel mondo reale. La similitudine si spinge però ancora oltre, abbastanza a fondo da permettere una comprensione totale
Cowan concepì l’idea di un nuovo istituto di ricerca dedicato alle applicazioni interdisciplinari e allo sviluppo della dinamica non lineare. A Cowan si unì Murray Gell-Mann, vincitore di un premio Nobel per la fisica delle particelle, e nel 1984 insieme diedero vita a quello che fu allora chiamato il Rio Grande Institute. Oggi si chiama Santa Fe Institute, un centro internazionale per lo studio dei sistemi complessi. La teoria della complessità ha portato concetti e metodi matematici completamente nuovi, sfruttando i computer per creare modelli digitali della natura. Sfrutta la potenza del computer per analizzare questi modelli e dedurre allettanti caratteristiche dei sistemi complessi. E usa la dinamica non lineare e altre aree della matematica per comprendere quello che i computer rivelano.
Automi cellulari
In un nuovo tipo di modello matematico, conosciuto come automa cellulare, entità come alberi, uccelli e scoiattoli sono rappresentate da piccoli quadratini colorati. Questi competono con i loro vicini in un gioco elettronico matematico. La semplicità è ingannevole: questi giochi si collocano al confine della scienza moderna.
Gli automi cellulari assunsero importanza negli anni cinquanta, quando John von Neumann tentava di comprendere come la vita potesse autoreplicarsi. Stanislaw Ulam ipotizzò di usare un sistema introdotto negli anni quaranta da Konrad Zuse, un pioniere dell’informatica. Immaginiamo un universo popolato da un vasto reticolo di caselle, chiamate cellule, come una gigantesca scacchiera. In ogni istante, una determinata casella può esistere in un certo stato. Questo universo a scacchiera è dotato delle sue proprie leggi di natura, che descrivono come ogni stato cellulare deve variare al passare del tempo nell’istante successivo. È utile rappresentare quello stato con i colori. Allora le regole sarebbero enunciati come: «Se una cellula è rossa e ha due cellule blu adiacenti, deve diventare gialla». Un sistema di questo tipo si chiama automa cellulare (cellulare perché si tratta di un reticolo, automa perché obbedisce ciecamente alle regole qualunque siano).
Per modellare la caratteristica più fondamentale delle creature viventi, Neumann creò una configurazione di cellule che potevano replicarsi, cioè costruire copie di se stesse. Era costituita da 200 000 cellule e impiegava 29 diversi colori per effettuare una descrizione in codice di se stessa. Questa descrizione poteva essere copiata ciecamente, e usata come progetto per costruire ulteriori configurazioni dello stesso tipo. Neumann non pubblicò il suo lavoro fino al 1966; a quel tempo Crick e Watson avevano già scoperto la struttura del DNA e il modo in cui la vita metteva in atto il suo stratagemma di replicazione era ormai chiaro. Gli automi cellulari furono ignorati per altri trent’anni.
Negli anni ottanta si manifestò però un interesse crescente per i sistemi composti da grandi numeri di parti semplici, che interagiscono per produrre un tutto complicato. Per tradizione, la maniera migliore per modellare un sistema in termini matematici è includere il maggior numero possibile di dettagli: più il modello si avvicina alla cosa reale, meglio è. Per sistemi molto complessi, però, questo modo di impostare il problema nei minimi dettagli fallisce. Supponiamo, per esempio, di voler comprendere la crescita di una popolazione di conigli. Non è necessario modellare la lunghezza del pelo dei conigli, la dimensione delle loro orecchie o le modalità di funzionamento del loro sistema immunitario. Bastano poche semplici informazioni per ogni coniglio: l’età, il sesso, il fatto che sia o meno un esemplare gravido. A questo punto possiamo concentrare le risorse del computer su quello che importa davvero.
Quello che la dinamica non lineare fece per loro
Fino a che la dinamica non lineare non divenne un argomento principale nella modellazione scientifica, il suo ruolo rimase per lo più teorico. Il lavoro più approfondito fu quello di Poincaré sul problema dei tre corpi nella meccanica celeste. Questo predisse l’esistenza di orbite altamente complesse, ma fornì soltanto una minima idea del loro aspetto. Il punto centrale del lavoro era dimostrare che equazioni semplici potevano non avere soluzioni semplici, cioè che la complessità non si conserva, ma può avere origini più semplici.
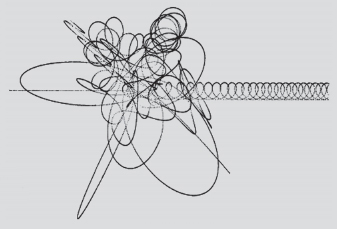
I moderni computer possono calcolare orbite complicate nel problema dei tre corpi.
Per questo tipo di sistema, gli automi cellulari sono molto utili. Rendono possibile ignorare i dettagli superflui sui singoli individui, per concentrarsi invece sul modo in cui gli individui interagiscono. Questa si rivela una maniera eccellente per evincere quali sono i fattori importanti, e per derivare un indizio generale circa il motivo per cui i sistemi complessi fanno quello che fanno.
Geologia e biologia
Un sistema complesso che sfida l’analisi basata su tecniche tradizionali di modellazione è la formazione dei bacini e dei delta fluviali. Peter Burrough ha usato gli automi cellulari per spiegare perché queste caratteristiche naturali adottano la loro forma. L’automa modella l’interazione tra acqua, terreno e sedimento. I risultati spiegano come le differenti velocità di erosione del suolo modificano le forme dei fiumi, e come i fiumi trasportano i detriti, tutti aspetti importanti per l’ingegneria e la gestione fluviale. Gli stessi concetti sono anche interessanti per le compagnie petrolifere, perché greggio e gas si trovano spesso negli strati geologici posti in origine come sedimento.
Un’altra meravigliosa applicazione degli automi cellulari si ha in biologia. Hans Meinhardt ha usato gli automi cellulari per modellare la formazione di motivi negli animali, dalle conchiglie alle zebre. Il fattore chiave è rappresentato dalla concentrazione delle sostanze chimiche. Le interazioni possibili sono le reazioni all’interno di una cellula e i fenomeni di diffusione tra cellule adiacenti. I due tipi di interazione si combinano per generare le regole effettive per lo stato successivo. I risultati sono utili per comprendere i meccanismi di attivazione e di inibizione che attivano e disattivano i geni responsabili del pigmento in maniera dinamica durante la crescita dell’animale.
Stuart Kauffman ha applicato una varietà di tecniche basate sulla teoria della complessità allo studio di un altro grande mistero in biologia: lo sviluppo di una forma organica. La crescita e lo sviluppo di un organismo devono implicare molti aspetti dinamici: non possono essere una semplice traduzione in forma organica delle informazioni contenute nel DNA. Una promettente linea di ricerca consiste nel formulare lo sviluppo come la dinamica di un sistema complesso non lineare.
Gli automi cellulari hanno ora completato il quadro e ci hanno fornito una nuova prospettiva sulle origini della vita. L’automa autoreplicante di Neumann è molto particolare, attentamente progettato per effettuare copie di una configurazione iniziale altamente complessa. Questo è tipico di un automa autoreplicante oppure possiamo ottenere la replicazione senza partire da una configurazione molto particolare? Nel 1993 Hui-Hsien Chou e James Reggia hanno sviluppato un automa cellulare con 29 stati, nel quale uno stato iniziale scelto a caso, o brodo primordiale, conduce a strutture autoreplicanti per più del 98 per cento del tempo. In questo automa, le entità autoreplicanti sono una autentica certezza.
I sistemi complessi supportano l’idea che su un pianeta privo di vita con una chimica sufficientemente complessa, la vita potrebbe nascere spontaneamente e organizzarsi in forme sempre più complicate e sofisticate. Rimane da capire quali tipi di regole conducano all’emergenza spontanea di configurazioni autoreplicanti nel nostro universo, cioè, in breve, quale tipo di leggi fisiche rendano questo primo passo fondamentale verso la vita non soltanto possibile, ma inevitabile.
Quello che la dinamica non lineare fa per noi
Potrebbe sembrare che il caos non abbia alcuna applicazione pratica, essendo irregolare, imprevedibile e molto sensibile a piccoli disturbi. Invece, dato che il caos si basa su leggi deterministiche, si rivela utile proprio sulla base di queste caratteristiche.
Una delle applicazioni potenzialmente più importanti è il controllo caotico. Intorno al 1950 il matematico John von Neumann ipotizzò che l’instabilità del tempo atmosferico potesse un giorno diventare un vantaggio, perché implica che un grande effetto desiderato possa essere generato da un disturbo molto piccolo. Nel 1979 Edward Belbruno comprese che questo effetto poteva essere usato in astronautica per muovere le navicelle spaziali su lunghe distanze con un basso consumo di carburante. Le orbite risultanti richiedono però un lungo tempo – due anni dalla Terra alla Luna, per esempio – e la NASA perse interesse per l’idea.
Nel 1990 il Giappone lanciò una piccola sonda lunare, Hagoromo, che si separava dalla sonda più grande Hiten la quale rimaneva nell’orbita terrestre. Il trasmettitore su Hagoromo subì però un guasto, e lo scopo della sonda Hiten venne meno. Il Giappone voleva salvare qualcosa della missione, ma Hiten disponeva soltanto del 10% del carburante necessario per portare la sonda sulla Luna con un’orbita convenzionale. Un ingegnere del progetto si ricordò dell’idea di Belbruno, e gli chiese di disegnare una nuova rotta. Nell’arco di dieci mesi Hiten era sulla sua traiettoria verso la Luna e oltre, alla ricerca di particelle intrappolate di polvere stellare, e disponeva ancora di metà del carburante restante. La tecnica è stata usata più volte dopo questo primo successo, in particolare per la sonda Genesis inviata nel tentativo di raccogliere un campione di vento solare, e nella missione SmartOne dell’ESA (European Space Agency).
La tecnica si applica sulla Terra come nello spazio. Nel 1990 Celso Grebogi, Edwart Ott e James Yorke hanno pubblicato uno schema teorico generale per sfruttare l’effetto farfalla nel controllo dei sistemi caotici. Il metodo è stato usato per sincronizzare un sistema di laser; per controllare le irregolarità del battito cardiaco, aprendo la strada a un pacemaker intelligente; per controllare le onde elettriche nel cervello, con la possibilità di eliminare gli attacchi epilettici; e per regolarizzare il moto di un fluido turbolento, in modo da potere in futuro rendere gli aerei più efficienti in termini di consumo di carburante.
Come fu creata la matematica
La storia della matematica è lunga e frastagliata. Oltre a compiere notevoli progressi, i pionieri della matematica percorsero vicoli ciechi, a volte per secoli. Questo è però il modo di lavorare dei pionieri. Se è ovvio il cammino da seguire, chiunque può farlo. E così, per circa quattro millenni, quella struttura elaborata ed elegante che chiamiamo matematica è venuta alla luce. Ha proceduto a balzi, con frenetici scoppi di attività seguiti da periodi di stagnazione; il centro di attività si è spostato attorno al globo seguendo l’ascesa e il declino della civiltà umana. Qualche volta è cresciuta secondo le necessità pratiche di quella civiltà, qualche volta le ricerche hanno seguito una direzione propria, quando i partecipanti giocavano quello che a chiunque altro sembrava un puro gioco intellettuale. E spesso a sorpresa, quel gioco alla fine aveva un riscontro nel mondo reale, stimolando lo sviluppo di nuove tecniche, nuovi concetti e nuovi punti di vista.
La matematica non si è fermata. Nuove applicazioni richiedono una nuova matematica, e i matematici rispondono all’appello. La biologia, in particolare modo, pone nuove sfide alla modellazione e alla comprensione matematica. I requisiti interni della matematica continuano a stimolare nuove idee e nuove teorie. Molte importanti congetture sono ancora irrisolte, ma i matematici ci stanno lavorando.
Nonostante la sua lunghissima storia, la matematica ha preso la sua ispirazione da queste due fonti: il mondo reale e il mondo dell’immaginazione umana. Qual è il più importante? Né l’uno né l’altro. Quello che importa è la combinazione dei due. La storia insegna che la matematica trae la sua potenza, e la sua bellezza, da entrambi. L’epoca degli antichi greci è spesso vista come un’Età dell’oro storica, nella quale la logica, la matematica e la filosofia furono portate a rapportarsi alla condizione umana. I progressi ottenuti dai greci sono però soltanto parte di una storia in corso. La matematica non è mai stata così attiva, non è mai stata così varia, e non è mai stata così vitale per la nostra società.
Diamo il benvenuto all’Età dell’oro della matematica.
