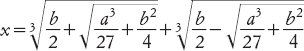10.

Quantità impossibili

I numeri negativi possono avere una radice quadrata?

I matematici distinguono molti tipi di numeri differenti, con proprietà diverse. Quello che importa realmente non sono i singoli numeri, ma il sistema a cui appartengono, la compagnia che hanno.

Quattro di questi sistemi di numeri sono familiari: i numeri naturali, 1, 2, 3…; gli interi, che comprendono anche lo zero e i numeri interi negativi; i numeri razionali, composti di frazioni p/q dove p e q sono interi e q è diverso da zero; e i numeri reali, introdotti in genere come decimali che possono susseguirsi all’infinito, qualunque cosa questo significhi, e rappresentano sia i numeri razionali, come decimali che si ripetono, sia i numeri irrazionali come 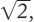e e π, le cui espansioni decimali non ripetono sempre lo stesso gruppo di cifre.

Interi

Il nome «intero» significa semplicemente «completo»; gli altri nomi danno l’impressione che i sistemi in questione siano cose sensate e ragionevoli: naturali, razionali e ovviamente reali. Questi nomi riflettono, e suggeriscono, il concetto a lungo predominante che i numeri siano espressione del mondo intorno a noi.

Molti pensano che l’unico modo per fare ricerca matematica sia inventare nuovi numeri. Questa visione è quasi sempre sbagliata; buona parte della matematica non riguarda affatto i numeri, e in ogni caso l’obiettivo è sempre quello di inventare nuovi teoremi, non nuovi numeri. Talvolta, comunque, si presentano «nuovi numeri». E un’invenzione del genere, un numero cosiddetto «impossibile» o «immaginario» ha cambiato il volto della matematica, aggiungendo ad essa un’incredibile potenza. Quel numero era la radice quadrata di meno uno. Per i matematici dei tempi passati, una descrizione del genere sembrava ridicola, perché il quadrato di qualunque numero è sempre positivo. I numeri negativi non possono dunque avere una radice quadrata. Supponiamo però che l’abbiano. Che cosa accadrebbe?

Ci volle molto tempo prima che i matematici realizzassero che i numeri sono artefatti inventati dagli uomini; artefatti molto efficaci per catturare diversi aspetti della natura, di certo, che però non sono parte della natura più di uno dei triangoli di Euclide o di una formula nel calcolo infinitesimo. Nella storia, vediamo che i matematici si scontrarono per la prima volta con questo problema filosofico quando cominciarono a comprendere che i numeri immaginari erano inevitabili, utili e per certi versi alla pari con i più familiari reali.

Problemi con le cubiche

Le idee matematiche rivoluzionarie raramente sono scoperte nel contesto più semplice e (con il senno di poi) più ovvio. Nella maggior parte dei casi emergono da qualcosa di molto più complicato. Fu così con la radice quadrata di meno uno. Oggi, noi solitamente introduciamo questo numero partendo dall’equazione quadratica x² + 1 = 0, la cui soluzione è la radice quadrata di meno uno, qualunque cosa significhi. Tra i primi matematici a chiedersi se una soluzione del genere avesse un significato sensato ci furono gli algebristi del Rinascimento, che si imbatterono nelle radici quadrate di numeri negativi in una maniera indiretta inaspettata: la soluzione delle equazioni cubiche.

Ricordiamo che del Ferro e Tartaglia scoprirono le soluzioni algebriche delle equazioni cubiche, in seguito esposte da Cardano nella sua Ars magna. Nella simbologia moderna, la soluzione di una equazione cubica x³ + ax = b è

I matematici del Rinascimento avevano espresso questa soluzione a parole, ma il procedimento era lo stesso.

Talvolta questa formula funzionava benissimo, ma talvolta presentava dei problemi. Cardano notò che quando la formula è applicata all’equazione x³ = 15x + 4, con l’ovvia soluzione x = 4, il risultato è espresso come

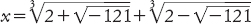
Questa espressione sembra non avere alcun significato sensato, comunque, perché −121 non ha radice quadrata. Cardano, perplesso, scrisse a Tartaglia chiedendo lumi, ma Tartaglia non capì e la sua risposta non fu di aiuto.

Una specie di risposta venne da Rafael Bombelli nella sua opera in tre volumi L’Algebra, stampata a Venezia nel 1572 e a Bologna nel 1579. Bombelli era preoccupato che l’Ars Magna di Cardano fosse piuttosto oscura, e si era proposto di scrivere un’esposizione più chiara. Trattò quell’antipatica radice quadrata come un numero ordinario, notando che

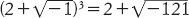
e deducendo la curiosa formula

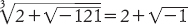
In maniera analoga, Bombelli ottenne la formula

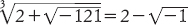
Ora egli poteva riscrivere la somma di due radici cubiche come

Questo strano metodo condusse dunque alla soluzione corretta, un normalissimo intero, ma ci riuscì manipolando quantità «impossibili».

Tutto questo era interessante, ma perché funzionava?

Numeri immaginari

Per rispondere alla domanda, i matematici dovevano concepire una maniera opportuna per pensare alle radici quadrate dei numeri negativi, ed effettuare con esse dei calcoli. I primi a mettere per iscritto le proprie ricerche, e tra questi Descartes e Newton, interpretarono questi numeri immaginari come un indizio del fatto che un problema non abbia soluzione. Se volessimo trovare un numero il cui quadrato fosse meno uno, la soluzione formale, la radice quadrata di meno uno, sarebbe immaginaria, e dunque non si avrebbe alcuna soluzione. Il calcolo di Bombelli però implicava che i numeri immaginari fossero molti di più. Potevano essere usati per trovare soluzioni: si presentavano quando le soluzioni esistevano.

Nel 1673 John Wallis inventò una maniera semplice per rappresentare i numeri immaginari come punti in un piano. Partì dalla consueta rappresentazione dei numeri reali su una retta, con i numeri positivi a destra e i negativi a sinistra.

Introdusse poi un’altra retta, ad angolo retto con la prima, e lungo questa nuova retta sistemò i numeri immaginari.

Si tratta di un approccio simile a quello di Descartes per la geometria piana, con l’uso di assi coordinati. I numeri reali formano un asse nella figura, i numeri immaginari un altro. Wallis non enunciò l’idea proprio in questa forma: la sua versione era più vicina alla concezione delle coordinate di Fermat piuttosto che a quella di Descartes. Gli aspetti fondamentali sono però gli stessi. Il resto del piano corrisponde ai numeri complessi, che hanno due parti: una reale, una immaginaria. Nelle coordinate cartesiane, misuriamo la parte reale lungo la retta reale e misuriamo la parte immaginaria parallelamente alla retta immaginaria. Quindi 3 + 2i si trova 3 unità a destra dell’origine e 2 unità in alto.

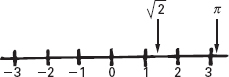
Figura 10.1

La retta dei numeri reali.

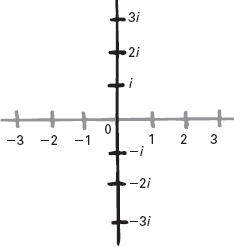
Figura 10.2

Due copie della retta dei numeri reali, disposte ad angolo retto.

L’idea di Wallis risolveva il problema di attribuire un significato ai numeri immaginari, ma nessuno lo notò minimamente. Ad ogni modo, la sua idea lentamente si affermò nel subconscio matematico. La maggior parte dei matematici smise di preoccuparsi che la radice quadrata di meno uno non potesse occupare una posizione sulla retta reale, e comprese che poteva vivere da qualche parte nel più ampio mondo del piano complesso. Alcuni non colsero la portata dell’idea: nel 1758 François Daviet de Foncenex, in un articolo sui numeri immaginari, affermò che non aveva senso pensare che gli immaginari formassero una linea ad angolo retto con la linea dei reali. Altri però presero la questione a cuore e ne compresero l’importanza.

L’idea che un piano complesso possa estendere la confortevole retta reale e dare agli immaginari una casa era implicita nel lavoro di Wallis, ma lievemente oscurata dal modo in cui l’autore l’aveva presentata. Fu esplicitata dal norvegese Caspar Wessel nel 1797. Wessel era un topografo, e il suo interesse principale era rappresentare la geometria del piano in termini di numeri. Lavorando a ritroso, le sue idee potrebbero essere viste come un metodo per rappresentare i numeri complessi in termini della geometria planare. Egli però pubblicò in danese, e il suo lavoro non ottenne riscontro fino a un secolo dopo, quando fu tradotto in francese. Nel 1806 il matematico francese Jean-Robert Argand, in maniera indipendente, pubblicò la stessa rappresentazione dei numeri complessi, e nel 1811 Gauss la scoprì di nuovo in maniera indipendente da entrambi.

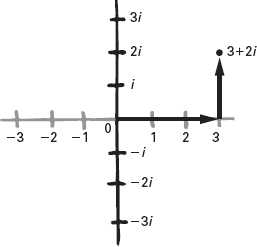
Figura 10.3

Il piano complesso secondo Wessel.

Analisi complessa

Se i numeri complessi fossero stati buoni soltanto per l’algebra, sarebbero rimasti una curiosità intellettuale, di poco interesse al di fuori della matematica pura. Quando però l’interesse nel calcolo infinitesimo crebbe, e assunse una forma più rigorosa come analisi, tutti cominciarono a notare che una fusione davvero interessante dell’analisi reale con i numeri complessi – l’analisi complessa – non soltanto era possibile, ma auspicabile. E inoltre, per molti problemi, essenziale.

Questa scoperta derivò dai primitivi tentativi di pensare a funzioni complesse. Le funzioni più semplici, come il quadrato o il cubo, dipendevano soltanto da manipolazioni algebriche, e dunque era semplice definire queste funzioni per numeri complessi. Per calcolare il quadrato di un numero complesso, dobbiamo semplicemente moltiplicarlo per se stesso, con lo stesso procedimento applicato a un numero reale. Le radici quadrate di numeri complessi sono un po’ più complicate, ma lo sforzo garantisce una piacevole ricompensa: ogni numero complesso ha una radice quadrata. Di fatto, ogni numero complesso diverso da zero ha precisamente due radici quadrate, uguali e con segno opposto. Non soltanto si erano dunque ampliati i numeri reali con un nuovo numero, i, dotando − 1 di una radice quadrata, ma si era fornita una radice quadrata a qualunque numero nel sistema allargato dei numeri complessi.

Che dire a proposito di seni, coseni, funzioni esponenziali e logaritmi? A questo punto, le cose cominciavano a farsi molto interessanti, ma anche molto problematiche, soprattutto nel caso dei logaritmi.

Come anche i, i logaritmi dei numeri complessi comparivano in problemi puramente reali. Nel 1702 Johann Bernoulli stava studiando il processo di integrazione, applicato ai reciproci delle forme quadratiche. Conosceva una tecnica ingegnosa per effettuare questa operazione ogni volta che l’equazione quadratica in oggetto aveva due soluzioni reali, r e s. Possiamo allora riscrivere l’espressione per integrarla in termini di «frazioni parziali»

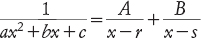
e questa porta all’integrale

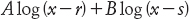
Che cosa accade però se la quadratica non ha radici reali? Come possiamo integrare il reciproco di x² + 1, per esempio? Bernoulli comprese che una volta definita l’algebra complessa, il trucco della frazione parziale funziona ancora, ma ora r e s sono numeri complessi. Così, per esempio,

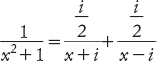
e l’integrale di questa funzione assume la forma

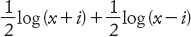
Il passaggio finale non era del tutto soddisfacente, perché richiedeva una definizione del logaritmo di un numero complesso. Era possibile formulare questa quantità in maniera sensata?

Bernoulli pensava di sì, e proseguì a usare la sua nuova idea con risultati eccellenti. Anche Leibniz adottò questa linea di pensiero, ma i dettagli matematici non erano semplici. Nel 1712 entrambi stavano riflettendo su una caratteristica del tutto fondamentale di questa impostazione. Dimentichiamo i numeri complessi: qual era il logaritmo di un numero reale negativo? Bernoulli pensava che il logaritmo di un numero reale negativo dovesse essere reale; Leibniz insisteva che fosse complesso. Bernoulli aveva concepito una specie di dimostrazione per la sua affermazione: assumendo il formalismo consueto del calcolo infinitesimale, l’equazione

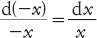
può essere integrata

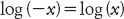
Ad ogni modo, Leibniz non era convinto, e credeva che l’integrazione fosse corretta soltanto per reali positivi x.

Questa particolare controversia fu risolta da Eulero nel 1749, a favore di Leibniz. Bernoulli, affermò Eulero, aveva dimenticato che ogni integrazione implica una costante arbitraria. Quello che Bernoulli doveva aver dedotto era che

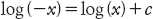
per una certa costante c. Qual era questa costante? Se i logaritmi dei numeri negativi (e complessi) devono comportarsi come i logaritmi dei numeri reali positivi (e questo è il punto di tutta la questione) allora dovrebbe essere vero che

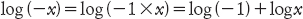
in maniera tale che c = log(−1). Eulero allora si imbarcò in una serie di bellissimi calcoli che produssero una forma più esplicita per c. In primo luogo, trovò un modo per manipolare diverse formule con numeri complessi, assumendo che si comportassero assolutamente come numeri reali, e dedusse una relazione tra le funzioni trigonometriche e l’esponenziale

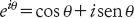
una formula che era stata anticipata nel 1714 da Roger Cotes. Ponendo θ = π Eulero ottenne il meraviglioso risultato

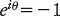
il quale mette in relazione le due costanti matematiche fondamentali e e π. È notevole che una relazione del genere esista, ed è ancora più notevole che sia così semplice. Questa formula è sempre in cima alla classifica per la «più bella formula di tutti i tempi».

Se calcoliamo il logaritmo, deduciamo subito che

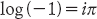
rivelando il segreto di quella misteriosa costante c precedente: è iπ. In quanto tale, è immaginaria, e dunque Leibniz aveva ragione mentre Bernoulli aveva torto.

Ad ogni modo, c’è di più, e si apre il vaso di Pandora. Se poniamo θ = 2π, allora

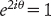
Di conseguenza log(1) = 2iπ. L’equazione x = x × 1 implica che

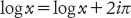
e da questa concludiamo che se n è un numero intero qualsiasi,

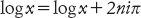
A prima vista, questo non ha senso, perché sembra implicare che 2niπ = 0 per ogni n. Esiste però un modo di interpretare la relazione in modo che abbia un senso. Sui numeri complessi, la funzione logaritmo assume più valori. Di conseguenza, a meno che il numero complesso z non sia zero, la funzione logz può assumere un numero infinito di valori distinti. (Se z = 0, il valore log0 non è definito).

I matematici erano abituati a funzioni che potevano assumere diversi valori distinti, come la radice quadrata che rappresenta l’esempio più banale: in questo caso, anche un numero reale ha due radici quadrate distinte, una positiva e l’altra negativa. Ma un numero infinito di valori? Questo era molto strano.

Il teorema di Cauchy

Quello che creò davvero scompiglio fu scoprire che era possibile applicare il calcolo infinitesimale – l’analisi – alle funzioni complesse, e che la teoria risultante era elegante e utile. Così utile, infatti, che il fondamento logico dell’idea cessava di essere una questione importante. Se qualcosa funziona, e sentiamo di averne bisogno, in genere non continuiamo a chiederci se ha senso.

Sembra che l’introduzione dell’analisi complessa sia stata una decisione cosciente da parte della comunità matematica: una generalizzazione tanto ovvia e irresistibile che ogni matematico con la minima sensibilità per la materia avrebbe voluto vederne l’applicazione. Nel 1811 Gauss scrisse una lettera a un amico, l’astronomo Friedrich Bessel, rivelando la sua rappresentazione dei numeri complessi come punti in un piano; faceva riferimento anche ad alcuni profondi risultati. Tra questi c’è un teorema fondamentale su cui poggia tutta l’analisi complessa. Oggi lo chiamiamo teorema di Cauchy, perché fu pubblicato da Cauchy, ma Gauss aveva espresso l’idea molto tempo prima nei suoi manoscritti inediti.

Questo teorema riguarda gli integrali definiti di funzioni complesse, vale a dire espressioni del tipo

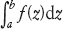
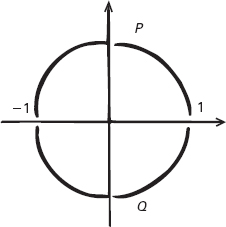
Figura 10.4

Due percorsi distinti P e Q da − 1 a 1 nel piano complesso.

dove a e b sono numeri complessi. Nell’analisi reale questa espressione può essere valutata trovando una funzione F(z) antiderivata di f(z), cioè una funzione F(z) tale che la sua derivata dF(z)/dz = f(z). L’integrale definito è allora uguale a F(b) − F(a). In particolare, il suo valore dipende soltanto dai punti estremi a e b, e non da come ci si sposta da uno all’altro.

L’analisi complessa, diceva Gauss, è diversa. In questo caso il valore dell’integrale può dipendere dal percorso che la variabile z percorre da a a b. Dal momento che i numeri complessi formano un piano, la loro geometria è più ricca di quella della retta reale, ed è qui che conta questa ricchezza aggiuntiva.

Supponiamo per esempio di integrare f(z) = 1/z da a = −1 a b = 1. Se il percorso in questione è una semicirconferenza P posta al di sopra dell’asse reale, allora l’integrale risulta −πi. Se però il percorso è una semicirconferenza Q posta al di sotto dell’asse reale, allora l’integrale risulta πi. I due valori sono diversi, e la differenza è 2πi.

Questa differenza, sosteneva Gauss, si ha perché la funzione 1/z ha uno spiacevole comportamento. Diventa infinita all’interno della regione racchiusa dai due percorsi, di fatto nel punto z = 0, che rappresenta il centro della circonferenza formata dai due percorsi. Gauss scriveva così a Bessel: «Se questo non accade però […] io sostengo che l’integrale ha soltanto un valore anche se calcolato su percorsi differenti a patto che [la funzione] non diventi infinita nello spazio racchiuso dai due percorsi. Questo è un teorema davvero meraviglioso, la cui dimostrazione fornirò in un’occasione opportuna». Gauss però non lo fece mai.

Il teorema fu invece scoperto nuovamente, e pubblicato da Augustin-Louis Cauchy, il vero fondatore dell’analisi complessa. Gauss aveva forse avuto l’idea, ma le idee sono inutili se nessuno ne viene a conoscenza. Cauchy pubblicò il suo lavoro. Di fatto, Cauchy pubblicò quasi a getto continuo. Si dice che la regola, valida ancora oggi, che vieta alla rivista «Comptes Rendus de l’Académie Française» di accettare articoli più lunghi di quattro pagine, sia stata introdotta esplicitamente per impedire a Cauchy di riempirla con la sua vasta produzione. Quando però la regola fu introdotta, Cauchy cominciò a scrivere una gran quantità di articoli brevi. Dalla sua prolifica penna emersero rapidamente le linee principali dell’analisi complessa. E si tratta di una teoria più semplice, più elegante e per molti versi più completa rispetto all’analisi reale, all’interno della quale tutta l’idea aveva avuto inizio.

Nell’analisi reale, per esempio, una funzione può essere differenziabile, ma la sua derivata può non esserlo. Può essere differenziabile 23 volte, ma non 24. Può essere differenziabile un numero di volte a piacere, ma può non avere una rappresentazione in serie di potenze. Nessuna di queste brutte cose può accadere nell’analisi complessa. Se una funzione è differenziabile, allora può essere differenziabile quante volte vogliamo, e inoltre ha una rappresentazione in serie di potenze. La ragione, strettamente collegata al teorema di Cauchy e probabilmente usata da Gauss nella sua dimostrazione sconosciuta, è che per essere differenziabile, una funzione complessa deve soddisfare alcuni vincoli molto stretti, noti come equazioni di Cauchy-Riemann. Queste equazioni conducono direttamente al risultato di Gauss che l’integrale tra due punti può dipendere dal percorso scelto. In maniera equivalente, come Cauchy aveva notato, l’integrale lungo un percorso chiuso non deve necessariamente essere zero. Ha un valore nullo a condizione che la funzione sia differenziabile (così in particolare non è infinita) in tutti i punti all’interno del percorso.

C’era anche un teorema, il teorema del residuo, che diceva il valore di un integrale lungo un percorso chiuso, e dipendeva soltanto dalla posizione dei punti in cui la funzione diventava infinita, e dal suo andamento nelle vicinanze di quei punti. In breve, l’intera struttura di una funzione complessa è determinata dalle sue singolarità, cioè i punti in cui si comporta male. E le singolarità più importanti sono i suoi poli, i punti in cui la funzione diventa infinita.

La radice quadrata di meno uno fece arrovellare i matematici per secoli. Anche se un numero del genere sembrava non esistere, risultava dai calcoli. E c’era il sospetto che il concetto dovesse avere un senso, perché poteva essere usato per ottenere risultati del tutto validi che da parte loro non implicavano il calcolo della radice quadrata di un numero negativo.

Con il crescente successo delle applicazioni di questa quantità impossibile, i matematici cominciarono ad accettarla come uno strumento utile. Il suo stato rimase incerto fino a che non si comprese che esiste un’estensione coerente dal punto di vista logico del sistema tradizionale dei numeri reali, in cui la radice quadrata di meno uno è un nuovo tipo di quantità, un’estensione che comunque obbedisce a tutte le leggi tradizionali della matematica.

In termini geometrici, i numeri reali costituiscono una retta e i numeri complessi costituiscono un piano: la retta reale è uno dei due assi di questo piano. In termini algebrici, i numeri complessi non sono altro che coppie di numeri reali con formule particolari per sommare o moltiplicare le coppie.

Una volta accettati come quantità ragionevoli, i numeri complessi si diffusero rapidamente in tutta la matematica perché semplificavano i calcoli ed evitavano la necessità di considerare separatamente i numeri positivi e quelli negativi. A tal riguardo possono essere considerati in analogia alla precedente invenzione dei numeri negativi, che evitavano la necessità di trattare in maniera diversa l’addizione e la sottrazione. Oggi, i numeri complessi, e il calcolo infinitesimo con funzioni complesse, sono normalmente considerati come una tecnica indispensabile in quasi tutti i campi della scienza, dell’ingegneria e della matematica.