3.
Notazioni e numeri
Da dove vengono i nostri simboli numerici
Siamo così abituati al sistema numerico attuale, con le sue dieci cifre della numerazione decimale 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 (nei paesi occidentali), che può essere traumatico scoprire l’esistenza di maniere completamente diverse di scrivere i numeri. Anche oggi, molte culture (arabi, cinesi, coreani) usano simboli differenti per le dieci cifre, anche se tutti combinano questi simboli per rappresentare numeri più grandi usando lo stesso metodo «posizionale» (centinaia, decine, unità). Le diversità di notazione possono essere però ancora più radicali. Non c’è nulla di speciale nel numero 10. Si dà il caso che sia il numero delle dita delle nostre mani, che sono ideali per contare, ma se fossimo evoluti con sette dita, o dodici, sistemi molto simili avrebbero funzionato altrettanto bene, forse meglio in alcuni casi.
Numerali romani
La maggior parte degli occidentali conosce almeno un sistema alternativo, i numerali romani, in cui, per esempio, l’anno 2012 si scrive MMXII. La maggior parte di noi sa anche bene, almeno se ci viene ricordato, che usiamo due metodi distinti per scrivere i numeri che non sono interi: frazioni come 1/3 e decimali come 0,75. Un’altra notazione numerica, che troviamo nelle calcolatrici, è quella scientifica adottata per numeri molto grandi o molto piccoli, come 5 × 109 per cinque miliardi (spesso scritto come 5E9 sul display della calcolatrice) o 5 × 10−6 per cinque milionesimi.
Questi sistemi simbolici sono stati sviluppati nel corso di migliaia di anni, e nelle diverse culture si sono affermate molte alternative. Abbiamo già incontrato il sistema sessagesimale dei babilonesi (che sarebbe naturale per ogni creatura dotata di 60 dita), e i simboli numerici egiziani, più semplici e più limitati, con quello strano procedimento usato per le frazioni. In un periodo successivo, in America Centrale, la civiltà maya adottò un sistema di numerazione in base 20. Soltanto in tempi recenti l’umanità si è uniformata sui metodi usati oggi per scrivere i numeri, secondo una consuetudine stabilita in termini di tradizione e convenienza. La matematica tratta i concetti, non i simboli, ma una scelta opportuna dei simboli può essere molto utile.
Numerali greci
Iniziamo la storia dei simboli con i greci. La geometria greca rappresentò un notevole progresso rispetto alla geometria dei babilonesi, ma non si può dire lo stesso dell’aritmetica greca (per quanto possiamo saperne dalle fonti giunte fino a noi). I greci avevano fatto un passo indietro: non usavano la notazione posizionale. Esistevano invece simboli appositi per i multipli di 10 e 100, e dunque, per esempio, il simbolo usato per il numero 50 non aveva una particolare relazione con quello usato per il 5 o il 500.
La più antica espressione dei numerali greci
risale al 1100 a. C. circa. Nel 600 a. C. i simboli erano cambiati,
e nel 450 a. C. erano stati sostituiti di nuovo, con l’adozione del
sistema attico, che ricorda i numerali romani. Il sistema attico
usava  per i numeri 1, 2, 3 e 4.
Per il 5 si usava la lettera greca maiuscola pi Π, forse perché è
la prima lettera di penta (cinque). Per lo stesso motivo, 10 si
scriveva Δ, la prima lettera di deka; 100 si scriveva H, la prima
lettera di hekaton; 1000 si scriveva
per i numeri 1, 2, 3 e 4.
Per il 5 si usava la lettera greca maiuscola pi Π, forse perché è
la prima lettera di penta (cinque). Per lo stesso motivo, 10 si
scriveva Δ, la prima lettera di deka; 100 si scriveva H, la prima
lettera di hekaton; 1000 si scriveva 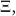 la prima lettera di
chilioi; e 10000 si scriveva M, la prima lettera di myrioi. In
seguito Π venne sostituito da Γ. Con questa notazione, il numero
2178, per esempio, si scriveva come
la prima lettera di
chilioi; e 10000 si scriveva M, la prima lettera di myrioi. In
seguito Π venne sostituito da Γ. Con questa notazione, il numero
2178, per esempio, si scriveva come
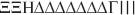
Benché i pitagorici facessero dei numeri la base della loro filosofia, non sappiamo in che modo li scrivessero. Il loro interesse per i numeri quadrati e triangolari suggerisce che potessero rappresentare i numeri con configurazioni di puntini. Nel periodo classico, dal 600 al 300 a. C., il sistema greco aveva subito una nuova modifica, e per indicare i numeri da 1 a 900 erano usate le 27 lettere dell’alfabeto, come mostra la figura 3.1.
Queste sono le lettere greche minuscole con tre
lettere aggiuntive derivate dall’alfabeto fenicio:  (stigma),
(stigma), 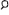 (koppa) e
(koppa) e 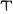 (sampi).
(sampi).
L’uso delle lettere al posto dei numeri poteva causare ambiguità, e così sopra i simboli numerici fu apposta una linea orizzontale. Per i numeri maggiori di 999, il valore di un simbolo poteva essere moltiplicato per 1000 anteponendo ad esso un trattino.
I diversi sistemi greci erano ragionevoli per registrare i risultati dei calcoli, ma non per eseguire le operazioni in sé. (Immaginate di provare a moltiplicare σμγ per ωλδ, per esempio). Le operazioni vere e proprie erano probabilmente effettuate con un abaco, magari rappresentato da sassolini sulla sabbia, soprattutto nei primi tempi.
I greci scrivevano le frazioni in maniere diverse. Si potevano comporre scrivendo il numeratore, seguito da un apostrofo (′), e poi il denominatore, seguito da un doppio apostrofo (″). Spesso il denominatore era scritto due volte. Con questa notazione 21/47 sarebbe stato scritto come
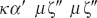
dove κα è 21 e μζ è 47. Usavano anche le frazioni introdotte dagli egizi, e avevano un simbolo speciale per 1/2. Alcuni astronomi greci, in particolare Tolomeo, usavano il sistema sessagesimale babilonese per la sua precisione, ma usavano i simboli greci come cifre di base. Era tutto molto diverso da quello che conosciamo oggi, e in effetti, era tutto molto complicato.

Figura 3.1
Il sistema numerico greco.
Simboli numerici indiani
I dieci simboli tradizionalmente usati per rappresentare le cifre decimali sono spesso definiti come numerali indo-arabi, perché ebbero origine in India e furono adottati e sviluppati dagli arabi.
I primi numeri indiani erano più vicini al sistema egizio. Per esempio, i numerali kharosthi, in uso dal 400 a. C. fino al 100 d. C., rappresentano i numeri da 1 a 8 come
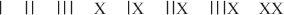
con un simbolo speciale per il 10. Le prime tracce di quello che alla fine divenne il sistema simbolico moderno apparvero nel 300 a. C. circa, nei numeri di brahmi. Su alcune iscrizioni buddhiste del tempo compaiono i precursori dei successivi simboli hindu per 1, 4 e 6. Ad ogni modo, il sistema brahmi usava simboli differenti per multipli di dieci o di cento, ed era dunque simile al simbolismo numerico greco, tranne per il fatto che usava simboli speciali piuttosto che lettere dell’alfabeto. Il sistema brahmi non era di tipo posizionale. Nel 100 d. C. troviamo testimonianza del sistema brahmi completo. Alcune iscrizioni rinvenute in caverne o su monete mostrano che rimase in uso fino al IV secolo.
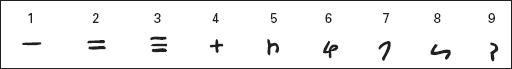
Figura 3.2
Numerali brahmi da 1 a 9.
Tra il IV e il VI secolo, l’impero Gupta ottenne il controllo di una vasta regione dell’India, e i numerali brahmi si trasformarono nei numerali gupta. In seguito mutarono ancora nei numerali nagari. L’idea era la stessa, ma i simboli usati erano diversi.
Gli indiani concepirono probabilmente la notazione posizionale nel I secolo, ma la prima prova documentaria databile per la notazione posizionale risale al 594. La testimonianza è un documento legale che porta la data 346 nel calendario chedii, ma alcuni studiosi credono che la data sia un falso. Nonostante questo, c’è un generale accordo sul fatto che la notazione posizionale fosse in uso in India a partire dal 400.
Sorge un problema usando solo i simboli da 1 a 9: la notazione è ambigua. Che cosa significa 25, per esempio? Potrebbe significare (nella nostra notazione) 25, oppure 205, oppure 2005, oppure 250 e così via. Nella notazione posizionale, in cui il significato di un simbolo dipende dalla sua posizione, è importante specificare quella posizione senza ambiguità. Oggi lo facciamo usando un decimo simbolo, lo zero (0). Passò però molto tempo prima che le antiche civiltà riconoscessero il problema e lo risolvessero in questo modo. C’era una motivazione filosofica: come può 0 essere un numero se un numero è una quantità di cose? Il nulla è una quantità? Vi era un’altra ragione di ordine pratico: in genere era chiaro dal contesto se 25 significava 25 oppure 250 oppure qualche altro valore.
Poco tempo prima del 400 a. C., la data esatta non è nota, i babilonesi introdussero un simbolo speciale per indicare una posizione mancante nella loro notazione numerica. Questo risparmiò agli scribi la fatica di lasciare uno spazio opportuno, e rese possibile sapere che cosa rappresentava un numero anche se era scritto in maniera meno accurata. Questa invenzione fu abbandonata, o non trasmessa ad altre culture, ma alla fine fu riscoperta dagli indu. Il manoscritto di Bakhshali, la cui datazione è controversa ma collocabile tra il 200 e il 1100, usa un punto calcato •. Il testo gianista Lokavibhaaga, risalente al 458, usa il concetto di zero, ma non un simbolo. Un sistema posizionale privo del numerale zero fu introdotto da Āryabhata nel 500 circa. I matematici indiani successivi avevano nomi per lo zero, ma non usavano un simbolo. Il primo indiscusso uso dello zero in notazione posizionale compare su una tavoletta di pietra di Gwalior risalente all’anno 876.
Brahmagupta, Mahāvīra e Bhāskara
I principali matematici indiani furono Āryabhata (nato nel 476), Brahmagupta (nato nel 598), Mahāvīra (IX secolo) e Bhāskara (nato nel 1114). Di fatto dovrebbero essere definiti astronomi, perché a quei tempi la matematica era considerata una tecnica astronomica. La matematica esistente era esposta in alcuni capitoli nei testi di astronomia: non era considerata come materia a se stante.
Āryabhata racconta di aver scritto la sua opera Āryabhatiya all’età di ventitré anni. Per quanto breve, la parte matematica del libro contiene una messe di materiale: un sistema alfabetico dei numerali, regole aritmetiche, metodi di risoluzione per equazioni lineari e quadratiche, trigonometria (compresa la funzione seno e il «senoverso» 1 — cos θ). Troviamo anche un’eccellente approssimazione di π, come 3,1416.
Brahmagupta fu autore di due libri, Brahma Sphuta Siddhānta e Khanda Khādyaka. Il primo è il più importante: si tratta di un testo di astronomia con diversi capitoli di matematica, che contengono nozioni di aritmetica e l’equivalente letterale dell’algebra semplice. Il secondo volume include un metodo interessante per interpolare tavole di seni, vale a dire trovare il seno di un angolo dal seno di un angolo più ampio e di uno più piccolo.
Mahāvīra era un gianista, e inserì molta matematica gianista nel suo Ganita Sara Samgraha. Questo libro trattava la maggior parte degli argomenti trattati nei volumi di Āryabhata e Brahmagupta, ma si spingeva molto oltre ed era in genere più sofisticato. Comprendeva frazioni, permutazioni e combinazioni, la soluzione delle equazioni quadratiche, i triangoli pitagorici e un tentativo di trovare l’area e il perimetro di un’ellisse.
Bhaskara (conosciuto come «il maestro») scrisse tre opere importanti: Līlāvati, Bijaganita e Siddhānta Siromani. Secondo Fyzi, poeta di corte dell’imperatore moghul Akbar, Līlāvati era il nome della figlia di Bhāskara. Il padre ne aveva calcolato l’oroscopo, e aveva determinato la data più propizia per il matrimonio della ragazza. Per enfatizzare la sua previsione, aveva posto una tazza con un piccolo foro in un catino pieno d’acqua, facendo in modo che la tazza affondasse all’ora propizia. Līlāvati però si sporse sopra il catino, una perla del suo abito cadde nella tazza e otturò il foro. La tazza non andò a fondo, e questo significava che la ragazza non si sarebbe mai potuta sposare. Per tirarla su d’animo, Bhāskara scrisse per lei un manuale di matematica. La leggenda non riporta come l’abbia presa Līlāvati.
Quello che l’aritmetica fece per loro
Il testo cinese di matematica più antico giunto fino a noi è il Chiu Chang, che risale all’anno 100 circa. Un problema tipico è: due picul e mezzo di riso costano 3/7 di un tael d’argento. Quanti picul si possono acquistare con 9 tael? La soluzione proposta usa quella che i matematici medievali chiamavano la «regola del tre». Nella notazione moderna, indichiamo con x la quantità richiesta. Si ha
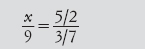
e quindi 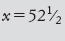 picul. Un picul equivale a
circa 65 chilogrammi.
picul. Un picul equivale a
circa 65 chilogrammi.
Līlāvati contiene sofisticate idee di aritmetica, compresa la regola del nove, in cui i numeri sono sostituiti dalla somma delle loro cifre per verificare i calcoli. Contiene regole simili per la divisibilità per 3, 5, 7 e 11. Il ruolo dello zero come numero è ben chiaro. Bijaganita tratta la soluzione di equazioni. Siddhānta Siromani affronta la trigonometria: tavole di seni e diverse relazioni trigonometriche. Così alta era la reputazione di Bhāskara che intorno al 1800 le sue opere erano ancora copiate.
Il sistema indù
Il sistema indù cominciò a espandersi nel mondo arabo, prima che fosse pienamente sviluppato nella sua regione d’origine. Nel 662, lo studioso Severus Sebokht fa riferimento all’uso dei numeri indiani in Siria: «Tralascerò ogni discussione sulla scienza degli indiani […] sulle loro raffinate scoperte in astronomia […] e sui loro preziosi metodi di calcolo […] desidero soltanto dire che questa operazione è effettuata con l’uso di nove simboli».
Nel 776 un viaggiatore proveniente dall’India si presentò alla corte del califfo e dimostrò la sua prodezza nell’eseguire operazioni secondo il metodo «siddhānta», nonché in trigonometria e astronomia. Sembra che alla base dei metodi di calcolo ci fosse il Brahma Sphuta Siddhānta di Brahmagupta, scritto nel 628, ma qualunque fosse il libro, fu prontamente tradotto in arabo.
In origine i numerali indù erano usati soprattutto dagli eruditi; i metodi precedenti restarono ampiamente in uso tra i commercianti arabi e nella vita quotidiana, fino all’anno 1000 circa. Nell’anno 825, però, l’opera di al-Khwārizmī, Sull’arte indiana dei calcoli, diffuse nel mondo arabo la conoscenza del sistema indù. Il trattato in quattro volumi di al-Kindī, Sull’uso dei numeri indiani, comparso nell’anno 830, valse ad accrescere la consapevolezza della possibilità di eseguire tutti i calcoli numerici usando soltanto le dieci cifre.
Secoli bui?
Mentre arabi e indiani facevano notevoli progressi in matematica e nelle scienze, al confronto in Europa la situazione era stagnante, anche se il periodo medievale non corrispose esattamente ai «secoli bui» come si ritiene in genere. Si ebbero alcuni progressi, ma furono lenti e non particolarmente significativi. Il ritmo cominciò ad accelerare quando giunse in Europa la notizia delle scoperte orientali. L’Italia si trova più vicina al mondo arabo rispetto alla maggior parte dell’Europa, e dunque era forse inevitabile che i progressi arabi in matematica facessero il loro ingresso in Europa attraverso l’Italia. Venezia, Genova e Pisa erano importanti centri commerciali, e i mercanti salpavano da questi porti diretti nell’Africa settentrionale e nelle regioni orientali del Mediterraneo. Vendevano lana e legno europeo in cambio di sete e spezie.
Accanto alle attività di commercio vero e proprio si ebbero anche scambi metaforici di idee. Le scoperte degli arabi in campo scientifico e matematico fecero il loro ingresso lungo le rotte commerciali, spesso con il passaparola. Mentre il commercio rendeva l’Europa più ricca, il baratto cedeva il passo alla moneta, e sia la contabilità che il pagamento delle tasse si fecero più complessi. L’equivalente dell’epoca di una calcolatrice tascabile era l’abaco, uno strumento in cui i numeri sono rappresentati da perline mobili lungo fili. In ogni caso, quei numeri dovevano poi essere scritti su carta, per scopi legali e per la contabilità generale. I mercanti avevano quindi bisogno di una notazione numerica efficiente e anche di metodi che permettessero di eseguire i calcoli in maniera rapida e accurata.

Figura 3.3
Evoluzione dei simboli numerici occidentali.
Un personaggio di spicco fu Leonardo Pisano, altrimenti noto come Fibonacci, il cui libro Liber abaci fu pubblicato nel 1202. (Il termine «abaco» indica l’arte di fare i conti, e non implica necessariamente l’uso di un abaco). In questo libro, Leonardo introduceva in Europa i simboli numerici indo-arabi.
Il Liber abaci presenta, e raccomanda,
un altro strumento di notazione che è usato ancora oggi: la riga
orizzontale in una frazione, come 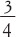 per «tre quarti». Gli
indù utilizzavano una notazione simile, ma senza la riga, che
sembra sia stata introdotta dagli arabi. Fibonacci la usò
ampiamente, ma per certi aspetti in maniera diversa rispetto a come
facciamo oggi. Per esempio, egli avrebbe usato la stessa riga come
parte di varie frazioni differenti.
per «tre quarti». Gli
indù utilizzavano una notazione simile, ma senza la riga, che
sembra sia stata introdotta dagli arabi. Fibonacci la usò
ampiamente, ma per certi aspetti in maniera diversa rispetto a come
facciamo oggi. Per esempio, egli avrebbe usato la stessa riga come
parte di varie frazioni differenti.
Dal momento che le frazioni sono molto importanti
nella nostra storia, può essere utile aggiungere qualche commento
sulla notazione. In una frazione come 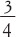 , il 4 in basso ci
dice di dividere l’unità in quattro parti uguali, e il 3 sopra ci
dice di prendere tre di quelle parti. In termini più formali, 4 è
il denominatore e 3 è il numeratore. Per convenienza tipografica, le frazioni sono spesso
scritte su un’unica riga come 3/4, o talvolta con la forma
intermedia ¾. La riga orizzontale in questo caso si trasforma in
una barra diagonale.
, il 4 in basso ci
dice di dividere l’unità in quattro parti uguali, e il 3 sopra ci
dice di prendere tre di quelle parti. In termini più formali, 4 è
il denominatore e 3 è il numeratore. Per convenienza tipografica, le frazioni sono spesso
scritte su un’unica riga come 3/4, o talvolta con la forma
intermedia ¾. La riga orizzontale in questo caso si trasforma in
una barra diagonale.
Leonardo Pisano (Fibonacci) (1170-1250)
Leonardo nacque in Italia ma trascorse l’infanzia in Africa settentrionale, dove il padre Guglielmo era diplomatico al servizio dei mercanti che commerciavano a Bugia (l’odierna Algeria). Seguì il padre nei suoi numerosi viaggi, ebbe modo di conoscere il sistema arabo di scrittura dei numeri e ne comprese l’importanza. Nel suo Liber abaci del 1202 scrive:
Quando mio padre, che era stato nominato dal suo paese notaio della clientela a Bugia, per operare a favore dei mercanti pisani che si recavano là, fu in carica, mi chiamò con lui, quando ero appena un bambino, e, siccome aveva occhio per i vantaggi e le future convenienze, decise che io dovessi stare là e che ricevessi un’istruzione nella scuola di ragioneria. Qui, mi venne insegnata l’arte dei nove simboli indiani, attraverso notevoli insegnamenti e, presto, la conoscenza dell’arte mi piacque più di ogni altra cosa.
Il libro introdusse in Europa la notazione indo-araba, e rappresentò un esauriente testo di aritmetica, poiché includeva moltissimo materiale utile per questioni commerciali e per la conversione delle valute. Anche se furono necessari diversi secoli prima che la notazione indoaraba soppiantasse il tradizionale abaco, i vantaggi di un sistema di calcolo basato soltanto sulla scrittura furono presto evidenti.
Leonardo è anche conosciuto con il soprannome di Fibonacci, che significa «figlio di Bonacci», ma questo appellativo non si trova prima del XVIII secolo, e fu probabilmente inventato allora da Guglielmo Libri.
Nel complesso, tuttavia, noi raramente usiamo la notazione frazionale nelle attività pratiche. In genere usiamo i decimali, scrivendo π come 3,14159, per esempio, che non rappresenta il valore esatto, ma una buona approssimazione per la maggior parte dei calcoli. Dal punto di vista storico, dobbiamo fare un piccolo salto per giungere ai decimali, ma stiamo seguendo il filo delle idee, e non la cronologia, e comunque sarà molto più semplice fare il salto. Balziamo dunque in avanti fino al 1585, quando Guglielmo il Taciturno scelse l’olandese Simone Stevino come istitutore privato per il figlio Maurizio di Nassau.
Partendo da questo incarico, Stevino fece presto carriera, diventando ingegnere delle dighe, generale dell’esercito e infine ministro delle finanze. Stevino comprese presto la necessità di metodi accurati per la contabilità, e studiò gli aritmetici italiani del Rinascimento, e la notazione indo-araba introdotta in Europa da Leonardo Pisano. Trovò poco pratici i calcoli con le frazioni, e avrebbe preferito la precisione e l’ordine dei sessagesimali babilonesi, se non fosse per l’uso della base 60. Tentò di mettere a punto un sistema che combinasse il meglio di entrambi, e ne inventò uno in base 10 analogo a quello dei babilonesi: il sistema decimale.
Pubblicò il suo nuovo sistema di notazione, mettendo in chiaro che era stato provato, verificato e riconosciuto come assolutamente pratico da uomini assolutamente pratici. Ne sottolineò inoltre la validità come strumento commerciale: «tutti i calcoli necessari nelle attività commerciali possono essere eseguiti con interi soltanto senza l’uso di frazioni».
La sua notazione non prevede il punto decimale a
noi familiare, ma conduce molto rapidamente alla notazione decimale
moderna. Dove noi scriveremmo 5,7731, per esempio, Stevino
scriverebbe 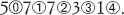 Il simbolo
Il simbolo  indica un numero intero,
indica un numero intero,  indica un decimo,
indica un decimo,  un
centesimo e così via. Con il passare del tempo il sistema entrò
nelle abitudini; vennero omessi i simboli
un
centesimo e così via. Con il passare del tempo il sistema entrò
nelle abitudini; vennero omessi i simboli  ,
,  ecc., ma si continuò a scrivere lo
ecc., ma si continuò a scrivere lo  , che contratto e
semplificato divenne poi il familiare punto decimale.
, che contratto e
semplificato divenne poi il familiare punto decimale.
Numeri negativi
I matematici identificano il sistema dei numeri interi non negativi con l’espressione numeri naturali. Includendo anche i numeri negativi, otteniamo gli interi. I numeri razionali (o semplicemente i «razionali») sono le frazioni positive e negative, i numeri reali (o semplicemente «reali») sono i decimali positivi e negativi, procedendo all’infinito se necessario.
Come entrano nella storia i numeri negativi?
Figura 3.4
Antiche bacchette cinesi da calcolo.
A partire dal primo millennio, i cinesi usavano un sistema di «bacchette da calcolo» al posto dell’abaco. Disponevano le bacchette in una certa configurazione per rappresentare i numeri.
Nella figura 3.4, la riga superiore mostra bacchette heng, che rappresentano unità, centinaia, decine di migliaia e così via, a seconda della posizione occupata in una fila di simboli simili. La riga inferiore mostra bacchette tsung, che rappresentano decine, migliaia e così via. I due tipi di bacchette quindi si alternano. I calcoli erano eseguiti spostando le bacchette secondo un metodo stabilito.
Per risolvere un sistema di equazioni lineari, i contabili cinesi disponevano le bacchette in una specie di tabella (la tavola da calcolo aritmetica, quadrettata). Usavano bacchette rosse per i termini da sommare e bacchette nere per i termini da sottrarre, e quindi per risolvere il sistema di equazioni che, nella nostra notazione moderna, sarebbe scritto come
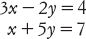
rappresentavano le due equazioni come le due colonne di una tabella: una con i numeri 3 (rosso), 2 (nero), 4 (rosso), e l’altra con 1 (rosso), 5 (rosso), 7 (rosso).
La notazione rosso/nero non indicava proprio i numeri negativi, ma l’operazione di sottrazione, e in ogni caso poneva le basi per il concetto dei numeri negativi, cheng fu shu. Un numero negativo era quindi rappresentato aggiungendo una bacchetta in diagonale sopra il numero positivo corrispondente.
Per Diofanto, tutti i numeri dovevano essere positivi, tanto che egli rifiutava le soluzioni negative delle equazioni. I matematici indù ritenevano i numeri negativi utili per rappresentare i debiti nei calcoli contabili: essere debitori di una somma di denaro era peggio, dal punto di vista finanziario, rispetto a non avere denaro, e dunque un debito doveva chiaramente essere minore di zero. Se abbiamo 3 euro e ne sborsiamo 2, rimaniamo con 3 − 2 = 1. Per lo stesso motivo, se abbiamo un debito di 2 euro e ne guadagnamo 3, il patrimonio totale è −2 + 3 = 1. Bhāskara osserva che un particolare problema ha due soluzioni, 50 e −5, ma rimane turbato dalla seconda soluzione, dicendo che «non è da considerare, perché le persone non approvano soluzioni negative».
Nonostante questi dubbi, i numeri negativi furono accettati. La loro interpretazione, in un calcolo reale, richiede attenzione. Talvolta non hanno senso, talvolta possono essere debiti, talvolta possono significare un movimento verso il basso al posto di uno verso l’alto. A parte l’interpretazione però, la loro aritmetica funziona benissimo, e furono talmente utili nei calcoli che sarebbe stato sciocco non usarli.

Figura 3.5
Sistema cinese di rappresentazione delle equazioni. Le bacchette chiare sono rosse.
L’aritmetica sopravvive
Il nostro sistema numerico ci è così familiare che in genere diamo per scontato che sia l’unico possibile, o almeno l’unico sensato. In realtà, esso si è evoluto, faticosamente e con moltissimi vicoli ciechi, nel corso di migliaia di anni. Esistono molte alternative: alcune furono usate da culture precedenti, come i maya. Notazioni diverse per i numeri da 0 a 9 sono in uso oggi in alcuni paesi. E i nostri computer rappresentano i numeri nei loro codici interni con il sistema binario, non decimale: i loro programmatori garantiscono che i numeri siano convertiti nel sistema decimale prima di comparire sullo schermo o in una stampa.
Quello che l’aritmetica fa per noi
Noi usiamo l’aritmetica in tutte le nostre attività quotidiane, nel commercio e nella scienza. Fino allo sviluppo delle calcolatrici elettroniche e dei computer, eravamo soliti eseguire i calcoli a mano, con carta e penna, oppure con l’aiuto di strumenti come l’abaco o il prontuario contabile (un libro pieno di tabelle di multipli di quantità di denaro). Oggi la maggior parte dell’aritmetica gira su dispositivi elettronici dietro le quinte: i registratori di cassa dicono al cassiere quanto resto dare al cliente, per esempio, mentre le banche calcolano in automatico il saldo del vostro conto corrente, e non lo fanno fare ai loro contabili. La quantità di aritmetica «consumata» da una persona media durante una giornata è notevole.
Sui computer i calcoli aritmetici non sono eseguiti in formato decimale. I computer usano il sistema in base 2, o binario, e non il sistema in base 10. Al posto di unità, decine, centinaia, migliaia e così via, i computer usano 1, 2, 4, 8, 16, 32, 64, 128, 256, e così via: le potenze di due, ogni valore doppio del precedente. (Ecco perché la scheda di memoria della vostra macchina fotografica digitale può avere una dimensione strana come 256 megabytes). In un computer, il numero 100 sarebbe scomposto come 64 + 32 + 4 e memorizzato nella forma 1100100.
Numerali maya
Un sistema numerico degno di nota, che usava la notazione in base 20 e non in base 10, fu concepito dai maya, che vissero nell’America meridionale intorno all’anno 1000. Nel sistema in base 20, i simboli equivalenti al nostro 347 significherebbero
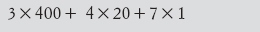
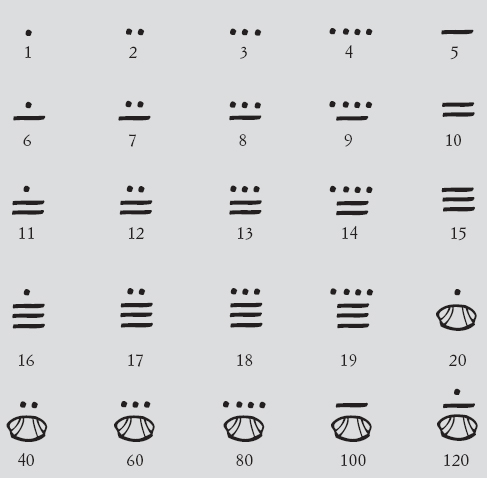
(poiché 20 × 20 = 400), che equivale a 1287 nella nostra notazione. I simboli usati sono mostrati nell’immagine.
Le prime civiltà che adottarono un sistema in base 10 fecero probabilmente riferimento alle dieci dita delle mani dell’uomo. Per spiegare perché i maya avessero adottato un sistema in base 20, si è ipotizzato che contassero anche con le dita dei piedi.
Dal momento che i computer sono ora onnipresenti, ha qualche senso insegnare ancora l’aritmetica? Certo, per molte ragioni. Ci vuole qualcuno che sia in grado di progettare e costruire le calcolatrici e i computer, di farli operare correttamente, e questo richiede la comprensione dell’aritmetica: sapere come e perché funziona, non soltanto come effettuare operazioni. E se la nostra unica capacità aritmetica è quella di leggere il risultato che compare sullo schermo di una calcolatrice, probabilmente non ci accorgiamo se il conto del supermercato è sbagliato. Se non comprendiamo appieno le operazioni fondamentali dell’aritmetica, l’intero corpus della matematica sarà per noi inaccessibile. Non dobbiamo preoccuparci di questo, ma la civiltà moderna crollerebbe presto se smettessimo di insegnare l’aritmetica, perché non possiamo distinguere i futuri ingegneri e scienziati all’età di cinque anni. E neppure i futuri banchieri e ragionieri.
Naturalmente, una volta che abbiamo una buona dimestichezza con le basi dell’aritmetica, una calcolatrice è utile per risparmiare tempo e fatica, ma, proprio come non possiamo imparare a camminare sostenuti sempre da una stampella, non possiamo imparare a riflettere seriamente sui numeri affidandoci sempre a una calcolatrice.