13.
La nascita della simmetria
Come non risolvere un’equazione
Intorno al 1850 la matematica subì una delle trasformazioni più significative di tutta la sua storia, anche se all’epoca questo non fu così evidente. Prima del 1800, gli oggetti di studio principali della matematica erano abbastanza concreti: numeri, triangoli, sfere. L’algebra usava le formule per rappresentare le operazioni con i numeri, ma le formule in quanto tali erano viste come rappresentazioni simboliche di processi, non come oggetti di per sé. Dal 1900 invece le formule e le trasformazioni furono viste come oggetti, non come processi, e gli oggetti dell’algebra diventarono molto più astratti e generali. Di fatto, non andava bene quasi nulla per l’algebra. Anche le leggi fondamentali, come la proprietà commutativa della moltiplicazione, ab = ba, erano messe da parte in alcune aree importanti.
Teoria dei gruppi
Queste trasformazioni si verificarono soprattutto perché i matematici scoprirono la teoria dei gruppi, un’area della matematica nata da alcuni tentativi infruttuosi di risolvere equazioni algebriche, soprattutto quella di quinto grado. A distanza di cinquant’anni dalla sua scoperta però, la teoria dei gruppi è stata riconosciuta come il contesto giusto per studiare il concetto di simmetria. Quando i nuovi metodi furono accolti dalla coscienza collettiva, divenne chiaro che la simmetria è un’idea profonda e centrale, con innumerevoli applicazioni alle scienze fisiche, anche a quelle biologiche. Oggi, la teoria dei gruppi è uno strumento indispensabile in ogni area della matematica e della scienza, e le sue connessioni con la simmetria sono messe in evidenza nella maggior parte dei testi introduttivi. Lo sviluppo di questa concezione richiese però diversi decenni. Intorno al 1900 Henri Poincaré affermò che la teoria dei gruppi rappresentava di fatto tutta la matematica ridotta ai suoi concetti essenziali: un punto di vista forse esagerato, ma sostenibile.
Il punto di svolta nell’evoluzione della teoria dei gruppi venne dal lavoro di un giovane francese, Évariste Galois. La storia precedente era stata lunga e complicata: le idee di Galois non nascevano dal nulla. E la storia successiva fu pure ugualmente complicata e spesso anche confusa, soprattutto quando i matematici sperimentarono i nuovi concetti, e tentarono di distinguere quelli importanti da quelli che non lo erano. Fu però Galois, più di ogni altro, che comprese chiaramente la necessità dei gruppi, ne definì alcune caratteristiche fondamentali, e ne dimostrò l’importanza centrale nella matematica. Non sorprende affatto che il suo lavoro sia stato quasi ignorato quand’egli era in vita. Era forse un po’ troppo originale, ma va detto che la personalità di Galois e il suo fiero coinvolgimento nella politica rivoluzionaria non furono di aiuto. Fu un personaggio tragico che visse in un periodo costellato di tragedie personali; la sua è una delle storie più drammatiche, e forse romantiche, tra quelle di tutti i grandi matematici.
Risolvere equazioni
La storia della teoria dei gruppi risale direttamente agli antichi lavori dei babilonesi sulle equazioni quadratiche. Per quanto interessava ai babilonesi, il loro metodo aveva fini pratici: era una tecnica di calcolo, e molto probabilmente non si erano posti altre questioni più profonde in merito. Se sapevi come calcolare le radici quadrate, e padroneggiavi l’aritmetica elementare, eri in grado di risolvere le quadratiche.
Le tavolette di argilla giunte fino a noi suggeriscono in qualche modo che i babilonesi conoscessero anche le equazioni cubiche, e addirittura alcune equazioni quartiche. I greci, e gli arabi dopo di loro, avevano scoperto metodi geometrici, basati sulle sezioni coniche, per risolvere le equazioni cubiche. (Noi ora sappiamo che le tradizionali circonferenze e rette di Euclide non possono risolvere esattamente problemi di questo genere. Era necessario qualcosa di più sofisticato, e guarda caso le coniche hanno i requisiti giusti). Una delle figure più importanti in questo campo fu il persiano Omar Khayyam. Omar risolse tutti i tipi possibili di cubiche con metodi geometrici sistematici. Come abbiamo visto però, una soluzione algebrica delle equazioni cubiche e quartiche dovette attendere fino al Rinascimento, con gli studi di del Ferro, Tartaglia, Fior, Cardano e del suo allievo Ferrari.
Le simmetrie di una quadratica
Consideriamo un’equazione quadratica, nella forma leggermente semplificata
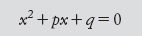
Supponiamo che le due soluzioni siano x = a e x = b
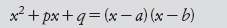
Questo ci dice allora che

Anche se quindi non conosciamo ancora le soluzioni, ne conosciamo la somma e il prodotto, senza grande fatica.
Perché è così? La somma a + b è uguale a b + a, e quindi non cambia se le soluzioni sono permutate. Lo stesso vale per ab = ba. Si ha che ogni funzione simmetrica delle soluzioni può essere espressa in termini dei coefficienti p e q. Inversamente, ogni espressione in p e q è sempre una funzione simmetrica di a e b. In generale, la relazione tra le soluzioni e i coefficienti è determinata da una proprietà di simmetria.
Le funzioni asimmetriche non si comportano in questo modo. Un buon esempio è la differenza a − b. Se scambiamo a e b, la differenza diventa b − a che dà un risultato diverso. Ad ogni modo, e questa è un’osservazione fondamentale, il risultato non è molto diverso. È quello che otteniamo da a − b cambiando il segno. Il quadrato (a − b)2 è quindi assolutamente simmetrico. Ogni funzione completamente simmetrica delle soluzioni deve però essere una certa espressione contenente i coefficienti. Calcoliamo la radice quadrata, e abbiamo espresso a − b in termini dei coefficienti, usando niente di più esoterico di una radice quadrata. Conosciamo già il valore di a + b, che è uguale a −p. Poiché conosciamo anche a − b, la somma di questi due numeri è 2a e la differenza è 2b. Dividendo per 2, otteniamo formule per a e per b.
Quello che abbiamo fatto è dimostrare che deve esistere una formula per le soluzioni a e b che non richiede nulla di più strano di una radice quadrata, sulla base di proprietà generali delle simmetrie delle espressioni algebriche. Questo è straordinario: abbiamo dimostrato che il problema ha una soluzione, senza doverci occupare di calcolare tutti i complicati dettagli che ci dicono quale sia. In un certo senso, abbiamo scoperto perché i babilonesi furono in grado di trovare un metodo. Questo piccolo racconto getta nuova luce sul termine «capire». Possiamo capire come il metodo babilonese fornisce una soluzione, esaminando i diversi passaggi e verificando la logica. Ora però, abbiamo capito perché un metodo del genere doveva esistere, non presentando una soluzione, ma esaminando le proprietà generali delle soluzioni presunte. In questo caso, la proprietà fondamentale si rivelò la simmetria.
Con un po’ più di fatica, arrivando a un’espressione esplicita per (a − b)2, questo metodo fornisce una formula per le soluzioni. È equivalente alla formula che abbiamo imparato a scuola, e al metodo usato dai babilonesi.
Da tutto questo lavoro sembrava emergere un quadro semplice, anche se confuso nei dettagli. Puoi risolvere qualunque cubica usando le operazioni aritmetiche, più le radici quadrate, più le radici cubiche. Puoi risolvere qualunque quartica usando le operazioni aritmetiche, più le radici quadrate, più le radici cubiche, più le radici di quarto grado, anche se le ultime possono essere ridotte a due radici quadrate in successione. Sembrava ragionevole pensare di poter proseguire questo schema, in modo da poter risolvere ogni equazione di quinto grado usando le operazioni aritmetiche più le radici quadrate, le radici cubiche, le radici di quarto e quinto grado. E via così, per risolvere equazioni di ogni grado. Senza dubbio le formule sarebbero state molto complicate, ma alcuni sembravano dubitare della loro esistenza.
Con il passare dei secoli, senza trovare alcun indizio circa la possibilità di tali formule, alcuni eminenti matematici decisero di studiare il problema con maggiore attenzione, per capirne la vera essenza, unificare i metodi conosciuti e semplificarli in modo da capire bene perché funzionavano. Allora, pensavano, sarebbe bastato applicare gli stessi principi generali, e l’equazione di quinto grado avrebbe svelato il suo segreto.
Il lavoro più riuscito e sistematico in questa direzione fu condotto da Lagrange, il quale reinterpretò le formule classiche in termini delle soluzioni cercate. Quello che era importante, egli affermava, era il comportamento di certe particolari espressioni algebriche contenenti quelle soluzioni, quando le soluzioni stesse erano permutate, cioè disposte in ordine diverso. Egli sapeva che ogni espressione completamente simmetrica (che rimane sempre uguale, indipendentemente da come le soluzioni siano permutate) si poteva rappresentare in termini dei coefficienti dell’equazione, rendendola una quantità nota. Più interessanti erano le espressioni che assumevano soltanto pochi valori diversi quando si permutavano le soluzioni, perché in esse sembrava nascosta la chiave di tutto quello che riguardava la soluzione delle equazioni.
Lagrange aveva una raffinata sensibilità per la bellezza della forma matematica, e intuì che questa fosse una grande idea. Se era possibile sviluppare qualcosa del genere per le equazioni cubiche e quartiche, allora Lagrange poteva scoprire come risolvere le equazioni di quinto grado.
Applicando lo stesso principio fondamentale, scoprì che usando funzioni parzialmente simmetriche delle soluzioni poteva ridurre un’equazione cubica a un’equazione quadratica. La quadratica introduceva una radice quadrata, e il processo di riduzione si poteva completare usando una radice cubica. Analogamente, ogni equazione quartica poteva essere ridotta a una cubica, che egli chiamò risolvente cubica. Era quindi possibile risolvere una quartica usando radici quadrate e cubiche per trattare la risolvente cubica e radici di quarto grado per stabilire una relazione tra la risposta e le soluzioni richieste. In entrambi i casi, le risposte erano identiche alle formule classiche del Rinascimento. Doveva essere così, naturalmente: quelle erano le risposte. Ora però Lagrange sapeva perché quelle erano le risposte, e meglio ancora, sapeva perché esistevano delle risposte da trovare.
Lagrange doveva essere abbastanza esaltato in questa fase della sua ricerca. Se consideriamo l’equazione di quinto grado, e applichiamo le stesse tecniche, ci aspettiamo di ottenere una risolvente quartica: fine del lavoro. Lagrange però, forse con disappunto, non ottenne una risolvente quartica, ma una risolvente sestica, cioè un’equazione di sesto grado.
Invece di rendere le cose più semplici, il suo metodo rendeva l’equazione di quinto grado più complicata.
C’era un errore nel metodo? Poteva un
procedimento magari più ingegnoso risolvere l’equazione di quinto
grado? Sembra che Lagrange ne fosse convinto. Come scrisse, sperava
che la sua nuova impostazione fosse utile a chiunque tentasse di
sviluppare un metodo per risolvere le equazioni di quinto grado.
Forse non gli era venuto in mente che un metodo siffatto poteva non
esistere, e che la sua impostazione falliva in generale,
perché le equazioni di quinto grado non hanno soluzioni
espresse come «radicali», che sono espressioni che implicano
operazioni aritmetiche e diverse radici, come quelle di quinto
grado. Per confondere le cose, alcune equazioni di quinto
grado hanno soluzioni di questo tipo, per esempio
x5 − 2 = 0 ha la soluzione 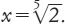 Questo però è
un caso piuttosto semplice, e per niente particolare.
Questo però è
un caso piuttosto semplice, e per niente particolare.
Tutte le equazioni di quinto grado hanno soluzione, per inciso; in generale si tratta di numeri complessi, che possono essere trovati con metodi numerici e con la precisione voluta. Il problema riguardava le formule algebriche utili per trovare le soluzioni.
La ricerca di una soluzione
Mentre le idee di Lagrange cominciavano ad affermarsi, si diffuse sempre più il timore di non riuscire a risolvere il problema. Forse l’equazione di quinto grado generica non poteva essere risolta con i radicali. Sembra che Gauss la pensasse in questo modo, in cuor suo, ma dichiarò che secondo lui si trattava di un problema che non valeva la pena affrontare. È forse uno dei pochi casi in cui Gauss fu abbandonato dal suo fiuto nell’intuire l’importanza di una questione. Accadde lo stesso con l’ultimo teorema di Fermat, ma in questo caso i metodi necessari superavano anche le capacità di Gauss, e richiesero circa due secoli per delinearsi. Ironia della sorte, però, Gauss aveva già cominciato a sviluppare parte dell’algebra necessaria per dimostrare l’impossibilità di risolvere l’equazione di quinto grado. L’aveva introdotta nel lavoro in cui trattava la costruzione dei poligoni regolari con riga e compasso, e aveva anche, nello stesso lavoro, posto un precedente, dimostrando (per propria soddisfazione, in ogni caso) che alcuni poligoni non potevano essere costruiti in quel modo. Il poligono regolare a nove lati era un esempio. Gauss lo sapeva, ma non sviluppò mai una dimostrazione; qualche tempo dopo ne venne una da Pierre Wantzel. Gauss aveva quindi stabilito un precedente in merito al fatto che alcuni problemi non potessero essere risolti con determinati metodi.
Il primo a tentare una dimostrazione dell’insolubilità fu Paolo Ruffini, che divenne professore di matematica all’Università di Modena nel 1789. Portando avanti le idee di Lagrange sulle funzioni simmetriche, Ruffini si convinse che non esisteva alcuna formula, contenente nulla di più esoterico delle radici n-esime, per risolvere l’equazione di quinto grado. Nella sua Teoria generale delle equazioni del 1799 sosteneva una dimostrazione del fatto che «la soluzione algebraica delle equazioni generali di grado superiore al quarto è sempre impossibile». La dimostrazione era però così lunga (500 pagine) che nessuno ebbe voglia di verificarla, soprattutto dopo che si diffuse il sospetto che contenesse alcune imprecisioni. Nel 1803 Ruffini pubblicò una nuova dimostrazione semplificata, che non ebbe comunque maggiore fortuna. Per tutta la vita, Ruffini non riuscì mai a farsi attribuire il merito di aver dimostrato l’impossibilità di risolvere l’equazione di quinto grado.
Il contributo più importante di Ruffini è quello di aver capito che le permutazioni si possono combinare tra loro. Fino ad allora, una permutazione era una configurazione di un certo insieme di simboli. Per esempio, se numeriamo le radici di un’equazione di quinto grado come 12345, allora questi simboli possono essere disposti come 54321, oppure 42153, oppure 23154, o ancora diversamente. Esistono 120 configurazioni possibili. Il trucco consisteva nel confrontare l’ordine originario 12345 con quello modificato. Solo a titolo di esempio, supponiamo che il nuovo ordine sia 54321. La regola per ottenere il nuovo ordine da quello iniziale era semplice: invertire l’ordine. Possiamo però invertire l’ordine di qualunque successione di cinque simboli. Se i simboli sono abcde, l’ordine inverso è edcba. Se i simboli sono disposti inizialmente come 23451, allora l’inversione dà 15432. Questo nuovo modo di vedere una permutazione implica la possibilità di effettuare due permutazioni successive, cioè una specie di moltiplicazione di permutazioni. L’algebra delle permutazioni, moltiplicate in questo modo, nasconde la soluzione del segreto dell’equazione di quinto grado.
Abel
Ora sappiamo che la dimostrazione di Ruffini conteneva un errore tecnico, ma le idee fondamentali sono valide e la lacuna può essere colmata. Ruffini ottenne un risultato: il suo libro contribuì a diffondere la vaga sensazione che l’equazione di quinto grado non fosse risolvibile per mezzo di radicali. Pochi pensavano che Ruffini l’avesse dimostrato, ma i matematici cominciarono a dubitare dell’esistenza di una soluzione. Purtroppo la conseguenza principale di questa convinzione fu quella di dissuadere chiunque dal dedicarsi al problema.
Fece eccezione Abel, un giovane norvegese con un talento precoce per la matematica, il quale pensò di aver risolto l’equazione di quinto grado quando era ancora studente. Alla fine scoprì un errore, ma rimase affascinato dal problema, e continuò a studiarlo a riprese successive. Nel 1823 trovò una dimostrazione dell’impossibilità di risolvere l’equazione di quinto grado, che era assolutamente corretta. Abel adottò una strategia simile a quella di Ruffini, ma la sua tattica si rivelò più efficace. All’inizio non sapeva delle ricerche di Ruffini; è chiaro che in seguito le conosceva, ma ne sostenne l’incompletezza. Abel non individuò però un problema particolare nella dimostrazione di Ruffini. È curioso notare che un passaggio della dimostrazione di Abel è proprio quello che mancava per colmare la lacuna in quella di Ruffini.
Possiamo avere un’idea generale dei metodi di Abel senza entrare in dettagli troppo tecnici. Egli impostò il problema distinguendo due tipi di operazione algebrica. Supponiamo di partire con diverse quantità, che possono essere numeri specifici oppure espressioni algebriche con diverse incognite. Da queste possiamo costruire molte altre quantità. Il modo semplice per farlo è combinare le quantità esistenti sommandole, sottraendole, moltiplicandole o dividendole. A partire da una semplice incognita, x, possiamo dunque creare espressioni come x2, 3x + 4, oppure (x + 7)/(2x − 3). Dal punto di vista algebrico, tutte queste espressioni sono pressoché equivalenti alla stessa x.
Il secondo modo per ottenere nuove quantità da quelle esistenti prevede l’introduzione di radicali. Si prenda un’innocua combinazione delle quantità esistenti, di quelle viste prima, e se ne estragga qualche radice. Definiamo questo passo come l’aggiunta di un radicale. Se è una radice quadrata, diciamo che il grado del radicale è 2, se è una radice cubica, allora il grado è 3, e così via.
In questi termini, la formula di Cardano per la cubica può essere riassunta come il risultato di un procedimento in due passaggi. Si parte con i coefficienti della cubica (e qualunque innocua combinazione di questi). Si aggiunge un radicale di grado 2. Si aggiunge poi un altro radicale di grado 3. Fatto! Questa descrizione ci dice quale tipo di formula si ottiene, ma non esattamente quale formula. Spesso la chiave per rispondere a un enigma matematico non consiste nel concentrarsi sui minimi particolari, ma nell’osservare le caratteristiche generali. Meno può significare di più. Quando funziona, questo stratagemma è spettacolare, e in questo caso funzionò egregiamente. Permise ad Abel di ridurre qualunque ipotetica formula per la soluzione dell’equazione di quinto grado ai suoi passaggi essenziali: estrarre una certa successione di radicali, in un determinato ordine, di gradi diversi. È sempre possibile fare in modo che i gradi siano primi: per esempio, una radice di sesto grado è la radice cubica di una radice quadrata.
Una successione del genere si dice torre radicale. Un’equazione è risolvibile per radicali se almeno una delle sue soluzioni può essere espressa da una torre radicale. Invece di imbarcarsi nella ricerca di una torre radicale, però, Abel assunse semplicemente che una torre radicale esistesse, e si chiese come doveva essere l’equazione originaria.
Senza accorgersene, Abel colmava così la lacuna della dimostrazione di Ruffini. Egli dimostrò che ogni volta che un’equazione può essere risolta per radicali, deve esistere una torre radicale che porta a quella soluzione, contenente soltanto i coefficienti dell’equazione originaria. Questo risultato è detto teorema sulle irrazionalità naturali e afferma che nulla si può ottenere includendo un intero insieme di nuove quantità, senza relazione con i coefficienti originari. Questo potrebbe sembrare ovvio, ma Abel comprese che è in molti casi il passaggio cruciale nella dimostrazione.
La chiave della dimostrazione di impossibilità di Abel è un astuto risultato preliminare. Supponiamo di considerare qualche espressione nelle soluzioni x1, x2, x3, x4, x5 dell’equazione, e di estrarne la p-esima radice per un certo numero primo p. Assumiamo inoltre che l’espressione originaria sia invariata quando applichiamo due permutazioni speciali
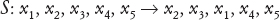
e
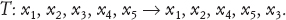
Allora, come Abel dimostrò, la p-esima radice di quell’espressione è anche invariata quando applichiamo S e T. Questo risultato preliminare conduce direttamente alla dimostrazione del teorema di impossibilità, «scalando la torre» gradino dopo gradino. Se assumiamo che l’equazione di quinto grado sia risolvibile per radicali, allora esiste una torre radicale che parte con i coefficienti e si inerpica fino a una soluzione.
Il primo piano della torre (l’innocua espressione contenente i coefficienti) è invariata quando applichiamo le permutazioni S e T, perché queste permutano le soluzioni, non i coefficienti. Pertanto, per il risultato preliminare di Abel, il secondo piano della torre è anche invariato quando applichiamo S e T, perché vi si arriva aggiungendo una radice p-esima di qualcosa al piano terreno, per un certo primo p. Con lo stesso ragionamento, il terzo piano della torre è invariato quando applichiamo S e T. Lo stesso vale per il quarto piano, il quinto… fino al piano più alto.
Ad ogni modo, il piano più alto contiene qualche soluzione dell’equazione. Potrebbe essere x1? In questo caso, allora x1 deve rimanere invariato quando applichiamo S. Se però applichiamo S a x1 otteniamo x2, e questo non va bene. Per ragioni simili, talvolta usando T, la soluzione definita dalla torre non può essere né x2, né x3, né x4, né x5. Tutte e cinque le soluzioni sono escluse da una torre di questo tipo, e dunque l’ipotetica torre non può, di fatto, contenere una soluzione.
Non c’è scampo a questa trappola logica. L’equazione di quinto grado non è risolvibile perché qualunque soluzione (per radicali) deve avere proprietà autocontraddittorie, e quindi non può esistere.
Galois
Lo studio non soltanto dell’equazione di quinto grado, ma di tutte le equazioni algebriche, fu poi portato avanti da Évariste Galois, uno dei personaggi più tragici nella storia della matematica. Galois si era prefisso l’obiettivo di determinare quali equazioni potevano essere risolte per radicali, e quali no. Come molti dei suoi predecessori, aveva compreso che la chiave per la soluzione algebrica delle equazioni era da cercare nel comportamento delle soluzioni in seguito a una permutazione. Si trattava di un problema di simmetria.
Ruffini e Abel avevano capito che un’espressione contenente le soluzioni non doveva necessariamente essere simmetrica oppure no. Poteva essere parzialmente simmetrica: invariata per alcune permutazioni ma non per altre. Galois notò che le permutazioni che soddisfano una certa espressione nelle radici non formano alcun insieme noto, e hanno una semplice e particolare proprietà: se consideriamo due permutazioni qualsiasi che soddisfano l’espressione, e le moltiplichiamo insieme, anche il risultato soddisfa l’espressione. Abel definì gruppo un insieme di permutazioni di questo tipo. Una volta compreso che questo risultato è vero, è molto facile dimostrarlo. La cosa importante è individuarlo, e riconoscerne il significato.
La conclusione del modello di Galois è che l’equazione di quinto grado non è risolvibile per radicali perché ha il tipo sbagliato di simmetria. Il gruppo di un’equazione di quinto grado generica consiste in tutte le permutazioni delle cinque soluzioni. La struttura algebrica di questo gruppo è incoerente con una soluzione per radicali.
Galois si dedicò a molte altre questioni matematiche, sempre ottenendo importanti scoperte. In particolare generalizzò l’aritmetica modulare per classificare quelli che ora chiamiamo campi di Galois. Si tratta di sistemi finiti in cui possono essere definite le operazioni aritmetiche di addizione, sottrazione, moltiplicazione e divisione, e si applicano tutte le leggi consuete. La dimensione di un campo di Galois è sempre una potenza di un numero primo, ed esiste esattamente un campo del genere per ogni potenza prima.
Évariste Galois era figlio di Nicholas-Gabriel Galois e Adelaide-Marie Demante. Crebbe nella Francia rivoluzionaria, e maturò idee politiche decisamente repubblicane. Il suo grande contributo alla matematica fu riconosciuto soltanto quattordici anni dopo la sua morte. La rivoluzione francese era iniziata con la presa della Bastiglia nel 1789 e l’esecuzione di Luigi XVI nel 1793. Nel 1804 Napoleone Bonaparte si era proclamato imperatore, ma dopo una serie di sconfitte militari era stato costretto ad abdicare. La monarchia era stata restaurata nel 1814 con Luigi XVIII. Nel 1824, Luigi era morto e il nuovo re era Carlo X.
Nel 1827 Galois cominciò a rivelare uno straordinario talento per la matematica (e anche un’ossessione). Cercò di entrare alla prestigiosa École Polytechnique, ma fallì l’esame di ammissione. Nel 1829 il padre, allora sindaco della cittadina di Bourg-la-Reine, si suicidò impiccandosi quando i suoi avversari politici inventarono uno scandalo fasullo. Poco dopo, Galois tentò nuovamente di essere ammesso all’École Polytechnique, ma fu di nuovo bocciato. Si iscrisse invece all’École Normale.
Nel 1830 Galois presentò le sue ricerche sulla soluzione delle equazioni algebriche per competere all’assegnazione di un premio offerto dall’Académie des sciences. L’esaminatore, Fourier, morì poco dopo, e l’articolo andò perduto. Il premio andò ad Abel (che allora era già morto di tubercolosi) e a Carl Jacobi. Nello stesso anno Carlo X fu deposto e fuggì per scampare alla morte. Il direttore dell’École Normale impedì ai propri studenti di uscire dal collegio per unirsi ai moti rivoluzionari. Galois, furioso, scrisse una lettera sarcastica in cui accusava il direttore di vigliaccheria, e fu immediatamente espulso.
Si raggiunse un compromesso, e salì al trono Luigi Filippo. Galois si unì a una milizia repubblicana, l’artiglieria della Guardia nazionale, ma il nuovo re l’abolì. Diciannove ufficiali della Guardia furono arrestati e processati per sedizione, ma la giuria fece cadere le accuse e la Guardia tenne una cena per festeggiare. Galois propose un brindisi ironico al re, brandendo in mano un coltello. Fu arrestato, ma assolto perché (come egli sostenne) il brindisi suonava come «A Luigi Filippo, se tradisce» e non come una minaccia di morte al re. Nella ricorrenza della presa della Bastiglia Galois fu però arrestato di nuovo, per aver indossato l’uniforme della Guardia, ormai illegale. In prigione, venne informato della sorte del suo articolo. Poisson lo aveva rifiutato perché poco chiaro. Galois tentò di uccidersi, ma gli altri prigionieri glielo impedirono. Il suo odio per la burocrazia si fece estremo, e manifestò segni di paranoia. Quando però si diffuse un’epidemia di colera, i prigionieri furono rilasciati.
A quel punto Galois si innamorò di una donna, il cui nome rimase un mistero per molti anni: pare si trattasse di Stephanie du Motel, la figlia del medico del posto. La relazione non fu felice, e Stephanie la interruppe. Uno dei compagni rivoluzionari di Galois lo sfidò allora a duello, apparentemente per Stephanie. Una teoria plausibile, avanzata da Tony Rothman, è che lo sfidante fosse Ernest Duchâtelet, che era stato in prigione con Galois. Pare che il duello si sia svolto secondo la roulette russa, scegliendo a caso tra due pistole di cui una sola carica, e sparando a bruciapelo. Galois scelse la pistola sbagliata, fu colpito al ventre, e morì il giorno dopo.
La notte precedente al duello scrisse una lunga esposizione delle sue idee matematiche, descrivendo anche la sua dimostrazione dell’impossibilità di una soluzione per radicali di tutte le equazioni di grado 5 o superiore. In questo lavoro Galois sviluppò il concetto di gruppo di permutazioni, e ottenne i primi risultati significativi per la teoria dei gruppi. Il suo manoscritto rischiò di andare perduto, ma riuscì ad arrivare nelle mani di Joseph Liouville, un membro dell’Académie. Nel 1843 Liouville parlò all’Académie, riferendo che nei manoscritti di Galois aveva trovato una soluzione «tanto corretta quanto è profondo questo piacevole problema: data un’equazione irriducibile di primo grado, decidere se è risolvibile per radicali oppure no». Liouville pubblicò il lavoro di Galois nel 1846, rendendolo finalmente accessibile alla comunità matematica.
Jordan
Il concetto di gruppo fu introdotto esplicitamente per la prima volta nel lavoro di Galois, anche se alcuni primi accenni si trovano nell’opera epica di Ruffini e nelle eleganti ricerche di Lagrange. Nell’arco di un decennio dalla diffusione delle idee di Galois, per opera di Liouville, la matematica poté contare su una teoria dei gruppi ben formata. L’artefice principale di questa teoria fu Camille Jordan, la cui opera in 667 pagine, Traité de substitutions et des équations algébrique, fu pubblicata nel 1870. Jordan sviluppò tutto l’argomento in una maniera sistematica ed esauriente.
L’interesse di Jordan per la teoria dei gruppi aveva avuto inizio nel 1867, al tempo in cui ne aveva mostrato in maniera esplicita il profondo collegamento con la geometria, classificando i tipi fondamentali di movimento di un corpo rigido nello spazio euclideo. Un contributo ancora più importante venne dal suo ottimo tentativo di classificare la maniera di combinare questi movimenti in gruppi. Lo stimolo principale gli veniva dal lavoro di Auguste Bravais, che aveva intrapreso uno studio matematico delle simmetrie cristalline, e in particolare del reticolo atomico sottostante. Gli articoli di Jordan generalizzavano le ricerche di Bravais: egli annunciò la sua classificazione nel 1867, e ne pubblicò i particolari negli anni 1868-1869.
Dal punto di vista tecnico, Jordan trattava
soltanto gruppi chiusi, in cui il limite di qualunque
successione di movimenti nel gruppo è anche un movimento nello
stesso gruppo. Questi comprendono tutti i gruppi finiti, per
ragioni banali, e anche gruppi come tutte le rotazioni di una
circonferenza attorno al suo centro. Un tipico esempio di gruppo
non chiuso, che non fu preso in considerazione da Jordan, potrebbe
essere quello di tutte le rotazioni di una circonferenza attorno al
suo centro per multipli razionali di 360°. Questo gruppo esiste, ma
non soddisfa la proprietà del limite (perché, per esempio, non
include la rotazione per  gradi, dal momento che
gradi, dal momento che
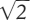 non è razionale). I gruppi di
movimenti non chiusi sono incredibilmente vari e quasi certamente
vanno oltre ogni classificazione ragionevole. Quelli chiusi sono
trattabili, ma difficili.
non è razionale). I gruppi di
movimenti non chiusi sono incredibilmente vari e quasi certamente
vanno oltre ogni classificazione ragionevole. Quelli chiusi sono
trattabili, ma difficili.
Quello che la teoria dei gruppi fece per loro
Una delle prime importanti applicazioni della teoria dei gruppi alla scienza fu la classificazione di tutte le possibili strutture cristalline. Gli atomi in un cristallo formano un reticolo tridimensionale regolare, e la difficoltà matematica fondamentale consiste nell’elencare tutti i possibili gruppi di simmetria di tali reticoli, perché questi di fatto formano le simmetrie del cristallo.
Nel 1891 Evgraf Fedorov e Arthur Schönflies dimostrarono che esistevano esattamente 230 gruppi spaziali cristallografici distinti. William Barlow ottenne un elenco simile ma incompleto.
Alcune tecniche moderne per trovare la struttura di molecole biologiche, come le proteine, si basano sul passaggio di raggi X attraverso un cristallo formato da quella molecola e sull’osservazione del modello di diffrazione risultante. Le simmetrie del cristallo sono importanti per dedurre la forma della molecola in esame. Lo stesso fa l’analisi di Fourier.
I principali movimenti rigidi nel piano sono le traslazioni, le rotazioni, le riflessioni e le glissoriflessioni (riflessioni con scorrimento). Nello spazio tridimensionale, incontriamo anche il movimento a vite, come quello di un cavatappi: l’oggetto trasla lungo un asse fissato e simultaneamente ruota attorno allo stesso.
Jordan iniziò con i gruppi di traslazioni, e ne elencò dieci tipi, tutti combinazioni di traslazioni continue (di una distanza a piacere) in certe direzioni e traslazioni discrete (per multipli interi di una distanza fissata) in direzioni diverse. Elencò anche i principali gruppi finiti di rotazioni e riflessioni: ciclico, diedrale, tetraedrale, ottaedrale, e icosaedrale. Distinse il gruppo O(2) di tutte le rotazioni e riflessioni che lasciano fissa nello spazio una retta, l’asse, e il gruppo O(3) di tutte le rotazioni e riflessioni che lasciano fisso nello spazio un punto, il centro.
In seguito divenne chiaro che il suo elenco era incompleto. Per esempio, Jordan non aveva considerato alcuni dei più particolari gruppi cristallografici nello spazio tridimensionale. Il suo lavoro rappresentò comunque un importante progresso verso la comprensione dei movimenti rigidi euclidei, che sono importanti in meccanica, come anche nel corpus principale della matematica pura.
Il libro di Jordan è davvero di vasta portata. Parte dall’aritmetica modulare e i campi di Galois, i quali oltre a fornire esempi di gruppi rappresentano anche il requisito fondamentale per ogni altro argomento contenuto nell’opera. La parte centrale tratta i gruppi di permutazioni, che Jordan chiama sostituzioni. Espone i concetti fondamentali dei sottogruppi normali, cioè quelli usati da Galois per dimostrare che il gruppo di simmetria dell’equazione di quinto grado è incoerente con una soluzione per radicali, e dimostra che questi sottogruppi possono essere usati per scomporre un gruppo generale in parti più semplici. Dimostra che le dimensioni di queste parti non dipendono dal modo in cui è scomposto il gruppo originario. Nel 1889 Otto Hölder migliorò questo risultato, interpretando le parti come gruppi a sé, e dimostrò che la loro struttura di gruppo, non soltanto la loro dimensione, è indipendente dal modo in cui è scomposto il gruppo. Oggi questo risultato è noto come teorema di Jordan-Hölder.
Un gruppo è semplice se non si scompone
in questo modo. Il teorema di Jordan-Hölder di fatto ci dice che i
gruppi semplici hanno con i gruppi generali la stessa relazione che
gli atomi hanno con le molecole in chimica. I gruppi semplici sono
i costituenti atomici di tutti i gruppi. Jordan dimostrò che il
gruppo alternante An, che comprende tutte le
permutazioni di n simboli che cambiano un numero pari di
coppie di simboli, è semplice per  Questa è la principale
motivazione della teoria di gruppi per cui l’equazione di quinto
grado non è risolvibile per radicali.
Questa è la principale
motivazione della teoria di gruppi per cui l’equazione di quinto
grado non è risolvibile per radicali.
Un nuovo sviluppo importante venne dalla teoria di Jordan delle sostituzioni lineari. In questo caso le trasformazioni che compongono il gruppo non sono permutazioni di un insieme finito, ma variazioni lineari di un elenco finito di variabili. Per esempio, tre variabili x, y, z potrebbero trasformarsi in nuove variabili X, Y, Z per mezzo delle equazioni lineari
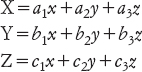
dove tutte le a, le b e le c sono costanti. Per rendere finito il gruppo, Jordan in genere considerava queste costanti come elementi degli interi modulo qualche numero primo, o più in generale di un campo di Galois.
Sempre nel 1869, Jordan sviluppò la propria versione della teoria di Galois e la incluse nel Traité. Dimostrò che un’equazione è risolvibile se e soltanto se il suo gruppo è risolvibile, cioè se le componenti semplici hanno tutte ordine primo. Applicò la teoria di Galois ai problemi geometrici.
Simmetria
I tentativi, in corso da quattromila anni, di risolvere le equazioni algebriche di quinto grado subirono una brusca interruzione quando Ruffini, Abel e Galois dimostrarono l’impossibilità di ottenere una soluzione per radicali. Anche se si trattava di un risultato negativo, ebbe comunque una vasta influenza sui successivi sviluppi sia della matematica che della scienza. Questo accadde perché il metodo introdotto per dimostrare l’impossibilità si rivelò cruciale nella comprensione matematica della simmetria, e la simmetria si rivelò vitale tanto nella matematica quanto nella scienza.
Gli effetti furono profondi. La teoria dei gruppi condusse a una visione più astratta dell’algebra, e con essa a una visione più astratta della matematica. Anche se molti scienziati pragmatici in principio si opposero a uno spostamento verso l’astrazione, alla fine fu chiaro che i metodi astratti sono spesso più potenti di quelli concreti, e le resistenze per lo più scomparvero. La teoria dei gruppi rese anche chiaro che i risultati negativi possono comunque essere importanti, e che insistere su una dimostrazione può talvolta condurre a notevoli scoperte. Supponiamo che i matematici avessero semplicemente ipotizzato senza dimostrarlo che le equazioni di quinto grado fossero insolubili, basandosi ragionevolmente sul fatto che nessuno potesse trovare una soluzione. Allora nessuno avrebbe inventato la teoria dei gruppi per spiegare perché quelle equazioni erano insolubili. Se i matematici avessero intrapreso la via facile, e avessero semplicemente riconosciuto che la soluzione era impossibile, la matematica e la scienza non sarebbero che il pallido riflesso di quello che sono oggi.
Ecco perché i matematici insistono sulle dimostrazioni.
Quello che la teoria dei gruppi fa per noi
La teoria dei gruppi è ora indispensabile in tutta la matematica, e il suo uso nella scienza è diffuso. In particolare, si presenta nelle teorie sulla formazione di modelli regolari in molti contesti scientifici differenti.
Un esempio è dato dalla teoria delle equazioni di reazione-diffusione, introdotta da Alan Turing nel 1952 come possibile spiegazione di disegni simmetrici nel mantello di alcuni animali. In queste equazioni, un sistema di sostanze chimiche può diffondersi in una regione di spazio, e le sostanze possono anche reagire per produrre nuovi elementi. Turing suggerì che alcuni di questi processi potessero innescare un disegno primitivo nell’embrione in formazione, per trasformarsi in seguito in pigmento, fino a rivelare il disegno nell’adulto.
Supponiamo per semplicità che la regione sia un piano. Allora le equazioni sono simmetriche per tutti i movimenti rigidi. L’unica soluzione delle equazioni che sia simmetrica per tutti i movimenti rigidi è uno stato uniforme, lo stesso in ogni punto. Questo si tradurrebbe in un animale senza alcun disegno specifico, di colore uniforme. Ad ogni modo, lo stato uniforme può essere instabile, e in questo caso la soluzione reale osservata sarà simmetrica per alcuni movimenti rigidi ma non per altri. Questo processo è detto rottura di simmetria.
Un tipico modello di rottura di simmetria nel piano vede la formazione di strisce parallele. Un altro è rappresentato da una livrea a macchie regolari. Sono anche possibili disegni più complicati. È interessante notare che macchie e strisce sono tra i disegni più comuni nel mantello degli animali, e molti dei disegni matematici più complicati si ritrovano pure negli animali. I reali processi biologici, che coinvolgono effetti genetici, devono essere più complicati di quanto ipotizzato da Turing, ma i meccanismi sottostanti di rottura di simmetria devono essere molti simili in termini matematici.