14.

L’algebra diventa maggiorenne

I numeri cedono il passo alle strutture

Nel 1860 la teoria dei gruppi di permutazione era ormai ampiamente sviluppata. La teoria degli invarianti – espressioni algebriche che non cambiano quando si operano alcuni cambiamenti di variabile – aveva attirato l’attenzione su diversi insiemi infiniti di trasformazioni, come il gruppo proiettivo di tutte le proiezioni dello spazio. Nel 1868 Camille Jordan aveva studiato i gruppi di movimenti nello spazio a tre dimensioni, e i due filoni avevano iniziato a convergere.

Concetti sofisticati

Cominciò a imporsi un nuovo tipo di algebra, nella quale gli oggetti di studio non erano numeri incogniti, ma concetti più sofisticati: permutazioni, trasformazioni, matrici. Quelli che erano procedimenti erano ora diventati oggetti reali. Le regole dell’algebra, ormai accettate, richiesero diverse modifiche che le rendessero adatte alle necessità di queste nuove strutture. Insieme ai gruppi, i matematici iniziarono a studiare strutture chiamate anelli e campi, e una varietà di algebre.

Una spinta a questa diversa concezione delle algebre venne dalle equazioni differenziali parziali, dalla meccanica e dalla geometria: lo sviluppo dei gruppi di Lie e delle algebre di Lie. Un’altra fonte di ispirazione fu la teoria dei numeri: qui i numeri algebrici potevano essere usati per risolvere le equazioni diofantee, comprendere le leggi di reciprocità e persino affrontare l’ultimo teorema di Fermat. Di fatto, il culmine di questi sforzi fu la dimostrazione dell’ultimo teorema di Fermat da parte di Andrew Wiles nel 1995.

Lie e Klein

Nel 1869 il matematico norvegese Sophus Lie divenne amico del matematico prussiano Felix Klein. Coltivavano un interesse comune per la geometria delle linee, un ramo collaterale della geometria proiettiva introdotto da Julius Plücker. Lie concepì un’idea molto originale, cioè che la teoria di Galois delle equazioni algebriche avesse un analogo per le equazioni differenziali. Un’equazione algebrica può essere risolta per radicali soltanto se ha il giusto tipo di simmetrie, cioè se ha un gruppo di Galois risolvibile. In maniera analoga, Lie suppose che un’equazione differenziale potesse essere risolta con metodi classici soltanto quando rimaneva invariata rispetto a una famiglia di trasformazioni continue. Lie e Klein lavorarono sulle variazioni di questa idea tra il 1869 e il 1870; l’apice si ebbe nel 1872 con la caratterizzazione da parte di Klein della geometria come gli invarianti di un gruppo, esposta nel suo programma di Erlangen.

Questo programma ebbe origine da un nuovo modo di pensare alla geometria euclidea, in termini delle sue simmetrie. Jordan aveva già sottolineato che le simmetrie del piano euclideo sono movimenti rigidi di vario tipo: traslazioni, che spostano il piano in una qualche direzione; rotazioni, che lo ruotano attorno ad alcuni punti fissi; riflessioni, che lo spostano al di là di una certa linea fissata; e, in maniera meno ovvia, le glissoriflessioni, che lo riflettono e poi lo traslano nella direzione perpendicolare alla linea dello specchio. Queste trasformazioni formano un gruppo, il gruppo euclideo, e sono rigide nel senso che non modificano le distanze, e quindi non cambiano neppure gli angoli. Lunghezze e angoli sono, come sappiamo, i concetti fondamentali della geometria euclidea. Klein comprese quindi che questi concetti sono gli invarianti del gruppo euclideo, le quantità che non cambiano quando si applica una trasformazione che fa parte del gruppo.

Se conosciamo il gruppo euclideo, possiamo infatti dedurre i suoi invarianti, e da questi ottenere la geometria euclidea.

Lo stesso accade per altri tipi di geometria. La geometria ellittica è lo studio degli invarianti del gruppo di movimenti rigidi in uno spazio a curvatura positiva, la geometria iperbolica è lo studio degli invarianti del gruppo di movimenti rigidi in uno spazio a curvatura negativa, la geometria proiettiva è lo studio degli invarianti del gruppo di proiezioni e via dicendo. Come le coordinate stabiliscono una relazione tra l’algebra e la geometria, così gli invarianti collegano la teoria dei gruppi alla geometria. Ogni geometria definisce un gruppo corrispondente, il gruppo di tutte le trasformazioni che preservano i concetti geometrici rilevanti. Al contrario, ogni gruppo di trasformazioni definisce una geometria corrispondente, quella degli invarianti.

Klein utilizzò questa corrispondenza per dimostrare che alcune geometrie erano in gran parte simili ad altre, poiché i loro gruppi erano identici tranne che per l’interpretazione. Il messaggio più profondo è che ogni geometria è definita dalle sue simmetrie. Esiste un’eccezione: la geometria delle superfici di Riemann, la cui curvatura può cambiare da punto a punto. Non si adatta affatto al programma di Klein.

I gruppi di Lie

La ricerca congiunta di Lie e Klein portò Lie a introdurre una delle idee più importanti della matematica moderna, cioè quella di un gruppo di trasformazione continuo, ora conosciuto come gruppo di Lie. Si tratta di un concetto che ha rivoluzionato tanto la matematica quanto la fisica, poiché i gruppi di Lie comprendono molte delle simmetrie più significative dell’universo fisico, e la simmetria è un potente principio organizzatore – sia per la filosofia sottostante alla maniera in cui noi rappresentiamo la natura in termini matematici, che per i calcoli tecnici.

Sophus Lie mise a punto la teoria dei gruppi in un impeto di creatività, a partire dall’autunno del 1873. Il concetto di gruppo di Lie si era considerevolmente evoluto a partire dai primi lavori di Lie. In termini moderni, un gruppo di Lie è una struttura che ha proprietà sia algebriche sia topologiche, che sono tra loro correlate. Nello specifico, è un gruppo (un insieme con un’operazione di composizione che soddisfa varie identità algebriche e soprattutto, com’è noto, la legge associativa) e una varietà topologica (uno spazio che localmente assomiglia allo spazio euclideo di dimensioni fissate, ma che può essere curvato o distorto in altro modo nel suo complesso), tale che la legge di composizione è continua (piccole variazioni negli elementi di partenza producono piccole variazioni nel risultato). Il concetto di Lie era più concreto: un gruppo di trasformazioni continue in molte variabili. Egli era approdato allo studio di questi gruppi di trasformazioni mentre cercava una teoria della risolvibilità o insolubilità delle equazioni differenziali, analoga a quella di Évariste Galois per le equazioni algebriche, ma oggi essi ricorrono in un’enorme varietà di contesti matematici, e la motivazione originale di Lie non è l’applicazione più importante.

Forse l’esempio più semplice di gruppo di Lie è dato dall’insieme di tutte le rotazioni di una circonferenza. Ogni rotazione è determinata unicamente da un angolo compreso tra 0° e 360°. L’insieme è un gruppo perché la composizione di due rotazioni è una rotazione, identificata dalla somma degli angoli corrispondenti. Si tratta di una varietà di dimensione uno, poiché gli angoli hanno una corrispondenza univoca con i punti su una circonferenza, e piccoli archi di circonferenza sono segmenti lineari leggermente curvi, essendo una linea uno spazio euclideo di dimensione uno. Infine, la legge di composizione è continua perché piccole variazioni degli angoli producono piccole variazioni nella loro somma.

Un esempio più stimolante è dato dal gruppo di tutte le rotazioni dello spazio tridimensionale che preservano una data origine. Ogni rotazione è determinata da un asse – una retta che passa per l’origine in una direzione arbitraria – e un angolo di rotazione attorno a questo asse. Sono necessarie due variabili per determinare un asse (per esempio la latitudine e la longitudine del punto in cui esso interseca una sfera di riferimento centrata nell’origine) e una terza per determinare l’angolo di rotazione; questo gruppo ha quindi dimensione tre. A differenza del gruppo di rotazioni di una circonferenza, questo non è commutativo: il risultato della combinazione di due trasformazioni dipende dall’ordine nel quale esse sono effettuate.

Nel 1873, dopo una parentesi dedicata alle equazioni differenziali parziali, Lie tornò a occuparsi dei gruppi di trasformazioni, studiando le proprietà delle trasformazioni infinitesimali. Dimostrò che le trasformazioni infinitesimali derivate da un gruppo continuo non sono chiuse per composizione, ma sono chiuse per una nuova operazione nota come parentesi, scritta [x, y]. Nella notazione delle matrici si tratta del commutatore xy − yx di x e y. La struttura algebrica risultante è ora conosciuta come algebra di Lie. Fino al 1930 circa le espressioni «gruppo di Lie» e «algebra di Lie» non erano usate: si faceva riferimento a questi concetti come a «gruppo continuo» e «gruppo infinitesimale» rispettivamente.

Esistono forti interconnessioni tra la struttura di un gruppo di Lie e quella della sua algebra di Lie, che Lie spiegò diffusamente in un’opera in tre volumi dal titolo Theorie der Trasformationsgruppen scritta insieme a Friedrich Engel. I due discussero dettagliatamente quattro famiglie di gruppi classiche, due delle quali sono i gruppi di rotazioni in uno spazio a n-dimensioni per n pari o dispari. I due casi sono piuttosto diversi, ed è per questo che sono importanti. Per esempio, nelle dimensioni dispari una rotazione possiede sempre un asse fisso; nelle dimensioni pari questo non accade.

Killing

Uno sviluppo successivo davvero importante venne da Wilhelm Killing. Nel 1888 Killing gettò le fondamenta di una teoria della struttura per le algebre di Lie, e in particolare classificò tutte le algebre di Lie semplici, i mattoni fondamentali che compongono tutte le altre algebre di Lie. Killing partì dalla struttura conosciuta delle algebre di Lie semplici più banali, le algebre di Lie lineari speciali sl(n), per Prendiamo tutte le matrici n × n con entrate complesse, e poniamo che la parentesi di Lie di due matrici A e B sia AB − BA. Questa algebra di Lie non è semplice, ma la sottoalgebra, sl(n), di tutte le matrici i cui termini diagonali danno come somma zero, è semplice. Ha dimensione n² − 1.

Killing conosceva la struttura di questa algebra, e dimostrò che qualunque algebra semplice di Lie possedeva un tipo di struttura simile. È notevole che egli riuscisse a dimostrare qualcosa di così specifico, sapendo soltanto che l’algebra di Lie è semplice. Il suo metodo consisteva nell’associare a ogni algebra di Lie semplice una struttura geometrica nota come sistema di radici. Egli utilizzava i metodi dell’algebra lineare per studiare e classificare i sistemi di radici, e poi derivava la struttura dell’algebra di Lie corrispondente da quella del sistema di radici. Una classificazione delle possibili geometrie del sistema di radici equivale di fatto a una classificazione delle algebre di Lie semplici.

Il risultato del lavoro di Killing è notevole. Egli dimostrò che le algebre di Lie semplici sono comprese in quattro famiglie infinite, ora chiamate A_n, B_n, C_n e D_n. Esistono inoltre cinque eccezioni: G₂, F₄, E₆, E₇ ed E₈. Killing in realtà pensava che esistessero sei eccezioni, ma due di queste si rivelarono la stessa algebra in due forme diverse. Le dimensioni delle algebre di Lie eccezionali sono 12, 56, 78, 133 e 248. Queste rimangono un poco misteriose, anche se ora noi comprendiamo piuttosto chiaramente il perché della loro esistenza.

I gruppi di Lie semplici

A causa delle strette connessioni tra un gruppo di Lie e la sua algebra di Lie, la classificazione delle algebre di Lie semplici conduce anche a una classificazione dei gruppi di Lie semplici. In particolare le quattro famiglie A_n, B_n, C_n e D_n sono le algebre di Lie delle quattro famiglie classiche dei gruppi di trasformazioni. Queste sono, rispettivamente, il gruppo di tutte le trasformazioni lineari in uno spazio (n + 1)-dimensionale, il gruppo di rotazioni in uno spazio (2n + 1)-dimensionale, il gruppo simplettico in 2n dimensioni, che è importante in meccanica classica e quantistica e in ottica, e il gruppo di rotazioni nello spazio 2n-dimensionale. Qualche tocco finale a questa storia fu aggiunto in seguito; degna di nota è l’introduzione fatta da Harold Scott MacDonald Coxeter ed Eugene (Evgenii) Dynkin di un metodo grafico per l’analisi combinatoria dei sistemi di radici, ora conosciuto con il nome di diagramma di Coxeter o di Dynkin.

I gruppi di Lie sono importanti nella matematica moderna per molte ragioni. In meccanica, per esempio, molti sistemi presentano simmetrie, e quelle simmetrie rendono possibile trovare soluzioni alle equazioni dinamiche. Le simmetrie formano generalmente un gruppo di Lie. In fisica matematica, lo studio delle particelle elementari si basa fortemente sul sistema dei gruppi di Lie, sempre per certi principi di simmetria. Il gruppo eccezionale di Killing E₈ riveste un ruolo notevole nella teoria delle superstringhe, un importante approccio moderno all’unificazione tra meccanica quantistica e relatività generale. La fondamentale scoperta, effettuata nel 1983 da Simon Donaldson, che lo spazio euclideo a quattro dimensioni ha strutture differenziabili non tradizionali poggia, in sostanza, su una caratteristica inconsueta del gruppo di Lie di tutte le rotazioni in uno spazio a quattro dimensioni. La teoria dei gruppi di Lie è vitale per tutta la matematica moderna.

Gruppi astratti

Nel programma di Erlangen di Klein è essenziale che i gruppi coinvolti contengano trasformazioni: vale a dire che gli elementi del gruppo agiscano su uno spazio. Gran parte dei primi lavori sui gruppi presume questa struttura. Ricerche successive richiesero però un’ulteriore astrazione: conservare le proprietà di gruppo ma eliminare lo spazio. Un gruppo era composto di entità matematiche che potevano essere combinate per formare entità simili, ma quelle entità non dovevano essere trasformazioni.

I numeri sono un esempio. Due numeri (interi, razionali, reali, complessi) possono essere sommati, e il risultato è un numero dello stesso tipo. I numeri formano un gruppo per l’operazione di addizione. I numeri però non sono trasformazioni. Quindi, anche se considerare i gruppi come trasformazioni aveva unificato la geometria, l’ipotesi di uno spazio sottostante doveva essere eliminata per unificare la teoria dei gruppi.

Uno dei primi ad avvicinarsi a questo passo fu Arthur Cayley, in tre articoli del 1849 e del 1854. Qui Cayley affermava che un gruppo comprende un insieme di operatori 1, a, b, c e così via. La combinazione ab di due operatori qualunque deve essere un altro operatore; l’operatore speciale 1 soddisfa 1a = a e a1 = a per tutti gli operatori a; infine, deve valere la legge associativa (ab)c = a(bc). Questi operatori però agiscono ancora su qualcosa (un insieme di variabili). Cayley aveva inoltre trascurato una proprietà fondamentale: ogni a deve avere un inverso a′ tale che a′a = aa′ = 1. Cayley era quindi arrivato vicino alla soluzione, ma aveva perso il premio per un pelo.

Nel 1858 Richard Dedekind consentì agli elementi del gruppo di essere entità arbitrarie, non soltanto trasformazioni oppure operatori, ma incluse la legge commutativa ab = ba nella sua definizione. La sua idea era giusta per il suo obiettivo dichiarato, la teoria dei numeri, ma escludeva la maggior parte dei gruppi interessanti nella teoria di Galois, per non parlare del mondo matematico più vasto. Il concetto moderno di gruppo astratto fu introdotto nel 1882-83 da Walther Van Dyck. Questi introdusse l’esistenza di un inverso, ma negò la necessità di una legge commutativa. Un trattamento assiomatico dei gruppi a tutto campo venne qualche tempo dopo, per opera di Edward Huntington ed Eliakim Moore nel 1902, e di Leonard Dickson nel 1905.

Con la struttura astratta dei gruppi separata ora da qualsiasi specifica interpretazione, l’argomento si sviluppò rapidamente. La prima fase della ricerca consisteva soprattutto nel «collezionare farfalle»: si studiavano i singoli esempi di gruppi, oppure tipi speciali, alla ricerca di caratteristiche comuni. I principali concetti e metodi apparvero abbastanza presto, e le ricerche fiorirono.

La teoria dei numeri

Un’altra importante fonte di nuovi concetti algebrici fu la teoria dei numeri. Gauss aveva dato avvio al processo quando aveva introdotto quelli che ora chiamiamo interi gaussiani: numeri complessi a + bi, con a e b interi. Le somme e i prodotti di tali numeri hanno la stessa forma. Gauss scoprì che il concetto di numero primo si generalizza agli interi gaussiani. Un intero gaussiano è primo se non può essere espresso come prodotto di altri interi gaussiani in una maniera non banale. La fattorizzazione in primi per gli interi gaussiani è unica. Alcuni numeri primi ordinari, come 3 e 7, sono primi anche quando sono considerati come interi gaussiani, ma altri invece no: per esempio 5 = (2 + i)(2 − i). Questo fatto ha una stretta relazione con il teorema di Fermat sui numeri primi e le somme di due quadrati, e gli interi gaussiani chiariscono quel teorema e i suoi simili.

Se dividiamo un intero gaussiano per un altro, il risultato può non essere un intero gaussiano, ma gli si avvicina: è della forma a + bi, con a e b razionali. Questi sono i numeri gaussiani. Più in generale, gli studiosi di teoria dei numeri hanno scoperto che qualcosa di simile accade se consideriamo un polinomio p(x) con coefficienti interi, e poi consideriamo tutte le combinazioni lineari a₁x₁+ …. + a_nx_n delle sue soluzioni x₁, …, x_n. Considerando a₁, …, a_n razionali, otteniamo un sistema di numeri complessi che è chiuso per addizione, sottrazione, moltiplicazione e divisione (definizione con la quale si intende che applicando queste operazioni a un numero di questo tipo, il risultato è un numero dello stesso tipo). Questo sistema costituisce un campo numerico algebrico. Se invece si richiede che a₁, …, a_n siano interi, il sistema è chiuso per addizione, sottrazione e moltiplicazione, ma non per divisione: si tratta di un anello numerico algebrico.

L’applicazione più grandiosa di questi nuovi sistemi numerici si ebbe con l’ultimo teorema di Fermat: l’affermazione che l’equazione di Fermat, xⁿ + yⁿ = zⁿ, non ha alcuna soluzione intera se la potenza n è uguale o maggiore di 3. Nessuno era in grado di ricostruire la presunta «notevole dimostrazione» e sembrava sempre meno probabile che lo stesso Fermat ne avesse una. Ad ogni modo, qualche risultato si ottenne. Fermat aveva trovato una dimostrazione per i cubi e le potenze di quarto grado, Peter Lejeune-Dirichlet si era occupato delle potenze di quinto grado nel 1828 e Henri Lebesgue aveva trovato una dimostrazione per le potenze di settimo grado nel 1840.

Nel 1847, Gabriel Lamé enunciò una dimostrazione per le potenze di ogni grado, ma Ernst Eduard Kummer individuò un errore. Lamé aveva supposto senza dimostrarlo che l’unicità della fattorizzazione in primi è valida per i numeri algebrici, ma questo è falso per alcuni campi numerici algebrici, anzi per la maggior parte di essi. Kummer dimostrò che l’unicità non vale per il campo numerico algebrico che nasce dallo studio dell’ultimo teorema di Fermat per le potenze di ordine 23. Kummer però non si diede per vinto, e trovò la maniera di aggirare l’ostacolo escogitando alcuni nuovi marchingegni matematici, e sviluppando la teoria dei numeri ideali. Nel 1847 aveva definito l’ultimo teorema di Fermat per tutte le potenze fino a 100, tranne che per 37, 59 e 67. Sviluppando ulteriori stratagemmi, nel 1857 Kummer e Dimitri Mirimanoff risolsero anche questi casi. Negli anni ottanta del Novecento erano ormai stati dimostrati con metodi simili tutti i casi fino alla potenza 150 000, ma il metodo poteva dichiararsi esaurito.

Anelli, campi e algebre

Il concetto di Kummer di numero ideale era ingombrante, e Dedekind lo riformulò in termini di ideali, sottosistemi particolari di interi algebrici. Con l’apporto della scuola di Hilbert a Göttingen, e in particolare grazie a Emmy Noether, l’argomento fu dotato di un fondamento assiomatico. A fianco dei gruppi, furono definiti tre tipi diversi di sistemi algebrici, per mezzo di opportuni elenchi di assiomi: anelli, campi e algebre.

In un anello, le operazioni di addizione, sottrazione e moltiplicazione sono definite, e soddisfano tutte le tradizionali leggi dell’algebra tranne la legge commutativa della moltiplicazione. Se anche questa legge vale, si ha un anello commutativo.

In un campo, le operazioni di addizione, sottrazione, moltiplicazione e divisione sono definite, e soddisfano tutte le tradizionali leggi dell’algebra, compresa la legge commutativa della moltiplicazione. Se questa legge non vale, si ha un anello di divisione.

Un’algebra è come un anello, ma i suoi elementi possono anche essere moltiplicati per diverse costanti, i numeri reali, i numeri complessi oppure – nel caso più generale – per un campo. Le leggi di addizione sono quelle solite, ma la moltiplicazione può soddisfare una varietà di assiomi differenti. Se è associativa, si ha un’algebra associativa. Se soddisfa alcune regole collegate al commutatore xy − yx, è un’algebra di Lie.

Esistono dozzine, forse centinaia di specie differenti di strutture algebriche, ciascuna con la propria lista di assiomi. Alcune sono state inventate soltanto per esplorare le conseguenze di assiomi interessanti, ma la maggior parte di esse nasce da una necessità in qualche problema specifico.

Gruppi semplici finiti

Il punto più alto della ricerca del XX secolo sui gruppi finiti fu la felice classificazione di tutti i gruppi semplici finiti. Questo definì per i gruppi finiti quanto Killing aveva ottenuto per i gruppi di Lie e le loro algebre di Lie. Si arrivò infatti a una completa descrizione di tutti i possibili elementi costitutivi dei gruppi finiti, i gruppi semplici. Se i gruppi sono molecole, i gruppi semplici sono i loro atomi costituenti.

La classificazione di Killing dei gruppi semplici di Lie dimostrò che questi devono appartenere a una delle quattro famiglie infinite A_n, B_n, C_n e D_n, con esattamente cinque eccezioni, G₂, F₄, E₆, E₇ ed E₈. La classificazione finale di tutti i gruppi semplici finiti fu ottenuta da molti matematici, così tanti che è impossibile ricordarli tutti in questa sede, ma il programma complessivo per risolvere questo problema si deve a Daniel Gorenstein. La risposta, pubblicata nel 1888-90, è stranamente simile: un elenco di famiglie infinite, e un elenco di eccezioni. Ora però le famiglie sono molte di più, e le eccezioni arrivano a 26.

Le famiglie comprendono i gruppi alternanti (già noti a Galois) e una grande quantità di gruppi del tipo di Lie che sono come i gruppi di Lie semplici ma su diversi campi finiti piuttosto che su numeri complessi. Esistono anche alcune curiose varianti di questo tema. Le eccezioni sono 26 diverse, con alcuni aspetti in comune, ma nessuna struttura unificata. La prima dimostrazione della completezza della classificazione si ebbe grazie al lavoro congiunto di centinaia di matematici, ed era lunga complessivamente circa 10 000 pagine (senza contare il fatto che alcune parti fondamentali della dimostrazione non vennero pubblicate). Un lavoro recente a cura di quanti ancora si dedicano a questo argomento ha portato a una nuova classificazione più semplificata, con un approccio possibile grazie alla conoscenza preventiva delle risposte. I risultati sono in via di pubblicazione in una serie di volumi, per un totale di circa 2000 pagine.

Il più misterioso dei gruppi semplici eccezionali, e il più grande, è il gruppo mostro. Il suo ordine è

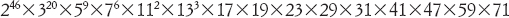
che equivale a

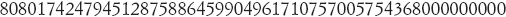
ed è all’incirca 8 × 10⁵³. La sua esistenza era stata ipotizzata nel 1973 da Bernd Fischer e Robert Griess. Nel 1980 Griess dimostrò che esisteva, e fornì una costruzione algebrica come il gruppo di simmetria di un’algebra a 196 884 dimensioni. Il mostro sembrava avere alcune inattese connessioni con la teoria dei numeri e l’analisi complessa, enunciate da John Conway come la congettura Monstrous Moonshine. Questa congettura fu dimostrata da Richard Borcherds nel 1992, il quale per questo fu insignito della Fields Medal, il riconoscimento più prestigioso in matematica.

L’ultimo teorema di Fermat

L’applicazione dei campi numerici algebrici alla teoria dei numeri si sviluppò rapidamente nella seconda metà del XX secolo, e stabilì contatti con molte altre branche della matematica, compresa la teoria di Galois e la topologia algebrica. Il punto più alto di questo lavoro fu una dimostrazione dell’ultimo teorema di Fermat, circa 350 anni dopo la sua prima formulazione.

L’idea davvero decisiva venne da quella bellissima area di ricerca che è al cuore dei moderni studi sulle equazioni diofantee: la teoria delle curve ellittiche. Si tratta di equazioni nelle quali un quadrato perfetto è uguale a un polinomio cubico, e rappresentano l’unico aspetto delle equazioni diofantee che i matematici comprendono davvero bene. Anche in questo settore, comunque, esistono importanti questioni irrisolte. La più importante di tutte è la congettura di Taniyama-Weil, che prende il nome da Yutaka Taniyama e André Weil. Questa afferma che ogni curva ellittica può essere rappresentata in termini di funzioni modulari, cioè generalizzazioni delle funzioni trigonometriche studiate in particolare da Klein.

All’inizio degli anni ottanta, Gerhard Frey trovò una relazione tra l’ultimo teorema di Fermat e le curve ellittiche. Supponiamo che esista una soluzione per l’equazione di Fermat; allora è possibile costruire una curva ellittica dalle proprietà molto particolari, così particolari che l’esistenza della curva sembra davvero improbabile. Nel 1986 Kenneth Ribet precisò meglio questa idea, dimostrando che se la congettura di Taniyama-Weil è vera, allora la curva di Frey non può esistere. Di conseguenza non può esistere nemmeno la presunta soluzione dell’equazione di Fermat, e questo dimostrerebbe l’ultimo teorema di Fermat. L’approccio dipendeva dalla congettura di Taniyama-Weil, ma dimostrava che l’ultimo teorema di Fermat non era soltanto una curiosità storica isolata, e anzi si collocava al cuore della moderna teoria dei numeri.

Andrew Wiles, da bambino, aveva sognato di dimostrare l’ultimo teorema di Fermat, ma quando divenne un matematico decise che si trattava soltanto di un problema isolato, irrisolto, ma non davvero importante. Il lavoro di Ribet gli fece cambiare idea. Nel 1993 annunciò una dimostrazione della congettura di TaniyamaWeil per una classe speciale di curve ellittiche, abbastanza generale da dimostrare l’ultimo teorema di Fermat. Quando però l’articolo fu presentato per la pubblicazione, si evidenziò una importante lacuna. Wiles aveva quasi gettato la spugna, quando «all’improvviso, in modo del tutto inaspettato, ebbi questa rivelazione incredibile […] era una soluzione così indescrivibilmente bella, era così semplice e così elegante, e la fissai incredulo». Con l’aiuto di Richard Taylor, rivide completamente la dimostrazione e corresse l’errore. Il suo articolo fu pubblicato nel 1995.

Possiamo essere certi che l’idea di Fermat, qualunque fosse al tempo in cui sosteneva di possedere una dimostrazione del suo ultimo teorema, era molto lontana dal metodo usato da Wiles.

Aveva davvero Fermat una dimostrazione semplice e meravigliosa, oppure si illudeva? È un mistero che, a differenza dell’ultimo teorema, non sarà mai risolto.

Matematica astratta

La deviazione verso una concezione più astratta della matematica venne come naturale conseguenza della varietà sempre più ampia dei suoi oggetti di studio. Quando la matematica riguardava soprattutto i numeri, i simboli algebrici erano semplicemente usati in sostituzione dei numeri. Con l’evoluzione della matematica però, i simboli iniziarono ad avere vita propria. Il significato dei simboli divenne meno importante rispetto alle regole che definivano la maniera di manipolarli. Nemmeno le regole erano considerate sacre: le leggi dell’aritmetica tradizionali, come la proprietà commutativa, non erano sempre appropriate nei nuovi contesti.

Non fu solo l’algebra a diventare astratta. Anche l’analisi e la geometria si focalizzarono su argomenti più generali, per ragioni simili. Il principale mutamento concettuale avvenne tra la metà del XIX secolo e la metà del XX secolo. In seguito, iniziò un periodo di consolidamento, mentre i matematici cercavano di trovare un equilibrio tra le contrastanti necessità di formalismo astratto e le applicazioni alla scienza. Astrazione e generalizzazione vanno di pari passo, ma l’astrazione può anche oscurare il significato della matematica. A questo punto però non è più importante stabilire se l’astrazione sia utile o necessaria: i metodi astratti hanno dimostrato la loro validità rendendo possibile la soluzione di numerosi problemi da tempo irrisolti, come l’ultimo teorema di Fermat. E quello che ieri sembrava poco più di un gioco formale può rivelarsi domani uno strumento scientifico o commerciale di importanza fondamentale.