7.
Modelli numerici
L’origine della teoria dei numeri
Anche se furono sempre più affascinati dalla geometria, i matematici non persero il loro interesse per i numeri. Cominciarono però a porsi interrogativi più profondi, e risposero a molti di questi. Altri dovettero aspettare lo sviluppo di tecniche più potenti, mentre alcuni rimangono irrisolti ancora oggi.
Teoria dei numeri
C’è qualcosa di affascinante nei numeri. Puri, sobri numeri interi, 1, 2, 3, 4, 5… Che cosa c’è di più semplice? Quell’apparenza semplice nasconde però profondità nascoste, e molti dei più sconcertanti interrogativi in matematica riguardano proprietà in apparenza banali dei numeri interi. Questa area è nota come teoria dei numeri, e si rivela difficile proprio perché i suoi ingredienti sono così elementari. La grande semplicità dei numeri interi lascia poco spazio alle tecniche ingegnose.
I primi seri contributi alla teoria dei numeri, completati cioè da dimostrazioni e non semplicemente enunciati, si trovano nelle opere di Euclide, dove le idee sono sottilmente contrabbandate come geometria. L’argomento fu sviluppato in un’area distinta della matematica dal greco Diofanto, del quale alcuni scritti sono giunti fino a noi come copie successive. La teoria dei numeri ebbe un grande impulso nel Seicento per opera di Fermat, e fu sviluppata da Leonhard Euler (Eulero), Giuseppe Luigi Lagrange e Carl Friedrich Gauss in un’estesa e profonda branca della matematica che coinvolse molte altre aree, spesso in apparenza separate. Alla fine del XX secolo questi collegamenti erano stati usati per rispondere ad alcuni (anche se non a tutti) antichi interrogativi, tra cui una famosissima congettura formulata da Fermat intorno al 1650, nota come il suo ultimo teorema.
Per la maggior parte della sua storia, la teoria dei numeri ha riguardato il funzionamento interno della matematica in sé, con poche connessioni con il mondo reale. Se è mai esistita una branca del pensiero matematico che ha vissuto nelle inebrianti altezze delle torri d’avorio, questa è stata la teoria dei numeri. L’arrivo dei computer elettronici, però, ha cambiato tutto questo. I computer lavorano con rappresentazioni elettroniche di numeri interi, e le questioni e le opportunità sollevate dai computer portano spesso alla teoria dei numeri. Dopo 2500 anni come puro esercizio intellettuale, la teoria dei numeri ha finalmente avuto un impatto sulla vita quotidiana.
Numeri primi
Chiunque pensi alla moltiplicazione dei numeri interi prima o poi nota una distinzione fondamentale.
Molti numeri possono essere scomposti in pezzi più piccoli, in quanto il numero in oggetto ha origine dalla moltiplicazione di quei pezzi. Per esempio, 10 è 2 × 5, e 12 è 3 × 4. Alcuni numeri, però, non si possono scomporre in questa maniera. Non c’è modo di esprimere 11 come il prodotto di due numeri interi più piccoli; lo stesso vale per 2, 3, 5, 7 e molti altri valori.
I numeri che possono essere espressi come il prodotto di due numeri più piccoli si dicono composti; quelli che non possono essere espressi in questo modo si dicono primi. In accordo con questa definizione, il numero 1 si dovrebbe considerare primo, ma per buone ragioni si considera come appartenente a una classe speciale ed è definito come una unità. I primi numeri primi sono

Come si capisce da questo elenco, non esiste un modello ovvio di distribuzione dei numeri primi (se si trascura il fatto che, tranne il primo, sono tutti dispari). In effetti, sembrano presentarsi con una certa irregolarità, e non esiste un modo semplice per prevedere il numero successivo nella lista. Eppure è fuori di dubbio che questo numero è in qualche modo determinato: basta esaminare i numeri successivi fino a trovare il prossimo primo.
Nonostante la loro distribuzione irregolare, o forse proprio per questo, i numeri primi sono di importanza cruciale in matematica. Rappresentano i mattoni fondamentali per tutti i numeri, nel senso che i numeri più grandi si formano moltiplicando numeri più piccoli. La chimica ci insegna che ogni molecola, per quanto complicata, è formata da atomi: particelle di materia indivisibili chimicamente. In maniera analoga, la matematica ci dice che ogni numero, per quanto grande possa essere, è costruito con primi: numeri indivisibili. I primi sono dunque gli atomi della teoria dei numeri.
Questa caratteristica dei numeri primi è utile perché molti problemi in matematica possono essere risolti per tutti i numeri interi, a patto di poter essere risolti per i primi, e i primi hanno proprietà speciali che talvolta rendono la soluzione del problema più semplice. Questo aspetto duale dei numeri primi (sono importanti ma sfuggono a un comportamento regolare) stimola la curiosità dei matematici.
Euclide
Euclide introdusse i numeri primi nel libro VII degli Elementi, e fornì le dimostrazioni di tre proprietà fondamentali. Nella terminologia moderna queste sono:
(i) ogni numero può essere espresso come un prodotto di primi;
(ii) questa espressione è unica tranne per l’ordine in cui compaiono i primi;
(iii) ci sono infiniti numeri primi.
Quello che Euclide realmente enunciò e dimostrò è leggermente diverso.
La proposizione 31 del libro VII afferma che ogni numero composto è misurato da qualche primo, vale a dire che può essere diviso esattamente da quel numero primo. Per esempio, 30 è un numero composto, ed è esattamente divisibile per diversi primi, tra cui 5: infatti 30 = 6 × 5. Iterando questo procedimento di estrazione di un divisore primo, o fattore, possiamo scomporre qualunque numero in un prodotto di primi. Dunque, partendo da 30 = 6 × 5, osserviamo che anche 6 è composto, e si ha 6 = 2 × 3. Ora, 30 = 2 × 3 × 5, e i tre fattori sono tutti numeri primi.
Perché l’unicità dei fattori primi non è ovvia
Poiché i primi sono gli atomi della teoria dei numeri, potrebbe sembrare ovvio che scomponendo un numero in primi si ottengano sempre gli stessi atomi. Dopo tutto, gli atomi sono le parti indivisibili. Se potessimo scomporre un numero in due maniere distinte, questo non vorrebbe dire scomporre un atomo? In questo caso però l’analogia con la chimica è leggermente fuorviante.
Per vedere che l’unicità della fattorizzazione in primi non è ovvia, possiamo operare con un insieme limitato di numeri:

e così via. L’elenco contiene i numeri che superano di una unità un multiplo di 4. I prodotti ottenuti moltiplicando tra loro questi numeri hanno la stessa proprietà, e allora possiamo formare tali numeri moltiplicando numeri più piccoli dello stesso tipo. Definiamo «quasi-primo» un numero che compare nell’elenco e che non è il prodotto di due numeri più piccoli che compaiono nell’elenco. Per esempio, 9 è quasi-primo: gli unici numeri più piccoli nell’elenco sono 1 e 5, e il loro prodotto non è 9. (È sempre vero che 9 = 3 × 3, naturalmente, ma il numero 3 non compare nell’elenco).
È ovvio – e vero – che ogni numero nell’elenco è un prodotto di quasi-primi. Ad ogni modo, anche se questi quasi-primi sono gli atomi dell’insieme, si verifica un fenomeno piuttosto strano. Il numero 693 si può scomporre in due maniere diverse: 693 = 9 × 77 = 21 × 33, e tutti e quattro i fattori, 9, 21, 33 e 77, sono quasi-primi. L’unicità della fattorizzazione fallisce dunque per questo tipo di numeri.
Se fossimo invece partiti da 30 = 10 × 3, allora avremmo scomposto il 10 come 10 = 2 × 5, per ottenere 30 = 2 × 5 × 3. Otteniamo gli stessi tre numeri primi, ma moltiplicati in un ordine differente, e questo naturalmente non modifica il risultato. Può sembrare ovvio che comunque scomponiamo un numero in primi, otteniamo sempre lo stesso risultato se non per l’ordine, ma questo può rivelarsi arduo da dimostrare. In effetti, simili enunciati in alcuni sistemi di numeri collegati si rivelano falsi, ma per i numeri interi ordinari l’affermazione è vera. La fattorizzazione in numeri primi è unica. Euclide dimostrò la proprietà fondamentale necessaria per stabilire l’unicità nella proposizione 30 del libro VII degli Elementi: se un primo divide il prodotto di due numeri, allora deve dividere almeno uno di quei numeri. Una volta che conosciamo la proposizione 30, l’unicità della fattorizzazione in numeri primi deriva come semplice conseguenza.
La proposizione 20 del libro IX suona così: «I numeri primi sono più di una qualsiasi assegnata moltitudine di numeri primi». Nella terminologia moderna, questo significa che la lista di numeri primi è infinita. La dimostrazione è fornita in un caso emblematico: supponiamo che ci siano soltanto tre numeri primi, a, b e c. Moltiplichiamoli insieme e aggiungiamo uno, per ottenere abc + 1. Questo numero deve essere divisibile per qualche numero primo, ma quel primo non può essere nessuno dei tre di partenza, dal momento che questi dividono abc esattamente, e dunque non possono dividere anche abc + 1, perché altrimenti dividerebbero la differenza, che è 1. Abbiamo perciò trovato un nuovo primo, e questo contraddice l’ipotesi che a, b e c siano gli unici numeri primi esistenti.
Il numero primo più grande conosciuto
Non esiste un numero primo più grande in assoluto, ma il primo più grande conosciuto a maggio del 2009 è 243.122.609 − 1, un numero con 12 978 189 cifre. Numeri della forma 2p − 1, con p numero primo, sono chiamati primi di Mersenne, perché nel 1644 Mersenne ipotizzò nel suo Cogitata physica-mathematica che questi numeri fossero primi per p = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127 e 257, e composti per tutti gli altri numeri interi minori di 257.
Esistono metodi particolari per verificare velocemente se questi numeri sono primi, e ora sappiamo che Mersenne commise cinque errori. I suoi numeri sono composti per p = 67 e 257, e ci sono tre primi aggiuntivi con p = 61, 89, 107. Ad oggi sono noti 44 primi di Mersenne. La scoperta di nuovi valori rappresenta un test efficace per i nuovi supercomputer, ma non ha alcuna utilità pratica.
Anche se la dimostrazione di Euclide usa tre numeri primi, la stessa idea funziona per un elenco più lungo. Si moltiplichino tutti i primi nell’elenco, si sommi uno e poi si prenda qualche fattore primo del risultato: questo genera sempre un primo che non è nella lista. Di conseguenza nessun elenco finito di numero primi può mai essere completo.
Diofanto
Abbiamo citato Diofanto di Alessandria a proposito della notazione algebrica, ma il più grande contributo da parte sua si ebbe nell’ambito della teoria dei numeri. Diofanto studiò questioni generali, piuttosto che particolari problemi numerici, anche se le sue risposte furono numeri specifici. Per esempio: «Si trovino tre numeri tali che la loro somma, e la somma di due qualsiasi di essi, sia un quadrato perfetto». La sua risposta è 41, 80 e 320. Prova: la somma di tutti e tre è 441 = 212. Le somme di coppie sono 41 + 80 = 112, 41 + 320 = 192 e 80 + 320 = 202.
Una delle equazioni più note risolte da Diofanto si presenta come una curiosa derivazione del teorema di Pitagora. Possiamo enunciare il teorema in termini algebrici: se un triangolo ha lati a, b, c dove c è il lato più lungo, allora a2 + b2 = c2. Esistono alcuni triangoli rettangoli particolari in cui i lati sono numeri interi. Il più semplice e il più noto si ha con a, b, c uguali a 3, 4 e 5 rispettivamente: in questo caso 32 + 42 = 9 + 16 = 25 = 52. Un altro esempio, il più semplice dopo il precedente, è 52 + 122 = 132.
In effetti, il numero di queste triplette pitagoriche è infinito. Diofanto trovò tutte le possibili soluzioni con numeri interi dell’equazione che noi ora scriviamo come a2 + b2 = c2. Il suo metodo prevede di prendere due numeri interi, e di calcolare la differenza tra i loro quadrati, il doppio del loro prodotto e la somma dei loro quadrati. Questi tre numeri formano sempre una tripletta pitagorica, e tutti i triangoli di questo tipo si trovano allo stesso modo, facendo sì che i tre numeri siano tutti moltiplicati per la stessa costante. Se i numeri sono 1 e 2, per esempio, otteniamo il famoso triangolo 3-4-5. In particolare, dal momento che esistono infiniti modi per scegliere i due numeri, esistono infinite triplette pitagoriche.
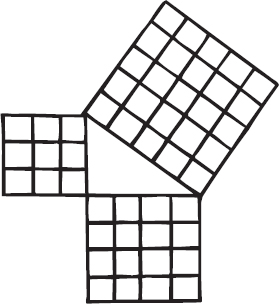
Figura 7.1
Il triangolo rettangolo 3-4-5.
Fermat
Dopo Diofanto, la teoria dei numeri subì una battuta di arresto per circa un millennio, fino a che fu ripresa da Fermat, che fece alcune importanti scoperte. Uno dei suoi teoremi più eleganti ci dice esattamente se un intero assegnato n è la somma di due quadrati perfetti: n = a2 + b2. La soluzione è più semplice se n è primo. Fermat osservò che esistono tre tipi fondamentali di primi:
(i) il numero 2, l’unico primo pari;
(ii) numeri primi che sono maggiori di 1 rispetto a un multiplo di 4, come 5, 13, 17 e così via – questi primi sono tutti dispari;
(iii) numeri primi che sono minori di 1 rispetto a un multiplo di 4, come 3, 7, 11 e così via – questi primi sono pure dispari.
Fermat dimostrò che un numero primo è la somma di due quadrati se appartiene alla classe (i) o (ii), e non è la somma di due quadrati se appartiene alla classe (iii).
Per esempio, 37 è nella categoria (ii), perché è 4 × 9 + 1, e 37 = 62 + 12, la somma di due quadrati. Viceversa, 31 = 4 × 8 − 1 è nella classe (iii), e se tentiamo tutte le possibili maniere di scrivere 31 come somma di due quadrati, non ne troveremo una valida. (Per esempio, 31 = 25 + 6, dove 25 è un quadrato, ma 6 no).
Quello che non sappiamo dei numeri primi
Anche oggi, i numeri primi continuano a riservare alcuni segreti. Due famosi problemi irrisolti sono la congettura di Goldbach e la congettura dei primi gemelli.
Christian Goldbach era un matematico dilettante che intratteneva una regolare corrispondenza con Eulero. In una lettera del 1742, Goldbach espose il risultato che ogni numero primo maggiore di 2 è la somma di tre primi. Egli considerava il numero 1 come un primo, diversamente da noi ora; come conseguenza, ora noi escluderemmo i numeri 3 = 1 + 1 + 1 e 4 = 2 + 1 + 1.
Eulero propose una congettura più forte: ogni numero pari maggiore di 2 è la somma di due primi. Per esempio, 4 = 2 + 2, 6 = 3 + 3, 8 = 5 + 3, 10 = 5 + 5 e così via. Questa congettura implica quella di Goldbach. Eulero era sicuro che la sua congettura fosse vera, ma non fu in grado di trovare una dimostrazione, e la congettura è ancora aperta. Esperimenti condotti al computer hanno mostrato che è vera per ogni numero pari minore o uguale a 1018. Il migliore risultato noto è stato ottenuto da Chen Jing-Run nel 1973, con l’ausilio di complicate tecniche analitiche. Questi ha dimostrato che ogni numero pari sufficientemente grande è la somma di due primi, o di un primo e un quasi-primo (il prodotto di due primi).
La congettura dei primi gemelli è molto più antica, e risale a Euclide. Afferma che esiste un numero infinito di primi gemelli p e p + 2. Esempi di primi gemelli sono 5, 7 e 11, 13. Anche in questo caso, non è nota una dimostrazione né una confutazione. Nel 1966, Chen ha dimostrato che esiste un numero infinito di primi p, tali che p + 2 è primo oppure quasi-primo. Attualmente, i primi gemelli più grandi conosciuti sono 2.003.663.613 × 2195.000 ± 1, trovati da Eric Vautier, Patrick McKibbon e Dmitri Gribenko nel 2007.
Il risultato è che un numero è la somma di due quadrati se e soltanto se ogni divisore primo della forma 4k − 1 compare a una potenza pari. Usando metodi simili, nel 1770 Giuseppe Luigi Lagrange dimostrò che ogni intero positivo è la somma di quattro quadrati perfetti (includendo uno o più 0 se necessario). Fermat aveva in precedenza enunciato questo risultato, ma non si è trovata traccia della dimostrazione.
Una delle scoperte più importanti di Fermat è allo stesso tempo una delle più semplici. È nota come piccolo teorema di Fermat, per distinguerlo dal suo ultimo (talvolta chiamato grande) teorema, e afferma che se p è un qualsiasi primo e a un qualsiasi numero intero, allora ap − a è un multiplo di p. La proprietà corrispondente è generalmente falsa se p è composto, ma non sempre.
Il risultato più celebre di Fermat richiese 350 anni per una dimostrazione. Fermat lo enunciò intorno al 1640, e sostenne di avere una dimostrazione, ma tutto quello che abbiamo del suo lavoro è una breve annotazione. Fermat possedeva una copia dell’Arithmetica di Diofanto, che era stata di ispirazione per molti dei suoi studi, ed era solito annotare le proprie idee sul margine del volume. A un certo punto forse rifletteva sull’equazione di Pitagora: sommare due quadrati per ottenere un quadrato. Si domandò che cosa sarebbe successo se invece di quadrati si fossero sommati cubi, ma non trovò alcuna soluzione. Lo stesso problema sorse per potenze quarte, quinte o superiori.
Nel 1670, il figlio di Fermat, Samuel, pubblicò
un’edizione della traduzione di Bachet dell’Arithmetica,
che includeva le note a margine scritte da Fermat. Una di queste
note divenne famosa: l’affermazione che se  la somma di
due potenze n-esime non è mai una potenza
n-esima. La nota a margine dice: «È impossibile separare
un cubo in due cubi, o una potenza quarta in due potenze quarte, o
in generale, tutte le potenze maggiori di due come somma della
stessa potenza. Dispongo di una meravigliosa dimostrazione di
questo teorema, che non può essere contenuta nel margine troppo
stretto della pagina».
la somma di
due potenze n-esime non è mai una potenza
n-esima. La nota a margine dice: «È impossibile separare
un cubo in due cubi, o una potenza quarta in due potenze quarte, o
in generale, tutte le potenze maggiori di due come somma della
stessa potenza. Dispongo di una meravigliosa dimostrazione di
questo teorema, che non può essere contenuta nel margine troppo
stretto della pagina».
Sembra poco probabile che la sua dimostrazione, se esisteva, fosse corretta. La prima, e attualmente unica, dimostrazione è giunta nel 1994 a opera di Andrew Wiles: usa metodi astratti avanzati che non esistevano prima della fine del XX secolo.
Dopo Fermat, molti matematici di spicco si dedicarono alla teoria dei numeri, in particolare Eulero e Lagrange. La maggior parte dei teoremi che Fermat aveva enunciato ma non dimostrato furono affrontati in questo periodo.
Pierre de Fermat (1601-1665)
Pierre Fermat nacque a Beaumont-de-Lomagne in Francia nel 1601, figlio del mercante di cuoio Dominique Fermat e di Claire de Long, figlia di una famiglia di avvocati. Nel 1629 aveva fatto importanti scoperte in geometria, ed era stato un precursore dell’analisi infinitesimale, ma scelse la carriera legale, e nel 1631 divenne consigliere al Parlamento di Tolosa. Questo lo autorizzò ad aggiungere il «de» al suo cognome. Quando un’epidemia di peste uccise i suoi superiori, fece rapidamente carriera. Nel 1648 divenne consigliere del re al parlamento di Tolosa, e mantenne tale carica per il resto della vita, raggiungendo nel 1652 il più alto livello della Corte Criminale.
Non ricoprì mai incarichi accademici, ma la matematica fu la sua passione. Nel 1653 si ammalò di peste, si vociferò della sua morte, ma sopravvisse. Intrattenne una fitta corrispondenza con altri intellettuali, in particolare il matematico Pierre de Carcavi e il monaco Marin Mersenne.
Si occupò di meccanica, ottica, probabilità e geometria, e il suo metodo per individuare i valori massimi e minimi di una funzione aprì il terreno all’analisi infinitesimale. Divenne uno dei più eminenti matematici al mondo, ma pubblicò poco del suo lavoro, soprattutto perché non voleva perdere tempo a prepararlo per la pubblicazione.
Il suo principale influsso, che durò nel tempo,
fu nell’ambito della teoria dei numeri, dove egli sfidò altri
matematici a dimostrare una serie di teoremi e a risolvere vari
problemi. Tra questi vi era l’«equazione di Pell» (così detta per
errore) nx2 + 1 = y2, e
l’affermazione che la somma di due cubi perfetti diversi da zero
non può essere un cubo perfetto. Questo è un caso particolare di
una congettura più generale, «l’ultimo teorema di Fermat», in cui i
cubi sono sostituiti dalle potenze n-esime per ogni 
Morì nel 1665, appena due giorni dopo aver portato a termine un procedimento legale.
Gauss
Il successivo passo avanti nella teoria dei numeri fu compiuto da Gauss, che pubblicò il suo capolavoro, le Disquisitiones arithmeticae, nel 1801. Questo libro portò la teoria dei numeri al centro della scena matematica, rendendola un elemento fondamentale del pensiero matematico prevalente. Gauss si concentrò soprattutto sul suo nuovo lavoro, ma gettò le basi della teoria dei numeri e riordinò in maniera sistematica le idee dei suoi predecessori.
Carl Friedrich Gauss (1777-1855)
Gauss fu molto precoce, e a quanto si racconta cominciò a correggere l’aritmetica del padre all’età di tre anni. Nel 1792, con il supporto economico del duca di Brunswick-Wolfenbüttel, Gauss entrò nel Collegium Carolinum di Brunswick. Qui fece diverse importanti scoperte matematiche, tra cui la legge della reciprocità quadratica e il teorema dei numeri primi, ma non le dimostrò. Nel periodo 1795-1798 studiò a Göttingen, dove scoprì come costruire con riga e compasso un poligono regolare con 17 lati. Le sue Disquisitiones arithmeticae, ad oggi l’opera più importante nel campo della teoria dei numeri, furono pubblicate nel 1801.
La notorietà di Gauss, ad ogni modo, è dovuta alle previsioni astronomiche. Nel 1801 Giuseppe Piazzi aveva scoperto il primo asteroide: Ceres. Le osservazioni erano così rare che gli astronomi temevano di non riuscire a individuarlo nuovamente quando fosse riapparso non più coperto dal Sole. Molti astronomi predissero dove sarebbe riapparso, e lo stesso fece Gauss. Soltanto Gauss aveva ragione. In effetti, Gauss aveva usato un metodo di sua invenzione, ora chiamato «metodo dei minimi quadrati», per ricavare risultati accurati da osservazioni limitate. All’epoca Gauss non rivelò la sua tecnica, ma da allora questa è diventata fondamentale nella scienza statistica e delle osservazioni.
Nel 1805 Gauss sposò Johanna Ostoff, che amò profondamente, e nel 1807 lasciò Brunswick per accettare la direzione dell’osservatorio di Göttingen. Nel 1808 suo padre morì, e nel 1809 morì Johanna dopo aver dato alla luce il loro secondo figlio. Poco tempo dopo morì anche il figlio.
Nonostante queste tragedie personali, Gauss proseguì i suoi studi, e nel 1809 pubblicò la sua Theoria motus corporum cælestium in sectionibus conicis solem ambientium, un contributo fondamentale alla meccanica celeste. Si sposò di nuovo, con Minna, una cara amica di Johanna, ma il matrimonio fu più di convenienza che di amore.
Intorno al 1816 Gauss scrisse una rassegna di deduzioni dell’assioma delle parallele dagli altri assiomi di Euclide, in cui accennava a un’idea che aveva probabilmente sviluppato già dal 1800, cioè la possibilità di una geometria coerente dal punto di vista logico, e diversa da quella di Euclide.
Nel 1818 fu incaricato di eseguire un rilevamento geodetico di Hannover, e contribuì notevolmente ai metodi usati nelle misurazioni. Nel 1831, dopo la morte di Minna, Gauss intraprese, in collaborazione con il fisico Wilhelm Weber, gli studi sul campo magnetico terrestre.
Scoprirono quelle che sono ora note come leggi di Kirchhoff per i circuiti elettrici, e costruirono un telegrafo rozzo ma funzionante. Quando nel 1837 Weber fu costretto a lasciare Göttingen, il lavoro scientifico di Gauss ebbe una battuta di arresto, anche se il matematico mantenne l’interesse per il lavoro di altri, in particolare Ferdinand Eisenstein e George Bernhard Riemann. Morì tranquillamente nel sonno.
Il più importante di questi nuovi concetti fondamentali fu un’idea molto semplice ma potente: l’aritmetica modulare. Gauss scoprì un nuovo tipo di sistema di numeri, analogo agli interi ma differente per un aspetto fondamentale: un numero particolare, detto modulo, era identificato con il numero zero. Questa singolare idea si rivelò importantissima per lo studio delle proprietà di divisibilità degli interi ordinari.
Vediamo l’idea di Gauss. Dato un intero m, diciamo che a e b sono congruenti al modulo m, e scriviamo
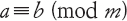
se la differenza a − b è divisibile esattamente per m. L’aritmetica modulo m funziona allora esattamente come l’aritmetica ordinaria, tranne per il fatto che in ogni operazione dobbiamo sostituire m con 0. Di conseguenza, ogni multiplo di m può essere ignorato.
Per comprendere lo spirito dell’aritmetica di Gauss, si usa in genere l’espressione «aritmetica dell’orologio». In un orologio, il numero 12 equivale di fatto allo 0 perché le ore si ripetono dopo 12 passi (24 nell’Europa continentale e per le attività militari). Sette ore dopo le 6, l’orologio non segna le 13, ma l’1, e nel sistema di Gauss 13 ≡ 1 (mod 12). L’aritmetica modulare si comporta dunque come un orologio che impiega m ore per completare un giro. Non sorprende che l’aritmetica modulare entri in gioco ogni volta che i matematici osservano fenomeni che mutano secondo cicli ripetitivi.
Le Disquisitiones arithmeticae introdussero l’aritmetica modulare come fondamento per idee più complesse, e qui ne citiamo tre.
Il cuore del libro estende ampiamente le osservazioni di Fermat sul fatto che i primi della forma 4k + 1 sono esprimibili come somma di due quadrati, mentre quelli della forma 4k − 1 non lo sono. Gauss enunciò nuovamente questo risultato come caratterizzazione di interi che possono essere scritti nella forma x2 + y2, con x e y interi. Si domandò poi che cosa succede se al posto di questa formula usiamo una forma quadratica generale, ax2 + bxy + cy2. Gauss sviluppò a tale proposito teoremi troppo tecnici da discutere in questa sede, ma giunse a comprendere la questione in maniera quasi completa.
Un altro tema affrontato nelle Disquisitiones arithmeticae riguarda la legge della reciprocità quadratica, che impegnò e angosciò Gauss per molti anni. Il punto di partenza è un semplice problema: come appaiono i quadrati perfetti in relazione a un modulo dato? Supponiamo, per esempio, che il modulo sia 11. In questo caso i quadrati perfetti possibili (dei numeri minori di 11) sono
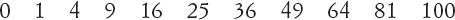
che, modulo 11, si riducono all’elenco

in cui ogni numero diverso da zero compare due volte. Questi numeri rappresentano i residui quadratici, modulo 11.
La chiave per risolvere la questione consiste nell’osservare i numeri primi. Se p e q sono primi, quando q è un quadrato (mod p)? Gauss scoprì che mentre non esiste una maniera semplice di rispondere direttamente alla domanda, nasce un importante collegamento con un’altra domanda: quando p è un quadrato (mod q)? Per esempio, l’elenco precedente dei residui quadratici mostra che q = 5 è un quadrato modulo p = 11. È anche vero che 11 è un quadrato modulo 5, perché 11 ≡ 1 (mod5) e 1 = 12. Ne consegue che entrambe le domande hanno la stessa risposta.
Gauss dimostrò che questa legge di reciprocità vale per ogni coppia di primi dispari, tranne quando entrambi i primi sono della forma 4k − 1, nel qual caso le due questioni hanno sempre risposta opposta. Vale a dire che per ogni coppia di primi dispari p e q,
q è un quadrato (mod p) se e solo se p è un quadrato (mod q)
a meno che sia p che q non siano della forma 4k − 1, nel qual caso
q è un quadrato (mod p) se e solo se p non è un quadrato (mod q).
In principio Gauss non si accorse che l’osservazione non era nuova: Eulero aveva individuato la stessa relazione. Diversamente da Eulero però, Gauss riuscì a dimostrare che questo è sempre vero. La dimostrazione si rivelò molto difficile, e Gauss dovette impegnarsi molti anni per colmare una piccola ma fondamentale lacuna.
Un terzo argomento trattato nelle Disquisitiones è la scoperta che aveva convinto Gauss a diventare matematico all’età di 19 anni: una costruzione geometrica per un poligono regolare con 17 lati (17-gono). Euclide aveva fornito costruzioni, usando riga e compasso, per poligoni regolari con tre, cinque e quindici lati; sapeva anche che quei numeri potevano essere ripetutamente raddoppiati bisecando gli angoli, per ottenere poligoni regolari con quattro, sei, otto e dieci lati, e così via. Euclide però non aveva proposto alcuna costruzione per poligoni con sette lati, nove o numeri diversi da quelli appena detti. Per circa duemila anni, il mondo matematico aveva assunto che Euclide avesse detto l’ultima parola, e non si potesse costruire nessun altro poligono regolare. Gauss dimostrò che non era vero.
È facile vedere che il problema principale consiste nel costruire p-goni regolari dove p è primo. Gauss sottolineò che tale costruzione è equivalente a risolvere l’equazione algebrica
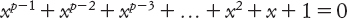
Ora, una costruzione con riga e compasso si può vedere, grazie alla geometria delle coordinate, come una successione di equazioni quadratiche. Se una costruzione di questo tipo esiste, segue (in maniera non del tutto banale) che p − 1 deve essere una potenza di 2.
I casi greci p = 3 e 5 soddisfano questa condizione: in questo caso p − 1 = 2 e 4, rispettivamente. Non sono però gli unici numeri primi di questo tipo; per esempio 17 − 1 = 16 è una potenza di 2. Questo non dimostra affatto che il 17-gono sia costruibile, ma fornisce un forte indizio, e Gauss fece in modo di trovare una riduzione esplicita di questa equazione di sedicesimo grado a una serie di quadratiche. Affermò, ma non dimostrò, che una costruzione è possibile ogni volta che p − 1 è una potenza di 2 (sempre con la condizione che p sia primo), ed è impossibile per tutti gli altri primi. La dimostrazione fu presto completata da altri.
Questi primi speciali sono detti primi di Fermat, perché furono studiati da Fermat, il quale osservò che se p è primo e p − 1 = 2k, allora anche k deve essere una potenza di 2. Cominciò a scrivere i primi di Fermat: 2, 3, 5, 17, 257, e 65 537. Ipotizzò che i numeri della forma 22m + 1 fossero sempre primi, ma questo si rivelò sbagliato. Eulero scoprì che se m = 5 il numero è divisibile per il fattore 641.
Ne consegue che deve anche essere possibile una costruzione con riga e compasso per le figure regolari 257-gono e 65 537-gono. Friedrich J. Richelot costruì nel 1832 il 257-gono regolare, e il suo lavoro è risultato corretto. Johann Hermes dedicò dieci anni allo studio del 65 537-gono, e completò la sua costruzione nel 1894. Studi recenti suggeriscono che questo lavoro contenga alcuni errori.
Quello che la teoria dei numeri fece per loro
Una delle prime applicazioni pratiche della teoria dei numeri riguarda gli ingranaggi. Se due ruote dentate sono accoppiate in modo che i loro denti possano ingranare, e una ruota ha m denti, l’altra n, allora il movimento delle ruote è in relazione con questi numeri. Supponiamo, per esempio, che una ruota abbia 30 denti e che l’altra ne abbia 7. Se la ruota grande completa un intero giro, che cosa fa la ruota più piccola? Ritorna nella posizione iniziale dopo 7, 14, 21 e 28 passi. Dunque, i 2 passi finali, per arrivare a 30, la fanno avanzare proprio di 2 passi. Questo è esattamente il numero che si ottiene come resto dividendo 30 per 7. Il movimento delle ruote dentate è dunque la base dell’aritmetica modulare.
Le ruote dentate furono usate dagli artigiani greci per progettare uno straordinario congegno, il meccanismo di Antikythera. Nel 1900, nei pressi dell’isola di Antikythera e alla profondità di circa 40 metri, il pescatore di spugne Elias Stadiatis trovò un blocco informe di pietra consumata in un relitto risalente al 65 a.C. Nel 1902 l’archeologo Valerios Stais scoprì che la pietra nascondeva all’interno un ingranaggio, che era in realtà quello che rimaneva di un elaborato meccanismo in bronzo. Riportava alcune iscrizioni in alfabeto greco. Studiandone la struttura e le iscrizioni, il meccanismo risultò essere un calcolatore astronomico, formato da più di 30 ruote dentate (l’ultima ricostruzione del 2006 ipotizza che in origine le ruote fossero 37). Il numero di ruote corrisponde a importanti rapporti astronomici. In particolare, due ruote hanno 53 denti (un numero difficile da riportare in un manufatto) e questo numero deriva dalla velocità di rotazione del punto sulla Luna più lontano dalla Terra. Tutti i fattori primi dei numeri di denti sono basati su due cicli astronomici classici, i cicli di Metone e di Saros. L’analisi a raggi X ha rivelato nuove iscrizioni permettendone la lettura, ed è ora certo che il dispositivo fosse usato per prevedere le posizioni del Sole, della Luna e forse dei pianeti allora noti. Le iscrizioni risalgono al 150-100 a.C. circa.
Il meccanismo di Antikythera è il risultato di un progetto sofisticato, e sembra tener conto della teoria del moto della Luna sviluppata da Ipparco; potrebbe essere stato costruito da uno dei suoi allievi, o almeno con il loro aiuto. Era forse un giocattolo di lusso per un personaggio reale, piuttosto che uno strumento di utilità pratica, e questo potrebbe spiegarne la raffinata progettazione e la pregiata fattura.
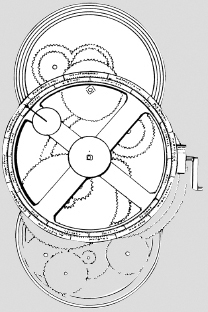
Una ricostruzione del meccanismo di Antikythera
La teoria dei numeri cominciò a diventare interessante dal punto di vista matematico con il lavoro di Fermat, che mise a fuoco alcuni degli importanti modelli nascosti nello strano e incomprensibile comportamento dei numeri interi. La sua spiacevole abitudine di non fornire dimostrazioni fu compensata da Eulero, Lagrange e altri personaggi di minore rilevanza, con l’unica eccezione del suo ultimo teorema, ma la teoria dei numeri sembra consistere di teoremi isolati, spesso profondi e difficili, ma non molto collegati l’uno all’altro.
Tutto questo cambiò quando Gauss entrò in scena e pose basi concettuali generali per la teoria dei numeri, come l’aritmetica modulare. Stabilì anche un collegamento tra la teoria dei numeri e la geometria, con il suo lavoro sui poligoni regolari. Da quel momento, la teoria dei numeri divenne una caratteristica portante nel corpus della matematica.
Marie-Sophie Germain (1776-1831)
Sophie Germain era figlia del mercante di seta Ambroise-François Germain e di Marie-Madeleine Gruguelin. All’età di tredici anni lesse della morte di Archimede, ucciso da un soldato romano mentre contemplava uno schema geometrico disegnato sulla sabbia, ed ebbe l’ispirazione a diventare una matematica. Nonostante i suoi genitori, pur con le migliori intenzioni, tentassero di dissuaderla – allora la matematica non era considerata una vocazione conveniente per una giovane donna – Sophie lesse le opere di Newton e di Eulero, avvolta in una coperta mentre la madre e il padre dormivano. Quando i genitori si convinsero della sua passione per la matematica, acconsentirono a lasciarla studiare e la sostennero, finanziandola per tutta la vita.
Riuscì a ottenere le dispense delle lezioni dall’École Polytechnique, e presentò a Lagrange alcuni suoi lavori originali sotto il nome di «Monsieur LeBlanc». Lagrange, molto colpito dalla qualità degli elaborati, alla fine scoprì che erano opera di una donna, ed ebbe il buon senso di incoraggiarla diventandone l’ispiratore. I due collaborarono nelle ricerche, e alcuni dei risultati di Sophie vennero presentati in un’edizione successiva dell’Essai sur la Théorie des nombres di Legendre, pubblicato in origine nel 1798.
Il suo più famoso corrispondente fu Gauss. Sophie studiò le Disquisitiones arithmeticae, e dal 1804 al 1809 scrisse molte lettere al suo autore, sempre celando la propria identità con il nome di LeBlanc. Nelle sue lettere indirizzate ad altri matematici Gauss elogiò il lavoro di LeBlanc, e nel 1806, quando i francesi occuparono Brunswick, scoprì che questi era in realtà una donna. Temendo che a Gauss potesse toccare la stessa sorte di Archimede, Sophie contattò un amico di famiglia che era un ufficiale di grado elevato nell’esercito francese, il generale Pernety. Gauss lo venne a sapere, e scoprì che LeBlanc era in realtà Sophie.
Sophie non aveva motivo di preoccuparsi. Gauss fu ancora più colpito, e le scrisse:
Ma come esprimerVi la mia ammirazione e stupore nello scoprire la metamorfosi del mio stimato corrispondente Monsieur LeBlanc in questo illustre personaggio […] Quando una persona del sesso che, a causa delle nostre abitudini e dei nostri pregiudizi, incontra molti più ostacoli di un uomo nel familiarizzarsi con problemi complessi, supera tuttavia queste barriere e penetra nelle profondità più recondite, allora senza dubbio rivela di possedere il coraggio più nobile, un talento straordinario e un genio superiore.
Sophie ottenne alcuni risultati sull’ultimo teorema di Fermat, i più notevoli alla data del 1840. Tra il 1810 e il 1820 studiò le vibrazioni delle superfici, un problema posto dall’Institut de France. In particolare, si impegnò a spiegare le «configurazioni di Chladni», disegni simmetrici che compaiono quando si versa sabbia fine su una lastra metallica, messa poi in vibrazione con un archetto. Al suo terzo tentativo le fu conferita una medaglia d’oro, anche se per ragioni ignote, forse una protesta nei confronti dell’ingiusto trattamento riservato alle donne di scienza, non si presentò alla cerimonia di premiazione.
Nel 1829 si ammalò di tumore al seno, ma continuò a studiare la teoria dei numeri e la curvatura delle superfici fino alla sua morte, che avvenne due anni dopo.
Quello che la teoria dei numeri fa per noi
La teoria dei numeri è alla base di molti codici di sicurezza importanti usati per il commercio su Internet. Il più famoso di questi codici è il criptosistema RSA (Ronald Rivest, Adi Shamir e Leonard Adleman), che ha una sorprendente caratteristica in quanto il metodo usato per cifrare i messaggi può essere reso pubblico senza fornire la procedura inversa di decodifica.
Supponiamo che Alice voglia inviare un messaggio segreto a Bob. Prima di farlo, i due scelgono insieme due numeri primi grandi, p e q (con almeno un centinaio di cifre) e li moltiplicano tra loro ottenendo M = pq. Se vogliono, possono comunicare pubblicamente questo numero. Calcolano poi K = (p − 1)(q − 1), ma mantengono segreto il risultato.
Ora Alice rappresenta il suo messaggio come un numero x nell’intervallo compreso tra 0 e M (o una serie di numeri di questo tipo se si tratta di un messaggio lungo). Per cifrare il messaggio, Alice sceglie un certo numero a, che non ha fattori in comune con K, e calcola y ≡ xa (mod M). Il numero a deve essere noto a Bob, e può anche essere reso pubblico.
Per decifrare i messaggi, Bob deve conoscere un numero b tale che ab ≡ 1mod K. Questo numero (che esiste ed è unico) è tenuto segreto. Per decifrare y, Bob calcola
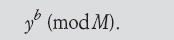
Perché questo serve alla decodifica? Perché
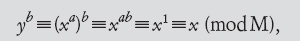
usando una generalizzazione dovuta a Eulero del piccolo teorema di Fermat.
Questo metodo è pratico perché disponiamo di procedure efficienti per trovare numeri primi grandi. Non conosciamo però ancora nessun metodo per trovare in maniera altrettanto efficiente i fattori primi di un numero grande. Di conseguenza, la conoscenza del prodotto pq non basta per trovare p e q, e senza questi valori non è possibile ricavare il valore di b, necessario per decifrare il messaggio.
Le intuizioni di Gauss portarono a individuare in matematica nuovi tipi di strutture: nuovi sistemi numerici, come gli interi mod n, e nuove operazioni, come la composizione di forme quadratiche. Guardando in retrospettiva, la teoria dei numeri del periodo a cavallo tra il XVIII e il XIX secolo condusse all’algebra astratta della fine del XIX e del XX secolo. I matematici stavano iniziando ad ampliare l’insieme di concetti e strutture accettabili come oggetti di studio. Nonostante il tema specifico, le Disquisitiones arithmeticae rappresentano un’importante pietra miliare nello sviluppo dell’impostazione moderna di tutta la matematica. Anche per questo motivo Gauss gode di una fama così alta tra i matematici.
Fino alla fine del XX secolo, la teoria dei numeri è stata considerata una branca della matematica pura, interessante di per sé, e per le sue numerose applicazioni all’interno della matematica stessa, ma con poca importanza reale nel mondo esterno. Tutto questo è cambiato con l’invenzione delle comunicazioni digitali alla fine del XX secolo. Poiché da allora la comunicazione ha fatto affidamento sui numeri, non sorprende affatto che la teoria dei numeri abbia avuto risalto in quelle aree di applicazione. Spesso occorre tempo perché un’idea matematica valida acquisisca interesse pratico (a volte occorrono centinaia di anni), ma alla fine molti concetti che i matematici ritengono interessanti per puri scopi speculativi mostrano un’applicazione utile anche nel mondo reale.