Una de mis características menos simpáticas es la de que me enfado cuando se hace mal una cita, sobre todo si es de Shakespeare.

Una manera segura de provocar en mí síntomas de apoplejía es que alguien que esté haciendo una interpretación cómica del pasaje de Romeo y Julieta diga Wherefore art thou, Romeo? (¿Por qué estás aquí, Romeo?) con una entonación y unos ademanes que indiquen que el significado es Where are you, Romeo? (¿Dónde estás, Romeo?).

Esto no sólo indica que los pobres ignorantes responsables no leyeron nunca la obra, sino también que ni siquiera saben el significado de wherefore o, peor aún, presumen que el auditorio tampoco lo sabe ni le importa.

También merecen mención especial —en la lista de los que dan citas equivocadas y por ello me repelen— los que hablan de «dorar el lirio».

Es una cita errónea del Rey Juan, de Shakespeare, acto IV, escena II, donde el conde de Salisbury expresa seis acciones que representan «excesos ruinosos y ridículos», como una manera de condenar la insistencia del rey Juan en una segunda coronación. En cada caso, se describe algo que trata de mejorar lo que no puede ser mejorado, y los dos primeros ejemplos son «dorar el oro refinado y pintar el lirio».

El que cita mal, contrae las dos cosas y dice «dorar el lirio», acción que no tiene toda la exquisita inadecuación de las dos acciones expresadas por Shakespeare.

Así, para combatir este fastidio, intento mostrar una manera en la que puedo «desdorar el oro refinado». Más adelante veréis a lo que me refiero.

Cuando estoy atrapado en una reunión, inquieto, y estoy seguro de que nadie me observa atentamente, a veces puedo liberarme jugando con números: sumando, restando, multiplicando, dividiendo, etcétera.

Comprenderéis que esto lo hago sin objeto, puesto que carezco de todo talento matemático. Lo que hago con los números es a las Matemáticas lo que poner un cubo de juguete sobre otro es a la arquitectura. Pero sucede que no considero que haga Matemáticas; estoy, simplemente, protegiendo mi cerebro (órgano bastante exigente) de alguna avería por causa del tedio. Hacía esto desde muy temprana edad, creo que tendría unos doce años, y estudiaba la relación de los números con sus cuadrados de la manera siguiente:

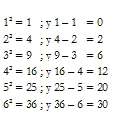
Entonces advertí la regularidad. Si se asciende por la escala de números enteros sustrayendo cada uno de éstos de su cuadrado, el primer entero dará 0. Entonces hay que sumar 2 para obtener 2 en el siguiente número entero; sumar 4 para obtener 6, sumar 6 para obtener 12; sumar 8 para obtener 20; sumar 10 para obtener 30.

Al producir los números sucesivos, se asciende por la escala de números enteros de un modo regular, de manera que sabía que el número siguiente sería 42, después 56 y luego 72, sin tener que hacer las sustracciones: 49 - 7; 64 - 8, y 81 - 9. Estaba muy orgulloso de mí mismo.

Después intenté algo más. Escribí cada número entero y coloqué a continuación del mismo la cifra que obtenía, restándolo de su cuadrado, y entonces consideré de qué otra manera podía representar la cifra. Así:

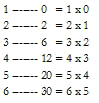
Me parecía claro que cada número entero restado de su propio cuadrado daba un resultado que era igual al mismo número entero multiplicado por el inmediatamente anterior. Y mi corazón de doce años latió más de prisa, pues concebía la idea de que había descubierto algo muy raro, que quizá nadie había advertido hasta entonces. (Ya os he dicho que no tengo talento matemático. Me imagino que un verdadero matemático habría advertido esto a los tres años de edad y lo habría descartado por evidente).

En todo caso, yo quise generalizarlo, pues entonces me hallaba estudiando álgebra. Por consiguiente, designé un entero, cualquier entero, como «x». El número entero inmediatamente anterior sería «x - 1» y el cuadrado del número entero sería «x²».

Resultó, pues, que había descubierto, gracias al gran poder de mi cerebro, que un entero restado de su cuadrado, «x²» —era igual a aquel entero multiplicado por el inmediatamente menor, «x (x - 1)». Dicho de otra manera:

x² — x = x (x – 1)

Con esto desapareció toda mi alegría, pues esta ecuación era tan evidente, que no podía serlo más. Me limitaba a emplear como factor la «x» del lado izquierdo, y esto me daba el lado derecho. El valor de mi descubrimiento era igual al de encontrar que dos docenas equivalían a veinticuatro.

Por consiguiente, abandoné aquella línea particular de descubrimiento y nunca volví a ella. Y fue una lástima, pues si hubiese continuado observando, tal vez habría descubierto algo que, sin ser precisamente nuevo, habría sido mucho más interesante que la ecuación que acabo de exponeros. Y como ahora tengo un poco más de doce años, puedo hacerlo… Conque, ¡vamos allá!

Consideremos el problema de restar un número entero de su cuadrado sólo en los primeros tres enteros: 1 – 1 = 0; 4 – 2 = 2; y 9 – 3 = 6.

Las diferencias siguen subiendo de un modo regular, de manera que podemos decir que no hay sustracciones de esta clase que puedan dar diferencias de 1, 3, 4 ó 5. Al menos, si nos limitamos a números enteros. Sin embargo, podemos pasar al empleo de fracciones decimales:

Por ejemplo, el cuadrado de 1,1 es 1,21, y 1,21 - 1,1 = 0,11, mientras que el cuadrado de 1,2 es 1,44, y 1,44 - 1,2 = 0,24.

Si seguimos subiendo por décimos, encontramos que el cuadrado de 1,6 es 2,56, y 2,56 - 1,6 = 0,96, que es una cifra muy próxima a 1.

Tenemos también que el cuadrado de 2,3 es 5,29, y 5,29 - 2,3 = 2,99, que es todavía más próximo a 3.

De hecho, podemos pensar, ahora, si elegimos la fracción decimal adecuada, podemos restarla de su cuadrado y obtener un número muy próximo al entero que elijamos. Así, el cuadrado de 4,65 es 21,6225, y 21,6225 - 4,65 = 16,9725, cifra muy próxima a 17.

Ninguno de los ejemplos que he citado da una diferencia que sea un número entero exacto; sólo se le acerca. Si mi cerebro de doce años hubiese trabajado en esto y sido tan inteligente como yo hubiera deseado, podría haber pensado que, sumando más decimales, podía dar de lleno con un número entero. Si 2,32 - 2,3 = 2,99, sería lógico esperar que un pequeño aumento en 2,3 nos daría exactamente 3. Por ejemplo, 2,3032 - 2,303 = 3,000809. Ahora me he pasado una pizca, por consiguiente, bajo a 2,302752 - 2,30275 = 2,9999075.

Cuando yo tenía doce años, no disponía de ninguna calculadora de bolsillo, por lo cual habría tardado mucho tiempo en sacar las anteriores relaciones, habría cometido muchos errores aritméticos y me habría fatigado. Pronto habría desistido.

Pero supongamos que no hubiese desistido. Supongamos que hubiese tenido agallas y constancia para probar con más y más números decimales y llenar más y más hojas de papel con enormes cálculos. Habría descubierto que, por mucha atención que prestase al intentarlo y por muchas horas (o años) que pasase en ello, nunca encontraría ningún número con cualquier cantidad de decimales que, al ser restado de su cuadrado, diese exactamente un número 3. Me acercaría cada vez más, pero nada me situaría exactamente en 3.

De esto habría podido sacar dos conclusiones posibles: 1) Si hubiese sido un muchacho corriente, habría decidido que carecía de la constancia necesaria para encontrar el decimal definitivo. 2) Si hubiese sido un chico con alma de matemático, habría saltado intuitivamente a la noción de que el número que buscaba era, en realidad, un decimal infinito y no repetible, y habría tenido así mi primer atisbo —sin ayuda— de los números irracionales. (Por desgracia, nunca fui lo bastante inteligente como para llegar al punto de tener que elegir; por lo visto, era menos que corriente).

Al seguir con el álgebra, descubrí cómo resolver la «x» en ecuaciones del tipo siguiente: «ax² + bx + c = 0». En tal ecuación, «a», «b», y «c», los «coeficientes», son números enteros, y «x» es la incógnita. Resulta que en tal ecuación:

x = (½ a) (-b + ²R[b2 – 4ac]) — ecuación 1

Dos aclaraciones: en la ecuación 1, la cantidad de un paréntesis tiene que ser multiplicada por la cantidad que hay en el otro paréntesis. Además, el símbolo «²R» representa «raíz cuadrada». La «raíz cuadrada de x», o «²R[x]», es el número que, si se multiplica por sí mismo, da «x». Así, ²R[25] = 5, ²R[81] = 9, etcétera. (Otra observación: Si el signo más de la ecuación 1 es sustituido por un signo menos, podría darse una segunda respuesta posible, pero aquí emplearemos sólo el signo más). Para dar un ejemplo de cómo funciona la ecuación 1, supongamos una ecuación como «x² + 8x – 5». En tal caso, «c» es igual a [ - 5 ] y «b» es igual a [ + 8 ]. Sin embargo, el signo más se omite generalmente en estos casos y se da por «sobrentendido», de manera que se dice que «b» es simplemente igual a 8.

Pero, ¿qué es «a», el coeficiente de «x²», en la ecuación «x² + 8x - 5»? Podría parecer que la «x²» de aquella ecuación no tiene ningún coeficiente, pero no es así. La «x²» que permanece sola es en realidad «1x²», pero el 1 se da por entendido y, generalmente, se omite. Sin embargo, en este caso, «a» se considera igual a 1. (Personalmente, yo no omitiría nunca nada y siempre escribiría 8 como + 8, y «x²» como «1x²», y, ¿por qué no?, «x» como «x¹»; pero los matemáticos no lo hacen así. Es su simpática manera de ahorrarse trabajo a costa de hacer las cosas algo más confusas para los principiantes, y no se puede luchar contra la Facultad).

Ahora estamos en condiciones de volver al asunto de restar un número entero de su cuadrado para obtener alguna cantidad deseada. Podemos generalizar el problema algebraico suponiendo que «x» es cualquier número entero; «x²», su cuadrado, e «y», el número entero que representa la diferencia. Entonces escribiremos:

x² — x = y

Para hacerlo más interesante, escojamos un número entero para «y», y así podremos ver cómo funciona; y, para hacerlo más sencillo, escojamos el entero más pequeño: 1. La ecuación se convierte en:

x² — x = 1

Es posible restar 1 de cada lado del signo igual sin que cambie el resultado de la ecuación. (Este es el resultado de uno de los buenos y viejos axiomas: Los iguales sustraídos de iguales dan iguales).

Si restamos 1 de cada lado del signo igual tendremos «x² — x - 1». Si restamos 1 del lado derecho, tendremos 1 - 1, que es igual a 0. Por consiguiente, podemos escribir la ecuación como:

x² — x – 1 = 0 — ecuación 2

Si resolvéis esta ecuación por «x», tendréis un número que, sustraído de su cuadrado, os dará exactamente 1.

Para este fin, emplearemos la ecuación 1. Por «a», el coeficiente de «x²», tenemos 1; por «b», el coeficiente de «x», tenemos —1, y por «c», el coeficiente final, tenemos de nuevo —1.

Como «b» es igual a —1, «—b» = —(-1), o + 1, que se escribe, simplemente, 1. También «b²» = —(-1), o + 1, o 1. Como «a» es igual a 1, tendremos que ½ a es igual a ½. Y como «a» = 1, y «c» = —1, 4ac es igual a 4(1) (-1) o —4, y 4ac es igual a —(-4), o + 4, o 4.

Pensando en todo esto, tenemos todo lo que necesitamos saber para sustituir por números los símbolos de la ecuación 1 (y perdonadme si no necesitabais esta explicación paso a paso). Por tanto, la ecuación 1 se convierte en:

x = ½ ( 1 + ²R[ 1 + 4 ] ) = 1 ( 1 + ²R[ 5 ])

Este es el número que, al ser restado de su cuadrado, nos dará una diferencia de exactamente 1.

Para expresar el número como un decimal ordinario, debéis tomar la raíz cuadrada de 5, sumar 1 y dividir la suma por 2.

Pero, ¿cuál es la raíz cuadrada de 5? ¿Cuál es el número que, multiplicado por sí mismo, nos da 5? Es, ¡ay!, un número irracional, un decimal infinito e irrepetible. Pero podemos acercarnos mucho si decimos que es 2,23606796… En realidad, nos acercamos bastante si suponemos que la raíz cuadrada de 5 es 2,236068. Si multiplicamos este número por si mismo, 2,236068 x 2,236068, tendremos 5,0000001, o sea, con sólo un error de una diezmillonésima.

Si sumamos 1 a la raíz cuadrada de 5 y dividimos la suma por 2, tenemos 1,618034. (Un valor todavía más correcto sería 1,61803398…, pero 1,618034 es suficiente para nuestros fines).

Si tomamos el cuadrado de este número, vemos que 1,18034 x 1,618034 = 2,618034, y la diferencia es 1.

En realidad, no es tan exacta: 1,618034 x 1,618034 = 2,618034025156. El exceso de 0,000000025156 es resultado de la insignificante inexactitud de la cifra 1,618034. Ningún decimal, por largo que sea, puede ser por completo exacto.

La única cifra verdaderamente exacta es ½ ( 1 + ²R[ 5 ] ). Si se eleva este número al cuadrado, cosa que puede hacerse sin grandes dificultades —pero os ahorraré la molestia—, obtendremos la cantidad de ½ ( 3 + ²R[ 5 ] ), que es mayor exactamente en 1.

Consideremos ahora los «recíprocos». Si dividimos 1 por cualquier número, obtendremos otro número que es recíproco al primero. Dicho en otras palabras: ½ es recíproco de 2; 1/3 es recíproco de 3; 1/17,25 es recíproco de 17,25, y, en general, «1/x» es recíproco de «x».

En vez de restar un número de su cuadrado, restemos un recíproco de su número. Empleando sólo números enteros, tendremos:

Salvo en el caso de 1, tendremos siempre una fracción; pero, una vez más, no tenemos que aferrarnos a los números enteros. Supongamos que queremos encontrar un número que, al restarle su recíproco, nos dé una diferencia exactamente de 1.

Naturalmente, tendrá que ser un numero que esté entre los enteros 1 y 2, de modo que la diferencia estará en alguna parte entre 0 y 1 1/2. Supongamos, por ejemplo, que tomamos el número 1,5. Su recíproco es 1/1,5. Como 1,5 = 3/2, y 1/1,5 = 2/3, tenemos 3/2 - 2/3 = 5/6, que está muy cerca de 1. Si pasamos a 1,6 y restamos 1/1,6, y si confiáis en mi aritmética, el resultado es 0,975, que está aún más cerca.

Sin embargo, si seguimos experimentando, pronto estaremos seguros de que no vamos a encontrar ningún decimal que pueda darnos exactamente 1, cuando se reste su recíproco. Volveremos a encontrarnos en el reino de los números irracionales.

Pasemos, pues, al álgebra, y escribamos una ecuación que represente el caso general:

x - 1/x = 1

Si multiplicamos cada lado de la ecuación por «x», el resultado de la ecuación no cambia (¡confiad en mí!) Como «x» veces «x» es «x²», «1/x» veces «x» es 1, y 1 vez «x» es «x», tenemos:

x² - 1 =x

Si restamos «x» de cada lado de la ecuación, tenemos:

x² – 1 — x = 0 , ó cambiando el orden, x² — x – 1 = 0

Pero ésta vuelve a ser la ecuación 2, y la solución para «x» será la misma que antes. Ya sabemos que 1/2 (1 + ²R[ 5 ]) es exactamente 1 menos que su cuadrado. Bueno, es también exactamente 1 más que su recíproco.

Para comprobarlo, tomemos 1,618034, aquella buena aproximación de 1/2 (1 + ²R[ 5 ]) Resulta que 1/1,618034 = 0,618034.

Probemos ahora otra vez. Imaginaos un rectángulo de 1 unidad de ancho y 2 unidades de largo. (No importa qué clase de unidades sean: pulgadas, metros, años luz o cualquier otra).

En aquel rectángulo, la longitud es, evidentemente, el doble de la anchura. Pero la longitud y la anchura juntas son 3 unidades, que equivalen a 1 y 1/2 veces la longitud.

Si el rectángulo es de 1 unidad por 3, entonces la longitud es 3 veces la anchura, pero la longitud y la anchura juntas son 4, y la suma sería 1 y 1/3 veces la longitud.

Si el rectángulo fuese de 1 por 4, después de 1 por 5, y sucesivamente, se obtendrían pares de cifras que serían 4 y 1 1/4, 5 y 1 1/5, etcétera. Los dos números se alejarían cada vez más en su valor.

¿Podemos encontrar un rectángulo donde los dos números sean de igual valor?

En tal caso, tendría que ser uno en que la anchura fuese de 1 unidad, y la longitud fuese de menos de 2 unidades (porque a 2 unidades, los dos números son ya desiguales).

Pasemos directamente al álgebra. Supongamos que la anchura del rectángulo es 1 unidad, y la longitud es de «x» unidades. Para expresar cuántas veces es «x» mayor que 1, dividimos «x» por 1 y escribimos «x/1» o, simplemente, «x».

La suma de la anchura y la longitud del rectángulo es «x + 1». Para expresar cuántas veces es esto mayor que la longitud, tenemos «(x+1)/x».

Estamos buscando una situación en la que estas dos longitudes relativas, o «razones», sean iguales, y para esto escribimos esta ecuación:

x = (x + 1)/x

Si multiplicamos ambos lados de la ecuación por «x», el resultado de la ecuación no cambia y tenemos:

x² = x + 1

Si restamos «x + 1» de ambos lados, tampoco cambiamos la naturaleza de la ecuación y tenemos:

x² — (x + 1) = 0

Podemos eliminar el paréntesis si tomamos el negativo de «x + 1» y lo expresamos como «— x – 1», de modo que tenemos:

x² — x – 1 = 0

y aquí está de nuevo la ecuación 2, con su solución acostumbrada.

Supongamos ahora que tenemos un rectángulo cuya anchura es de 1 unidad y cuya longitud es de 1,618034 unidades. Sumando la anchura y la longitud, tendríamos 2,618034. Desde luego, la longitud es 1,618034 veces mayor que la anchura, mientras que la suma de longitud y anchura serían 2,618034/ 1,618034, o sea, 1,618034 veces la longitud.

Fueron los antiguos griegos quienes descubrieron esto. Esencialmente, era una manera de dividir una línea dada en dos secciones, la más larga de las cuales era a la sección más corta lo que toda la línea era a la sección más larga. Los matemáticos se entusiasmaron tanto con la belleza de este equilibrio de razones que, a mediados del Siglo XIX, empezaron a llamarlo «sección de oro».

Un rectángulo en el que la anchura y la longitud representasen una línea dividida por la sección de oro y doblada en ángulo recto en el punto de división fue llamado «rectángulo de oro».

Muchas personas creen que el rectángulo de oro representa una configuración ideal particularmente satisfactoria desde un punto de vista estético. Un rectángulo más largo —piensan— parece demasiado largo, y un rectángulo más corto, demasiado corto. Por tanto, la gente ha buscado (y encontrado) ejemplos de rectángulos de oro en pinturas, estatuas, edificios y muchos artefactos corrientes de nuestra sociedad. En libros populares de matemáticas se presentan al lector ilustraciones sobre esto.

Francamente, yo soy escéptico. Creo que la estética es un estudio muy complicado y que está enormemente influido por el medio social. Tratar de extraer mucho provecho de la sección de oro a tal respecto es demasiado simple. Por ejemplo, sólo tengo que ver películas realizadas en los años veinte y treinta para que me choque cómo han cambiado, en tan poco tiempo, nuestras ideas sobre la belleza femenina (que podríamos considerar, irreflexivamente, como eterna).

No niego que el rectángulo de oro es precisamente de oro por la elegancia matemática de la relación entre los lados, pero tratar de convertir esto en cuestión de estética es como dorar el oro refinado, y yo quisiera contribuir, con pobre aportación, a desdorarlo.

Si nos ceñimos estrictamente a las matemáticas, encontramos que la sección de oro puede hallarse en figuras geométricas tan simples como el decágono regular (figura simétrica de diez lados) y la estrella de cinco puntas (que encontramos en la bandera de los Estados Unidos). Particularmente interesante a este respecto es la serie de Fibonacci, de la que traté en un anterior ensayo de esta colección (véase «T-Formation», en Adding a Dimension, Doubleday, 1964). Allí sólo traté de algunos de los grandes números resultantes. Aquí desarrollaré otro aspecto.

La serie de Fibonacci empieza con dos 1 y genera entonces nuevos números, haciendo que cada nuevo número sea la suma de los dos anteriores.

Así, si empezamos la serie con 1, 1…, el tercer número es 1 + 1, o 2, y esto nos da 1, 1, 2… El número siguiente es 1 + 2, o sea, 3, y ahora tenemos 1, 1, 2, 3… Sigue 2 + 3, o sea, 5, de modo que tenemos 1, 2, 3, 5… Después viene 3 + 5 = 8, y 5 + 8 = 13, y así sucesivamente. Por tanto, las 21 primeras cifras de la serie de Fibonacci son: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2584, 4.181, 6.765, 10.946…

Si quisiéramos sumar pares de cifras cada vez más grandes, podríamos seguir añadiendo sumas adicionales indefinidamente, pero éstas 21 serán suficientes para nuestro fin.

Cuando se elaboró la serie de Fibonacci —por un matemático italiano llamado Leonardo Fibonacci (1170-1240)—, ésta tenía que ver con el crecimiento biológico. El problema inicial era, en realidad, la multiplicación de los conejos. Y, sin embargo…

Imaginemos que consideramos la razón de números sucesivos en la serie de Fibonacci, dividiendo cada número por el anterior y empezando con el segundo de la serie, así:

1/1 = 1

2/1 = 2

3/2 = 1,5

5/3 = 1,6666…

8/5 = 1,6

13/8 = 1,625

Como vemos, la razón forma una serie oscilante. El valor de la razón sube de 1 a 2, después baja a 1,5, luego sube a 1,6666…, luego baja a 1,6 y después a 1,625. Podemos asegurar que esto continuaría así, que la razón seguiría subiendo y bajando alternativamente, y así ocurre en realidad.

Sin embargo, la razón sube y baja en oscilaciones cada vez más pequeñas. Primero sube de 1 a 2, pero en ulteriores oscilaciones nunca vuelve a bajar hasta 1, ni a subir hasta 2. Entonces baja de 2 a 1,5, y todos los futuros valores están entre 1,5 y 2. Después sube a 1,6666…, y todos los valores futuros están entre 1,5 y 1,6666…

La oscilación es cada vez más pequeña, y, con cada nuevo paso, todos los valores futuros quedan atrapados entre las cada vez menores oscilaciones.

La oscilación nunca cesa del todo. Por mucho que prolonguemos la serie y por enormes que lleguen a ser los números, la razón continuará oscilando, aunque cada vez en menores cantidades. La oscilación, cada vez más pequeña, tendrá lugar a uno y otro lados de algún valor central, al que la razón se acercará cada vez más sin alcanzarlo nunca. Este valor central es el llamado «límite» de la serie.

¿Cuál es el limite de la serie de Fibonacci?

Continuemos la serie empezando con la última razón que hemos observado:

13/8 = 1,625

21/13 = 1,6153846…

34/21 = 1,6190476…

55/34 = 1,617647

89/55 = 1,6181818…

144/89 = 1,6179775…

233/144 = 1,6180555…

377/233 = 1,6180257…

610/377 = 1,6180371…

Esto empieza a parecer terriblemente sospechoso. Pasemos a las dos últimas razones en la serie de Fibonacci de 21 elementos que presenté anteriormente:

6765/4l81 = 1,618033963… y 10946/6765 = 1,618033998…

Las oscilaciones se están haciendo ciertamente muy pequeñas, y parecen oscilar alrededor del número que representa la sección de oro.

No, no es esto. Hay métodos matemáticos para determinar el límite de tales series, y se puede demostrar de modo concluyente que el límite de las razones de los términos sucesivos de una serie de Fibonacci es 1/2 (1 + ²R[ 5 ]).

Este hecho me encanta. Es un ejemplo de la belleza de lo inesperado que se puede encontrar en cualquier parte de las Matemáticas, si uno tiene talento para ello. Yo, por desgracia, no lo tengo.

NOTA del editor digital

«Raíz Cuadrada de» se representa en este ensayo como «²R[ ]» para evitar recargar con tipografía o gráficos el archivo».