7. El caso del hombre de negocios más rápido

ERAN las últimas horas de un sofocante día de agosto y yo caminaba cansadamente de regreso a casa a lo largo de la calle Marylebone. El apacible barrio de Notting Hill, donde viven muchos de mis pacientes, está separado de la calle Baker por unas zonas más desoladas y tuve que pasar con cuidado cerca de varios perros, tumbados en el suelo y con la lengua colgando mientras jadeaban, y de montones de basura podrida. Había tomado la imprudente decisión de hacer mi ronda de visitas a pie y, cuando por fin pude ver el número 221 B, la visión del sifón de soda y de la butaca se me apareció tentadoramente.

Sin embargo, la escena que me encontré en el vestíbulo fue mucho menos que agradable. La señora Hudson, de pie y con los brazos cruzados, le bloqueaba el paso a la escalera a un hombre alto, vestido con ropa cara y de algo más de mediana edad, que tenía una expresión irascible y con el que evidentemente ella había discutido. Me miró de manera casi suplicante.

—Doctor, acabo de entregarle la tarjeta de este caballero al señor Holmes y éste ha dejado muy claro que está muy ocupado y que no tiene tiempo para recibirle. Aun así este caballero dice que no aceptará un no por respuesta e incluso ahora mismo acaba de intentar empujarme para pasar. ¿Podría darle una explicación?

Me acerqué y me puse todo lo serio que me permitía ese calor sofocante.

—El señor Holmes es un hombre muy ocupado y tiene una gran clientela que quiere consultarle distintos asuntos —dije con frialdad—.

Yo soy su colega, el doctor Watson, y si fuese tan amable de explicarme su caso, quizás podría conseguirle una cita para los últimos días de la semana, o tal vez para la próxima. ¿A quién tengo el honor de dirigirme?

La cara del hombre se puso casi blanca por el enfado, y contrastaba de manera desagradable con el color rosa de su cuello.

—¡La semana que viene! —gritó con el duro acento del Bronx de Nueva York—. Por Dios, no es de extrañar que ustedes los británicos estén cayendo en un terrible declive mientras nosotros, los del otro lado del Atlántico, estamos creciendo con ímpetu. ¿No tiene conciencia del valor del tiempo? Mi nombre es Bamum Rolleman y soy uno de los hombres más poderosos de América. ¡Ahora dígale a su jefe que si no me recibe inmediatamente se arrepentirá de verdad!

Me puse más serio y le dije:

—Hablando como médico, debo advertirle que no se excite de este modo, ya que así provoca un esfuerzo poco aconsejable para su corazón. Puedo asegurarle que sus amenazas no le llevarán a ninguna parte y si desea que lleguemos a considerar su caso, le sugiero que…

Rolleman había estado temblando visiblemente por la rabia, pero ahora se había controlado y habló con un tono más moderado.

—No le estaba amenazando, caballero. Me refería al hecho de que yo soy un hombre adinerado y sé que siempre hay que pagar para conseguir el mejor consejo. Estoy siendo chantajeado de una manera que la policía no puede ayudarme. En lugar de pagar el chantaje quiero darle al detective privado que resuelva el caso una considerable suma… en realidad, una suma muy considerable. Estoy seguro de que el señor Holmes lamentará dejar pasar una oportunidad como ésta.

—Sé que Sherlock Holmes desaprueba especialmente el chantaje —dije—. Intentaré persuadirle para que le reciba, pero si lo que él establece es darle una cita para dentro de unos días, o incluso si decide no darle ninguna, usted tendrá que aceptarlo.

Asintió con desgana y yo subí por las escaleras hacia nuestras estancias. Sherlock Holmes estaba tumbado en el sofá vestido con una bata y haciendo ociosamente unos garabatos en una hoja de papel.

—Realmente Holmes —dije con severidad—, me resulta difícil creer que usted parezca el hombre más ocupado. Comprendo que la señora Hudson esté un poco enfadada por haber sido utilizada como vigilante de la puerta. ¿No tiene tiempo al menos para entrevistarse con este cliente acaudalado?

Movió una mano lánguidamente.

—En muy raras ocasiones los magnates de los negocios me proporcionan casos interesantes. Normalmente están involucrados en algún asunto financiero o de malversación sucedido en sus imperios que resulta ser una cuestión más apropiada para un contable que para un detective.

He sabido que Mycroft ha investigado casos de este tipo, pero sólo en nombre del gobierno. Él no malvende su talento y realmente a mí no me resulta estimulante analizar columnas y columnas de cifras y números por encargo de personas que ya poseen más riqueza de la que posiblemente tengan ocasión de gastar.

—Sus suposiciones son erróneas, Holmes —dije—. Rolleman está siendo chantajeado. Ni siquiera usted puede sacar apresuradas conclusiones sin molestarse en examinar el caso. Está en su perfecto derecho de rechazar el caso, pero realmente creo que podría hacerlo en persona en lugar de forzar a su casera a que actúe como intermediaria.

Había hablado con bastante firmeza y Holmes me miró y contestó suspirando:

—Muy bien, doctor. Si tengo que sacrificar algunos momentos para que luego haya paz y tranquilidad, que así sea. Haga entrar al señor Rolleman.

Salí hacia el rellano antes de que pudiese cambiar de opinión y desde arriba le hice una seña a Rolleman, que estaba paseando arriba y abajo por el vestíbulo. Subió corriendo las escaleras y sólo se detuvo cuando había subido todos los peldaños, a pesar de que evidentemente le costaba respirar. Entramos y vi que Holmes no se había preocupado de enderezar su postura. Con pereza señaló una silla.

—Señor Rolleman, me siento muy honrado —dijo con un tono ligeramente irónico—. ¡Pensar que un hombre que tiene tantos millones pueda visitar nuestra humilde morada. ¿Podría decirme cómo puedo ayudarle?

Nuestro huésped le miró con disgusto.

—Bueno, es fácil comprender por qué yo soy un hombre rico mientras que usted, a pesar de su ingenio, se halla en una situación bastante regular —afirmó—. No es la inteligencia lo que conquista el mundo, señor Holmes, sino la energía. La energía y, por encima de todo, la rapidez a la hora de actuar, ése es el secreto para el éxito y la riqueza. Haga las cosas rápido en lugar de mejor y ganará.

Sherlock Holmes levantó una ceja.

—Personalmente prefiero pensar que los avances humanos dependen más de la desidia —señaló—. Piense en el inventor de la rueda, por ejemplo. Apostaría a que no era una persona dinámica y ambiciosa, sino que simplemente detestaba el esfuerzo de tener que llevar sobre sus hombros a los animales que había cazado hasta su cueva. «Si evitase este pesado trabajo podría disfrutar de más tiempo para el ocio», debió pensar. Y así se inventó el carro.

Luego vino el hombre demasiado perezoso para perseguir rápidamente a su presa. «Si tuviese un medio para poder tirar mi lanza de manera que fuese más rápida que mi víctima», debió razonar sin ninguna duda, «me podría relajar y engordar mientras los demás corren desesperadamente por los alrededores». Y así se inventaron el arco y la flecha. Más adelante…

Realmente no pude culpar al señor Rolleman por interrumpirle, ya que parecía que Holmes estuviese dispuesto a recitar hasta el final esa curiosa interpretación de los muchos miles de años de la historia de la humanidad, a menos que se le parase a la fuerza.

—Su ejemplo sobre la invención de la flecha para mejorar la velocidad de la lanza resulta muy adecuado para mi caso, señor Holmes, ya que todo mi imperio está construido justamente gracias a la ventaja y los beneficios que entraña mejorar la rapidez. Comprobé que los buques de vapor con rueda de paletas irían más rápido que los veleros y que, por tanto, podría transportar mis mercancías más rápido que los demás, y así hice mi primera fortuna. Luego consulté a los mejores científicos e ingenieros y me dijeron que, a su debido tiempo, el propulsor de hélices superaría a la rueda de paletas, y así hice la segunda. Así mismo, utilicé el ferrocarril de vapor para llevar mis mercancías al interior del país mientras que los demás confiaron en el caballo y las carretas, y mi imperio creció por toda América.

Más recientemente descubrí que la capacidad del telégrafo para enviar mensajes instantáneamente podría resultar vital para anticiparse a la competencia. Convencí a los comerciantes de los grandes mercados de que podíamos hacer los negocios al instante gracias a la electricidad. Eso me proporcionó aún más dinero, pero también una amenaza. Y por eso he venido a verle.

Sherlock Holmes parecía ligeramente intrigado.

—Sí, antes mencionó un chantaje —dijo—. Por favor, continúe.

—Actualmente, mi negocio más provechoso es el Mercado Superior, cuya base está en Chicago. Es un barco en el que se compra y se vende y que permite a la gente de Mercado de Provisiones, empresa que está aquí en Londres, depositar sus ofertas para que todo resulte más cómodo. De algún modo, es muy similar a una casa de subastas.

Para la integridad del negocio resulta vital que todos los ofertantes potenciales reciban la información al mismo tiempo, ya que así se asegura la imparcialidad. Una vez que la han recibido, se aceptan las ofertas, sobre la base de que si hay dos iguales, como ocurre muy a menudo, gana la que se haya recibido primero.

El sistema de telégrafos se demostró inadecuado para nuestros propósitos, de modo que para aseguramos de que todos nuestros compradores europeos reciben la información exactamente al mismo tiempo, utilizamos una versión específicamente adaptada del aparato de Marconi recientemente perfeccionado. Desde Chicago se envía una señal al espacio para anunciar que se abren las ofertas y, puesto que esa señal viaja a la velocidad de la luz, es recibida en Londres justo 1/6 de segundo después. Los comerciantes que desean efectuar una oferta en ese momento envían inmediatamente una respuesta utilizando el mismo sistema. Cada ofertante tiene asignada una frecuencia de radio distinta.

Por supuesto, entre las empresas de correduría de Londres existe una intensa competitividad por comunicar sus ofertas lo más rápido posible. Hace unos meses dejaron de confiar en los operadores humanos para llevar a cabo esa tarea y ahora, cuando llega un aviso desde Chicago y desean comunicar su oferta, sólo tienen que apretar una tecla para que la respuesta sea enviada automática e instantáneamente. En Chicago, un aparato eléctrico puede distinguir cuál es la primera respuesta recibida, incluso si dos de ellas llegan con una diferencia de una millonésima de segundo o menos, y una bombilla eléctrica se ilumina para mostrar la identidad del ofertante ganador.

—¡Qué ingenioso, esos hombres ricos pueden jugar a una especie de póquer con mercancías de una manera muy rápida! —dijo Holmes moviendo la cabeza.

Rolleman le ignoró.

—Ya desde el principio me sentí muy preocupado de que pudiese haber alguna forma de engañar a este sistema —señaló—. Suponga que algún comerciante fuese capaz de anticipar la señal de radio procedente de Chicago; en ese caso podría ofertar antes que los demás. Imagine, por ejemplo, que algún cómplice americano tuviese cerca de Chicago un receptor de radio conectado a uno de los cables transatlánticos que sirven para transmitir los telegramas. El cómplice podría utilizar una clave telegráfica y mandar una señal a Londres que podría llegar allí antes que la onda de radio, al menos eso es lo que creo.

En cualquier caso, los más expertos científicos de América me aseguraron que ese tipo de cosas era imposible. Ninguna señal eléctrica, ni a través de un cable ni por el espacio, parece capaz de viajar más rápido que la luz. Así pues, no sería posible llevar a cabo un fraude de este tipo, al menos en principio.

Hasta hace pocas semanas, mi seguridad en la integridad del sistema era total, pero entonces recibí la siguiente carta, que llegó a Chicago con un sello de Londres.

Se la entregó a Sherlock Holmes y éste la leyó en voz alta:

«Estimado caballero:

Me complace informarle que he descubierto un sencillo método para transmitir mensajes a una velocidad más rápida que la de la luz. Puesto que soy una persona responsable, deseo evitar la desorganización en la seguridad del negocio, especialmente en lo que se refiere a su correduría, que podría provocar la publicación de este método.

En cualquier caso, espero una razonable compensación por renunciar a los ingresos que, de lo contrario, podría proporcionarme mi invento. Por favor, indique su conformidad a este trato poniendo el mensaje «Se Busca a Mandrágora» en la sección de Anuncios Personales del Times.

Atentamente, etc.

Mandrágora»

Sherlock Holmes levantó la vista.

—¿Es esta nota a lo que usted se refiere como chantaje?

—Así es.

—Bueno, a mí me resulta difícil llamarlo chantaje en sentido legal. Vender un invento, o incluso ocultar uno, es tan legal como sus propias actividades de negocios. ¿Por qué simplemente no hace una oferta para comprar ese aparato de Mandrágora?

Rolleman movió la cabeza y dijo:

—Ya me he puesto en contacto con él. Hemos intercambiado bastantes mensajes, pero él se niega a venderlo y sólo está dispuesto a mantener en secreto su invento sin dar ningún detalle, a excepción de unas indicaciones que me resultan incomprensibles.

—Bueno, seguramente debería considerar que está tratando de engañarle y que ¡ya es hora de desenmascararle! —dije.

—No me atrevo a hacer eso. Tengo entendido que han circulado ciertos rumores por Londres sobre unos nuevos descubrimientos referentes a la velocidad de la luz y sobre ciertos fenómenos relacionados con ella…

—Estamos informados de ello —comentó Holmes.

—Y si Mandrágora saliese a la luz, por mucho que sus peticiones fuesen infundadas, podría ser la ruina para mí correduría. Sin embargo, no estoy dispuesto a pagarle la suma que ha pedido sobre todo porque, como usted bien ha dicho, lo más probable es que sólo esté tratando de engañarme.

Lo que necesito, caballero, es una de estas dos cosas: o la información de que es posible enviar una señal a una velocidad más rápida que la de la luz, con alguna indicación sobre cómo se podría efectuar esa proeza, o bien una garantía de que eso es definitivamente imposible y de que lo será para siempre.

Holmes levantó las cejas.

—¿No ha podido encontrar a ningún científico dispuesto a proporcionarle esa información?

Rolleman se rió salvajemente.

—Me hubiese resultado fácil encontrarlo, pero yo tengo mi propio y particular modo de pagar por este tipo de opiniones.

Me gusta pensar que no soy muy tonto en los asuntos de negocios. Hace muchos años descubrí que el mundo está lleno de consejeros de todo tipo —abogados, científicos, contables— dispuestos a dar fáciles consejos que al final resultan ser castillos en el aire. Yo encontré una sencilla solución. En la actualidad pago por un consejo, pero no en forma de honorarios, sino de apuesta.

Sacó un talonario de cheques y una pluma estilográfica de su bolsillo y escribió en uno de ellos. Luego levantó ese cheque para que lo viésemos.

—Esto es un pagaré por valor de veinte mil libras a nombre del señor Sherlock Holmes.

No pude evitar resoplar.

—Pero sólo se lo entregaré a cambio de una apuesta firmada. Puede apostar que me podrá decir un método de enviar un mensaje a una velocidad más rápida que la de la luz o bien que una hazaña de este tipo es absolutamente imposible. La cláusula adicional es que si se puede demostrar que usted está equivocado, no sólo tendrá que devolverme mis veinte mil libras, sino que, como perdedor de la apuesta, deberá entregarme una suma igual.

He consultado a numerosos científicos y aunque ellos creen que es algo irreal poder enviar una señal más rápido que la luz, no encontré a ninguno que quisiera aceptar mi apuesta.

Holmes parecía divertirse.

—Yo podría aceptarla, señor Rolleman, pero necesitaré tiempo para pensarlo bien. ¿Está alojado en algún hotel? ¿El Savoy? Bien: le llamaremos mañana. Watson, sea tan amable de acompañar al señor Rolleman hasta la puerta.

Volví con Holmes algo alarmado.

—¡No puede estar pensando seriamente en aceptar su apuesta! —exclamé—. Le arruinaría si perdiese. ¡Qué manera tan perversa de pagar por un consejo!

—Al contrario, creo que es un modo bastante razonable. ¡Imagine qué rápidamente se libraría el mundo de falsos abogados y de contables incompetentes si todas las consultas se realizaran con estas condiciones! Pero no tenga miedo, Watson, no me precipitaré en este caso. Puedo pedir algunos favores que me deben y obtener consejo sobre este tema de tres de los hombres más inteligentes de Londres. Si no le importa, espéreme mientras me visto.

Mientras esperaba, reflexioné sobre la cuestión. Demostrar una negación resulta siempre problemático: al menos estaba seguro de que era algo bastante alejado de mis posibilidades. Pero encontrar un modo de enviar un mensaje a una velocidad más rápida que la de la luz me parecía un obstáculo aún más difícil. ¿No podría yo inventar algún dispositivo con espejos y lámparas que resolviese el problema?

Recibí la aparición de mi amigo con entusiasmo triunfante.

—No se moleste en ponerse el sombrero y los guantes, Holmes. No es necesario que salgamos fuera. Ya he resuelto el enigma.

Le mostré el diagrama que he reproducido más abajo y en el que había procurado emular el claro estilo de dibujo de Mycroft.

—La torre central representa un faro, Holmes. Bien, un marinero tiene la impresión de que un faro lanza su luz a intervalos regulares, pero, en realidad, emite un rayo estrecho de luz que gira debido a que una lente o un espejo de enfocar va dando vueltas alrededor de la lámpara central. En el instante que aparece en el dibujo, el rayo es emitido hacia el oeste. Suponga que el faro está emitiendo un destello por segundo, es decir, que el rayo de luz está girando a esa velocidad.

 

El faro del doctor Watson

 

Imaginemos que el faro está rodeado por una pared circular de poca altura que se halla a una distancia de un kilómetro. La longitud total de la pared es de unos seis kilómetros y el punto de luz se mueve a lo largo de ella a seis kilómetros por segundo. Por tanto, se está moviendo más deprisa que el casquillo más rápido que puede disparar un arma.

Ahora ampliamos el radio de la pared hasta mil kilómetros. El rayo de luz se desplaza a seis mil kilómetros por segundo. Y si aumentamos el radio hasta cien mil kilómetros, el punto de luz se mueve a seiscientos mil kilómetros por segundo… ¡esto es, el doble de la velocidad de la luz!

Sherlock Holmes frunció el ceño.

—Su diagrama es un poco engañoso, Watson. La razón es que se ha olvidado del hecho fundamental: la luz viaja a una velocidad finita. Si se pudiese ver la zona iluminada desde un punto muy elevado, se comprobaría que, en realidad, tiene la forma de una espiral. Bastante similar al chorro de agua que sale de un aspersor que gira para regar el césped de un jardín.

Dicho esto dibujó el diagrama que aparece abajo.

 

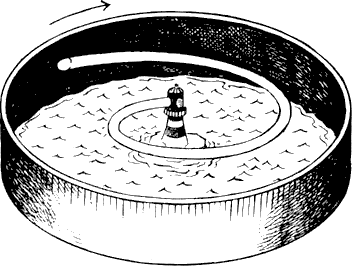
El faro de Sherlock Holmes

 

—A pesar de todo —insistí—, el punto de luz se sigue moviendo a lo largo de la pared al doble de la velocidad que la luz, o, en realidad, a la velocidad que yo quiera si la pared está lo suficientemente distante.

—Ah, pero necesitamos utilizarla para mandar una señal. ¿Cómo usaría el rayo de luz para enviar un mensaje desde un punto de la pared a otro?

—Bueno, supongo que una persona que se halle en la pared podría reflejar el rayo con un espejo de manera que vuelva hacia el faro… —sugerí, pero me detuve enseguida ya que me di cuenta de que había una objeción.

—Así es, Watson: su mensaje siempre tardará más tiempo, o como mucho la misma fracción de tiempo, que cuando se utiliza directamente la luz para transmitirlo.

Me negué a rendirme.

—No obstante, tengo aquí otro esquema que no depende para nada de las propiedades de la luz —dije mientras dibujaba el diagrama que aparece más abajo—. Esto representa un par de tijeras, Holmes. Un par de tijeras muy largas dignas de los experimentos mentales de Mycroft.

Piense en el punto de intersección cuando las hojas se cruzan. Está claro que ese punto se puede mover mucho más rápido que las propias hojas, dependiendo de la estrechez del ángulo que haya entre ellas. Por tanto, las hojas pueden moverse más lentamente que la luz y, sin embargo, el punto de intersección puede hacerlo más rápido.

 

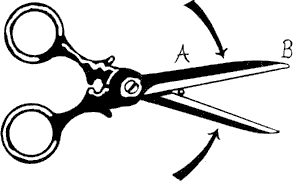
Las tijeras más rápidas que la luz

 

Holmes consideró la cuestión y preguntó:

—¿Y cómo utilizará ese efecto para enviar un mensaje?

—Del siguiente modo. Coloco en A un objeto pequeño y duro que sirva de bloqueo, de tal modo que llegaría a romper un par de tijeras reales. Las tijeras se cierran libremente hasta que las hojas llegan a A, luego se bloquean. Casi inmediatamente B recibe el efecto de ese bloqueo: por tanto, se puede enviar una señal.

—Un intento muy osado, Watson, pero me temo que sigue habiendo un problema. Las sustancias reales no son infinitamente duras ni rígidas. Si, por ejemplo, se golpea con fuerza el extremo de una regla, el otro extremo no se mueve instantáneamente, sino una fracción de segundo más tarde. De hecho, las vibraciones se desplazan a través de los objetos sólidos a unas velocidades determinadas, igual que el sonido se desplaza a través del aire a una velocidad concreta. Para las sustancias más duras y resistentes que se conocen, la velocidad es unas diez veces más rápida que la del sonido cuando viaja por el aire.

Y aun así es cien mil veces más lenta que la velocidad de la luz. Por consiguiente, los efectos de cualquier impacto que se produzca en A no serán transmitidos a B hasta después de un determinado tiempo. Sherlock Holmes me dio una palmada en el hombro y dijo:

—¡Bien pensado, a pesar de todo! Pero creo que éste es un problema para los expertos. Comentémoslo con otras personas. Llamemos en primer lugar al profesor Summerlee para ver qué piensa.

Holmes me condujo con rapidez a lo largo de Euston Street y luego atravesamos una entrada lateral del Colegio Universitario, rodeado por altos muros de piedra gris. Evidentemente era el patio destinado a la facultad de ciencias. Me detuve bajo un arco de piedra que tenía una inscripción griega sobre él.

—“No se permite la entrada a nadie que no sea apto para las matemáticas” —traduje.

—Esa era, supuestamente, la inscripción que había sobre la puerta de la escuela de lógica de Platón hace unos dos mil años —dijo Holmes—, En aquella época las matemáticas eran una disciplina rudimentaria. Alguien como usted, que puede realizar sumas o divisiones y que, incluso conoce la mística fórmula de Pitágoras, no sólo hubiese aprobado, sino que habría impresionado mucho a los encargados.

—Aun así, me siento como un hereje entrando en una catedral: ¡La piedra básica puede caer y aplastarme por impostor! —dije en broma.

En ese mismo instante se oyó un traqueteo de ruedas pasando sobre un pavimento empedrado y una puerta lateral se abrió para permitirle el paso a una carretilla cargada de pasteles al homo que, sin duda, estaban destinados a la despensa de la universidad.

—Por aquí —gritó Sherlock, y esquivamos a toda prisa al sorprendido mozo de carga para luego cruzar un corredor.

Odiaría ser responsable de su prematura defunción, Watson, y, en cualquier caso, la oficina de Summerlee se halla por este lado.

Instantes después, llamamos y entramos en una pequeña habitación completamente vacía. Tres paredes estaban cubiertas por unas pizarras garabateadas con símbolos y ecuaciones incomprensibles. Summerlee escuchó con impaciencia nuestra demanda de consejo.

—Es definitivamente imposible viajar más rápido que la luz —dijo enérgicamente—. ¿Recuerdan las fórmulas de la contracción relativista del tiempo y del espacio?

Señaló hacia una de las pizarras y vi que en ella se hallaban reproducidas las fórmulas de Mycroft (ver pág. 180).

—Una velocidad más rápida que la de la luz implica un Beta mayor de uno —dijo—. Y eso produce un factor para la contracción del espacio y del tiempo que sería la raíz cuadrada de un número negativo.

—Pero yo creía que el menos uno, o, en realidad, cualquier número negativo, no tenía raíz cuadrada —comenté.

—No una raíz cuadrada real —replicó Summerlee—. Un número negativo real multiplicado por otro número negativo real produce un resultado positivo, como desde luego sucede si se multiplican dos números positivos. Así que ningún número, ya sea positivo o negativo, produce un resultado negativo si es elevado al cuadrado. Sin embargo, podemos definir una cantidad imaginaria cuyo cuadrado es negativo, aunque es una invención matemática.

Puesto que está claro que las fórmulas dan resultados que no pueden pertenecer al mundo real, la consecuencia es que resulta completamente imposible que algo pueda hallarse en un sistema de referencia más rápido que la luz.

—No veo cómo… —intenté decir.

—Posiblemente no, pero ésa es la rigurosa respuesta matemática a su pregunta. Y ahora, aunque no deseo ser descortés, me temo que me aguardan algunas tareas más importantes que la resolución de una apuesta.

 

 

 

Media hora más tarde, después de dar un paseo por Hyde Park, nos hallábamos en los alrededores más despejados del Imperial College, donde nos condujeron hasta el despacho del profesor Challenger. Cuando llegamos junto a la puerta de roble, que estaba cerrada, oímos cómo retumbaba la airada voz del profesor. Parecía estar reprendiendo a algún desafortunado alumno. Al fin se abrió la puerta y apareció un hombre joven.

—¿Está libre el profesor Challenger? —preguntó Holmes.

—¿Desean verle? —preguntó a su vez el joven con algo de incredulidad; luego, tranquilizándose un poco, asintió con la cabeza y se marchó deprisa. Entramos en la guarida del profesor con un poco de nerviosismo, al menos por mi parte, y Sherlock le explicó la apuesta, así como la respuesta que nos había dado Summerlee.

Challenger se acomodó en su silla y se rió de buena gana.

—Una auténtica respuesta matemática —gritó con entusiasmo cuando fue capaz de hablar—. Es verdad que su respuesta puede implicar que es imposible viajar a una velocidad más rápida que la luz, pero realmente no es una eficaz exposición de por qué es imposible, o de qué pasaría si alguien lo intentase. A muchas pruebas matemáticas les pasa lo mismo. Pueden ser rigurosamente válidas, pero no ofrecen una clara explicación de la situación que describen.

Conozco una historia apócrifa sobre un estudiante de matemáticas que, para que ampliase su perspectiva científica, fue asignado a un proyecto geográfico. Le pidieron que determinase a través de una investigación si un lugar determinado estaba en una isla o en tierras del continente.

Realmente, caminó por todo el territorio continental arrastrando los pies y mirándose siempre los cordones de los zapatos. Tanto es así que había un túnel cavado para conectar la isla con el continente y, por casualidad, entró en él. Nunca se dio cuenta de que estaba en un túnel, aunque tampoco habría pensado que eso era importante en caso de que se hubiera apercibido de ello. Poco después se encontró accidentalmente con el lugar que andaba buscando. Puesto que había llegado hasta allí caminando por tierra firme, informó de que se hallaba en territorio continental.

Y en cierto sentido tenía razón. A un matemático sólo se le puede preguntar por una isla si se le proporciona una rigurosa definición de lo que es una isla, y lo mismo vale para cualquier otro tema. ¡Y según algunas definiciones, si se instala un túnel o un puente para conectar a la tierra firme con una isla, ésta deja de serlo! Pero su respuesta fue de poco provecho y, desde luego, él no había aprendido nada útil acerca del mundo que le rodea.

Así que enfoquemos su problema de una manera más práctica. Supongamos que un ingeniero desea disparar un proyectil a una velocidad más rápida que la de la luz. Los mejores cañones navales pueden disparar la munición aproximadamente a un kilómetro por segundo. Pero si montásemos un cañón de ese tipo sobre un vehículo que pudiese viajar a una velocidad cercana a la de la luz, ¿podríamos sobrepasar la velocidad de su trayectoria?

Imagine que el hipotético tren de su hermano Mycroft está moviéndose a 6/10 de la velocidad de la luz y que tiene un cañón de ese tipo apuntando hacia delante. Dispara. Desde el punto de vista de un observador situado junto a la línea férrea, ¿a qué velocidad viaja el proyectil?

De pronto se me hizo la luz.

—¡Ahá! —dije—. Desde la perspectiva de alguien que se halla junto a los raíles, el tren se comprime en función de la dirección en la que se desplaza y, además, el tiempo, a bordo del tren, discurre a un ritmo más lento según un factor que recuerdo bien: 4/5 de lo normal en cada caso. Si multiplicamos estos efectos, el proyectil sólo viajará seiscientos cuarenta metros por segundo más rápido que el tren.

Challenger se dirigió a mí.

—¡Muy bien! Pero nuestro ingeniero es persistente y aumenta la velocidad del tren justo hasta trescientos metros por segundo por debajo de la velocidad de la luz, es decir, una milésima parte menos, y dispara el cañón. ¿Qué resultado obtendría?

Vi las fórmulas de la contracción relativista del espacio y del tiempo en una pizarra próxima, la que aparece dibujada en la página siguiente.

—Bueno, los hechos que ocurran a bordo del tren parecerán que se desarrollan a paso de tortuga y, por añadidura, ¡el cañón y el proyectil serán aplastados hasta quedar con el grosor de un pelo!

—Así es. El proyectil apenas se arrastraría hacia delante y, ciertamente, no superaría la velocidad de la luz. De hecho, el método que se utiliza para aumentar las velocidades sólo es válido cuando una de esas velocidades es pequeña si se compara con la de la luz. Pero es sencillo idear una fórmula más precisa.

Escribió la última línea que aparece en la pizarra y prosiguió con su explicación.

—Sean lo grandes que sean las Betas iniciales, siempre y cuando todas sean menores que la unidad, la suma será también menor que la unidad.

Entonces alzó uno de sus dedos regordetes.

—Sin duda se estarán preguntando a dónde va a parar la energía de la pólvora utilizada. La respuesta es que es transmitida al proyectil. En un mundo relativista, la energía no es realmente proporcional al cuadrado de la velocidad, sino que aumenta exponencialmente a medida que nos acercamos a la velocidad de la luz.

Para propulsar el proyectil, o cualquier otro objeto, hasta la velocidad de la luz, se necesitaría una infinita cantidad de energía. Me atrevería a decir que esto es algo que impone un límite fundamental a los esfuerzos de nuestro ingeniero.

 

Las ecuaciones relativistas

 

Pensé en la novela de Wells, El primer hombre en la Luna, que hacía poco que había terminado. Había estado leyendo que las estrellas estaban mucho más lejos que la Luna y me había preguntado si alguna vez podríamos viajar hasta ellas.

—Se cree que la estrella más cercana a nuestro Sol está tan lejos que su luz tarda cinco años en llegar hasta nosotros —expliqué—. Me está diciendo que yo nunca podría llegar hasta allí en menos de cinco años, aunque fuese a bordo de la aeronave más prodigiosa.

Challenger sonrió graciosamente.

—Desde su perspectiva, sí que podría —dijo—. A medida que acelerase, vería como si el propio Universo se estrechase en la dirección de su vuelo, de modo que, aunque usted nunca tendría la sensación de que está viajando más rápido que la luz, sí que podría efectivamente llegar allí en un tiempo más corto.

—¡Sería como si el mismo espacio se estuviese curvando!

—No exactamente curvándose, mi querido doctor, sino comprimiéndose a sí mismo de manera constante. Esa sería una descripción más precisa.

Sherlock Holmes asintió inclinando la cabeza.

—Sin embargo, para un observador que estuviese aquí en la Tierra, ese viaje de ida y vuelta tardaría al menos diez años en concluirse, y ésa es la cuestión más relevante para nuestra apuesta. Puedo aceptar sin problemas que ningún objeto físico puede viajar por encima de la velocidad de la luz, pero estoy menos seguro en lo que se refiere a otras manifestaciones. Profesor, ¿puede decirme con certeza que no se podría descubrir ningún nuevo tipo de radiación, o de cualquier otra cosa, que se pudiese transmitir a una velocidad más rápida que la de la luz?

Challenger reflexionó durante unos instantes.

—No, no puedo ser tan concluyente —contestó al final de mala gana—. Un hombre sabio nunca asume que lo que todavía no se puede realizar es imposible para siempre, ya que conoce los límites de sus propios conocimientos. ¿Quién sabe lo que se puede descubrir mañana? Posiblemente no podría garantizar una cosa de este tipo.

—Me temo que estamos metidos en una búsqueda absurda, Watson —dijo Holmes mientras abandonábamos el Colegio; luego le echó un vistazo a su reloj—, Pero se acerca la hora del cóctel y, seguramente, Mycroft estará en su club, que está de camino a casa. Entraremos un momento para consultarle, aunque estoy seguro que será de la misma opinión que Challenger.

Sin embargo, por una vez, Holmes estaba equivocado. Mycroft nos miró con gran interés mientras le explicábamos el problema.

—Les puedo decir casi definitivamente que es imposible enviar por cualquier medio una señal a una velocidad más rápida que la de la luz —dijo—. Usted es un gran admirador de Wells, doctor. ¿Ha leído La máquina del tiempo? Le gustó, pero ¿considera que es posible?

Estuve a punto de reírme sonoramente, pero justo antes me acordé de que eso constituiría una grave violación de la etiqueta en el Club Diógenes, incluso en la Sala de Invitados.

—Una divertida fantasía, pero obviamente es imposible —dije—. Bueno, si pudiese viajar hacia atrás en el tiempo, podría volver y matar a mi abuela antes de que tuviese hijos, así yo no estaría aquí hoy. ¡Volver atrás y cometer la ejecución! O podría mandarme un mensaje que supiese que no he recibido. Aunque fuese posible comunicarse hacia atrás en el tiempo, no se terminarían las paradojas.

Mycroft asintió inclinando la cabeza.

—Muy bien, doctor —dijo con énfasis—. Ahora consideren que mi tren imaginario, con el que ya están familiarizados, tiene una longitud correspondiente a un segundo de luz. Imaginemos que el conductor que se encuentra en la parte delantera y el vigilante que se halla en la parte trasera se pueden comunicar a través de algún tipo de supertelégrafo. Normalmente, una señal debería tardar al menos un segundo en recorrer la distancia que hay entre los dos, pero supondremos que este telégrafo funciona instantáneamente.

A continuación, situamos a dos hombres junto a la línea férrea, separados de modo que, desde su perspectiva, la locomotora del tren se encuentre a la misma altura que el primero de ellos justo cuando el vagón del vigilante esté a la altura del segundo. Estos dos hombres también se hallan comunicados por un supertelégrafo igual que el anterior.

 

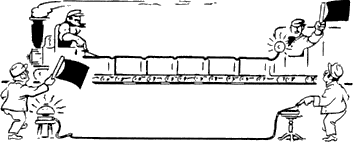
La señal llegando antes de que haya sido enviada

 

Ahora consideren la siguiente secuencia de acontecimientos. De los dos hombres que se encuentran junto a los raíles, el que está más adelantado le hace una señal al conductor cuando éste pasa junto a él. El conductor transmite la señal al vigilante.

Ahí está el quid de la cuestión. No olviden que mientras que desde el punto de vista del conductor y del vigilante, los dos hechos, es decir, la emisión y la recepción del mensaje entre conductor y vigilante, se producen simultáneamente, para los observadores que se hallan junto a la línea férrea, el acto del vigilante se produce antes que el del conductor. La princesa murió antes que el príncipe. Por tanto, desde el punto de vista de quienes están junto a los raíles, ¡el vigilante recibe su mensaje más de un segundo antes de que haya sido enviado!

El vigilante envía una señal al observador más atrasado cuando pasa junto a él. El observador más atrasado le devuelve esa señal a su compañero más adelantado, es decir, el que la había enviado en primera instancia.

—Tendríamos que haber probado estos complicados y sutiles ejercicios de envíos de señales durante el tiempo que estuve en Afganistán —añadí—. Pasar un mensaje de un hombre a otro y luego, cuando llegase a su destino final, comprobar si había sido malinterpretado. Corría un rumor de que el mensaje “El enemigo avanza, envíen refuerzos” había sido interpretado como “La tía de Emilio ha muerto, envíen tres o cuatro peniques”.

Mycroft me miró con severidad.

—Bueno, hay algo aún más relevante en este asunto —dijo—. ¿No se dan cuenta? ¡La señal regresa al observador más adelantado más de un segundo antes de que haya sido enviada! Se ha producido pues una clara paradoja.

De hecho, es fácil comprender que, si fuese posible enviar una señal cualquiera incluso a una velocidad ligeramente superior a la de la luz, entonces con la ayuda de un tren lo suficientemente rápido —o en otras palabras, de un par de aparatos de envío de señales— se podría enviar a tiempo un mensaje de respuesta. Es una garantía tan segura como que ustedes podrían desear que una hazaña de este tipo resultara imposible para siempre.

 

 

 

Sherlock le dio las gracias y nos dirigimos hacia el hotel Savoy. Por mi cabeza pasaron visiones de riqueza. Mi amigo siempre había preferido dedicarse a casos interesantes en lugar de intentar resolver los más lucrativos. ¿En qué cambiarían sus costumbres con veinte mil libras?

Una conserje nos condujo hasta la suite del señor Rolleman y llamó a la puerta. No hubo respuesta.

—Seguro que está dentro —dijo—. Pasó junto a mí hace muy poco tiempo. Parecía indispuesto, como si le faltase el aire.

La chica abrió la puerta y enseguida se echó hacia atrás dando un grito. El señor Rolleman yacía casi a sus pies con los ojos en blanco y la cara espantosamente violeta. Me arrodillé y le examiné mientras Holmes recorría rápidamente la habitación buscando indicios de posibles intrusos.

—No tiene que resolver ningún caso, Holmes. Está claro que se trata de una gran apoplejía. Hoy mismo, hace algunas horas, vi los signos de la enfermedad: no tengo que haber sido el primer médico cuyos avisos de que se tomase las cosas con más calma haya ignorado.

—Cuántas veces se hace realidad ese viejo dicho tan manido: “A más prisa, menos velocidad”. Al menos a la larga —comentó Holmes mientras nos marchábamos.

En cierto sentido, el señor Rolleman tenía razón en lo que se refiere a su opinión sobre mí: según su manera de ver las cosas yo soy un aficionado, ya que aplico mis capacidades y mi talento en la investigación porque me gusta, a pesar de que ese mismo esfuerzo podría hacerme más rico si me dedicase a otra actividad. Yo vivo en un alojamiento modesto que muchos considerarían modesto porque me conviene, pero paso el tiempo confortablemente, de un modo que se adapta a mi forma de ser como un par de zapatillas usadas, con la cantidad justa y necesaria de excitación y aventura como condimento. Y puesto que, al fin y al cabo, a todos nos aguarda el mismo destino que al señor Rolleman, Watson, ¿a qué más puede aspirar cualquiera de nosotros, sino a vivir la vida a la velocidad más adecuada?