6

RAMANUJAN, EL MÍSTICO MATEMÁTICO

Mientras Hardy y Littlewood avanzaban fatigosamente a través del extraño espacio de Riemann, a cinco mil millas de distancia, en las oficinas de la capitanía del puerto de Madrás, en la India, un joven empleado llamado Srinivasa Ramanujan había desarrollado una obsesión por el misterio embriagador del flujo irregular de los números primos. En lugar de ocuparse del tedioso deber de mantener los registros contables, para lo que había sido contratado, pasaba su tiempo llenando cuadernos de observaciones y cálculos en búsqueda de lo que dictaba el ritmo a aquellos extraños números. Ramanujan contaba los números primos sin tener la menor noción de la sofisticada perspectiva que se había elaborado en Occidente. Carente de una instrucción formal, no tenía el respeto reverencial que mostraban Hardy y Littlewood hacia la teoría de los números y hacia los números primos en particular, que Hardy definía como «la más difícil de todas las ramas de las matemáticas puras». Desvinculado de toda tradición matemática, Ramanujan se sumergió en los números primos con un entusiasmo casi infantil. Su candor, combinado con una extraordinaria predisposición natural para las matemáticas, se reveló como su gran fuerza.

En Cambridge, Hardy y Littlewood estudiaban ávidamente la maravillosa historia de los números primos desarrollada en el libro de Landau; en la India, la obsesión de Ramanujan por los primos se había inspirado en un libro mucho más elemental, pero con consecuencias igualmente amplias. Hay algunos momentos decisivos en la vida de un joven científico que a veces pueden identificarse como fundamentales para su futuro desarrollo, para Riemann se trató del libro de Legendre que le dieron cuando era estudiante: aquel libro depositó la semilla que habría de germinar en una fase posterior de su vida. Para Hardy y Littlewood, el libro de Landau tuvo una influencia muy fuerte. En 1903, a los quince años, Ramanujan descubrió una copia de A synopsis of Elementary Results in Pure and Applied Mathematics de George Carr. Excepto por su relación con Ramanujan, el libro de Carr y la vida de su autor tienen escasa importancia, pero para Ramanujan fue importante la estructura del libro: era una lista de unos 4.400 resultados clásicos de las matemáticas; sólo resultados, sin demostraciones. Ramanujan aceptó el reto y dedicó los años siguientes a estudiar a fondo el libro y a explicar cada una de las afirmaciones que describía. Como tenía poca familiaridad con el estilo occidental de demostración, Ramanujan tuvo que crear sus propias matemáticas. El hecho de no estar atado por la camisa de fuerza de las formas convencionales de pensamiento le dio la libertad de moverse a placer, y no pasó mucho tiempo antes de que su libreta se llenara de ideas y resultados que no aparecían en el libro de Carr.

Euler se había devanado los sesos con muchas de las afirmaciones no demostradas de Fermat. En las aproximaciones de Ramanujan a los problemas matemáticos podemos reconocer el mismo espíritu de Euler: poseía una capacidad fantástica de intuir la manera de dar vueltas y más vueltas a las fórmulas hasta hacer emerger nuevas perspectivas. Sintió una gran emoción cuando descubrió por su cuenta la relación que los números imaginarios proporcionan entre la función exponencial y las ecuaciones que describen las ondas sonoras. Pero su alegría se transformó en desesperación cuando, pocos días después, el joven empleado indio descubrió que Euler se le había adelantado unos ciento cincuenta años. Humillado y desanimado, Ramanujan escondió sus cálculos en el desván de su casa.

La comprensión del significado de la creatividad matemática es, en el mejor de los casos, difícil, pero la forma de proceder de Ramanujan siempre tuvo algo de misterioso: afirmaba que la diosa Namagiri, protectora de su familia y consorte de Narashima, el dios león, cuarta encarnación de Vishnu, le aportaba sus ideas en sueños. En la aldea de Ramanujan algunos creían que la diosa tenía el poder de exorcizar los demonios; para Ramanujan, Namagiri era la explicación de los relámpagos de iluminación que desencadenaban su flujo ininterrumpido de descubrimientos matemáticos.

Ramanujan no es el único ejemplo de matemático para quien el mundo de los sueños resulta ser un territorio fértil para la exploración matemática. Dirichlet tenía las Disquisitiones arithmeticae bajo la almohada, esperando recibir la inspiración para comprender las afirmaciones a menudo crípticas que contenía el libro. En los sueños es como si la mente se liberara de las barreras del mundo real y tuviera la libertad de abrir caminos que se excluyen en estado consciente. Ramanujan parecía capaz de inducir este estado onírico en sus horas de vigilia: un trance así está muy cerca del estado mental que la mayoría de los matemáticos intenta conseguir.

Hadamard, que se hizo famoso demostrando el teorema de los números primos, estaba fascinado por lo que ocurre en la mente de un matemático creativo. Puso sus ideas por escrito en un libro titulado The Psychology of Invention in the Mathematical Field, que publicó en 1945, donde avanzaba poderosas tesis sobre el papel del subconsciente. Actualmente los neurólogos se interesan cada vez más por los mecanismos de la mente matemática, porque podrían ayudar a conocer el funcionamiento del cerebro. A menudo es en los períodos de reposo o de sueño donde se concede a nuestro cerebro la libertad de jugar con ideas que se han implantado en el cerebro durante una actividad intelectual consciente.

En su libro, Hadamard dividía el acto del descubrimiento matemático en cuatro etapas: preparación, incubación, iluminación y verificación. Si Ramanujan tenía un don natural para la tercera etapa, claramente le faltaba talento para la cuarta. La simple iluminación le bastaba, pero no consideraba la etapa de verificación. Quizás el hecho de no estar presionado por la responsabilidad de la demostración le concedía la libertad de descubrir nuevos caminos en el páramo matemático. Su estilo intuitivo contrastaba con las tradiciones científicas de Occidente; como escribió Littlewood más adelante: «de hecho no poseía una idea muy clara de lo que se entiende por demostración; si del conjunto de la mezcla de indicios y de intuiciones extraía una certeza, no iba más allá».

Las escuelas indias debían mucho a las ideas que había introducido el Imperio británico, sin embargo, el sistema didáctico inglés, que tan útil había sido para Hardy y Littlewood, no fue de ninguna ayuda para el joven Ramanujan en la India: en 1907, mientras la tesis doctoral de Littlewood recibía una calurosa acogida en Cambridge, Ramanujan suspendía por tercera y definitiva vez los exámenes de admisión en el College. Ciertamente, habría superado aquellos exámenes si sólo se hubiera tratado de matemáticas, pero se le pedían también conocimientos de inglés, de historia, de sánscrito e incluso de fisiología. Como buen brahmán, Ramanujan era rigurosamente vegetariano, y para él la disección de ranas y conejos era intolerable. Pero el fracaso, aunque significó que no podría ingresar en la Universidad de Madrás, no extinguió el fuego matemático que ardía en su interior.

En 1910, Ramanujan esperaba impacientemente que sus ideas recibieran alguna forma de reconocimiento; en particular, le interesaba una fórmula que parecía proporcionar una cuenta extraordinariamente precisa de los números primos. En un principio había experimentado la frustración que casi todos sufren al intentar domesticar esta salvaje secuencia de números, pero Ramanujan sabía hasta qué punto los números primos son fundamentales para las matemáticas, y no abandonó su convicción de la existencia de una fórmula capaz de explicarlos. Como comentó Littlewood más adelante: «¿qué gran matemático hubiera sido Ramanujan cien o ciento cincuenta años antes? ¿Qué habría ocurrido si hubiera entrado en contacto con Euler en el momento oportuno?… Pero el gran período de las fórmulas parece que ya ha pasado». Sin embargo, Ramanujan no había estado sometido al cambio de perspectiva que indujo Riemann: estaba decidido a hallar una fórmula que produjera los números primos, y estaba ansioso por explicar sus descubrimientos a cualquiera que pudiese apreciar sus ideas.

La impresión que producían sus cuadernos y la influencia de la red brahmánica le garantizaron un empleo de contable en la capitanía del puerto de Madrás. Incluso empezó a publicar sus ideas en el Journal of the Indian Mathematical Society, y su nombre había llamado la atención de las autoridades británicas. C. L. T. Griffith, que trabajaba en el Instituto de Ingeniería de Madrás, reconoció que la obra de Ramanujan era la de un «matemático notable», pero no se sentía capaz de comprenderla o de criticarla. En consecuencia, decidió pedir la opinión de uno de los profesores que le habían enseñado matemáticas cuando estudiaba en Londres.

Al faltarle una preparación formal, Ramanujan había elaborado un muy personal estilo matemático. Por ello no tiene nada de extraño que, cuando el profesor Hill del University College de Londres recibió las cartas en las que Ramanujan afirmaba haber demostrado que 1 + 2 + 3 + 4 + … + ∞ = −1/12, liquidó buena parte de ellas por tratarse de un sin sentido. Una fórmula así se presenta como ridícula incluso a un ojo no calificado: ¡sumar todos los números enteros y obtener como resultado una fracción negativa es claramente la obra de un loco! «El señor Ramanujan ha caído en las trampas del tema más bien difícil de las series divergentes», escribió el profesor a Griffith.

A pesar de todo, el juicio de Hill no fue totalmente negativo. Animado por esos comentarios, Ramanujan decidió tentar a la suerte y escribir directamente a algunos matemáticos de Cambridge. Dos de los destinatarios no consiguieron penetrar en el mensaje que se escondía detrás de la extraña matemática de Ramanujan y rechazaron su petición de ayuda. Pero luego la carta de Ramanujan fue a parar al escritorio de Hardy.

Las matemáticas parecen tener el poder de atraer a los excéntricos, y quizás una parte de la responsabilidad ha de atribuirse a Fermat. El modelo de carta de rechazo de Landau da testimonio de la cantidad de respuestas absurdas que se reciben procedentes de individuos que reivindican su derecho a recibir el premio Wolfskehl por haber resuelto el último teorema de Fermat. Los matemáticos están acostumbrados a recibir cartas no solicitadas llenas de locas teorías numerológicas; Hardy, por ejemplo, estaba acostumbrado a quedar sumergido en un diluvio de manuscritos cuyos autores, como recordaba su amigo C. P. Snow, afirmaban haber resuelto los misterios proféticos de la Gran Pirámide o descifrado los criptogramas que Francis Bacon había escondido en los dramas de Shakespeare.

Hacía poco que Ramanujan había recibido un ejemplar del libro de Hardy: Orders of Infinity, de parte de Ganapathy Iyer, un profesor de matemáticas de Madrás con quien pasaba veladas enteras en la playa discutiendo de matemáticas. Mientras leía a Hardy, Ramanujan debió de comprender que finalmente había encontrado a alguien capaz de apreciar sus ideas, pero más tarde reconoció haber temido que sus sumas infinitas indujeran a Hardy «a hacerme notar que mi destino era el manicomio». Había una afirmación de Hardy que interesaba particularmente a Ramanujan: «Hasta hoy no se ha encontrado una expresión definida que proporcione la cantidad de números primos menores que un número dado cualquiera». Ramanujan había descubierto una expresión que creía que daba tal número con una precisión casi absoluta, y ardía en deseos de saber lo que pensaría Hardy de su fórmula.

La primera impresión de Hardy, cuando encontró en el correo de la mañana el enorme sobre de Ramanujan cubierto de sellos indios, no fue favorable: dentro había un manuscrito lleno de teoremas extraños, delirantes, sobre la cuenta de los números primos, junto con resultados muy conocidos que se presentaban como descubrimientos originales. En la carta adjunta, Ramanujan declaraba que había «encontrado una función que da una representación exacta de la cantidad de primos». Hardy sabía que se trataba de una afirmación estupenda, pero en el manuscrito no aparecía ninguna fórmula; peor todavía: ¡no se demostraba nada! Para Hardy, la demostración lo era todo. Una vez, hablando con Bertrand Russell en el comedor del Trinity College, dijo: «Si yo consiguiera demostrar con la lógica que tú morirás dentro de cinco minutos, estaría consternado por tu muerte inminente, pero mi dolor quedaría muy mitigado por el placer de la demostración».

Según C. P. Snow, tras una ojeada al trabajo de Ramanujan, Hardy «no sólo se había aburrido, sino que también estaba irritado. Daba la impresión de tratarse de un curioso fraude». Pero antes del atardecer aquellos locos teoremas empezaron a ejercer su magia y Hardy convocó a Littlewood para discutirlos después de cenar. A medianoche estaban descifrados. Armados con los conocimientos necesarios para comprender el lenguaje no convencional de Ramanujan, ahora Hardy y Littlewood se daban cuenta de que no se trataba de las manifestaciones de un desequilibrado sino de la obra de un genio, de un matemático falto de preparación formal pero, sin la menor duda, brillante.

Ambos comprendieron que la suma infinita aparentemente insensata de Ramanujan no era otra cosa que el redescubrimiento del método para definir la parte que falta del paisaje zeta de Riemann. La clave para decodificar la fórmula de Ramanujan consiste en expresar el número 2 como 1/(2⁻¹) (2⁻¹ es otra forma de escribir 1/2). Aplicando el mismo truco a cada número de la suma infinita, Hardy y Littlewood reescribieron la fórmula de Ramanujan en la forma siguiente:

Lo que tenían delante era la solución de Riemann para el cálculo de la función zeta cuando se le introducía el número −1. Sin una instrucción formal, Ramanujan había recorrido todo el camino solo y había reconstruido el descubrimiento que Riemann había hecho del paisaje zeta.

La carta de Ramanujan no podía haber llegado en mejor momento: gracias al libro de Landau, Littlewood y Hardy estaban fascinados por las maravillas de la función zeta de Riemann y por sus conexiones con los números primos. Y he aquí que Ramanujan afirmaba tener una fórmula increíblemente precisa para calcular la cantidad de números primos que se hallan en un intervalo numérico dado. Aquella misma mañana, Hardy había descartado esta afirmación, convencido de que Ramanujan era uno de tantos desequilibrados que se dedican a las matemáticas. Pero su trabajo de la tarde había colocado aquel sobre procedente de la India bajo una luz completamente distinta.

Hardy y Littlewood debieron de quedar atónitos ante la afirmación de Ramanujan según la cual su fórmula permitía calcular la cantidad de números primos hasta 100.000.000, «en general sin ningún error y en algunos casos con un error de 1 o de 2». El problema radicaba en que no daba ninguna fórmula. En efecto, toda la carta era profundamente frustrante para los dos matemáticos, ya que para ellos era absolutamente fundamental disponer de una demostración. Las fórmulas y las afirmaciones que llenaban la carta, en cambio, nunca se justificaban ni se explicaba de dónde venían.

Hardy respondió a Ramanujan en términos muy positivos, pidiéndole que mandara las demostraciones y mayores detalles sobre las fórmulas relativas a los números primos. Littlewood añadió una nota pidiendo que les mandara la fórmula para los números primos y «todas las demostraciones posibles, rápidamente». Los dos matemáticos estaban en ascuas ante la respuesta de Ramanujan. Pasaron muchas cenas intentando descifrar otras partes de su primera carta. Bertrand Russell escribió a un amigo que había encontrado «durante la cena a Hardy y Littlewood en un estado de gran agitación, porque creían haber descubierto a un segundo Newton, un empleado hindú de Madrás con un estipendio de 20 libras al año».

Puntualmente llegó una segunda carta de Ramanujan. Contenía varias fórmulas para calcular la cantidad de números primos, pero faltaba todavía una demostración. «Qué exasperante su carta en estas circunstancias» escribió Littlewood, y conjeturó que quizá Ramanujan temía que Hardy tuviera la intención de robarle sus descubrimientos. Al estudiar esta segunda carta, Hardy y Littlewood descubrieron que Ramanujan había concebido otro de los descubrimientos fundamentales de Riemann: el perfeccionamiento de la fórmula de Gauss para la cuenta de los números primos que introdujo Riemann era muy preciso, y además Riemann había descubierto cómo usar los ceros del paisaje zeta para eliminar los errores que todavía daba su fórmula; literalmente de la nada, Ramanujan había reconstruido una parte de la fórmula que Riemann había ideado cincuenta años antes. La fórmula de Ramanujan incluía el perfeccionamiento de Riemann sobre la estimación del número de primos que Gauss había dado, pero no las correcciones que Riemann obtuvo utilizando los ceros de su paisaje.

¿Quizá Ramanujan estaba afirmando que los errores que producen los puntos a nivel del mar se anulaban de alguna manera milagrosa? Fourier había proporcionado una explicación musical de estos errores: cada cero es como un diapasón, y cuando vibran todos juntos estos diapasones crean el ruido de los números primos. Quizá las ondas sonoras pueden combinarse para producir el silencio si se anulan unas a otras. En un aeroplano se reduce el zumbido de los motores creando ondas sonoras en el interior de la cabina para compensarlo, ¿podía ser que Ramanujan estuviera afirmando que las ondas de los ceros de Riemann crearían silencio?

Durante las vacaciones de Pascua, Littlewood marchó a Cornualles con su amante y la familia de ésta acompañado de una copia de la carta de Ramanujan. «Estimado Hardy —escribió (nunca se llamaban el uno al otro por el nombre de pila)—, la cuestión de los números primos está equivocada». Littlewood había conseguido demostrar que en ningún caso los errores causados por aquellas ondas podrían anularse unos a otros para justificar lo que afirmaba Ramanujan, es decir, que su reconstrucción de la fórmula de Riemann no era tan precisa como él afirmaba. Siempre habría ruido, por más lejos que llegáramos a contar.

Ocurrió que el análisis de Littlewood, estimulado por la carta de Ramanujan, lo llevó a una nueva intuición interesante sobre la obra de Riemann. La hipótesis de Riemann era importante para los matemáticos porque implicaba que la diferencia entre la estimación de Gauss y la verdadera cantidad de números primos comprendidos entre 1 y N sería muy pequeña en relación con N; en realidad nunca habría sido mayor que la raíz cuadrada de N. Pero si se hubiera hallado un simple cero fuera de la recta mágica de Riemann, entonces el error sería mucho mayor. Ahora, la carta de Ramanujan parecía sugerir que era posible hacerlo mejor que Riemann: podía suceder que, al seguir contando números primos, el error resultara todavía menor que la raíz cuadrada de N. El trabajo de Littlewood en Cornualles truncó aquella esperanza: Littlewood consiguió demostrar que en un número infinito de casos el error producido por los ceros sería al menos tan grande como la raíz cuadrada de N. La hipótesis de Riemann representaba el escenario óptimo: sencillamente, Ramanujan se había equivocado, pero a pesar de ello Hardy había quedado impresionado. Como escribió más adelante: «no estoy seguro de que en cierto modo este fracaso no haya sido más maravilloso que todos sus triunfos».

«Tengo una vaga teoría sobre el origen de sus errores». En su carta a Hardy, Littlewood conjeturaba que Ramanujan creía erróneamente que en el paisaje zeta no había puntos a nivel del mar; si realmente hubiera sido así, entonces las fórmulas de Ramanujan hubieran resultado exactas. No obstante, Littlewood estaba emocionado: «Puedo creer que se trata al menos de un Jacobi», declaró, comparando a Ramanujan con una de las celebridades entre los matemáticos de la generación de Riemann. Hardy escribió a Ramanujan: «Haber demostrado lo que usted afirma habría sido la empresa matemática más extraordinaria de toda la historia de las matemáticas». Estaba claro que, a pesar de su enorme talento, Ramanujan tenía una desesperada necesidad de que lo pusieran al día sobre el estado actual de los conocimientos. Littlewood escribió a Hardy sobre su intuición: «No sorprende que haya terminado por equivocarse, ignorante como parece sobre la diabólica malignidad que esconden los primos». Como observó Hardy: «tenía un handicap imposible de superar, un hindú pobre y solitario que se medía intelectualmente con la sabiduría acumulada en Europa».

Decidieron hacer todo lo posible para traer a Ramanujan a Cambridge. Enviaron a la India a E. H. Neville, un profesor del Trinity College, para que convenciera a Ramanujan de la conveniencia de unirse a ellos. Al principio Ramanujan era reacio a dejar la India ya que, al ser un brahmán practicante, creía que cruzando los mares se convertiría en un paria. Un amigo, Narayana Iyer, se dio cuenta de las vacilaciones de Ramanujan y trazó un plan. Iyer estaba convencido de que la devoción de Ramanujan por las matemáticas y la que sentía por la diosa Namagiri podrían, reunidas, producir una revelación que lo persuadiera de la conveniencia de ir a Cambridge. Lo acompañó al templo de Namagiri para buscar la inspiración divina; al cabo de tres días durmiendo sobre el suelo de piedra del templo, Ramanujan se despertó con sobresalto y corrió a despertar a su amigo: «He visto en un relámpago de luz resplandeciente a Namagiri ordenándome que atravesara el mar». Iyer sonrió: su plan había funcionado.

Ramanujan también temía la oposición de su familia, pero Namagiri, la divinidad que lo protegía, intervino de nuevo: la madre de Ramanujan soñó que su hijo tomaba asiento en una gran sala rodeado de europeos y que la diosa Namagiri le ordenaba que no pusiera dificultades. Por último, le preocupaba la perspectiva de volver a someterse a exámenes humillantes cuando llegara a Cambridge. Neville consiguió disipar este último temor: todo estaba ya a punto para que Ramanujan cambiara la extensión caótica de casas minúsculas de Madrás por los imponentes salones y las grandes bibliotecas de Cambridge, el escenario soñado por su madre.

CHOQUE CULTURAL EN CAMBRIDGE

En 1914, Ramanujan llegó a Cambridge, y así pudo dar comienzo una de las grandes colaboraciones de la historia de las matemáticas. Hardy habló siempre con pasión del período de colaboración con Ramanujan: cada uno gozaba con las ideas del otro, encantados de haber hallado un espíritu afín con quien compartir su amor por los números. Más adelante Hardy evocaría aquellos años como unos de los más felices de su vida y hablaría de su relación con Ramanujan en términos conmovedores, definiéndola como «la única historia romántica de mi vida».

La asociación de Hardy y Ramanujan recuerda a la clásica pareja de policías que dirige un interrogatorio, una pareja con un bueno y un malo. El bueno es el eterno optimista lleno de locas propuestas, el malo es el pesimista, que sospecha de todo y ve desaparecer la carta en la manga. Ramanujan tenía necesidad de que Hardy el crítico frenara su entusiasmo mientras ambos interrogaban a su sospechoso matemático.

De todas formas, no siempre era fácil encontrar un terreno común: con toda seguridad se producía un choque cultural. Mientras Hardy y Littlewood pretendían demostraciones rigurosas, al estilo occidental, los teoremas de Ramanujan simplemente se derramaban, por inspiración de la diosa Namagiri. A veces, Hardy y Littlewood ni siquiera conseguían entender de dónde salían las ideas de su nuevo colega. Hardy observó: «Parecía ridículo angustiarlo preguntándole cómo había descubierto este o aquel teorema ya demostrado, cuando me presentaba media docena diaria de nuevos teoremas».

Ramanujan no sólo tenía que luchar contra el choque cultural-matemático, estaba solo en un mundo extraño hecho de birretes y togas negras; no conseguía encontrar comida vegetariana y escribía a su casa para que le mandaran paquetes de tamarindo y aceite de coco. Si no hubiera sido por el mundo familiar de las matemáticas, probablemente la transición habría sido imposible. Neville, el profesor que había conquistado su confianza en la India, describió aquellos primeros días: «Sufría las pequeñas miserias de la vida en una civilización extraña: el gusto desagradable de las verduras a las que no estaba acostumbrado, los zapatos que le atormentaban los pies que habían sido libres durante veintiséis años. Pero era un hombre feliz, que encontraba alegría en la sociedad matemática en que se estaba introduciendo». Se le podía ver todos los días caminando desgarbado, en zapatillas, por el patio del College, tras renunciar por desesperación a sus zapatos ingleses. Pero, una vez instalado en el despacho de Hardy, con sus libretas abiertas, podía refugiarse en sus fórmulas y ecuaciones mientras Hardy lo observaba, preso en las redes de sus mágicos teoremas. Ramanujan había pasado del aislamiento matemático de la India a la soledad cultural de Cambridge, pero había ganado un compañero con quien explorar su mundo matemático.

Hardy descubrió que dar una educación matemática a Ramanujan era una auténtica obra de equilibrismo: temía que, si insistía demasiado en obligarlo a consumir energías en la demostración de sus resultados, podría «destruir su confianza en sí mismo o romper el sortilegio de su inspiración». Confió a Littlewood el trabajo de familiarizarlo con el rigor de las matemáticas occidental. Littlewood descubrió que se trataba de un trabajo virtualmente imposible: ante cualquier cosa que intentara presentar a Ramanujan, obtenía como respuesta una catarata de ideas originales que lo dejaban clavado en su silla.

Si bien los intentos de Ramanujan por producir fórmulas exactas para contar los números primos contribuyeron a llevar su barco hasta Inglaterra, sería en ámbitos relacionados donde terminaría dejando su marca. La lectura de los comentarios pesimistas de Hardy y Littlewood sobre la malignidad de los números primos lo disuadió de atacarlos directamente. Sólo podemos especular sobre lo que Ramanujan habría podido descubrir si no le hubieran transmitido el miedo de Occidente a los números primos. Junto a Hardy, sin embargo, Ramanujan continuó su exploración de las propiedades relacionadas con ellos. Las ideas que él y Hardy elaboraron contribuirían al primer paso adelante en el camino de una demostración de la conjetura de Goldbach, que afirma que todo número par se puede escribir como suma de dos números primos. Tal progreso llegó por vía indirecta, pero el punto de partida fue la ingenua confianza de Ramanujan en la existencia de fórmulas exactas para expresar sucesiones numéricas importantes, como la de los números primos. En la misma carta en que afirmaba haber encontrado una fórmula para los números primos, decía haber comprendido la manera de generar otra sucesión hasta entonces indomable: la partición de números.

¿De cuántas maneras distintas se puede dividir cinco piedras en montones diferentes? El número de montones varía de un máximo de cinco montones compuestos por una única piedra a un único montón de cinco piedras, con un cierto número de posibilidades intermedias:

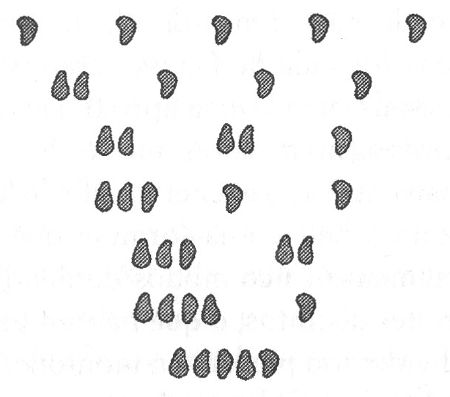
Las siete maneras de repartir cinco piedras.

Estas distintas posibilidades reciben el nombre de particiones del número 5. Como muestra el dibujo, hay siete posibles particiones de 5.

He aquí el número de particiones para los números de 1 a 15:

Ésta es una de las sucesiones numéricas que habíamos planteado en el capítulo 2. Son números que aparecen en el mundo físico casi con la misma frecuencia que los números de Fibonacci; por ejemplo, deducir la densidad de los niveles energéticos en determinados sistemas cuánticos simples se reduce a comprender el crecimiento del número de particiones.

La distribución de estos números no parece tan casual como la de los números primos, pero la generación de Hardy casi había renunciado a encontrar una fórmula exacta que diera su secuencia. Los matemáticos opinaban que, como máximo, podía existir una fórmula que diera una estimación que no se apartara excesivamente del número efectivo de particiones de N, de modo similar al modo en que la fórmula de Gauss para los números primos proporcionaba una buena aproximación la cantidad de números primos no mayores que N. Pero a Ramanujan nunca le habían enseñado a tener miedo de las sucesiones. Estaba decidido a hallar una fórmula que le dijera que existían exactamente cinco modos de dividir cuatro piedras en montones distintos, o que había 3.972.999.029.388 maneras de dividir 200 piedras en montones distintos.

Si bien había fracasado con los números primos, Ramanujan obtuvo un éxito espectacular con las particiones. La capacidad de Hardy para construir demostraciones complejas junto con la ciega confianza de Ramanujan en la existencia de una fórmula exacta se combinaron para conducirlos a su descubrimiento. Littlewood nunca comprendió «por qué Ramanujan estaba tan seguro de que existía una fórmula exacta». Y cuando observamos la fórmula —donde aparecen la raíz cuadrada de 2, π, derivadas, funciones trigonométricas, números imaginarios— no podemos menos que preguntarnos cómo se concibió:

Más adelante Littlewood observó: «Debemos el teorema a una colaboración excepcionalmente feliz entre dos hombres dotados de talentos bien distintos, a la que cada cual dio su mejor contribución, la más característica y afortunada que poseía».

En la cuestión del cálculo de las particiones hay un detalle curioso. La complicada fórmula de Hardy y Ramanujan no proporciona el número exacto de particiones: proporciona una respuesta correcta cuando se la aproxima al número entero más próximo. Así, por ejemplo, cuando insertamos en la fórmula el número 200, obtenemos un valor no entero aproximado a 3.972.999.029.388. Por ello, aunque la fórmula permite obtener la respuesta exacta, produce una cierta frustración el hecho de que no recoja la esencia de estos números. (Más adelante se descubrió una variante de la fórmula que da la respuesta rigurosamente exacta).

A pesar de que Ramanujan no consiguió llevar a buen puerto la misma estratagema en el caso de los números primos, el trabajo que realizó junto con Hardy sobre la función de partición tuvo un impacto importante sobre la conjetura de Goldbach, uno de los grandes problemas irresueltos de la teoría de los números primos. La mayor parte de los matemáticos había renunciado incluso a plantearse este problema: no se había propuesto ni siquiera una sola idea de partida para intentar algún progreso concreto hacia su resolución. Sólo algunos años antes, Landau había declarado que el problema era simplemente inabordable.

El trabajo de Hardy y Littlewood sobre la función de partición inauguró una técnica que hoy se llama método del círculo de Hardy-Littlewood. La referencia al círculo en el nombre del método procede de los pequeños diagramas que acompañaban a los cálculos de Hardy y Ramanujan y que representaban círculos en el mapa de los números imaginarios alrededor de los cuales ambos matemáticos trataban de hacer integraciones. La razón por la que el método se asocia al nombre de Littlewood y no al de Ramanujan está en la utilización que del mismo hicieron Hardy y Littlewood para aportar la primera contribución sustancial a una demostración de la conjetura de Goldbach. Aun no pudiendo probar que todo número par puede expresarse como suma de dos números primos, en 1923 Hardy y Littlewood consiguieron demostrar algo que para los matemáticos era casi igual de importante: que todos los números impares mayores que un número dado (un número enorme) podían escribirse como suma de tres números primos. Pero hacía falta imponer una condición para que su demostración fuera válida: que fuera cierta la hipótesis de Riemann. Por tanto, éste era un nuevo resultado que se subordinaba a que la hipótesis de Riemann se convirtiera tarde o temprano en el teorema de Riemann.

Ramanujan contribuyó a desarrollar aquella técnica, pero desgraciadamente no vivió lo suficiente para ser testigo del inesperado papel que tendría en el desarrollo de las matemáticas. En 1917 estaba cada vez más deprimido. Gran Bretaña se enfrentaba a los horrores de la Primera Guerra Mundial. El Trinity College acababa de nombrar profesor a Ramanujan. La plaza de profesor que ocupaba Russell hacía poco que había sido revocada a causa de su militancia antibelicista y el College no estaba dispuesto a tolerar las posiciones pacifistas de Ramanujan. Aunque finalmente había aprendido a comprimir sus pies dentro de los zapatos occidentales y a llevar toga y birrete, su corazón seguía estando en la India meridional.

Cambridge se había convertido en una prisión: Ramanujan estaba habituado a la libertad que ofrecía la vida en la India, cuyo clima cálido permitía que la gente pasara mucho tiempo al aire libre. En Cambridge tenía que refugiarse tras los gruesos muros del College para protegerse del viento gélido del mar del Norte. Las divisiones sociales le impedían tener relaciones más allá de las interacciones formales de la vida académica. Además, estaba empezando a descubrir que la insistencia de Hardy en el rigor matemático impedía que su mente pudiera vagar libremente por el espacio matemático.

Al declive de su estado psicológico se unía el deterioro físico: el Trinity College no comprendía las rígidas reglas de alimentación que le imponía su religión. En la India estaba acostumbrado a recibir la comida directamente de manos de su esposa mientras él llenaba sus libretas; aunque las cocinas del College le ofrecían un servicio idéntico al que se reservaba para profesores como Hardy y Littlewood, para Ramanujan lo que se servía en el comedor era absolutamente imposible de digerir. Simplemente no era capaz de sobrevivir por sí mismo y se sentía terriblemente solo, ya que había dejado a su esposa y a su familia en la India. Su malnutrición llevó a la sospecha de que había contraído tuberculosis, lo que lo obligó a pasar por una serie de clínicas de reposo.

Ramanujan intentó salir adelante concentrándose en las matemáticas, pero sin mucho éxito. Sus sueños estaban plagados de imágenes matemáticas delirantes. Creía que sus dolores abdominales estaban causados por el clavo sin fin que se elevaba sobre el paisaje de Riemann cuando la función zeta tendía al infinito. ¿Se trataba quizá de un castigo terrible por haber incumplido la ley brahmánica que le prohibía atravesar los mares? ¿Había interpretado mal el mensaje de Namagiri? Desde su llegada a Cambridge su esposa no le había escrito. La presión que tenía que soportar resultaba demasiado fuerte.

Tras un restablecimiento parcial, aún bajo la depresión, Ramanujan intentó suicidarse lanzándose ante un convoy del metro londinense. Falló gracias a la intervención de un guardia que consiguió hacer parar el tren a pocos metros del cuerpo de Ramanujan. En 1917 el intento de suicidio era un delito, pero gracias a la intervención de Hardy se retiraron las acusaciones contra Ramanujan, a condición de que fuera internado en un sanatorio de Marlock, en Derbyshire, donde debería permanecer doce meses bajo control médico.

Ahora Ramanujan estaba en un callejón sin salida: lejos de todo, sin siquiera el estímulo de sus encuentros cotidianos con Hardy. «Llevo un mes aquí —escribió a Hardy—, y no me han permitido encender la calefacción ni un solo día. Me han prometido calefacción para los días de trabajo matemático serio. Esos días no han llegado aún, y yo estoy en esta habitación abierta y terriblemente fría».

Por fin Hardy consiguió trasladar a Ramanujan a un sanatorio de Putney, un barrio de Londres. Por más que él confesara que Ramanujan había sido el único verdadero amor de su vida, su relación estaba casi totalmente falta de sentimiento, si excluimos la emoción de hacer matemáticas juntos. Durante una visita a Ramanujan, que yacía en cama, a falta de tema de conversación Hardy le comentó el número del taxi que lo había llevado hasta allí, 1.729, como ejemplo de un número sin ningún atractivo. Incluso en cama, Ramanujan era irrefrenable: «¡No, Hardy!, ¡no, Hardy!; es un número muy interesante, es el menor número que se puede expresar de dos maneras distintas como suma de dos cubos». Tenía razón: 1.729 = 1³ + 12³ = 10³ + 9³.

La suerte de Ramanujan mejoró ligeramente con su nombramiento como miembro de la Royal Society, la institución científica más prestigiosa de Gran Bretaña, y finalmente también con su nombramiento como profesor del Trinity College. La influencia de Hardy sobre estos nombramientos era la única manera que conocía de expresar el amor del que hablaba. Pero Ramanujan nunca recobró la salud: al terminar la Primera Guerra Mundial, Hardy sugirió que quizá debería volver a la India para completar su convalecencia. El 26 de abril de 1920, Ramanujan murió en Madrás a la edad de treinta y tres años, a causa de una enfermedad que hoy se cree que podía ser amebiasis, una infección del intestino grueso que probablemente había contraído antes de marchar a Inglaterra.

A pesar de que Ramanujan finalmente no consiguió dominar los números primos, su primera carta a Hardy tuvo un efecto duradero sobre la teoría de estos números. Los matemáticos están convencidos de que la respuesta a este enigma irresuelto puede aparecer en cualquier momento y a partir de cualquier fuente. Una nueva intuición podría proyectar un nombre antes desconocido desde las sombras de una existencia oscura a las luces de los focos. Como demostró el caso de Ramanujan, quizás el conocimiento y las expectativas pueden llegar a frenar los progresos: los académicos que se han formado en las sedes tradicionales de la cultura no necesariamente están en la mejor posición para escapar de los esquemas. Siempre existe la posibilidad de que otro sobre voluminoso acabe en el escritorio de algún matemático, anunciando la llegada de un genio desconocido preparado para convertir en realidad el sueño de Ramanujan de descifrar el enigma de los números primos.

Las ideas que Ramanujan dejó tras de sí estaban destinadas a alimentar el trabajo de generaciones enteras de matemáticos, y continúan haciéndolo. De hecho, podría afirmarse que sólo en los últimos decenios se ha empezado a apreciar completamente el valor real de las ideas de Ramanujan. Incluso a la muerte de Hardy, el verdadero alcance de las fórmulas de Ramanujan no era todavía evidente; el propio Hardy fue muy crítico con una de las conjeturas de Ramanujan: «Parece que hayamos ido a parar a uno de los páramos de las matemáticas», observó en uno de sus escritos en relación con ella. Sin embargo, con la distancia de los años podemos emitir un juicio bien distinto sobre la importancia de la conjetura tau de Ramanujan, que es como se la conoce, ya que en 1978 su solución le valió a Pierre Deligne la concesión de una medalla Fields. Bruce Berndt, uno de los grandes admiradores de Ramanujan, lo ha comparado con Bach, que tras su muerte cayó en el olvido durante años.

Berndt dedicó buena parte de su propia vida a analizar los cuadernos inéditos de Ramanujan: se trata del continuador de una tradición de matemáticos que quedaron fascinados por la masa de fórmulas y de ecuaciones que generó Ramanujan. Explorando los cuadernos, Berndt descubrió una curiosa tabla que entra en los detalles de la cantidad de números primos para N menor que 100.000.000; los valores son correctos totalmente, o casi, además, son más precisos de los que da la fórmula que Ramanujan envió a Hardy en su primera carta. Sin embargo, no hay ningún indicio sobre cómo los dedujo.

¿Podría ser que Ramanujan hubiera accedido a una fórmula secreta para calcular la distribución de los números primos, una fórmula tan precisa como la relativa a la función de partición? ¿Podría ser que los cuadernos de Ramanujan escondan aún indicios a la espera de ser descubiertos? En 1976 la comunidad matemática se estremeció ante la noticia del descubrimiento de un cuaderno de Ramanujan que se creía perdido, y que resultó estar repleto de matemáticas inéditas; este descubrimiento está destinado inevitablemente a alimentar hipótesis sobre la posibilidad de que, escondidos en los archivos del Trinity College o en cualquier cajón de Madrás, haya tesoros que todavía no han visto la luz y que explicarían la capacidad de Ramanujan de contar los números primos con tanta precisión.

La muerte de Ramanujan supuso una gran conmoción para Hardy, quien sólo dos meses antes había recibido de su amigo una carta «más bien alegre y llena de matemáticas». La pérdida de tan maravilloso compañero de viaje en sus excursiones a través del territorio matemático le produjo una gran desolación: «Para mí, su originalidad ha sido fuente constante de inspiración desde que lo conocí, y su muerte es uno de los peores golpes que jamás haya recibido».

Cuando envejeció, Hardy cayó víctima de la depresión. Siempre había pensado en sí mismo como si fuera joven; ahora, la imagen de su cara cruzada de arrugas le repugnaba tanto que cogió la costumbre de pedir insistentemente que dieran la vuelta a todos los espejos cuando entraba en una habitación. Odiaba los efectos de la edad sobre su capacidad de hacer matemáticas. Su Apología de un matemático es la descripción memorable de un matemático al final de su carrera: para hacer matemáticas, un matemático «no ha de ser demasiado viejo, las matemáticas son un ejercicio creativo y no contemplativo, y nadie puede consolarse cuando pierde el poder o el deseo de crear; y tal cosa es fácil que le ocurra muy pronto a un matemático».

Como antes había hecho Ramanujan, Hardy intentó quitarse la vida, aunque escogió tomar pastillas en lugar de saltar ante un tren. Sin embargo vomitó las pastillas y quedó tuerto. C. P. Snow recuerda una visita que hizo a Hardy tras su intento de suicidio: «Se burlaba de sí mismo. Se las arreglaba muy mal. ¿Había existido alguien que se las arreglara peor que él?». El único consuelo para Hardy, como escribió en la Apología, había sido Ramanujan: «Todavía hoy, en los momentos de depresión, cuando estoy obligado a escuchar a gente pedante y presuntuosa, me digo: “bueno, he hecho una cosa que vosotros nunca seréis capaces de hacer: he colaborado con Littlewood y Ramanujan casi de igual a igual”».