5. LA ESFINGE Y SUS ENIGMAS

Pese a que los descubrimientos de Hubble fueron revolucionarios, al cabo de un tiempo resultó evidente que no todo era un lecho de rosas para la teoría del big bang. Si bien ningún hecho conocido cuestionaba el modelo —hasta el día de hoy es una especie de bastión inexpugnable que resiste la confrontación de todos los hechos observados—, algunas características del universo seguían sin explicación, de modo que se planteaban preguntas inquietantes como éstas: ¿por qué el universo tiene el mismo aspecto aun a distancias tan enormes? Además, ¿por qué existe el universo?

Se puede hacer una lista de media docena de enigmas similares que se conocen en conjunto como problemas cosmológicos o, más sencillamente, como misterios del big bang, y que han sido tema de muchas polémicas y trabajos fundamentales en los últimos tiempos. Intentar resolverlos no implica dejar de lado la teoría del big bang tal como hoy la concebimos, pues sabemos que no puede cuestionarse ya el modelo en general. En cambio, en una suerte de giro freudiano, los cosmólogos buscan ahora los indicios del comportamiento adulto del universo en la primera infancia del big bang. Abrigan la esperanza de sustituir la explosión misma o, tal vez, lo que sucedió en la mínima fracción de segundo inmediatamente posterior, por algo menos excesivo, algo que signifique un nacimiento y una infancia del universo menos traumáticos. Desde ya, esta operación no plantea conflicto alguno con las observaciones, puesto que no tenemos acceso directo a las etapas primigenias del universo. Tal vez la respuesta a todos los enigmas radique en plantear una especie de explosión modificada.

En la Gran Bretaña de la década de 1990, cuando me recibí de físico, todos los enigmas del big bang planteados estaban en auge y representaban un verdadero desafío para cualquier aprendiz de cosmólogo. Sobre todo, indicaban que ese campo de investigación estaba presto para las innovaciones, pues había interrogantes fundamentales a la espera de nuestras especulaciones y nuestra imaginación. Recuerdo claramente que me di cuenta con sorpresa de que aún había espacio para el trabajo creativo en cosmología después de toda la batahola que había generado la teoría del big bang. Mientras asistía a los cursos de posgrado en Cambridge, empecé a pensar que esos enigmas eran razón suficiente para elegir la cosmología como carrera en lugar de otras fascinantes ramas de la física de avanzada, como la teoría de las cuerdas o la física de partículas. La teoría de las cuerdas carecía de datos, era mera especulación; la física de partículas estaba plagada de datos pero, a mi juicio, quedaba en ella muy poco lugar para una labor realmente creativa. La cosmología, en cambio, era ideal: se basaba en la realidad pero era aún muy tierna, de modo que en ella quedaban problemas fundamentales sin resolver.

El enigma más sencillo vinculado con el big bang ha recibido el nombre de «problema del horizonte» porque los observadores del cosmos sólo pueden ver una pequeña porción del universo. Están rodeados por un horizonte, más allá del cual no pueden ver. En nuestra experiencia cotidiana todos sabemos que no podemos ver la totalidad de la Tierra sino sólo lo que está dentro de nuestro horizonte. Los habitantes de un universo originado por el big bang padecen un problema de perspectiva similar, con la salvedad de que el efecto horizonte sobre la Tierra se debe a su curvatura mientras que el efecto horizonte en el universo es producto de dos fenómenos de índole muy distinta. El primero es el hecho de que haya un límite universal para las velocidades, la velocidad de la luz. El segundo es el hecho incontrovertible de que un universo producido por el big bang tiene una fecha de nacimiento y, por consiguiente, una edad finita en cada momento. De la combinación de esas dos circunstancias se infiere de inmediato la existencia de horizontes: la creación implica limitación.

Cuando miramos una estrella distante en el cielo, la vemos como fue en el pasado. Vemos la luz que emitió la estrella hace mucho, y que luego tardó todo el tiempo transcurrido desde entonces en llegar a nosotros. Algunas estrellas visibles distan de nosotros alrededor de mil años luz, lo cual significa que las vemos tal como eran hace mil años. En el lapso de mil años transcurridos desde entonces, la imagen que vemos atravesó el espacio hasta llegar a ser visible.

Seamos ahora megalómanos y pensemos en lugares cada vez más remotos, imaginemos las enormes distancias que han sondeado los astrónomos posteriores a Hubble. Cuanto más lejos miramos, tanto mayor es la demora entre el momento en que la imagen se originó y el momento en que la vemos. Por consiguiente, cuando sondeamos el espacio, sondeamos de hecho el pasado. Si observamos galaxias que distan de nosotros mil millones de años luz, las vemos como fueron hace mil millones de años. Vemos sombras nada más, sombras del pasado y de objetos que tal vez ya no existen: nunca lo sabremos.

Por ende, los cosmólogos disfrutan de ciertas ventajas con respecto a los arqueólogos, puesto que tienen acceso directo al pasado del universo; para verlo sólo tienen que mirar suficientemente lejos. Sin embargo, de esta situación se infiere una conclusión inquietante. Mirando cada vez más lejos, alcanzamos distancias que corresponden a un pasado remotísimo, comparable con la edad del universo, 15 mil millones de años. Es evidente que no podemos ver nada más allá: esas distancias determinan nuestro horizonte cosmológico. Esto no quiere decir que no exista nada más allá, seguramente ocurre todo lo contrario. No obstante, no podemos ver esas regiones porque la luz que emiten desde el big bang no ha tenido tiempo aún de llegar a nosotros.

Si la luz se desplazara a velocidad infinita, el efecto horizonte no existiría. Análogamente, si hubiera algo más veloz que la luz, podríamos saber algo de las regiones que están más allá de nuestro horizonte, en el caso de que emitieran señales a través de ese canal ultrarrápido. Por último, si la velocidad de la luz no fuera constante y fuera posible acelerarla moviendo su fuente, por ejemplo, también podríamos ver objetos situados más allá del horizonte con la condición de que se movieran hacia nosotros con velocidad suficiente. Lamentablemente, la velocidad de la luz es una constante finita que actúa como límite universal de las velocidades y crea por consiguiente el efecto horizonte para cualquier universo de edad finita.

En sí misma, la existencia de horizonte no constituye un problema. El problema, en realidad, es el tamaño del horizonte inmediatamente después del big bang. Cuando el universo tiene un año de edad, el radio del horizonte es de sólo un año luz. Cuando el universo tiene un segundo de edad, el radio del horizonte es la distancia que puede recorrer la luz en un segundo, 300.000 km, la distancia entre la Tierra y la Luna. Cuanto más nos acercamos al big bang, tanto más pequeño es el horizonte.

Por consiguiente, el universo recién nacido está fragmentado en diminutas regiones que son mutuamente invisibles. Lo que nos causa problemas es esta especie de miopía vinculada con los primeros instantes del universo, pues nos impide encontrar una explicación física —es decir, una explicación fundamentada en interacciones físicas— de por qué el universo parece tan homogéneo aunque es tan inmenso. ¿Cómo explicar la homogeneidad del universo mediante un modelo físico? Por lo general, los objetos se homogeneízan cuando sus distintas partes entran en contacto y adquieren así características comunes. Por ejemplo, el café con leche se homogeneíza revolviéndolo, permitiendo que la leche se diluya en el café.

Sin embargo, el efecto horizonte excluye un proceso semejante, pues indica que en el comienzo las vastas regiones del universo que hoy vemos tan homogéneas no pudieron tener noticia unas de otras. Menos aún pudieron entrar en contacto. Así pues, el modelo del big bang impide explicar la homogeneidad del universo, hecho algo escalofriante porque parece que hubiera existido una suerte de comunicación telepática entre regiones totalmente aisladas entre sí.

De alguna manera, algo debe haber ensanchado los horizontes del universo en su infancia y generado su homogeneidad, dando origen al modelo del big bang. De inmediato resulta evidente que uno de los enigmas del big bang, el de la homogeneidad del universo en vista del efecto horizonte, reclama a gritos que reemplacemos la teoría del big bang por algo más fundamental. Se abren las puertas a la especulación.

Esa era la cuestión que me atormentaba en el invierno de 1995, mientras caminaba por el campo de St. John’s College. Se trata de algo que parece fácil de resolver hasta que uno lo intenta, pero después de intentarlo, se transforma en una pesadilla, como descubrí en aquel entonces. No obstante, había otro misterio que amenazaba ya con martirizarme aún más: el problema de la planitud. Se trata de algo vinculado con la caprichosa dinámica de la expansión y su relación con la «forma» del universo, pero me temo que lleve algún tiempo explicarlo.

Volvamos imaginariamente a la época en que Einstein pensaba que el universo debía ser estático, antes de los descubrimientos de Hubble. Mientras Einstein se aferraba a sus prejuicios, el físico ruso Alexander Friedmann partió de la teoría de la relatividad y desarrolló todas las deducciones matemáticas que indicaban que el universo debía estar en expansión. Contra todo lo que podía esperarse, considerando sus respectivas carreras, Friedmann dedujo la expansión del universo.

En los congresos internacionales, la celeridad de los científicos rusos para reivindicar su prioridad con respecto a cualquier descubrimiento realizado en Occidente se ha transformado ya en motivo de broma. Basta que alguien presente un trabajo sobre válvulas de inodoro para que se levante algún Dimitri y comience a decir a gritos desde la última fila del auditorio que el inodoro y todas sus piezas accesorias fueron inventadas en Rusia decenios antes de que en Occidente se conociera la existencia de la mierda. No obstante, algunas veces los rusos tienen razón en sus reclamos; tal es el caso de la cosmología moderna. En Occidente parece haber una voluntad de olvidar que, después del gran error cometido por Einstein a fines de la década de 1910 y antes de que Hubble descubriera la expansión cósmica diez años más tarde, Alexander Friedmann llegó a la conclusión de que el cosmos se expandía partiendo de la teoría general de la relatividad. Como bien dicen sus compatriotas, Friedmann debería ocupar un lugar similar al de Copérnico, aquel monje que colocó al Sol en el centro de nuestro sistema, porque a él se debe un cambio de perspectiva de análoga importancia en la cosmología, cambio que abriría las puertas a la idea de un universo no estático.

Tal vez Friedmann sería más conocido si su vida hubiese sido menos rica en acontecimientos y su indiscutible talento hubiera seguido caminos más trillados. Pero su vida fue arrastrada por los acontecimientos históricos, pues abarcó el período de agitación política de 1905, la Primera Guerra Mundial, la revolución comunista y la posterior guerra civil. En 1915 (mientras en otro lugar, un Einstein mucho mejor alimentado redondeaba la teoría general de la relatividad), Friedmann escribió a un amigo:

Mi vida es bastante rutinaria, a excepción de algunos accidentes como una explosión de metralla a seis metros de distancia, el estallido de una bomba austríaca a menos de treinta centímetros que no tuvo consecuencias demasiado graves y una caída que sólo me acarreó un corte en el labio superior e intensos dolores de cabeza. Pero uno se acostumbra a todo, desde luego, especialmente cuando echa una mirada alrededor y ve que suceden cosas mucho más atroces.

La destreza matemática de Friedmann no tenía parangón y brillaba aun en tiempos tan agitados, especialmente en el cálculo de las trayectorias de las bombas que se lanzaban desde los aeroplanos. A menudo hacía dos papeles a la vez, el de ingeniero aeronáutico y el de piloto de pruebas.

Esas experiencias lo amargaron bastante y uno tiene la impresión de que su retraimiento se debía en parte a su bochorno ante el modo como la historia había mezclado el horror y la ciencia en el curso de su vida. En los pocos momentos de sosiego, hizo también investigaciones de vanguardia que tenían aplicaciones pacíficas en campos tan dispares como la meteorología, la dinámica de fluidos, la mecánica y la aeronáutica, entre otros. Por otra parte fue uno de los primeros en realizar viajes en globos aerostáticos, en los cuales rompió récords de altura mientras llevaba a cabo experimentos de meteorología y medicina a bordo.

Tenía una energía excepcional, electrizante. En los momentos de mayor calma, desarrollaba una intensa actividad docente, hacía tareas administrativas y llevaba adelante investigaciones. En su calidad de funcionario, desempeñó un papel decisivo en la creación de muchos institutos de investigación en la Unión Soviética y se ocupó permanentemente de reunir fondos para salarios, equipos de laboratorio y bibliotecas. En calidad de docente, solía tener tres trabajos de tiempo completo simultáneamente.

En 1922, a los 34 años, Friedmann se interesó por la teoría de la relatividad y estudió aplicadamente la teoría general. A raíz de la guerra y el posterior bloqueo impuesto a la Unión Soviética, la teoría general de la relatividad se conoció en Rusia con varios años de atraso. Friedmann fue uno de los primeros en estudiarla y en escribir artículos sobre ella en ruso. En su afán por garantizar que la nueva generación de su patria no se perdiera los últimos avances de la ciencia, preparó varios libros de texto y artículos de divulgación sobre el tema. Al mismo tiempo, inició cálculos propios entreteniéndose con el nuevo juguete que Einstein le había obsequiado a los físicos.

Muy poco es lo que se sabe del carácter de Friedmann, ya que era una de esas personas que se destacan más por sus acciones. Así, aunque no podamos decir que comprendemos sus razonamientos, es indiscutible que no compartía los prejuicios cosmológicos de Einstein. Cuando aplicó las ecuaciones de la relatividad general al universo en su totalidad y dedujo que estaba en expansión, no lo arrebató el pánico. Tomó las cosas como eran —nada de constantes cosmológicas— y en 1922 publicó sus conclusiones en una revista alemana. Por consiguiente, predijo la expansión del universo antes de que Hubble hiciera sus observaciones.

El artículo de Friedmann disgustó mucho a Einstein y lo empujó a dar una vuelta más a la historia, de modo que la espina de la constante cosmológica terminó clavándose aún más profundamente en su carne. En esa época, Einstein abrigaba la esperanza de que su ecuación de campo tuviera una única solución cosmológica: un universo estático que podría deducirse entonces por métodos puramente teóricos evitando difíciles observaciones astronómicas. Para él, podía haber otras soluciones que en última instancia resultarían incompatibles con la ecuación de campo por una razón u otra. A partir de esta creencia, cuando leyó el artículo de Friedmann pensó que los resultados del ruso no tenían nada que ver con el mundo real, pero también creyó que encerraban errores matemáticos.

En una actitud no muy frecuente en él, pocas semanas después de publicado el artículo de Friedmann, envió una nota muy desagradable a la misma revista atacando el trabajo. Decía allí: «Los resultados relativos a un universo no estacionario que contiene el artículo [de Friedmann] me parecen sospechosos. De hecho, se puede comprobar que la solución ofrecida no satisface las ecuaciones de campo».

No hay duda de que Friedmann, como todos, veneraba a Einstein y probablemente se sintió muy afligido cuando leyó la nota. Repitió meticulosamente todos sus cálculos una y otra vez, con la sensación quizá de que estaba sentenciado. Por último, tuvo que admitir lo increíble: el gran Einstein se había equivocado y sus cálculos originales eran correctos. Redactó una respetuosa carta al maestro explicando sus deducciones y señalando el lugar en que, según creía, Einstein se había equivocado. Era un error tan elemental que Einstein lo advirtió de inmediato al leer la carta y se retractó de la nota anterior, presumiblemente con cierto embarazo. Debe haberse sentido muy decepcionado, no tanto porque había cometido un error, sino porque sus ecuaciones no aportaban una solución única que permitiera concebir el universo según sus creencias más queridas.

En la segunda nota, Einstein gentilmente reconoció su error:

En mi nota anterior critiqué [el artículo de Friedmann]. No obstante, mi objeción […] partía de un error en los cálculos. Considero que los resultados del señor Friedmann son correctos y esclarecedores: muestran que, además de la solución estática, existen soluciones que varían con el tiempo.

Así y todo, en el borrador de puño y letra escrito por Einstein que ha llegado hasta nuestros días, se puede leer una frase que tachó: «Difícilmente se pueda atribuir algún significado físico a esas soluciones».

Es evidente que se habría sentido muy feliz de agregar ese comentario, pero, puesto que no había pruebas para respaldarlo, su honestidad se impuso.

Me veo obligado a describir con algún detalle los notables artículos de Friedmann, pues definen el modelo fundamental de universo sobre el cual se basan las teorías de cualquier cosmólogo. Además, dan origen a uno de los problemas más difíciles de la cosmología, el de la planitud. Friedmann presenta tres tipos de modelo: los espacios esféricos o cerrados, los seudoesféricos o abiertos y los universos de geometría «plana». Son términos que describen la forma misma del espacio, trama fundamental del universo. A continuación, el físico ruso muestra que, según la teoría general de la relatividad, esos modelos deben ser expansivos —al menos si no se usan artilugios como la constante cosmológica Lambda—, de modo que predice de hecho los descubrimientos de Hubble.

Si esos artículos no existieran, los descubrimientos de Hubble casi no tendrían sentido. Se dice a veces que nunca debemos adoptar una teoría científica hasta que los experimentos no la comprueben. Sin embargo, un célebre astrónomo también dijo que nunca debemos creer en una observación si no está respaldada por una teoría. Pues bien, unos diez años antes de los descubrimientos de Hubble, los artículos de Friedmann aportaron la teoría necesaria para interpretarlos.

Friedmann empieza por aclarar la noción de expansión cósmica y formula la interpretación que le damos hoy, eliminando algunas paradojas que podrían filtrarse en la teoría en caso contrario. Muestra que la expansión no es un movimiento mecánico como muchos creen sino que es un efecto geométrico. Debo reconocer que hasta aquí, yo mismo he utilizado esa interpretación errónea; permítame el lector ahora corregir lo dicho y explicar con mayor precisión qué significa realmente la expansión según la teoría de la relatividad.

En la imagen relativista de la expansión, los componentes del fluido cosmológico, es decir, las galaxias, están incrustadas en el espacio y, por consiguiente, no tienen movimiento relativo con respecto a él. En cambio, el propio espacio está en movimiento, se expande y, a medida que transcurre el tiempo, genera cada vez más espacio entre dos puntos dados cualesquiera. Así, la distancia entre dos galaxias cualesquiera se incrementa con el tiempo y crea la ilusión de un movimiento mecánico. Sin embargo, en la realidad, las galaxias están ahí, viendo, por así decirlo, que el universo genera cada vez más espacio entre ellas. Aunque al lector esta diferencia le parezca demasiado sutil, le pido que intente digerirla. Es la fuente de más de un malentendido en cosmología.

Hay una analogía posible: pensemos en una Tierra hipotética cuyos habitantes se vieran confinados a la superficie sin poder verla desde el espacio. Imaginemos ahora que esa superficie se expande, como si la Tierra se inflara como un globo, aunque el espacio exterior siga siendo inaccesible para sus habitantes. Si observáramos las ciudades de esa Tierra en expansión, comprobaríamos que en realidad no se mueven aunque la distancia que las separa aumenta. En esa situación imaginaria, las ciudades no tienen patas para desplazarse, pero, de algún modo, la dinámica misma del espacio en que residen crea la ilusión de movimiento porque la distancia entre ellas crece.

Esta sutileza es fundamental para la coherencia de la teoría. Si la expansión cósmica fuera un movimiento en el sentido habitual del término, caeríamos fácilmente en paradojas. Por ejemplo, la ley de Hubble indica que la velocidad de recesión de las galaxias es proporcional a su distancia. Si esa velocidad fuera genuina, es decir, si describiera un movimiento en un espacio newtoniano fijo, podríamos hallar una distancia más allá de la cual la velocidad de recesión sería mayor que la velocidad de la luz.

De hecho, la velocidad de todas las galaxias es nula con respecto al espacio que las contiene, como ocurría con las ciudades imaginarias de nuestro hipotético ejemplo de la Tierra en expansión. No obstante, la distancia entre las galaxias aumenta con el transcurso del tiempo a un ritmo posiblemente mayor que el de la velocidad de la luz, si se toman en cuenta galaxias suficientemente lejanas. No hay contradicción entre estas dos proposiciones y, por lo tanto, no hay paradoja ni contradicción alguna con la teoría especial de la relatividad.

No obstante, la ley de Hubble tiene una interpretación en la concepción de Friedmann. Según el físico ruso, vivimos en un universo en expansión cuyo modelo sería un espacio en el cual las distancias se multiplican por un número que se denomina factor de expansión o factor de escala. Este factor aumenta con el transcurso del tiempo, lo que implica una expansión geométrica. Sin embargo, como todas las distancias se multiplican por ese factor, cuanto mayor es la distancia, tanto más grande es el incremento. No ocurriría lo mismo si se sumara un número a todas las distancias, pero ocurre que el factor de expansión es multiplicativo: a mayor distancia, mayor es el incremento a lo largo del tiempo.

En consecuencia, si volvemos a la concepción de Hubble y describimos la expansión como un movimiento real en un espacio newtoniano, parece que la «velocidad» es proporcional a la distancia, que es precisamente lo que dice la ley de Hubble. Pero la concepción de Friedmann es más compleja aún, pues muestra que el movimiento hacia afuera que Hubble observó más tarde no tiene realmente un centro: cualquier observador tiene la ilusión de que es el centro de un movimiento hacia afuera —hecho que satisface la ley de Hubble— porque en realidad la totalidad del espacio se estira con igual ritmo en todas partes.

Una vez aclarado este punto, Friedmann postuló, como Einstein, que el fluido cosmológico es homogéneo, es decir, tiene el mismo aspecto o las mismas propiedades en todo el universo. Más que provenir de los datos, los motivos para formular ese postulado son intuitivos y de conveniencia matemática (por no hablar de haraganería). Debemos recordar que todos esos razonamientos se hicieron años antes del descubrimiento de Hubble. De hecho, por respeto al rigor histórico, tanto Einstein como Friedmann pensaron en un fluido homogéneo de estrellas, y no de galaxias, de las cuales no tenían noticia. Por un verdadero milagro, los dos hicieron una suposición correcta, aunque con algunos ingredientes erróneos.

Suponer la homogeneidad limita abruptamente el número de geometrías o espacio-tiempos que se pueden utilizar para describir el universo. Si la materia genera curvatura y si la densidad del fluido cosmológico es la misma en todas partes, la curvatura del universo también debe ser la misma en todas partes. Quedan descartadas así las formas curvas irregulares o estrafalarias: por ejemplo, el universo no puede tener la forma de un elefante, bestia que está muy lejos de ser homogénea. Nos quedan, en realidad, sólo tres posibilidades.

La más sencilla es un espacio tridimensional que no tiene curvatura: el espacio euclidiano. Para ayudar a imaginar los otros dos casos, en la figura 1.a he dibujado un símil bidimensional de un espacio tridimensional real, una hoja plana infinita. Al lector quizá lo sorprenda saber que semejante superficie plana es una de las posibilidades, dado que la materia genera curvatura; pero debe recordar que la materia curva el espacio-tiempo, y no hemos considerado todavía cómo opera el tiempo en este universo.

Veamos cómo abordó Friedmann la cuestión del tiempo. Primero postuló que todas las distancias medidas sobre la hoja plana debían multiplicarse por el factor de escala o de expansión del universo. Es posible que el factor varíe con el transcurso del tiempo, lo que daría origen a una dinámica temporal en semejante universo. El modelo de espacio-tiempo correspondiente, entonces, es ese ente combinado: la superficie más un factor de escala que depende del tiempo, entidad que se curva por acción de la materia según las ecuaciones de campo de Einstein. En efecto, cuando Friedmann introdujo esta geometría en las ecuaciones de campo, halló que la entidad es curva. En la figura 2 he graficado el factor de escala en función del tiempo para ese universo.

Se puede observar en la figura que el factor de escala de un universo de geometría plana aumenta con el tiempo, aunque la tasa de incremento disminuye. Esa disminución puede interpretarse como la curvatura del espacio-tiempo. Como veremos más adelante, el destino de semejante universo es excepcional. Si miramos más atentamente la figura 2, veremos que se expande eternamente y que su velocidad de expansión disminuye gradualmente pero jamás se detiene del todo.

Los otros dos espacios son más complejos. Uno de ellos corresponde a la esfera [superficie esférica]^[16], que tiene curvatura idéntica en todos sus puntos. Parece algo fácil de imaginar, pero recordemos que estamos hablando de una superficie esférica tridimensional [de una esfera de cuatro dimensiones], no de su equivalente bidimensional. He creado una versión para jardín de infantes en la figura 1.b; si el lector puede «ver» cómo es, lo felicito; yo no puedo, pero no por ello he dejado de trabajar con superficies esféricas tridimensionales. Esa es la ventaja de las matemáticas; nos permiten jugar con objetos que nuestro cerebro no puede imaginar.

Si las esferas tridimensionales son desconcertantes, el tercer tipo de espacio homogéneo lo es aún en mayor grado. Se lo llama seudoesfera o universo abierto. En la figura 1.c he trazado un fragmento de su símil bidimensional; se trata de una superficie infinita en forma de silla de montar. Para contribuir a la comprensión de la seudoesfera, en la figura 3 he usado un artilugio: las secciones trazadas son ortogonales entre sí. En una superficie esférica, en los dos casos se obtiene una circunferencia, razón por la cual se dice a veces incorrectamente que la superficie esférica es el producto de dos circunferencias. Lo mismo ocurre con la seudoesfera, sólo que en ese caso la curvatura de las dos secciones es opuesta. Por eso decimos que esa superficie tiene curvatura negativa, mientras que la superficie esférica habitual tiene curvatura positiva. Así, según la curvatura de las dos secciones, el espacio será finito (como en una superficie esférica) o infinito (como en la seudoesfera).

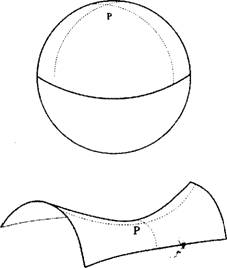
Figura 5 (a) Si trazamos dos secciones ortogonales por cualquier punto (P) de una superficie esférica se generan dos circunferencias que se curvan en la misma dirección (en este caso, hacia abajo). (b) La misma operación aplicada a la superficie de una hiperesfera genera dos líneas que se curvan en direcciones opuestas (una de ellas se curva hacia arriba y la otra hacia abajo.

A fin de indicar cómo se combinan estas dos superficies con el tiempo para generar un espacio-tiempo, debemos multiplicar todas sus distancias por un factor de escala o de expansión, que puede depender del tiempo. Cuando Friedmann aplicó esas geometrías a la ecuación de campo de Einstein y estudió la evolución del factor de expansión, descubrió que esos espacios tienen un destino aciago, a diferencia del modelo de geometría plana descripto anteriormente. Comprobó que el universo esférico se expande a partir de un big bang pero finalmente se detiene y comienza a contraerse para acabar en un big crunch. En cambio, el universo correspondiente a la seudoesfera se expande también a partir de un big bang pero jamás cesa de expandirse: a diferencia de lo que sucede en el modelo de geometría plana, la desaceleración de la expansión no continúa en él indefinidamente sino que alcanza un ritmo estable. En la figura 2 se grafica la evolución del factor de escala en función del tiempo según Friedmann para los tres modelos posibles.

Nos hemos encontrado antes con la misma antítesis, que no refleja más que una tensión que ya hemos debatido: la guerra entre la expansión y la atracción gravitatoria, o el hecho de que, por un lado, el espacio «se infla» y, por el otro, la fuerza de la gravedad actúa en sentido contrario, empujando todo hacia adentro y tendiendo a congregarlo. La evolución del modelo cerrado o esférico es tal que la gravedad finalmente supera la expansión, de modo que esta última prosigue aunque permanentemente desacelerada por la gravedad, hasta que por fin se detiene y precipita al universo en una contracción cada vez más rápida que termina en el colapso final. En los modelos abiertos o seudoesféricos, por el contrario, la expansión gana la batalla, y el universo acaba por escapar a su propia gravedad. Durante algún tiempo, la gravedad tiene intensidad suficiente para desacelerar la expansión, pero al final, la expansión es tan veloz —o, según otro punto de vista, la materia del universo ha quedado tan diluida— que la gravedad ya no tiene importancia. Por esa razón, la expansión ya no se frena y comienza una fase en la cual el universo «escapa de sí mismo» y se transforma en algo vacío.

Una delgada línea separa a esos dos polos: el modelo de geometría plana —un modelo de mesura británica podríamos decir—, en el cual se produce un equilibrio perfecto entre la expansión y la gravedad. La expansión nunca se libra del todo de la gravedad, pero la gravedad jamás consigue detener la expansión y causar un colapso. El universo se expande por toda la eternidad con verdadera flema y moderación, sin ceder ante la gravedad que lo precipitaría en una implosión catastrófica y sin abandonarse a la expansión descontrolada y el posterior vacío, evitando así con gran sensatez el cataclismo o la muerte, para seguir viviendo hasta alcanzar una edad avanzada y venerable.

La longevidad de los modelos de geometría plana es crucial, pues sólo esos universos viven el tiempo necesario para que la materia se aglutine formando estrellas y galaxias, y para que las escalas de tiempo sean tan grandes que permitan la formación de estructuras y de vida. Puesto que no podemos acelerar el lento proceso por el cual la selección natural genera la inteligencia, sólo hay un tipo de modelo que garantiza el tiempo necesario para que ella actúe sin peligro de una hecatombe cósmica.

Ahora bien, los modelos planos son intrínsecamente inestables porque dependen de un precario equilibrio entre el movimiento cósmico y la gravedad; por milagro, evitan dos finales igualmente catastróficos. La menor desviación de la planitud implica que el espacio-tiempo se cierra sobre sí mismo o se transforma en una superficie tipo silla de montar y se vacía. En cualquiera de los dos casos, se precipita vertiginosamente hacia la muerte. De hecho, parecería entonces que el universo ha estado caminando sobre una cuerda floja durante 15 mil millones de años, algo sumamente improbable, si no francamente imposible. Esto se conoce como problema de la planitud, segundo enigma del big bang que ha acosado a los cosmólogos desde que Friedmann develó el panorama de la cosmología relativista.

Existe una descripción posible de esta pulseada, un número que se llama Omega (como la letra griega). Omega es aproximadamente igual al cociente entre la energía gravitatoria del universo y la energía implícita en su movimiento de expansión. En el universo de geometría plana, ambas cantidades son iguales en todo momento, de modo que Omega es igual a uno. En los modelos cerrados, Omega es mayor que uno pues su energía gravitatoria es mayor que su energía cinética; en los modelos abiertos, Omega es menor que uno.

Omega se puede expresar de una manera equivalente, definiendo, para una velocidad de expansión determinada, la densidad de materia que genera la cantidad exacta de energía gravitatoria necesaria para equilibrar la energía de expansión. Esta densidad se denomina crítica, siguiendo la nomenclatura de las armas nucleares. Es la densidad necesaria para que Omega sea igual a 1 permanentemente, es decir, necesaria para la planitud. Si la densidad cósmica supera este valor crítico, la gravedad gana la partida y nos hallamos frente a un modelo cerrado. Por el contrario, si la densidad es menor que el valor crítico, tenemos la certeza de que en ausencia de gravedad el universo acabará por «escapar de sí mismo» mediante una explosión, y nos hallamos frente a un modelo abierto. No sorprende pues que Omega se pueda expresar como el cociente entre la densidad cósmica real y la densidad crítica, y que ese valor describa el estado actual de ese gigantesco tira y afloja.

El problema de la planitud es tan poco dócil a cualquier tratamiento porque, a medida que el universo se expande, las desviaciones del valor 1 de Omega aumentan abruptamente, como se puede ver en la figura 4. En el modelo de geometría plana, Omega es igual a uno eternamente, pero el menor exceso de un tipo de energía sobre el otro, es decir, la menor diferencia entre la densidad cósmica real y la crítica genera una situación que sólo puede empeorar y que, de hecho, empeora rápidamente.

El padre del universo inflacionario, Alan Guth, cuenta que ese problema lo obsesionaba en los meses anteriores a su gran descubrimiento. Tenía entonces poco más de treinta años y estaba en un momento decisivo de su carrera, de modo que no tenía por qué preocuparse por la cosmología, que en ese entonces no era una rama respetable de la física. Se la veía como una empresa que cualquier joven científico debía evitar como si fuera la peste, dejándola en manos de hombres más maduros, víctimas de atrofia cerebral.^[17]

Guth sufría presiones para publicar rápidamente aburridos trabajos encuadrados dentro de las principales tendencias imperantes en la física, pero hubo una serie de casualidades que lo hicieron asistir a una conferencia que dio en Cornell el famoso físico Robert Dicke, quien expuso allí el problema de la planitud.

Dicke impresionó mucho al auditorio expresando numéricamente el problema. Así, mostró que cuando el universo tenía sólo un segundo de edad, el valor de Omega debió estar comprendido entre 0,99999999999999999 y 1,00000000000000001. Si Omega hubiera estado fuera de ese rango, el universo se habría precipitado en el vacío o en un colapso total y no estaríamos aquí para debatir una cuestión filosófica tan fundamental. Ese comentario impresionó de tal manera a Guth, que cambió el rumbo de su carrera y terminó formulando la teoría inflacionaria. ¿A qué se debía un ajuste tan fino de Omega?

Debo aclarar que Dicke no escogió la edad de un segundo arbitrariamente. Hay un supuesto fundamental cuando se hacen cálculos para ilustrar la inestabilidad del universo de geometría plana: que el universo ha venido expandiéndose, pues de lo contrario Omega no se desviaría de uno. Dicke sabía perfectamente que hay pruebas empíricas de que, desde un segundo después del big bang, la expansión del universo se ha desarrollado en un todo de acuerdo con la teoría de Friedmann^[18].

Pero no hay ninguna prueba de que antes de ese segundo haya habido expansión, sólo hay argumentos teóricos. Creemos que se puede aplicar la relatividad general al período anterior, en cuyo caso podemos inferir que el universo debe haberse expandido desde sus comienzos. Aunque no hay pruebas al respecto, pero tampoco tenemos ninguna razón para pensar lo contrario, aceptamos esa extrapolación.

No obstante, sabemos que en un momento del pasado la relatividad general no debió regir: es el tiempo de Planck, instante apenas posterior al inicio del universo, pues se expresa como 0,(42 ceros) 1 segundo. Vivimos en un universo cuántico, sujeto a fluctuaciones aleatorias y, desgraciadamente, no tenemos una teoría cuántica de la gravedad que nos permita prever cómo afectan las fluctuaciones cuánticas a los fenómenos gravitatorios como el movimiento de la Luna y de la Tierra. No obstante, podemos estimar la magnitud de esas fluctuaciones y siempre llegaremos a la misma conclusión: para el cálculo de trayectorias de cohetes y de planetas, son despreciables. No contamos con una teoría cuántica de la gravedad porque, de hecho, no la necesitamos.

Hay, sin embargo, una excepción trágica para la cual sí la necesitamos y es la expansión cosmológica antes del tiempo de Planck. En esos instantes remotos, según la teoría de la relatividad, la expansión es tan veloz que no se pueden desechar las fluctuaciones cuánticas que arrojan las mejores estimaciones con que contamos. Desde luego, no tenemos acceso directo a ese período de la vida del universo, de modo que no podemos decir si las fluctuaciones son importantes. Por otro lado, tampoco tenemos ninguna garantía que nos permita confiar en resultados obtenidos sin el auxilio de una teoría cuántica de la gravedad. A lo largo de este libro, repetiremos este argumento. En lo que respecta a nuestras teorías, la época de Planck, período anterior al tiempo de Planck, es una caja negra y no podemos afirmar nada sobre lo que sucedió en ese turbio pasado.

En particular, no podemos estar seguros de que el universo haya estado en expansión durante esa época. Todo lo que sabemos es que ha venido haciendo equilibrio en la cuerda floja a partir de entonces. Ahora bien, puesto que tenemos razones sólidas para creer que el universo se ha expandido sin cesar desde el tiempo de Planck, cabe preguntar entonces qué valores podía adoptar Omega para que el universo perdurara hasta nuestros días. Los cálculos indican que Omega debió estar comprendido entre 0,(64 nueves) y 1,(63 ceros) 1, es decir, un valor muy próximo a uno.

Creo que ahora resultará evidente por qué digo que hay que ajustar muy precisamente el estado inicial del big bang moviendo a mano las perillas, por así decirlo, para que el resultado tenga sentido. Para empezar, ¿por qué el valor de Omega es tan próximo a uno? ¿Es posible que haya sido exactamente uno? En cualquier caso, ¿por qué? ¿Cuál es el mecanismo que produce valores de Omega tan precisos e impide la catástrofe? El paradigma del big bang no da respuesta a estos interrogantes. Se limita a ofrecer un rango de posibilidades y nos permite elegir un universo con un valor de Omega conveniente, de modo que el modelo resultante describe con increíble exactitud el mundo en que vivimos. Pero todos sabemos que si hubiéramos elegido un modelo apenas distinto, acabaríamos por obtener una monstruosidad.

Lo peor es que nuestra elección no estuvo guiada por ningún principio teórico sino por el mero deseo de que los datos den el resultado que nos conviene. Si hubiéramos elegido el valor de Omega al azar, jamás habríamos arribado al resultado que obtuvimos, pues hacerlo equivaldría a ganar la lotería diez veces seguidas. En consecuencia, los hombres de ciencia empezaron a pensar que los aciertos obtenidos con la teoría del big bang eran algo así como un engaño.

Como el problema del horizonte, el de la planitud reclama conjeturas. Es necesario que los cosmólogos empiecen a preguntarse qué sucedió realmente durante la explosión, en ese primer instante del nacimiento del universo. ¿Qué misterio encierra la época de Planck, inaccesible para la teoría de la relatividad y la cosmología de Friedmann? ¿Acaso esos primeros instantes de vida, ese estado embrionario, entrañaban procesos específicos, una suerte de química hormonal distinta que determinó el valor insólito de esos números misteriosos? ¿Por qué razón ganamos tantas veces seguidas la lotería?

Antes de dejar al lector librado a sus propias cavilaciones sobre estos enigmas, voy a exponer uno más. El tercer enigma del universo en expansión es nada menos que ese ser demoníaco que Einstein desató: la constante cosmológica o Lambda. Fue una mancha en la inmaculada carrera de Einstein que él mismo repudió apenas se confirmaron los descubrimientos de Hubble. Después de tantos traspiés, la constante cosmológica cayó en el descrédito. Tal vez fue el único error grave de la brillante carrera de Einstein. Pero una vez que se descubrió, los hombres de ciencia no hallaron manera de justificar por qué tenía que ser igual a cero.

Recordemos brevemente que Lambda representa la energía del espacio vacío, la potencia gravitatoria de la nada, la puertita especial que Einstein construyó para los gatos menudos. Descubrió que su teoría permitía suponer una energía del vacío no nula siempre que el vacío estuviera sometido a una gran tensión y fuera gravitatoriamente repulsivo, y usó ese hecho para construir un universo estático sin abandonar su teoría. Para conseguirlo, tuvo que definir el valor de Lambda con enorme precisión, de modo que la fuerza de repulsión equilibrara exactamente la atracción gravitatoria habitual. El descubrimiento de Hubble fue la sentencia de muerte del universo estático, pero no acabó con la constante cosmológica. Como Friedmann ya había advertido, sólo un valor artificioso de Lambda correspondía a un universo estático, pues un valor distinto, menos preciso, implica aún un universo en expansión, de modo que los descubrimientos de Hubble no excluyen la constante cosmológica.

Ahora bien, si la energía del vacío no fuera nula, ¿cómo evolucionaría en comparación con otras formas de energía? ¿Se disiparía sin más, a medida que el universo se expandiera? ¿Dominaría a todas las otras especies del universo? Ese es, pues, el tercer enigma del big bang.

Las especies del universo están sometidas a un proceso similar a la selección natural. Algunas desaparecen; otras dominan el panorama y generan períodos y eras glaciales no muy distintos de los experimentados en la Tierra. Hasta ahora, he simplificado la fauna del universo, de modo que el lector tal vez ignora qué quiero decir cuando hablo de otras «especies». Hasta aquí dije solamente que el fluido cosmológico estaba constituido por galaxias, porque ellas son el componente más evidente del universo. Pero no son lo único que hay. Presentaré ahora a los otros personajes de la tragicomedia cósmica.

La figura 5 es una imagen del cúmulo de la constelación de Coma, que contiene más de mil galaxias. En la figura 6 se ve una imagen de la misma región del cielo, pero esta vez tomada con un telescopio sensible a los rayos X, que son indicio cierto de un gas muy caliente; de hecho, de un gas cuya temperatura es de millones de grados. Se puede observar en la imagen que el cúmulo está inmerso en un caldo de gas caliente. Es posible demostrar que ese halo gaseoso contiene la mayor parte de la masa del cúmulo, lo que implica que hay muchas más cosas de las que podemos ver con los ojos.

Experimentos similares demuestran que lo que podemos observar con los telescopios convencionales constituye en realidad una pequeña fracción de la masa del universo. Estamos rodeados por materia oscura que no brilla pero que, sin embargo, podemos «ver» a través de los efectos inequívocos que produce su gravedad. Sólo podemos detectar su peso y, a juzgar por lo que indican las balanzas, la materia oscura constituye la mayor parte del universo. Por consiguiente, conocemos tres especies materiales del universo: las galaxias, el gas caliente y la materia oscura.

Hay más, sin embargo: otro componente que denominamos radiación cósmica de fondo, un mar de microondas que provienen del espacio remoto y que envuelven al vacío en una suerte de baño tibio pues elevan la temperatura de todo en unos 3 grados aproximadamente. Los radioastrónomos Penzias y Wilson descubrieron en la década de 1960 esa radiación de fondo, y al principio creyeron que el efecto provenía de excrementos de paloma depositados en la antena. Limpiaron el aparato concienzudamente, maldiciendo a las palomas que habían hecho nido en la antena. Pero por mucho que limpiaran, no podían eliminar la señal. ¿Tal vez las palomas habían arruinado definitivamente el instrumento? Al cabo de un tiempo, se dieron cuenta de que habían detectado algo mucho más importante, el eco de otro componente del universo, un fluido cósmico de radiación que debía agregarse al fluido de galaxias, gas caliente y materia oscura.

Pues bien, hasta donde sabemos, esos son los ingredientes básicos del big bang^[19]. La pregunta que debemos formular es la siguiente: ¿cómo los afecta la expansión? La respuesta es muy sencilla. Lo que sucede depende de si el componente en cuestión tiene presión interna o no. Ya hemos visto que la presión y la tensión pueden afectar la potencia gravitatoria de un objeto. De hecho, si se comprime un objeto lo suficiente, ese objeto puede incluso producir un efecto de repulsión gravitatoria, como ocurre en el caso de la constante cosmológica, el artilugio que pergeñó Einstein para obtener un universo estático a partir de la reacia teoría general de la relatividad. Ahora sabemos que la presión es el factor que determina si el universo en expansión podrá sobrevivir o no. De modo que tenemos un panorama complejo: en un rincón, las galaxias y la materia oscura; en otro, la radiación cósmica, y en un tercero, agazapada amenazadoramente, la constante cosmológica.

Empecemos por el fluido de galaxias, carente de presión, pues la presión se debe a movimientos aleatorios de las moléculas. La presión atmosférica, por ejemplo, es el resultado de veloces movimientos moleculares que causan el choque de moléculas contra cualquier superficie y generan así presión. Pero no hay movimientos de este tipo en las galaxias, y si los hay, son despreciables. En líneas generales, las galaxias están en su lugar y carecen de presión. Utilizando un giro algo poético, los cosmólogos denominan «polvo cósmico» a ese fluido desprovisto de presión.

A medida que el universo se expande, las galaxias carentes de presión se apartan o, mejor dicho, siguen incrustadas en un espacio que se expande y genera cada vez más lugar entre ellas. Si pudiéramos pintar de rojo una región del universo, la mancha roja aumentaría de tamaño con la expansión, pero el número de galaxias contenido en ella no cambiaría. La tasa de dilución de cualquier fluido similar al polvo cósmico carente de presión, que está sometido a expansión, es idéntica a la tasa de aumento del volumen. Por lo que sabemos hasta ahora, la materia oscura también se comporta como un fluido de polvo, de modo que su evolución con la expansión del universo coincide con la de las galaxias; la materia oscura también se diluye con una tasa idéntica a la del incremento de volumen.

Con la radiación ocurre algo distinto, porque está constituida por fotones, partículas de luz que naturalmente se mueven a la máxima velocidad posible en el universo. Por esa razón, un fluido de radiación como el del fondo de microondas cósmico tiene una presión bastante grande. ¿Cómo afecta este hecho a la evolución del fluido cuando está sometido a la expansión cósmica?

A medida que el universo se expande, los fotones están cada vez más dispersos pero también ejercen presión sobre el espacio en expansión. Es como si hicieran un trabajo y contribuyeran a la expansión utilizando parte de su energía. Como dijimos antes, mientras el universo se expande, una determinada región de él pintada de rojo también se expande, pero sigue conteniendo el mismo número de fotones. Sin embargo, cada fotón se torna más débil pues va agotando su energía en el aporte que hace a la expansión. Por consiguiente, un fluido de radiación se diluye con la expansión mucho más rápidamente que el polvo, por dos razones: por la expansión del volumen y por la reducción adicional de energía que implica su contribución a la expansión.

Este hecho tiene consecuencias de suma importancia para la historia del universo. Si la radiación se diluye más rápidamente que la materia, debió existir en las primeras etapas del universo una radiación muy densa y muy caliente. De hecho, si una especie se diluye más velozmente que otra, debe esfumarse en las fases tardías y debió predominar en las primeras etapas. En otras palabras, la radiación cósmica es algo así como un dinosaurio: algo que está prácticamente en extinción pero que imperaba en el universo en épocas arcaicas. Así, el descubrimiento de la radiación cósmica derivó en un modelo particular del big bang denominado hoy hot big bang, que entraña un universo en expansión con un pasado abrasador en el cual predominaban los fotones de alta energía que formaban un mar de radiación sumamente caliente.

Lo dicho hasta aquí se refiere a los ingredientes rutinarios del universo que integran la versión más apetecible del big bang. Pero ¿qué sucede con la supervivencia de los más aptos si agregamos unas gotas de constante cosmológica? ¿Qué destino le toca a ese animal hipotético cuando se lo somete a la expansión?

Recordemos que la energía del vacío ya está sometida a una tensión extrema, de suerte que se opone a la expansión al resistirse a una tensión mayor. De este hecho se infiere que, al contrario de lo que sucede con la radiación, la expansión cósmica debe transferir energía a la constante cosmológica a medida que estira esa especie de banda de goma que es Lambda, y la obliga a acumular cada vez más tensión. En consecuencia, la expansión tiene un efecto doble sobre Lambda: por un lado, diluye su energía y, por el otro, se opone a la tensión transfiriéndole energía. La disminución de la energía debida a la expansión del volumen y la acumulación de energía en forma de tensión son dos efectos opuestos que entrañan un resultado peculiar. La densidad de energía implícita en la constante cosmológica es la misma en todo momento y no se ve afectada por la expansión del universo: sometida a expansión, ¡su densidad energética sigue siendo la misma!

Se trata de un hecho de consecuencias espectaculares pues, si en un instante determinado de la vida del universo hay el menor vestigio de energía del vacío, entonces, a medida que el universo se expande, y se diluyen el polvo cósmico y la radiación, Lambda predomina cada vez más. Pero el predominio del vacío puede acarrear una catástrofe, es decir, un universo muy distinto del que conocemos. La oscuridad invadiría los cielos y nuestra galaxia se encontraría aislada; además, no se registraría ninguna radiación cósmica. ¿Por qué razón no hemos llegado a esa situación?

Hagamos lo mismo que hicimos antes y hablemos concretamente de cifras. Consideremos en primer lugar el universo al cabo de un segundo de existencia. Se puede demostrar que el porcentaje de energía del vacío en el universo debe ser inferior al 0,(34 ceros) 1 por ciento para que Lambda no haya dominado la situación hace ya mucho tiempo. Si imponemos más restricciones y suponemos que el universo se está expandiendo desde el tiempo de Planck, entonces el aporte inicial de la energía del vacío tiene que haber sido inferior a 0,(120 ceros) 1 para que las cosas sean como son.

Esto implica transitar por otra cuerda floja, mucho más peligrosa todavía.

Los enigmas del big bang son muy incómodos, de modo que ya en la década de 1960 los cosmólogos luchaban por encontrarles solución, pero todas las que hallaron tenían fallas. Uno de los intentos más interesantes tal vez fue el de Yakov Zeldovich, cosmólogo ruso cuya vida tiene muchos puntos de contacto con la de Friedmann. Los seis años de escuela secundaria fueron toda su educación formal, circunstancia que quizás explique su extraordinaria imaginación y creatividad. Fue en gran medida un autodidacta, pero, aun cuando no asistió jamás a la universidad, recibió el título de doctor a la edad de 22 años.

A Zeldovich, como a Friedmann, le faltó lastre^[20]. Tuvo tantas ideas innovadoras en el campo de la cosmología que a veces los investigadores creen que hubo varios científicos con el mismo nombre. De hecho, para distinguir las diversas fórmulas que llevan su nombre, se les agrega el de algún otro científico occidental que arribó al mismo resultado varios años más tarde. Pues bien, Zeldovich propuso el modelo de universo oscilante o pulsante como solución de los enigmas del big bang.

Veamos en qué consiste su receta. Se toma primero un modelo esférico o cerrado y se le permite expandirse después del big bang. Sabemos que ese modelo termina por cambiar de rumbo e implosiona. Según la teoría general de la relatividad, su estado final debe ser el big crunch. Pero también sabemos que, a medida que el universo avanza hacia su colapso, adquiere una velocidad de contracción que es un reflejo exacto de la velocidad de expansión que tuvo en la época de Planck. En rigor, el universo debe ingresar en un período similar, en el cual entran en juego efectos gravitatorios cuánticos desconocidos. La única diferencia es que, en esta historia, el universo se contrae en lugar de expandirse. Los cosmólogos se preguntan si esos efectos gravitatorios cuánticos no pueden transformar el colapso en un nuevo big bang, esto es, si no habrá una especie de «rebote» cósmico.

El universo oscilante ha recibido también el nombre de universo fénix, pues renacería de las cenizas del colapso mediante una nueva explosión, cumpliendo así un ciclo infinito. Zeldovich pudo probar que cada nuevo ciclo debía ser mayor (más largo) que el anterior^[21] (véase la figura 7). A partir de allí, intentó resolver los enigmas del big bang utilizando ese modelo.

No hay duda de que los misterios que encierra el big bang son deslumbrantes y riesgosos. Reclaman una física nueva, piden a gritos una cosmología distinta pero, sin embargo, no dan ningún indicio de una solución posible. Es muy fácil que, frente a ellos, la gente más inteligente parezca idiota. Recuerdo una de aquellas reuniones itinerantes sobre cosmología en la cual Neil Turok, uno de los principales adversarios de la teoría inflacionaria, mantuvo una acalorada discusión con alguien que sostenía que la inflación era la única solución conocida para el problema del horizonte y el de la planitud. Neil no se calla fácilmente, y retrucó de inmediato que eso no era cierto, que ahí mismo podía dar muchas explicaciones alternativas. Supongamos, dijo, que mientras el universo llegaba a ser «algo», empezaba a actuar algún principio que sólo garantizaba la existencia de un universo tan simétrico como fuera posible. Tal principio implicaría por fuerza un universo homogéneo y plano, ¿no es verdad? Pues bien, esa es una solución de los problemas de la homogeneidad y la planitud.

Hmmm… Siempre tuve la sensación de que el uso excesivo de la palabra «algo» permite que cualquiera resuelva todo tipo de problemas, incluso los insolubles. Pero aquí hay un error más evidente aún. Apenas Neil había terminado de hablar, Mark Hindmarsh, medio adormilado, desde unos asientos más allá, dijo súbitamente: «Bueno, en ese caso, ¿el universo no sería el espacio-tiempo de Minkowski?».

Hubo unos momentos de silencio mientras todos digeríamos ese nuevo comentario… y luego estallaron las carcajadas. Para cualquiera que domine las matemáticas elementales, lo que había dicho Hindmarsh era evidente: el espacio-tiempo de Minkowski, el espacio vacío carente de efectos gravitatorios, era el modelo más simétrico con que contábamos. Está tan vacío que su aspecto es idéntico en toda dirección, espacial o temporal. Desgraciadamente, ese «algo» que había mencionado Neil entrañaba un resultado manifiestamente erróneo —que deberíamos vivir en un mundo sin gravedad— en lugar de resolver cualquier problema cosmológico.

Todos se rieron de esa equivocada tentativa de resolver el problema del horizonte y el de la planitud, pero más tarde pensé que al menos Neil había intentado responder. El sello distintivo de los buenos problemas es su frustrante sencillez, frustrante porque apenas uno piensa que podrá resolverlos y abre la boca para proponer una solución, dice tonterías por más inteligente que sea.

Sin embargo, Neil se había equivocado en otra cosa. Para ser justos, y a pesar de todo lo que se dijera en el momento, a mediados de la década de 1990 había una sola respuesta para todos los enigmas que planteaba el big bang: la teoría del universo inflacionario de Alan Guth.