16. Biogeochemical Fluxes in Terrestrial Ecosystems

16.1.1 Water Budget at Ecosystem Scale

Water flows through ecosystems, is stored only to a small degree in the soil profile, and leaves the ecosystem, either as water or water vapour. Thus, it is more appropriate to speak of a water budgetthan of a water cycle at the ecosystem scale. The ecosystem gains water via precipitation (rain, snow, fog, dew, rime and hail, adding up to total precipitation). Water reaches the ground below a plant canopy as throughfall or as stemflow (Fig. 16.1). Throughfall is defined as the sum of precipitation reaching the soil, that is, precipitation that either falls through canopy gaps or is intercepted by foliage, and what is not evaporated from these surfaces drips down leaves or needles (leaf drip). Throughfall is larger in open canopies and smaller in dense canopies because foliage, branches and stems intercept precipitation water (interception), of which a fraction evaporates and never reaches the ground. Interception by deciduous forests is typically much smaller than that by coniferous and evergreen forests (15–25% vs. 27–66%, respectively) (Fig. 16.1) owing to their clumped needle arrangements and long foliage presence throughout the year. Stemflow is higher for trees with smooth barks and a funnel-shaped crown architecture (such as beech, Fagus spp.) compared to trees with rough barks and irregularly shaped crowns (such as oak, Quercus spp.). Thus, throughfall is the difference between bulk precipitation (measured above the canopy or in the open), stemflow and interception (evaporation from plant surfaces), measured by rainfall collectors placed on the ground, stratified by canopy cover (accounting for gaps as well). The structure of the vegetation may modify the water input, for example, by “stripping” water from ground-reaching clouds (i.e. fog) via increased above-ground surface area that can intercept fog droplets. Examples are the laurel forests in Tenerife, which depend to a large extent on water harvested from clouds, or the tropical montane cloud forests in Puerto Rico. In Sequoia sempervirens (coastal redwood) forests in Northern California, 34% of the annual water input is due to fog drip, contributing 19% of transpired water during summer for large trees (Dawson 1998). Depending on how bulk precipitation is defined or where it is measured (above the canopy or in the open over low vegetation), interception can lead to water losses (relative to total precipitation measured above the canopy) or to water gains (relative to precipitation measured over low vegetation, which does not strip out fog). Moreover, ecosystems lose water by run-off and infiltration into the ground, contributing to seepage into the groundwater or river discharge, but also as water vapour lost to the atmosphere via evaporation from wet surfaces and via transpiration from plant foliage (Chaps. 9 and 10).

The hydrological balance can be described as follows:

(16.1)

where P denotes total precipitation, E evapotranspiration, F run-off and seepage, and ΔS change in soil water storage. Often, ΔS is considered zero and therefore omitted from this equation (Eq. 10.​1, Chap. 10).

The water budget is positive if P > E + F + ΔS, for example, in areas with high rainfall. It is negative if P < E + F + ΔS, for example, when P is completely used by E or if E is fed by supplies other than P, such as irrigation. Spatially as well as temporally, the hydrological budget is highly variable, but on average, as much as 60% of total terrestrial precipitation is returned to the atmosphere by ecosystem evapotranspiration (Oki and Kanae 2006; Williams et al. 2012) (Chap. 10).

Understanding the partitioning of precipitation into evapotranspiration and run-off/seepage processes is one of the challenges in ecohydrology, since not only climate but also land cover (e.g. forest, grassland, cropland, urban area) and land use (e.g. crop rotation, intensive agriculture, extensive grazing), and thus terrestrial ecosystems, strongly affect this partitioning. Using the concept of Budyko (1974) (Fig. 16.2), one can separate the climatic radiative effect (driven by net radiation) from the land surface evaporative effect (driven by precipitation) and, thus, study the impacts of ecosystem characteristics. This makes it possible to compare effects for different vegetation and ecosystem types, but also to study impacts of inter- and intraseasonal variations. Plotting the ratio of mean annual (actual) evapotranspiration E and total precipitation P (E/P; also called the evaporative index, EI) versus the ratio of potential evapotranspiration E _p and total precipitation P (E _p/P; also called the dryness index, DI) results in the Budyko space. In theory, two profound upper limits can be hypothesised: the supply limit where evapotranspiration equals precipitation (horizontal line in Fig. 16.2) and the demand limit where actual evapotranspiration (controlled by meteorological conditions and ecophysiology) equals potential evapotranspiration E _p (controlled only by meteorological conditions). Here, E _p is defined as evapotranspiration by an ecosystem fully supplied with water to fulfil meteorological demands (calculated by Penman-Monteith; see following discussion). However, there exist many different definitions of E _p, for example, evaporation from open water, and many ways to calculate E _p, for example, only taking temperature into account, adding wind speed or vapour pressure deficits. Here, exceeding E _p/P = 1 indicates an ecosystem water deficit at annual time scales, while the term 1 − E/P quantifies the annual run-off or seepage in any given ecosystem.

Based on 167 ecosystem flux sites (Sect. 14.​1, Chap. 14) and 764 site-years, about 93% of all the sites were found to be at or below the demand and supply limits (Fig. 16.2b, c). The remaining 7% were outside the theoretical limits (e.g. more water used for evapotranspiration than supplied via precipitation), most likely owing to measurement biases (Chap. 14) and changes in soil water storage (which is assumed to be zero in the Budyko concept) (Williams et al. 2012). About 62% of the variation in E/P across sites, that is, the fraction of precipitation returned to the atmosphere by evapotranspiration, was driven by net radiation (energy-driven), and an additional 13% was explained by climate and vegetation types (physiology-driven). This showed that despite the dominance of radiative controls on E, further vegetation type-related controls on E must be included in models of water fluxes. Interestingly, grasslands had on average a higher E/P (65%) than forest ecosystems: E/P of 56% for deciduous broadleaf forests (DBF) and 63% for evergreen needleleaf forests (ENF) (Fig. 16.2c), quite similar to croplands (E/P of 69%). This is consistent with measured leaf transpiration rates (Larcher 2003) and various strategies observed for grasses vs. trees on how to deal with water stress (Chap. 10, Fig. 10.​16). However, this contrasts with the better coupling of forests (leading to higher E), with trees having deeper root systems and, thus, access to deeper soil depths (with more water; but Chap. 10, Fig. 10.​12) and maybe higher leaf area index (LAI) than grasslands.

16.1.2 Water Uptake of Trees

An alternative approach is to use stable isotopes of water, either oxygen or hydrogen isotope ratios (δ¹⁸O or δ²H, respectively), to determine the soil water source or the rooting depth of water uptake. However, since precipitation changes its isotopic signature seasonally (Fig. 16.3), due to changes in temperature, atmospheric water vapour pressure and origin of air masses (Gat 1996), frequent sampling and hydrological modelling of the isotope ratios in soil water will best account for the biogeochemical variations of this important plant resource. Since no isotope fractionation takes place during root water uptake, isotope ratios in xylem water reflect the total soil water uptake of a plant. Non-transpiring tissues need to be sampled for these measurements, that is, root collars (Barnard et al. 2006), branches or twigs (Ehleringer et al. 2000), to avoid evaporative enrichment: During evaporation, lighter water molecules evaporate faster, so the remaining water pool becomes enriched in the heavier isotopes and no longer reflects the original water source. In a mixed forest, oxygen stable isotope ratios in soil water follow the precipitation inputs with some time lags, particularly in deeper soil layers, while the isotopic signatures in xylem water of temperate tree species show a pronounced seasonal course, but species also differ (Fig. 16.3).

Mixing of existing water pools in the soil profile with rain infiltrating into the soil depends on the soil structure, soil moisture content and precipitation regime. Based on these variables, the mean residence time of water at a particular soil depth can be modelled (Fig. 16.4). Such models account for preferential flow through macro pores (e.g. earthworm casts, root channels, cracks), which can lead to very high flow rates (within days). The “age” of water is higher at greater depths in the soil profile, and mean residence times can reach more than 1 year at a depth of 0.8 m. At more shallow depths, the impact of current precipitation is prevalent, and water pools mix over a period of about a month. Combining this information with the isotopic signatures of xylem water shows that P. abies takes up water from more shallow soil depths, while F. sylvatica, A. pseudoplatanus and F. excelsior take up water from deeper horizons. Since soil water is the ultimate pool to supply water for tree transpiration, susceptibility to short dry spells or droughts will also differ among these species (all other drivers for evapotranspiration being equal) (Sect. 16.1.3).

16.1.3 Evapotranspiration at Canopy and Ecosystem Scales

Evapotranspiration of ecosystems is both energy-driven and physiology-driven, as shown in the preceding section. Different processes are involved: transpiration via stomata and evaporation from surfaces. Ecosystem water vapour fluxes are thus composite fluxes since evapotranspiration can also originate from different surfaces: from soils and from vegetation (wet leaves, branches and stems). Sometimes a different partitioning method is used, canopy vs. subcanopy layer, with the latter including soil and understorey vegetation. This means that attention needs to be paid to distinguishing different units (water vapour flux in mmol per m² leaf area or per m² ground area) and different spatial scales (leaf, soil, canopy, ecosystem; for leaf transpiration, Chap. 10).

The energy budget equation (also Eq. 9.​4 in Chap. 9)

(16.2)

links the turbulent fluxes of latent (λE) and sensible heat (H = ρ c _p G _H ΔT) (Chap. 9) to net radiation R _n, which, ultimately, is the energy input from the Sun that drives both turbulent fluxes and soil heat flux G. The flux of water from the ecosystem depends primarily on the energy that is available for vaporizing water, but H and λE are also substantially affected by turbulent conditions.

Since energy and water vapour fluxes are tightly coupled, evapotranspiration can be expressed as water vapour flux E in mm year⁻¹ or mmol m⁻² s⁻¹ (or any other time unit), but also as latent heat flux λE in W m⁻² (Fig. 16.5). This has the advantage that many energy-related and plant-related factors can be considered, such as

• Available solar energy for supplying the energy needed for the vaporisation of water.

• Precipitation input, water vapour pressure deficit of air, soil moisture, soil structure, supplying water and controlling water uptake.

• Roughness of surface (soil, canopy, ecosystem), which determines the coupling of the canopy to the atmosphere.

• Ecosystem structure, for example, fraction of bare soil, stand architecture, LAI, affecting energy budget of the ecosystem.

• Plant structural variables such as leaf area, and the leaf angle, affecting the absorption of incoming radiation.

• Leaf ecophysiology such as leaf conductance

• Spectral characteristics of surfaces, which determine the sensible heat flux.

The leaf-scale equation to describe leaf transpiration E _L (Chap. 10, Eq. 10.​17) only accounted for two of these factors, namely stomatal conductance g _S and water vapour pressure deficit between leaf and air D _L. However, D _L is in turn dependent on E _L since higher transpiration rates humidify the air around the leaf. To account for this feedback (and others), the so-called Penman-Monteith equation (Eq. 16.3) describes evapotranspiration as energy flux, that is, as latent heat flux λE (in W m⁻²) (Monteith 1965). The derivation of the equation is explained in Jones (2014). The latent heat flux of a terrestrial ecosystem depends on net radiation R _n (above canopy level) (Fig. 16.6), soil heat flux G, with R _n – G also being called available energy, water vapour pressure deficit of air D, and the total conductances for water vapour G _w and for sensible heat G _H (uppercase G depicts ecosystem level compared to g at the leaf level):

(16.3)

where the coefficient s (in Pa K⁻¹) describes the change in saturation vapour pressure with temperature, D is the saturation vapour pressure (in Pa), ρ is the density of air (1.204 kg m⁻³ at sea level), c _p denotes the specific heat capacity of air (1012 J kg⁻¹ K⁻¹), and γ (Pa K⁻¹) denotes the psychrometric constant (66.1 Pa K⁻¹) (Chap. 9). Both conductances G _W and G _H (in m s⁻¹) describe the entire pathway between the leaves and bulk air, including stomatal, cuticular and boundary layer components at the ecosystem level. The soil heat flux G is rather small, typically 2% of R _n in dense canopies, increasing to about 30% in very sparse canopies.

Under completely turbulent transport conditions for heat and water vapour in the boundary layer, G _H and G _W are similar and can be replaced by a boundary layer conductance (G _a, where a represents the atmosphere) and the surface conductance of the ecosystem (G _s). G _a describes the conductance between the free atmosphere and the surface(s) under study, that is, the soil surface and the canopy (leaf and stem surfaces), while G _s stands for the conductance out of the soil and into or out of the stomata of the foliage. Thus, for the sensible heat transfer H from a leaf or needle to the atmosphere, this transfer starts at the outer leaf surface and G _H = G _a (which can also be expressed using resistance r instead of conductance: G _H = 1/r _H = 1/r _a = G _a). However, for the latent heat transfer λE from a leaf or needle and the soil surface to the atmosphere (water vapour leaving the foliage via evapotranspiration and the soil via evaporation), this transfer starts inside the leaf and from the soil, so G _W = 1/r _w = 1/(r _a + r _s). Replacing G _H/G _w in Eq. (16.3) with (1 + G _a/G _s), and recalling that G _a = 1/r _a and G _s = 1/r _s, Eq. (16.3) can be expressed as

(16.4)

Ecosystem-scale evapotranspiration (E) (Fig. 16.6) can be partitioned into canopy evapotranspiration (E _c) and soil evaporation (E _g) (following discussion) with

(16.5)

If no measurements are available (Sect. 14.​1 in Chap. 14), E _c can be scaled up from leaf transpiration (E _L) using a “big-leaf model”, assuming all leaves in the canopy behave the same, as a single leaf:

(16.6)

However, to be closer to reality, currently also “two-leaf models” are used, which account for different behaviours of sunlit and shaded foliage within a canopy (Liu et al. 1997) (Chap. 15). Those interested in mathematics should read the work by Raupach and Finnigan (1988) with the remarkable title “Single-layer models of evaporation from plant canopies are incorrect but useful, whereas multi-layer models are correct but useless”. Fortunately, since this publication, science and particularly model development have progressed, and optimisation theory and remote sensing approaches are used to describe canopies in more complex ways (e.g. Buckley et al. 2013; Peltoniemi et al. 2012).

Similarly, surface conductance G _s can be partitioned into

(16.7)

with G _c = canopy conductance and G _g = soil conductance. The canopy conductance (G _c) is estimated by the conductance in the boundary layers around the leaves and the stomatal conductance.

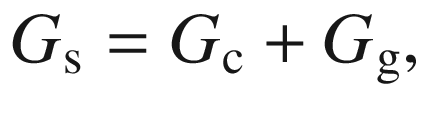
Surface conductance G _s approaches canopy conductance G _c when the leaf area increases because soil evaporation becomes negligible in dense canopies (LAI > 3). It should also be noted that G _s is not equal to leaf conductance g _L because it includes not only the surfaces of vegetation in the ecosystem, but also the surface of the soil (Fig. 16.6) (Schulze et al. 1994).

Using the big leaf model, canopy conductance G _c can be approximated as

(16.8)

Using a more stratified leaf model with i canopy strata, canopy conductance G _c can be approximated as

(16.9)

with = mean leaf conductance in stratum i and LA_i = leaf area in stratum i.

Because carbon dioxide and water vapour fluxes of a canopy are tightly coupled, we included carbon dioxide assimilation of the canopy A _c in Fig. 16.6 as well. A _c is determined by leaf net photosynthesis, which is controlled by the CO₂ gradient between the ambient air and the leaf intracellular air space (= c _a – c _i), the leaf conductance g _L, and foliar nitrogen nutrition, scaled up by canopy LAI (modulated by incoming radiation and leaf arrangement, for example, leaf angles, clumped needles and so forth).

Soil evaporation is dependent on the available energy at the soil surface (Fig. 16.6), the soil moisture available in the soil and D above the soil surface (for details, Seneviratne et al. 2010). The significance of soil evaporation becomes obvious when the maximum canopy conductance, the component of surface conductance related to the plant canopy, is plotted against the LAI (Fig. 16.7). As given by Eq. (16.6), both canopy and surface conductances are affected by different maximum stomatal and, hence, leaf conductances (g _Lmax). Canopy conductance increases with LAI and becomes saturated at about LAI 5 (for g _Lmax 4 mm s⁻¹) and at about LAI 9 (for g _Lmax 12 mm s⁻¹). In contrast, surface conductance behaves somewhat differently. With decreasing LAI, free evaporation from the wet soil surface becomes more important. At LAI 2 (at low g _Lmax), evaporation from the soil is as large as that from the canopy, as long as the soil surface is wet. For LAI < 1, surface conductance increases again because the water budget is determined by evaporation from the soil (Greenwood et al. 1992).

All energy components show a pronounced diel course on a cloudless day, driven by incident solar radiation (Fig. 16.8a). The grassland actively transpires during the day, so the latent heat flux consumes the largest share of the net radiation R _n. It takes about 2 h for the vegetation to increase transpiration with slowly increasing air temperatures and, thus, changes in water vapour deficit (Fig. 16.8b). The soil heat flux is the smallest term in the energy budget and shows the least diel variability, with a slightly shifted peak 1 h after the peaks for latent and sensible heat fluxes (Chap. 9). The soil temperatures lag behind air temperature: peak soil temperatures occur later for greater depths. During the day, air and soil surface temperatures can be very similar. Canopy surface temperatures are slightly lower than air temperatures during the night owing to longwave radiation losses but are much higher during the day. Although net radiation is dissipated in latent and sensible heat fluxes and ground heat flux, the transpirational cooling is not enough to cool the leaf surfaces below air temperatures (Sect. 9.​4).

Depending on the overall environmental conditions, sensible and latent heat fluxes of different ecosystem types can account for a similar fraction of dissipated incoming energy (Table 16.1): this is often the case for grasslands and evergreen forests. However, deciduous forests and croplands often show a higher fraction of energy dissipated as latent heat, that is, evapotranspiration, compared to sensible heat. This results in a typical low Bowen ratio (β), that is, the ratio of sensible to latent heat fluxes (Eq. 16.10), for croplands and deciduous forests, but higher ratios for evergreen forests. Grasslands, owing to their highly variable soil water supply, also have highly variable Bowen ratios:

(16.10)

Table 16.1

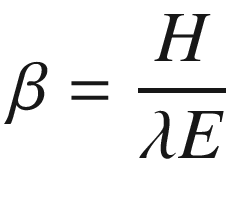
Comparison of albedo, sensible and latent heat fluxes as well as Bowen ratios across ecosystem types

	Evergreen forests	Deciduous forest	Grasslands	Croplands
Albedo (%)	10 ± 2	13 ± 1	20 ± 2	17 ± 2
Sensible heat H (%)	44 ± 10	25 ± 7	44 ± 15	19 ± 4
Latent heat λE (%)	46 ± 10	62 ± 7	46 ± 15	64 ± 4
Bowen ratio (H/λE)	0.5 to 1	0.25 to 0.5	highly variable	0.25 to 0.5

Means ±1 standard deviation are given based on multiple studies. Albedo is calculated based on incoming radiation. Data from Wilson et al. (2002), Cescatti et al. (2012)

It is interesting to note that the Bowen ratio increases when temperate ecosystems are converted to urban settlements, approaching values similar to deserts. In contrast, Bowen ratios decrease with irrigation, indicating higher water vapour and lower sensible heat fluxes due to evaporative cooling. Another useful ratio describes the fraction of available energy (R _n – G) used for latent heat λE, thus λE/(R _n – G), which is more intuitive and often more useful than the Bowen ratio.

16.1.4 Imposed and Equilibrium Evapotranspiration of Leaves and Canopies

(16.11a)

(16.11b)

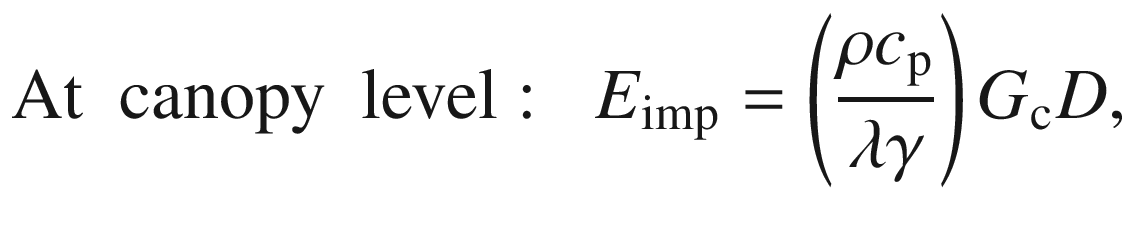
• where g _L or G _c describes the corresponding physiological conductance of the leaf or the canopy. Owing to the full coupling, the conditions of the atmosphere are “forced or imposed” on the leaf or canopy, so that evapotranspiration is linearly related to conductance and water vapour deficit (which in turn is affected by conductance).

1. 2.

   The leaf or canopy is not well coupled to the atmosphere. This is the case for large leaves, very short vegetation (short lawn), conditions with still air (no turbulence) or within a greenhouse. Here, the boundary layer around the evaporating surfaces is very large, so the boundary layer conductance is very small, and the transfer of heat and mass (water vapour) is very poor. This means that the energy supply R _n dominates evapotranspiration. Thus, Eq. (16.4) is reduced to describe equilibrium evaporation E _eq:

    

(16.12)

For both leaf and canopy evapotranspiration, water vapour loss is in equilibrium with the available net incoming radiation R _n, independent of leaf or canopy conductance. Such conditions exist for example on an even lawn. Leaf stomata may be wide open, but the canopy will lose little water because the transport of water vapour through the boundary layer does not take place. Thus, evapotranspiration saturates the boundary layer, and D will approach zero. Water vapour transport to the atmosphere is only enhanced if the temperature of the surface rises as a consequence of radiation. For large crop areas, actual evapotranspiration is about 26% larger than E _eq based on Eq. (16.12), so a factor 1.26 is introduced into the nominator (Priestley–Taylor coefficient) to increase the estimated evapotranspiration rate E _eq. The discrepancy arises because turbulent mixing in and above the field prevents the boundary layer from becoming fully saturated, so D is larger than zero.

Since E _eq is purely energy-driven, one can also interpret E _eq as potential evaporation (no physiological effect via transpiration). Physically, E _eq represents simply the water vapour flux from an open water surface that has the same surface temperature as a leaf or a canopy fully supplied with water, under conditions when the atmosphere is fully saturated with water vapour (D = 0). However, there are many different ways to calculate potential evaporation (for details, see climatology textbooks).

Under natural conditions, both extreme cases can happen, but usually a mixture of evapotranspiration occurs, driven by radiation inputs (E _eq) and imposed by the combination of atmospheric water vapour saturation deficit and leaf or canopy conductance (E _imp):

(16.13)

where Ω is the decoupling factor, which quantifies the connection of the vegetation to the atmosphere. Ω can vary between 0 (perfect coupling) and 1 (complete isolation).

(16.14a)

(16.14b)

The sensitivity with which evapotranspiration reacts to changes in stomatal closure (dE/E)/(dg _L/g _L) or (dE/E)/(dG _c/G _c) is directly determined by Ω:

(16.15a)

(16.15b)

The aforementioned relations are very important in understanding water vapour loss from plant canopies. Under certain conditions, the characteristics of the vegetation are more important than stomatal regulation. A branch standing out from a wind-swept canopy of a forest experiences different evaporative conditions than other leaves protected in the canopy. The decoupling factor Ω decreases (coupling increases) with an increasing height of vegetation (Fig. 16.9) and increases with smaller leaves. However, this does not explain how and to what extent evapotranspiration takes place, because at constant Ω, evapotranspiration is dependent on radiation, the water vapour saturation deficit and the corresponding conductance.

Decoupling can also be achieved by specific morphological adaptations at the leaf level, which reduce the boundary layer around the leaves. For example, leaf petioles with an elliptic, flattened cross section lead to leaf movements even at very low wind speeds. The fast-growing species Populus tremula has “shivering” leaves (Latin name tremulus = trembling) already in light breezes, decreasing the leaf boundary layer, thus increasing the boundary layer and leaf conductances and, in turn, leaf gas exchange (Sect. 9.​3 in Chap. 9). Thus, E _imp dominates leaf and canopy E, being strongly driven by g _L and D (Eq. 16.11a). Growing on moist soils, this species can afford high transpirational losses due to high leaf conductances to enhance CO₂ uptake and, thus, growth.

16.1.5 Responses of Terrestrial Ecosystems to Drought

Biogeochemical processes in ecosystems react to changes in environmental conditions just like physiological processes in leaves and individual plants. Using the appropriate measurement techniques for the scale under study, here the ecosystem scale (Box 16.1), one can quantify these changes and compare magnitudes of process rates and responses of different ecosystem types to the same driver. Moreover, one can study the interactions of different biogeochemical processes, like evapotranspiration (ET) and gross primary production (GPP). The ratio of GPP to ET (sometimes called ecosystem water-use efficiency) also provides insights into different survival strategies, that is, how the ecosystem reacts to environmental stress such as a severe drought. This is of particular interest since extreme events like droughts are expected to increase with anthropogenic climate change (Chap. 21).

Using the eddy covariance technique to measure ecosystem CO₂ and water vapour fluxes (Chap. 14), it was shown that during a year with a severe spring drought (2011), forests—in contrast to grasslands—increased GPP relative to ET compared to the (representative) year before (2010). All sites studied (subset of two shown in Fig. 16.10) showed an earlier start of the season, so GPP could be maintained also in 2011 (Wolf et al. 2013). However, owing to the water shortage in spring 2011, forests reduced their water loss (via stomatal regulation of transpiration), which led to increased GPP/ET ratios (steeper slope in Fig. 16.10). This is in stark contrast to the behaviour of grasslands: no change in water vapour losses was observed, the slopes of GPP over ET did not change, so grasslands showed the same GPP relative to ET in both years. Thus, susceptibility to drought strongly differs between grasslands and forests, probably owing to different evolutionary adaptation strategies (meristems of grasses are close to the ground, not at great height, ability of frequent regrowth after foliage loss).

These different behaviours of grasslands and forests were supported by combining flux measurements and models at the next larger scale, the region. For the combined heatwave and drought in summer 2006 across Europe, grasslands showed much higher evapotranspiration rates at the beginning of the heatwave and drought than forests (Teuling et al. 2010). This resulted in a cooling of the atmosphere over grasslands but a heating over forests. Only longer into the extreme event, when grasslands started to wilt and die off, but forests still continued to transpire (although at a low rate), did this result in a cooling of the atmosphere over forests at later stages of the heatwave and drought. This shows how different ecosystems differ in their responses and feedbacks to changing environmental conditions, in this case to the atmosphere (Chap. 23).

16.2.1 Carbon Pools and Fluxes in Terrestrial Ecosystems

Carbon enters terrestrial ecosystems as atmospheric carbon dioxide (CO₂) during gross primary production (Fig. 16.11). It is allocated as carbohydrates within plants and used to grow plant tissues and for storage (Chap. 12), but also to fuel ecosystem respiration, both from autotrophic plants and heterotrophic microbial organisms and soil fauna. Because of these two large ecosystem CO₂ fluxes (photosynthesis and respiration), there is a close coupling between the atmosphere and the biosphere, mediated by a turbulent exchange of air masses above and within the ecosystem. When plant tissues senesce and become litter, decomposition of this dead organic matter (necromass) sets in. Decomposition by soil fauna and microorganisms includes decay, that is, the biotic breakdown of organic matter, and mineralisation, that is, the release of inorganic nutrients, but also CH₄ and CO₂ (thus heterotrophic respiration). Stabilisation of organic matter, that is, the formation and protection of soil organic matter (SOM) (Sect. 20.​4 in Chap. 20), contributes to carbon sequestration. Thus, the largest carbon pool in ecosystems is often in the soil (except in tropical forests). Additional losses occur during leaching of DOC and dissolved inorganic carbon (DIC) from the soil, but also during erosion. During fires and with harvests, large amounts of carbon are removed from ecosystems, although both fire and harvest residues also make large contributions to SOM. Depending on fire frequencies and the degree of ecosystem management, vegetation degeneration, soil degradation and erosion can occur. For the exchange of methane (CH₄) and other biogenic volatile organic compounds (BVOCs), Sect. 16.2.4.

One variable often used to address ecosystem carbon budgets is net primary production (NPP), in g C m⁻² year⁻¹, defined as GPP minus respiration (Sect. 12.​5 in Chap. 12 for leaf and plant levels and Chap. 23 for global change impacts). Thus, it includes, for example, production of fine roots, root exudation and emission of BVOVs for defence (Sect. 16.2.4). NPP constitutes about 50% of GPP (ranging from 30% to 80%) (Amthor 2000; DeLucia et al. 2007) and can be determined for above-ground and belowground tissues (ANPP and BNPP, respectively). Moreover, allometric relationships (i.e. statistical relationships used to predict tree biomass) relate BNPP to total NPP. For example, for trees BNPP/NPP = 0.3, and for grasses BNPP/NPP = 0.5. These numbers are global means and thus do not account for species differences (Sect. 22.​2 in Chap. 22). Moreover, most NPP estimates given in the literature are ANPP estimates only, neglecting below-ground production but also herbivory and other processes like exudation and BVOC emissions.

Thus, NPP should not be interpreted as yield, harvest or above-ground biomass production over time (e.g. ANPP per growing season, cropping time, year). Two examples illustrate this misconception: Farmers consider grain production as yield but are not necessarily interested in stem and root growth; foresters are mostly interested in cumulative stem growth and increase in wood volume at time of harvest but not in foliage growth or even stem mortality until harvest. Moreover, thinning and harvest residues are clearly part of NPP but not considered in assessments of net increment changes in forests. Both examples illustrate that the harvestable yield is only a small fraction of NPP.

Each method has its own uncertainties, but generally sequential coring and minirhizotron estimates seem to overestimate turnover, while radiocarbon analyses seem to underestimate turnover (Gaul et al. 2009). Consequently, estimates of mean life span for the same fine roots might differ. In temperate forests, life spans of typically <1–2 years were found based on sequential coring and minirhizotron methods. However, fine root life spans were much larger, up to 8 years (top soil) and 18 years (deeper soil horizons), based on radiocarbon analyses (Gaudinski et al. 2001). However, radiocarbon estimates can be biased, depending on which carbohydrate substrates with which age (i.e. time since bomb tests) are used for fine root production. Clear evidence was provided by Vargas et al. (2009) using radiocarbon analyses in five tropical forest stands before and after Hurricane Wilma hit. Fine roots grown into ingrowth cores installed after the hurricane were estimated to be 2–10 years old. Thus, trees had remobilised stored, that is, old, carbohydrates to supply new fine root production and did not use recently assimilated carbon. This made new roots look much older! Independently of the method used, most studies find thicker and deeper roots being older than fine roots in the top soil. Root turnover differs among different ecosystem types. For example, fine root turnover in grasslands is typically much greater than in forests, that is, the life span of fine roots in grasslands is much shorter. In comparison, leaves and needles in temperate forest ecosystems have a life span of 1–10 years (Pinus aristata even 30 years). Wood can remain at a plant >100 years (oldest living trees: 5000 years, Pinus longaeva, Bristlecone pine), while SOM is often >100–1000 years old.

One of the largest CO₂ fluxes in terrestrial ecosystems is soil respiration (also called soil CO ₂ efflux), comprising between 50 and 70% of total ecosystem respiration (Raich and Schlesinger 1992). Soil respiration includes respiratory losses from plants and plant-root-related microorganisms in the rhizosphere (Box 11.​1, Chap. 11), microbial respiration (MR) during decomposition of litter and SOM as well as respiration of soil fauna (Fig. 16.12). The strict separation into auto- and heterotrophic soil respiration is not useful since MR is intricately coupled to plant activity, particularly to canopy photosynthesis, not only in the rhizosphere via root production and exudation but also via litter production. Depending on the substrates used for respiration, turnover rates and, thus, residence times in the soil differ. While roots respire relatively young carbohydrates allocated below-ground (<1 year to several years), MR use substrates from root exudation (<1 year) or organic matter, ranging in age from leaf litter (<1 year to several years) to very old SOM (decades to millennia). Thus, the drivers of soil respiration are both biotic (carbon supply via photosynthesis and allocation below-ground) and abiotic (environmental conditions), but they also interact with each other. For example, with increasing temperature, not only respiration increases, but also photosynthesis and in turn allocation below-ground may increase up to a certain limit. With increasing N supply, productivity increases, but also the root:shoot ratio and the litter quality change, affecting MR during mineralisation of plant litter.

Overall, the most important driver of soil respiration is canopy assimilation. This can be seen when above-ground biomass is cut, for example, in managed grasslands, while abiotic conditions like soil temperature and moisture remain unchanged. Soil respiration drops within a couple of days and only resumes when above-ground biomass, and thus LAI, is regrown. Högberg et al. (2001) used stem girdling in a northern pine forest to show for the first time the strong coupling of canopy photosynthesis to below-ground respiration (Sect. 14.​2, Chap. 14). Girdling is the removal of the phloem in the bark of trees, which interrupts the supply with carbohydrates assimilated in the canopy to the root system. Depending on the starch pool in the roots, the drop in soil respiration occurred faster (low starch pool, end of season) when trees were girdled later in the year than when girdled in spring (still high starch pool, beginning of season). Similarly, drought slows down carbon allocation below-ground, affecting soil respiration negatively (Rühr et al. 2009). Thus, overall, soil respiration scales positively with GPP, NPP, LAI, litter production and carbohydrate supply below-ground. This affects both root-rhizosphere respiration (RR) and MR, which are tightly related to each other as well (Bond-Lamberty et al. 2004). Changes in phenology, co-occurring with changes in environmental conditions, thus affect soil respiration in mixed deciduous forests too (Ruehr and Buchmann 2010). During the growing season with full canopy cover, RR is greater than microbial soil respiration, contributing on average 50–60% to total soil respiration. However, during the dormant season, this contribution of RR drops to about 30%, with microbial soil respiration dominating the overall soil CO₂ flux.

Nevertheless, environmental conditions, particularly soil temperature and soil moisture, also regulate soil respiration (Sect. 13.​3, Chap. 13). Since both abiotic factors also drive canopy photosynthesis and are more readily available than GPP, soil respiration is often modelled with climatic data, particularly at large spatial scales. Soil respiration increases exponentially with soil temperature, while low soil moisture contents decrease soil respiration below this general relationship. Phenology also affects these functional relationships (Fig. 16.13). During the growing season, both RR and MR show similar relationships with soil temperature. However, during the dormant seasons, when fluxes are lower, MR reacts more strongly to increasing soil temperatures (steeper slope) than root respiration. Most likely, RR during the dormant seasons is limited by carbon substrates compared to MR, which can use many organic matter substrates available in the soil. Owing to these interacting multiple drivers, a simple Q ₁₀ value, which describes the increase of an enzymatic process when temperature is increased by 10 K, cannot capture this complexity. Thus, it should not be used to describe soil respiration fluxes in response to changing environmental drivers, not even to temperature changes alone (for further details, Davidson et al. 2006). Instead, modelling needs to take into account both environmental and biotic variables (Chaps. 15 and 22).

16.2.2 Decomposition and Stabilisation of Organic Matter in Terrestrial Ecosystems

Foliage decomposition is strongly linked to litter quality (in particularly to relative concentrations of water-soluble C compounds, cellulose, lignin and N) (Cotrufo et al. 2013) and to environmental conditions. The higher the quality, the faster the breakdown, under adequate soil moisture and temperature regimes for microbial activities (Sect. 20.​4, Chap. 20). Simple decay models describe the patterns of exponential mass loss per year (Eq. 16.16). For parameterisation of organic matter decay and SOM formation in ecosystem and global models, Sects. 15.​3 and 22.​3 in Chaps. 15 and 22, respectively:

(16.16)

with X/X _o describing the percentage mass remaining and k being the decomposition constant (year⁻¹).

Decomposition constants (also called k-values; under steady-state with 1/k = MRT, mean residence time or turnover time) for mass loss range from about 0.25 to 0.47 in Mediterranean and temperate regions vs. 2.3 in tropical areas. Thus, it takes on average 2.1–4 years vs. about 5 months to decompose foliage litter in Mediterranean and tropical climates, respectively. This first step of foliage decomposition occurs in several phases, with the dynamics for C (Fig. 16.14a) being different to those for N (Fig. 16.14b). For a newly fallen leaf (leaf litter), its C content decreases because of the use of easily decomposable C compounds (sugar, hemicellulose, cellulose) by soil fauna and soil microorganisms. At the same time, the N content rises initially, as bacteria and fungi settle on the dead leaf (for beech, this takes about 1 year). Finally, N-containing substances are decomposed, and the N content of the leaf decreases as organisms retreat from the leaf (for beech, after about 3 years). After 3 years, the leaf has lost about 80% of its mass and 60% of its N content (Cotrufo et al. 2000). Further decomposition in later phases is much slower. Lignin is then decomposed by fungi, but for this process an additional C source is required (Gleixner et al. 2001).

Decomposition of wood takes much longer than leaf or fine root decomposition, often between 50 and >100 years. Reported k-values for coarse woody debris (>10 cm in diameter) range from 0.0025 (400 years) to 0.089 (11 years). However, these very long residence times are rather exceptions. In general, mean residence times are shorter in the tropics (8–21 years) than in temperate latitudes (21–29 years) or in high latitudes (25–28 years) (Bloom et al. 2016). Mass loss rates vary strongly with wood density and wood chemistry, but also with decomposer activities linked to environmental conditions. Due to higher lignin:N ratios, the wood of gymnosperms decomposes slower than that of angiosperms, when trees grew at the same site (Weedon et al. 2009). Lignins are high-molecular-mass, three-dimensionally structured compounds of phenylpropane units that enclose cellulose fibrils. Conifers form lignin from coniferyl alcohol and deciduous trees use both coniferyl and sinapyl alcohols. Grasses also use coumaryl alcohol. Degradation occurs by laccase-forming fungi (white rots), which break bonds in side chains and aromatic rings by forming oxygen radicals (Zech and Kögel-Knabner 1994). Mass loss of wood is also related to the fire history of the site (Fig. 16.15). In boreal coniferous forests, trunks killed by fire are degraded faster than in unburnt areas. Mass loss is finished after about 120 years, with part of the dead wood being burned because of periodic ground fires.

The stabilisation of organic matter, that is, the formation and protection of SOM, has received a lot of attention over the last decade. Stabilisation is related to chemical changes of decomposition products mediated by soil fauna (e.g. earthworms that change the chemistry of the organic residue) and microorganisms, but also to physical protection, for example, by the soil matrix, by association with minerals or occlusion in soil aggregates. Both factors can reduce the chance that organic matter will be decomposed and thus lead to the persistence of organic matter in the soil over long time periods (Schmidt et al. 2011; Cotrufo et al. 2013), contributing to long-term carbon (and nutrient) storage in soils. For example, newly formed microbial polysaccharides (bacterial slime) bind to clay and silt fractions in the soil and are thereby stabilised against further decomposition. Thus, the clay content determines the ability of soils to store C (Bird et al. 2001). In stark contrast to the initial steps of decomposition, during stabilisation, the molecular structure of the organic matter or the recalcitrance of organic matter as a substrate for decomposition is only marginally important. Even “easily decomposable” sugars can persist in the soil for decades when protected (or immobilised in constantly active microbial biomass), and even “recalcitrant” lignin and plant waxes can be decomposed at rates higher than the bulk soil when conditions are right. Similarly, the relevance of humic substances as very stable SOM fractions, formed de novo during decomposition, needs to be revisited. Inferred from the classical extraction methods in soil chemistry, the amount and relevance of humic substances have been largely overestimated. Their new formation is no longer considered quantitatively relevant for humus formation in soils. Nevertheless, most soil carbon models still use the structure and inferred decomposability of organic matter to drive their decomposition models (Chaps. 15 and 22). Instead, fire-derived organic matter has been identified as being highly relevant and can make up to 40% of total SOM in many forest and grassland soils (Box 16.2). Deep soil layers are still a black box, although globally they store more than 50% of total soil carbon pools.

Box 16.2: Black Carbon and Terra Preta Soils

A highly recalcitrant form of soil carbon, which is very difficult to degrade, is charcoal or black carbon. When organic matter is combusted under limited oxygen supply (charred), char, charcoal or soot (which can be distinguished by the molecular ratios of oxygen to carbon and hydrogen to carbon) is produced, forming condensed aromatic and carboxylic structures similar to graphite (Fig. 16.16a) (Gleixner et al. 2001; Glaser 2007). These structures are highly stable against microbial decomposition (but can be decomposed eventually).

In the central Amazon, “islands” with highly fertile soils, called terra preta, have been recorded, surrounded by very infertile soils, often ferralsols (Fig. 16.16b, c). These fertile soils contain about 3 times the amount of SOM, about 70 times more charcoal, higher nutrient content and a better nutrient retention capacity than their surrounding soils (Glaser 2007). These soils were formed in pre-Colombian times, about 7000 to 500 years BP, and have been used for agriculture ever since, so they are considered anthropogenic soils. The origin of the black carbon (also called biochar) is not entirely clear, but natural forest fires do not sufficiently explain the high black carbon content. Anthropogenic activities such as low-heat smouldering fires as used for cooking or spiritual uses have been proposed as source for the biochar. Higher microbial activities are found in terra preta soils as well as after charcoal additions to infertile ferralsols, probably due to the porous structure of charcoal, providing habitats for soil microorganisms. In addition, biochar is electrically conductive, so it can affect electron transfer processes by functioning as an electron shuttle, increasing, for example, N₂ fixation by free-living prokaryotes (Kappler et al. 2014). After the original combustion product has been oxidised on the edges by microorganisms in the soil (Glaser et al. 2002), black carbon also adds a cation exchange capacity to soils and, thus, a high nutrient retention capacity. Currently, the application of charcoal for sustainable agriculture is recommended.

16.2.3 Net Ecosystem Production and Net Biome Production

Integrating over all assimilatory and respiratory processes taking place at the same time in a terrestrial ecosystem becomes necessary if one is interested in the response of ecosystems to management or climate or if one wants to compare flux magnitudes across ecosystem types. Measuring all processes separately and scaling them up to the ecosystem level is impossible and would introduce a huge uncertainty into the final flux estimate (Sect. 14.​1, Chap. 14). Thus, one uses a micrometeorological approach (eddy covariance method, Box 16.1) to directly measure net carbon dioxide fluxes between the ecosystem and the atmosphere, that is, the net ecosystem CO ₂ exchange (NEE) (in μmol CO₂ m⁻² s⁻¹). NEE data are typically given using the meteorological sign convention (from an atmospheric perspective): negative values represent situations where the atmosphere loses CO₂ while the ecosystem takes up CO₂ and acts as carbon sink; positive values represent situations where the atmosphere gains CO₂ while the ecosystem loses CO₂ and acts as a carbon source. NEE is measured continuously over long time periods at high temporal resolution, typically at 10–20 Hz (10–20 times per second). The longest time series reaches back to 1992 (Harvard Forest, USA), and today data from >850 flux tower sites are available globally (Sect. 14.​1, Chap. 14). Summing up NEE (generally aggregated to 30 min averages) to annual values results in net ecosystem production NEP (typically in g C m⁻² year⁻¹), which is given as a positive number to represent a carbon sink (in contrast to NEE!). NEP is the small net difference between two large fluxes, GPP and all auto- and heterotrophic respiratory losses (Eq. 16.17), and can be approximated by NPP minus heterotrophic respiration. When no additional C inputs such as fertilisation and no additional C exports such as harvests, fire or erosion occur, NEP represents the ecosystem carbon budget, that is, the ecosystem C sink or source. However, when additional inputs and exports occur, these C fluxes need to be taken into account when calculating the ecosystem carbon budget. Then the C budget is called net biome production (NBP) (Eq. 16.18) (Schulze et al. 2000), even if a field or ecosystem type (and not a biome) is studied:

(16.17)

(16.18)

where R _a is the respiration of autotrophic plants, R _h the respiration of heterotrophic organisms, and R _e the total ecosystem respiration, with R _e = R _a + R _h. Exports are additional C losses and can be harvests, C emitted as BVOCs, fire or erosion. Inputs are additional C sources such as organic fertilisers, that is, slurry and manure.

Most of the carbon enters the ecosystem as CO₂ via GPP (except organic fertilisation; see subsequent discussion). About 50% of GPP is used for NPP (Fig. 16.17). The NPP/GPP ratio, also called carbon use efficiency, varies with vegetation type and responds to changes in environmental conditions. Median values of NPP/GPP, considering ANPP and BNPP, range from about 0.3 for boreal forests, to 0.4 for temperate coniferous, 0.5 for tropical forests and 0.55 for temperate deciduous forests (DeLucia et al. 2007). Using remote sensing, the ANPP/GPP ratios can be estimated (Zhao et al. 2005), resulting in values between 0.35 and 0.54 for forests, 0.58 for cropland and 0.65 for grasslands, validated by inventories and flux measurements.

To know when an ecosystem is a carbon sink or a source, the net balance between gross photosynthesis and ecosystem respiration needs to be known. The diurnal courses of NEE clearly show when a particular process dominates. During the night, only respiration occurs. During the day, photosynthesis can be compensated by respiration (often the case in winter) or photosynthesis can overcompensate respiration (during most of the growing season). Thus, depending on the time of day and the day of the year, the ecosystem acts as either a CO₂ source (nighttime, winter) or a CO₂ sink (daytime, growing seasons). This general pattern occurs throughout the year, but environmental conditions, phenology and management determine the relationship of CO₂ loss to uptake and, thus, the daily NEE flux.

The NEE of an intensively managed temperate grassland shows photosynthetic activities already in spring and highest uptake during summer (green and blue colours in Fig. 16.18a) (Zeeman et al. 2010). Therefore, sink activities start as early as February/March if the winter is mild (as in winter 2006/2007) but can also be delayed until April/May (as in winter 2005/2006). During the main growing season (May to September), high CO₂ uptake rates are measured during the day and only interrupted by management interventions, that is, frequent cuts of the meadow and subsequent manure applications. Then photosynthesis drops to very low rates and respiration dominates, both from the soil and the manure (orange and red colours in Fig. 16.18a). Presenting the cumulative NEE fluxes (Fig. 16.18b) reveals a typical zigzag pattern over the course of the growing season. When the grassland has grown well (NEE very negative, indicating high CO₂ uptake; data at the lowest point in a zigzag pattern), the farmer will cut the meadow to harvest the biomass and subsequently apply manure to fertilise the vegetation. Thus, after the harvest, photosynthesis is small and soil respiration dominates NEE for some days (NEE becomes less negative; data on the upward-pointing leg of a zigzag). When the regenerating vegetation carries out enough photosynthesis to overcompensate soil respiration, NEE will become more negative again (data on the downward-pointing leg of a zigzag). This zigzag pattern will repeat itself with each combined cut-and-manure event. At the end of the year, this grassland shows a carbon balance between assimilation and respiration of about 90 g C m⁻² year⁻¹ (Fig. 16.18b). However, this balance is not yet the ecosystem carbon budget since the grassland was harvested multiple times (C exports) and received large amounts of organic fertiliser (C inputs). Accounting for the carbon in these additional exports (about 350 g C m⁻² year⁻¹) and inputs (about 330 g C m⁻² year⁻¹), the NBP and, thus, the ecosystem carbon sink was about 70 g C m⁻² year⁻¹.

If an ecosystem does not experience additional exports and inputs during the year (e.g. by management or DOC fluxes), the final value of the cumulative NEE curve gives an estimate of the ecosystem carbon sink. This is often the case in forests, which are not managed on an annual basis. Evergreen forests can exhibit small sink activities also over winter, while sink activities in deciduous forests start with the leaf-out of the understorey vegetation (e.g. Allium ursinum, wild garlic, in temperate beech forests) and show peak NEE fluxes when the tree canopy is fully developed. Thus, phenology is an important driver of NEE and NEP. The longer the growing season, the higher the NEP: deciduous broadleaf forests increase their NEP by 5.6–5.8 g C m⁻² per day of the growing season, evergreen needle-leaf forests by 3.4 g C m⁻² day⁻¹, savannas by 3.7 g C m⁻² day⁻¹ and grasslands and croplands by 7.9 C m⁻² day⁻¹ (Churkina et al. 2005). Climate variables have large effects on NEE, but also on GPP and R _e. Both component fluxes depend primarily on light but increase with temperature and precipitation until limitations set in (heat or freezing stress, drought). This is true not only of the current year’s weather but also of the previous year’s weather, since carbon allocation and storage drive bud establishment and growth the following year. Furthermore, disturbances, either slow or sudden, affect ecosystem CO₂ fluxes. N deposition was shown to increase the NEP. Fire frequency and intensity affect both GPP and R _e. Drought and heatwaves affect GPP more negatively than R _e, shifting ecosystem NEE towards respiratory losses and even releasing CO₂ from SOM, sometimes worth several years of C sequestration (Ciais et al. 2005). Old forests still sequester carbon (Sect. 14.​1, Chap. 14), although sometimes at lower rates than mature forests. For further examples, please see Baldocchi (2008, 2014).

Stable carbon isotopes as well as radiocarbon (Sect. 16.2.1) data provide further insights into the carbon turnover and the fate of carbon within an ecosystem. The source of carbon dioxide for plant photosynthesis is atmospheric CO₂, which currently has a δ¹³C value of about −8.3‰ (declining due to fossil fuel burning; Sect. 23.​3 in Chap. 23). Within the canopy, atmospheric CO₂ is mixed with respired CO₂, which has a δ¹³C value close to the organic substrate being respired (between −30 and −18‰ for C₃ plants), resulting in canopy δ¹³C profiles between the atmospheric background at the top of the canopy (Fig. 16.19) and a mix of both CO₂ sources close to the ground (reaching values of around −14 to −16‰). δ¹³C gradients in canopy CO₂ vary with time of day, being small during the day when turbulent mixing occurs within the canopy and large at night under stable atmospheric conditions. This canopy CO₂ with its δ¹³C is then the source for photosynthesis. Discrimination against ¹³CO₂ happens during CO₂ diffusion into foliage as well as during CO₂ fixation (and respiration) (for detailed reviews see Ghashghaie and Badeck 2014 and Werner and Gessler 2011). Thus, depending on where the foliage is located within a canopy, not only the ecophysiology of foliage but also the source δ¹³C determines the foliar δ¹³C values in any ecosystem. As a result, foliage in the top canopy has higher δ¹³C values than foliage closer to the ground (Fig. 16.19). In general, 30% of the gradients in foliar δ¹³C are due to canopy CO₂, about 70% to ecophysiology (Buchmann et al. 2002). If foliage senesces and becomes litter and SOM, δ¹³C values increase owing to fractionation during mineralisation and processes related to decomposition. Similarly, soil-respired CO₂ has a higher δ¹³C than SOM. For further details, please refer to Brüggemann et al. (2011).

Moreover, the δ¹³C in foliage integrates over the entire lifespan of a leaf, while δ¹³C litter integrates over all species currently present in an ecosystem. In turn, δ¹³C of SOM integrates over current and past vegetation. This is particularly interesting when vegetation had changed from C ₃ to C ₄ vegetation or vice versa, since carbon isotope discrimination differs strongly between these two photosynthesis types (Sect. 12.​2, Chap. 12). Thus, δ¹³C of SOM within a soil profile can give information about the dominant vegetation, forest or (C₄) grassland, over time, particularly when the age of SOM is known. The difference between the δ¹³C of atmospheric CO₂ entering the ecosystem for GPP and the δ¹³C of respired CO₂ of ecosystems, the so-called isotopic disequilibrium, is an important piece of information for global inverse atmospheric models that are used to estimate global sinks and sources.

16.2.4 Fluxes of CH₄ and Other Biogenic Volatile Organic Compounds

Although CO₂ dominates the discussion about the carbon dynamics of ecosystems, CO₂ is not the only carbon-containing gas being exchanged between ecosystems and the atmosphere: the exchange of methane (CH₄) and other BVOCs are highly relevant for many ecosystems as well.

Biogenic methane is produced by bacteria (Archaea; methanogenic bacteria) in anaerobic zones in soils and is a potent greenhouse gas (Fig. 16.20) (Chap. 23). The highest CH₄ production is thus found in wet or waterlogged soils, for example, in rice paddies and wetlands. However, between 60 and 90% of the CH₄ produced is oxidised to CO₂ by methanotrophs, that is, bacteria widespread in soils, representing a large sink for CH₄, which is relevant for global change (Le Mer and Roger 2001). CH₄ emissions from soils to the atmosphere can happen via diffusion or as bubbles from wetland soils (called ebullition), but also via vascular plants. Here, the aerenchyma of wetland plants (such as Carex species or Eriophorum vaginatum) acts like a chimney for CH₄, bypassing potential oxidation in the upper soil layers, thereby increasing CH ₄ emissions from these ecosystems. The aerenchyma of aquatic or wetland plants (mainly in herbaceous plants but also in Alnus) is a modified parenchyma tissue with large cavities formed under anoxic conditions to mediate gas exchange (mainly of oxygen) between shoots and roots. Outgassing of CH₄ via aerenchyma tissues can be responsible for up to 90% of the CH₄ emissions during the growing season. The chimney effect increases with higher soil carbon contents, is higher under convective than under stable atmospheric conditions, and has been reported to scale with stomatal conductance (Joabsson et al. 1999; Le Mer and Roger 2001).

Plants emit a wide range of BVOCs such as isoprene (C₅H₈) and methanol (CH₃OH), the two most abundant BVOCs after CH₄ (Guenther et al. 2012), but up to 1700 substances have been reported (Loreto and Schnitzler 2010). Plants use BVOCs to communicate with each other, but also with other organisms, for example, as a wound signal (Sect. 19.​3 in Chap. 19), and constitute up to 2–5% of the net carbon gain of heavily emitting broadleaf trees (e.g. Eucalyptus, Quercus and Populus). But BVOCs have also been found to relieve oxidative and thermal stresses. Two environmental factors typically increase foliar BVOC emissions, temperature and light, while water stress does not show an effect. While many of these flux measurements were made using small leaf enclosures (Guenther et al. 2012), such fluxes have also been measured at the ecosystem level using micrometeorological techniques (Sect. 14.​1 in Chap. 14) (Wohlfahrt et al. 2015). Although these measurements supported environmental and biological controls, they also provided clear new evidence that, for example, ethanol fluxes are bi-directional: into and out of terrestrial ecosystems. In addition, land-use practices, such as clearing of understorey vegetation in forests or cutting of meadows with subsequent manure application, increased methanol emissions significantly over a couple of days (Fig. 16.21). Under a future climate, BVOC emissions are expected to increase owing to global warming, with large effects on atmospheric chemistry (Peñuelas and Staudt 2010).